1.5梯形（共2课时）

1.5 梯形（第1课时）
学习目标：
1、知道梯形、等腰梯形、直角梯形的有关概念；能说出并证明等腰梯形的性质。
2、会运用梯形的有关概念和性质进行有关问题的论证和计算。
3、通过添加辅助线，把梯形的问题转化成平行四边形或三角形问题，体会图形变换的方法和转化的思想。
学习重点：探索等腰梯形特征.
学习难点：运用轴对称性和转化的思想研究等腰梯形的特征.
学习过程
一、情景导入，目标定向
列举生活中梯形的实例，例如： 等，都给我们以梯形的形象。梯形特别是等腰梯形具有怎样的性质呢？
二、学案引领，自主学习
阅读教材p28-29，完成下面的问题：
1、一组对边 ，另一组对边 的四边形叫做梯形。 的两边叫做梯形的底，不平行的两边叫梯形的 ，在两底之间，与底垂直的线段叫做梯形的 。两腰相等的梯形叫 一腰与底垂直的梯形叫 。
三、合作探究，交流展示
1、等腰梯形是轴对称图形吗？如果是它有几条对称轴？取一张等腰梯形的纸片，折一折，试一试。
2、根据等腰梯形的轴对称性，你发现同一底上的两个内角的大小具有怎样的关系？
3、证明你的结论：如图，梯形ABCD中，AD∥BC，AB=CD，求证∠B=∠C，∠A=∠ADC。
4、度量等腰梯形ABCD的两条对角线的长，你有什么发现？根据等腰梯形的性质定理1和全等知识你能证明吗？
四、启发引导，精讲点拨
如图，在等腰梯形ABCD中，AD∥BC，∠B＝60°，AD＝15，AB＝20，求BC的长。
还有其他添加辅助线的方法吗？
五、系列训练，当堂达标
1、梯形上底长为5cm，过上底的一个端点引一腰的平行线与下底相交，若所得三角形周长为20cm，则梯形周长等于___________cm。
2、在梯形ABCD中，AD∥BC，若∠B=500，∠C=800，则∠D= ，∠A= .
3、已知等腰梯形有一角为1200，腰长为3cm，上底长为4cm，则下底长为 .
4、等腰梯形的一个锐角为60°,一腰长为24cm,一底长为39cm,则另一底长为 .
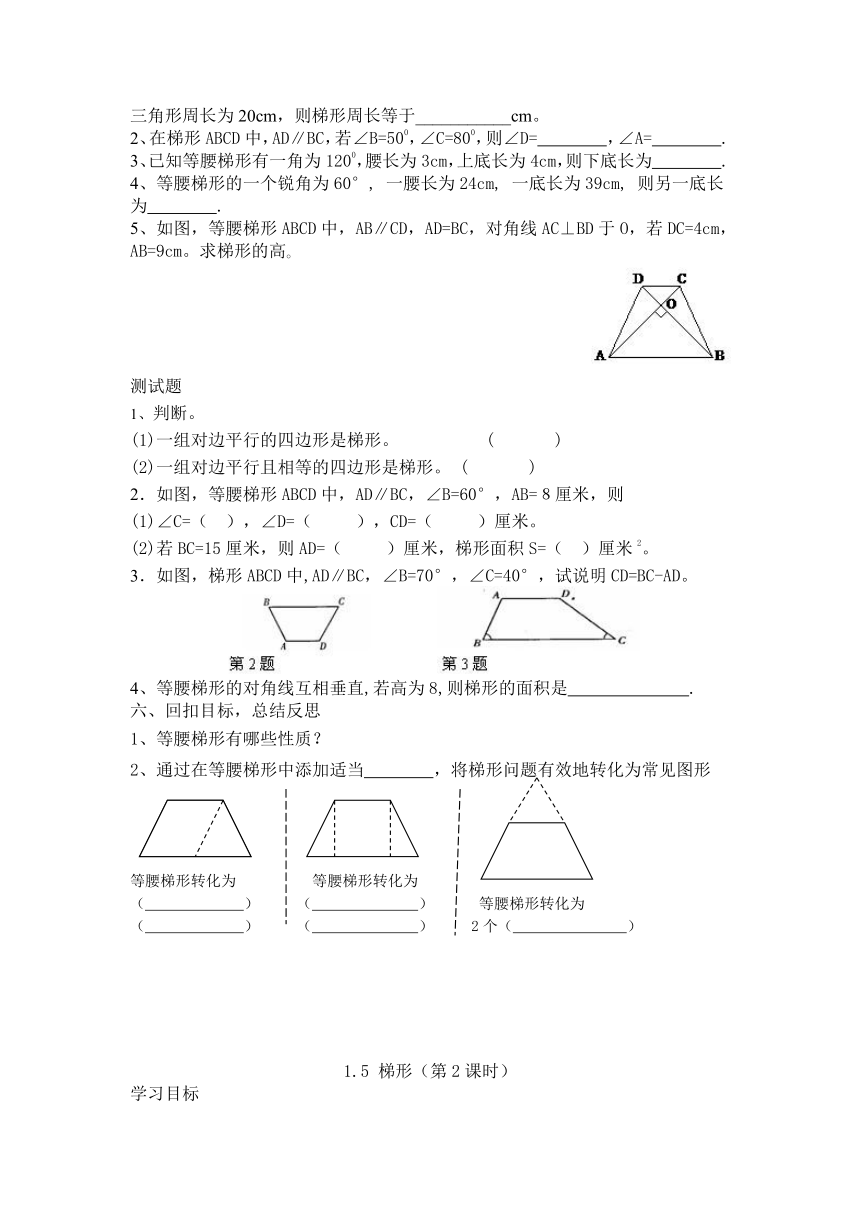
5、如图，等腰梯形ABCD中，AB∥CD，AD=BC，对角线AC⊥BD于O，若DC=4cm，AB=9cm。求梯形的高
测试题
1、判断。
(1)一组对边平行的四边形是梯形。 ( )
(2)一组对边平行且相等的四边形是梯形。 ( )
2．如图，等腰梯形ABCD中，AD∥BC，∠B=60°，AB=８厘米，则
(1)∠C=（ ），∠D=（ ），CD=（ ）厘米。
(2)若BC=15厘米，则AD=（ ）厘米，梯形面积S=（ ）厘米2。
3．如图，梯形ABCD中,AD∥BC，∠B=70°，∠C=40°，试说明CD=BC-AD。
4、等腰梯形的对角线互相垂直,若高为8,则梯形的面积是 .
六、回扣目标，总结反思
1、等腰梯形有哪些性质？
2、通过在等腰梯形中添加适当 ，将梯形问题有效地转化为常见图形
等腰梯形转化为 等腰梯形转化为
（ ） （ ） 等腰梯形转化为
（ ） （ ） 2个（ ）
1.5 梯形（第2课时）
学习目标
1、认识梯形的定义并掌握梯形的相关判定并能证明等腰梯形的判定定理。
2、熟练应用的等腰梯形的判定定理.
学习重点：等腰梯形的判定。
学习难点：解决梯形问题的基本方法（将梯形转化为平行四边形和三角形）
学习过程
一、情景导入，目标定向
1、 是等腰梯形。
2、等腰梯形具有哪些性质？
性质1：
性质2：
二、学案引领，自主学习
1．你能说出等腰梯形性质定理1的逆命题吗？
2．你能证明这个逆命题是真命题吗？
已知：
求证：
证明：
等腰梯形的判定定理：
三、合作探究，交流展示
如图，在梯形ABCD中，AD∥BC，AC=DB，求证：梯形ABCD是等腰梯形。
通过证明我们可以得到等腰梯形的另一个判定定理： 。
四、启发引导，精讲点拨
如图梯形ABCD中，AD∥BC，M是AD的中点，∠MBC=∠MCB求证：四边形ABCD是等腰梯形；
五、系列训练，当堂达标
1、下列说法：①对角线相等的梯形是等腰梯形，②对角线互相垂直的矩形是正方形，其中正确的是（ ）
A、①正确②不正确 B、①②都正确 C、①②都不正确 D、①不正确，②正确
2、用两个全等的直角三角形一定能拼出的图形是 （ ）
A 等腰梯形 B 直角梯形 C 菱形 D 矩形
3、一组 对边平行，并且对角线互相垂直且相等的四边形是 （ ）
A、菱形或矩形 B、正方形或等腰梯形 C、矩形或等腰梯形 D、菱形或直角梯形
4、如图，在ABCD中，E是BC的中点，且∠AEC＝∠DCE，则下列结论不正确的是（ ）
A、BF＝DF B、S△AFD＝3S△EFB
C、四边形AECD是等腰梯形 D、∠AEB＝∠ADC
5、如图，在梯形ABCD中，AD∥BC，∠A，∠C互补，梯形ABCD是等腰梯形吗？
测试题
1、四边形的四个内角的度数比是2∶3∶3∶4，则这个四边形是（ ）
A.等腰梯形 B.直角梯形 C.平行四边形 D.不能确定
2、如图，在等腰梯形ABCD中，AD∥BC，对角线AC、BD相交于点O，下列结论不一定正确的是（　　）
A．AC=BD B．OB=OC C．∠BCD=∠BDC D．∠ABD=∠ACD
（2、3题图） （4题图）
3、在梯形ABCD中，AD∥BC，对角线AC和BD交于点O，下列条件中，能判断梯形ABCD是等腰梯形的是（　　）
A、∠BDC=∠BCD B、∠ABC=∠DAB C、∠ADB=∠DAC D、∠AOB=∠BOC
4、如图，梯形ABCD中，AD∥BC，AB∥DE，∠DEC=∠C，求证：梯形ABCD是等腰梯形．
六、回扣目标，总结反思
1、我们今天学习了等腰梯形的哪几种判定？请说出来。
2、在研究梯形问题时用了哪些方法将梯形问题转化为其他图形的问题？