1.6中位线定理（共3课时）

1.6 中位线定理（第1课时）
学习目标
1、能识别三角形的中位线，能证明三角形中位线定理。
2、能用三角形中位线定理解决其它相关问题。
3、在自主探索与合作交流中，经过猜想、验证过程,进一步发展推理论证能力。
学习难点：三角形中位线定理的证明及应用。
学习过程
一、情境导入，目标定向
如图，小明家A和学校B之间有一个池塘。在没有任何工具的前提下，小明通过下面的方法估测出A、B间的距离：先在AB外选一点C，然后步测出AC、BC的中点M、N，并测出MN的长，由此他就知道了A、B间的距离。你能说说其中的道理吗
二、学案引领，自主学习
1、任意画△ABC，设AB、AC的中点分别为D，E，连接DE。得到的线段我们叫做 .这样的线段能画几条？请在（2）（3）的图中画出来。
(1) （2） （3）
2、在上图（1）中，分别量出∠ADE与∠B的大小，你发现DE与BC有怎样的位置关系？分别量出DE与BC的长，你发现DE与BC有怎样的数量关系？（2）（3）中的中位线与第三边怎样的数量关系？
于是我们得到：三角形的中位线 第三边，并且等于第三边的 。
三、合作探究，交流展示
如何证明上面的定理呢？
已知，如图，在△ABC中，点D、E分别是AB与AC边的中点。
求证：DE∥BC，DE=BC。
四、启发引导，精讲点拨
例1: 如图,顺次连接四边形ABCD各边中点E、F、G、H,得四边形EFGH，求证: 四边形EFGH是平行四边形.
五、系列训练，当堂达标
1、如图,DE是△ABC的中位线，DE=2，AB+AC=12，则梯形BCED的周长为（ ）
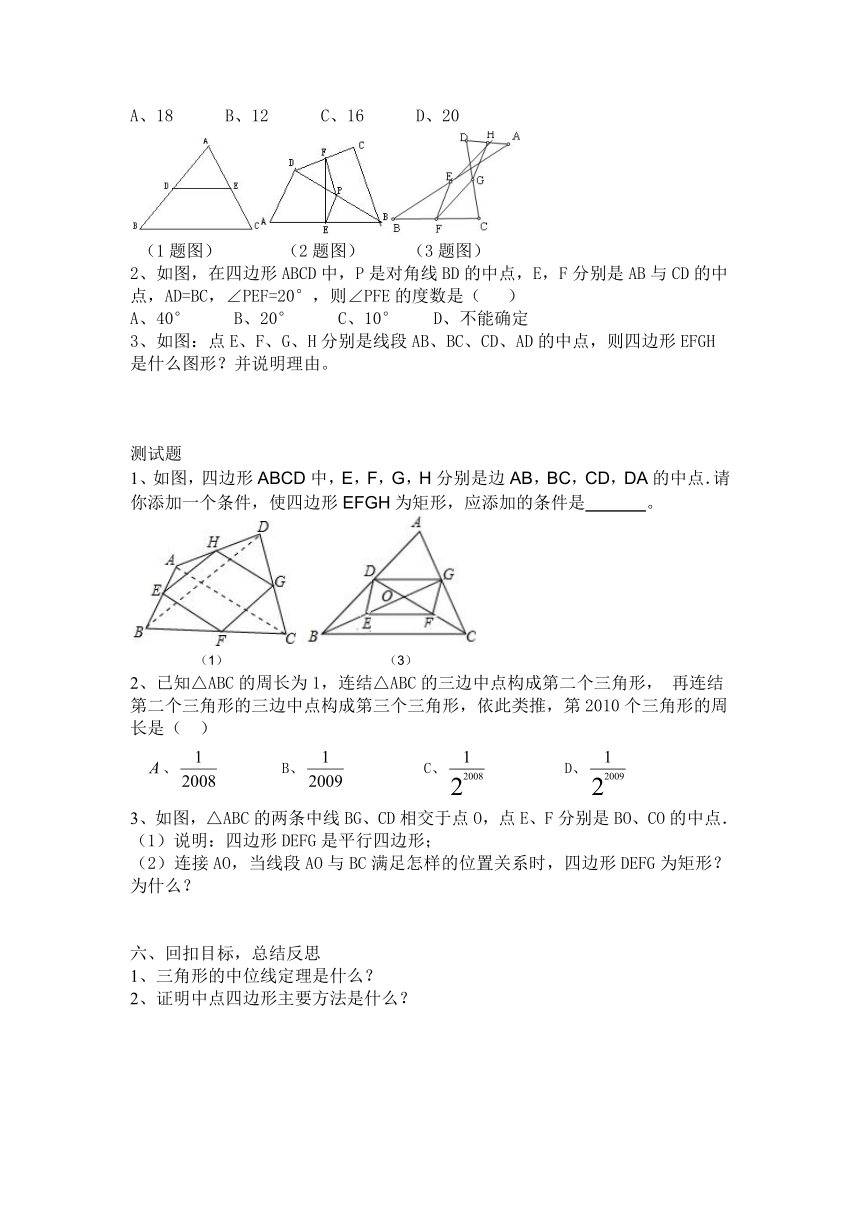
A、18 B、12 C、16 D、20
（1题图） （2题图） （3题图）
2、如图，在四边形ABCD中，P是对角线BD的中点，E，F分别是AB与CD的中点，AD=BC，∠PEF=20°，则∠PFE的度数是（ ）
A、40° B、20° C、10° D、不能确定
3、如图：点E、F、G、H分别是线段AB、BC、CD、AD的中点，则四边形EFGH是什么图形？并说明理由。
测试题
1、如图，四边形ABCD中，E，F，G，H分别是边AB，BC，CD，DA的中点．请你添加一个条件，使四边形EFGH为矩形，应添加的条件是 。

（1） （3）
2、已知△ABC的周长为1，连结△ABC的三边中点构成第二个三角形，再连结第二个三角形的三边中点构成第三个三角形，依此类推，第2010个三角形的周长是（ ）
、 B、 C、 D、
3、如图，△ABC的两条中线BG、CD相交于点O，点E、F分别是BO、CO的中点．
（1）说明：四边形DEFG是平行四边形；
（2）连接AO，当线段AO与BC满足怎样的位置关系时，四边形DEFG为矩形？为什么？
六、回扣目标，总结反思
1、三角形的中位线定理是什么？
2、证明中点四边形主要方法是什么？
1.6 中位线定理（第2课时）
学习目标
1、学生能利用三角形中位线定理判断中点四边形的形状；
2、感受中点四边形的形状取决于原四边形的两条对角线的位置与长短；
3、通过图形变换使学生掌握简单添加辅助线的方法。
学习难点：中点四边形的形状判定
学习过程
一、情景导入，目标定向
顺次连接一个四边形四边中点所得四边形称为这个四边形的中点四边形，中点四边形可以是平行四边形、矩形、菱形、正方形，那么原四边形具有什么条件呢？
二、学案引领，自主学习
通过前面的学习我们知道，连接任意四边形得到的中点四边形至少是平行四边形，那么平行四边形的中点四边形是_____________；
矩形的中点四边形是_____________；菱形的中点四边形是________________；
正方形的中点四边形是___________；梯形的中点四边形是_____________；
直角梯形的中点四边形是_________；等腰梯形的中点四边形是_________。
三、合作探究，交流展示
结合手中准备的图片，小组探究以下几个问题答案：
1、中点四边形的形状与原四边形的什么有密切关系？
2、要使中点四边形是菱形，原四边形一定要是矩形吗？
3、要使中点四边形是矩形，原四边形一定要是菱形吗？
结论：
1、中点四边形的形状与原四边形的 有密切关系；
2、只要原四边形的两条对角线_ _，就能使中点四边形是菱形；
3、只要原四边形的两条对角线 ，就能使中点四边形是矩形；
4、要使中点四边形是正方形，原四边形要符合的条件是 。
四、启发引导，精讲点拨
已知△ABC中，AB=AC，点O在△ABC的内部，∠BOC=90°，OB=OC，D、E、F、G分别是AB、OB、OC、AC的中点．
（1）求证：四边形DEFG是矩形；
（2）若DE=2，EF=3，求△ABC的面积．
五、系列训练，当堂达标
1、顺次连接等腰梯形的各边中点所成的四边形是______________。
2、如图，任意四边形ABCD各边中点分别是E、F、G、H，若对角线AC、BD的长都为20cm，则四边形EFGH的周长是（ ）。
A．80cm B．40cm C．20cm D．10cm
（2） （3） （测试3题图）
3、O是ΔABC所在平面内一动点，连接OB，OC，并将AB，OB，OC，AC的中点D，E，F，G依次连接，如果DEFG能构成四边形：
（1）如图，当O点在ΔABC内部时，证明四边形DEFG是平行四边形。
（2）当O点移动到ΔABC外部时，（1）的结论是否还成立？画出图形并说明理由。
（3）若四边形DEFG为矩形，O点所在位置应满足什么条件？试说明理由。
测试题
1、（2004 泰安）顺次连接四边形ABCD各边中点得四边形EFGH，要使四边形EFGH是矩形，可以添加的一个条件是（　　）
A．AD∥BC B．AC=BD C．AC⊥BD D．AD=AB
2、（2013 潍坊）已知四边形ABCD，对角线AC与BD互相垂直．顺次连接其四条边的中点，得到新四边形的形状一定是（　　）
A．梯形 B．矩形 C．菱形 D．正方形
3、（2013 珠海）如图，正方形ABCD的边长为1，顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1，由顺次连接正方形A1B1C1D1四边的中点得到第二个正方形A2B2C2D2…，以此类推，则第六个正方形A6B6C6D6周长是 。
4、如图，在梯形ABCD中，AD∥BC，若E，F，G，H分别是梯形ABCD各边AB、BC、CD、DA的中点．
（1）求证：四边形EFGH是平行四边形；
（2）当梯形ABCD满足什么条件时，四边形EFGH是菱形？请说明理由．
（3）四边形EFGH可能是正方形吗？若可能，请直接写出此时梯形应满足的条件；若不能，请说明理由．
六、回扣目标，总结反思
中点四边形的特殊性取决于原四边形的什么？
1.6中位线定理—梯形的中位线（第3课时）
学习目标
1、通过自主探究，类比三角形中位线的概念，得到梯形中位线概念。
2、通过探索得到有关梯形中位线的猜想，并进一步验证，掌握梯形中位线定理。
3、通过有梯度的巩固练习，学习使用梯形中位线定理,能正确运用梯形中位线定理进行计算和证明。
学习过程
一、情景导入，目标定向
1、什么是三角形中位线？三角形中位线定理的内容是什么？
2、你会计算梯形的面积吗？你能说出计算梯形面积的公式吗？
二、学案引领，自主学习
1、定义
梯形也有中位线，类比三角形中位线定义，你能给出梯形的中位线的定义吗？
任意画一个梯形ABCD，你能画出它的一条中位线吗？它有几条中位线？
2、猜想
梯形的中位线与两底有什么关系？（友情提示：包括位置关系和数量关系）如何验证你的猜想。
三、合作探究，交流展示
①量一量
任意画梯形 ABCD，如图1,设AB、CD边的中点分别为E，F，连接EF，分别度量∠AEF与∠B的大小，你发现EF与BC有怎样的位置关系？分别量出线段EF与AD、BC的长，你发现EF与AD、BC之间有怎样的数量关系？
②证一证：
已知：如图，在梯形ABCD中，点E、F分别 是AD与BC 边的中点，
求证：EF∥BC， EF=（AD+BC）
得到的结论： 。
四、启发引导，精讲点拨
1、如果梯形的中位线长为m，它的高为h，你能用m ，h表示梯形的面积S吗？
由此你能得到的新的梯形面积公式吗？
2、等腰梯形的一个底角为45°，高为h，中位线的长为m，求梯形上底的长。
五、系列训练，当堂达标
1、如图，在梯形ABCD中，AD∥BC，点E、F分别是AB、CD的中点且EF=6，则AD+BC的值是（　　）
A．9 B．10.5 C．12 D．15
（1） （2） （3）
2、如图，在梯形ABCD中，AD∥BC，E、F分别是AB、CD的中点，则下列结论：①EF∥AD；②S△ABO=S△DCO；③△OGH是等腰三角形；④BG=DG；⑤EG=HF．其中正确的个数是（　　）
A．1个 B．2个 C．3个 D．4个?
3、如图所示，在梯形ABCD中，AD∥BC，对角线AC⊥BD，且AC=12，BD=5，则这个梯形中位线的长等于 。
测试题
1、如图，梯形ABCD中，AD∥BC，E、F分别是两腰的中点，且AD=5，BC=7，则EF的长为（　　）
A．6 B．7 C．8 D．9
（1） （3）
2、若梯形的面积为8cm2，高为2cm，则此梯形的中位线长是（　　）
A．2cm B．4cm C．6cm D．8cm
3、如图在梯形ABCD中，两对角线AC、BD互相垂直于O点，且AC=6、BD=8，试求梯形ABCD的中位线MN及高h的长．
六、回扣目标，总结反思
通过本节课的学习，你对中位线定理有了哪些进一步的认识，还有哪些困惑？在本节课的学习中，用到了哪种重要的数学思想方法？