物理人教版(2019)必修第二册6.4 生活中的圆周运动 课件(共28张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册6.4 生活中的圆周运动 课件(共28张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 34.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-12-19 16:46:15 | ||
图片预览




文档简介
(共28张PPT)
第六章 圆周运动
第4节 生活中的圆周运动(1)
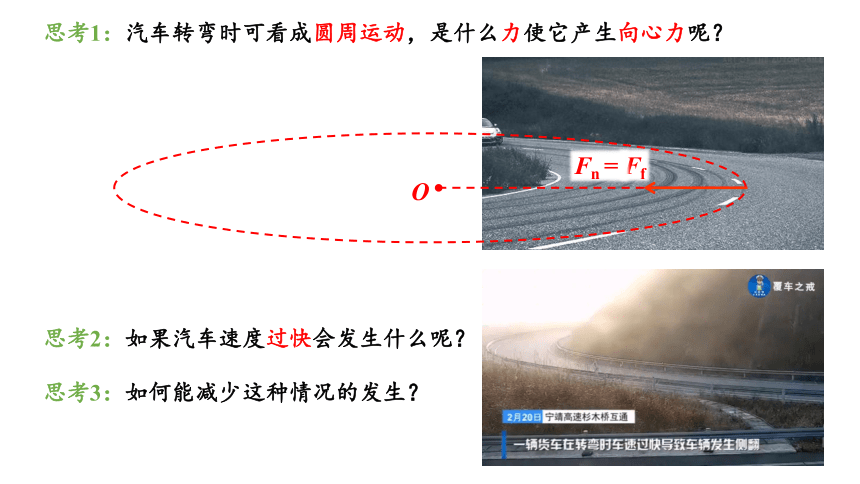
思考1:汽车转弯时可看成圆周运动,是什么力使它产生向心力呢?
O
思考2:如果汽车速度过快会发生什么呢?
Ff
Fn =
思考3:如何能减少这种情况的发生?
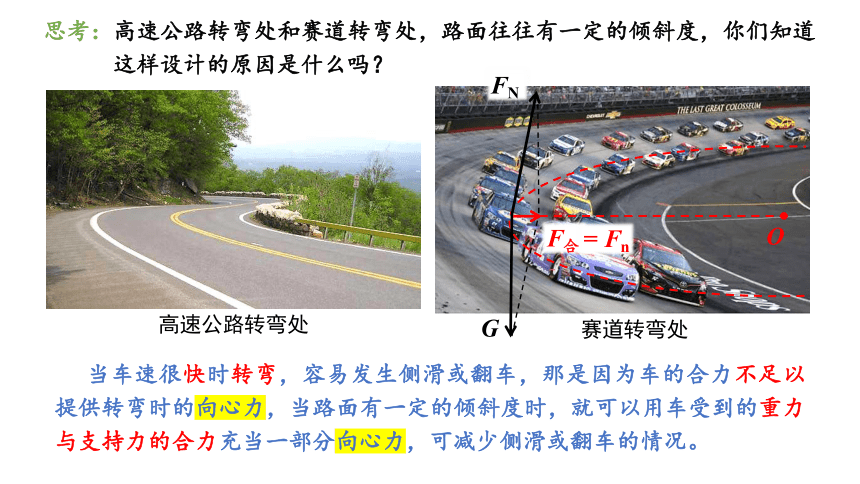
思考:高速公路转弯处和赛道转弯处,路面往往有一定的倾斜度,你们知道
这样设计的原因是什么吗?
赛道转弯处
高速公路转弯处
F合
当车速很快时转弯,容易发生侧滑或翻车,那是因为车的合力不足以提供转弯时的向心力,当路面有一定的倾斜度时,就可以用车受到的重力与支持力的合力充当一部分向心力,可减少侧滑或翻车的情况。
O
= Fn
FN
G
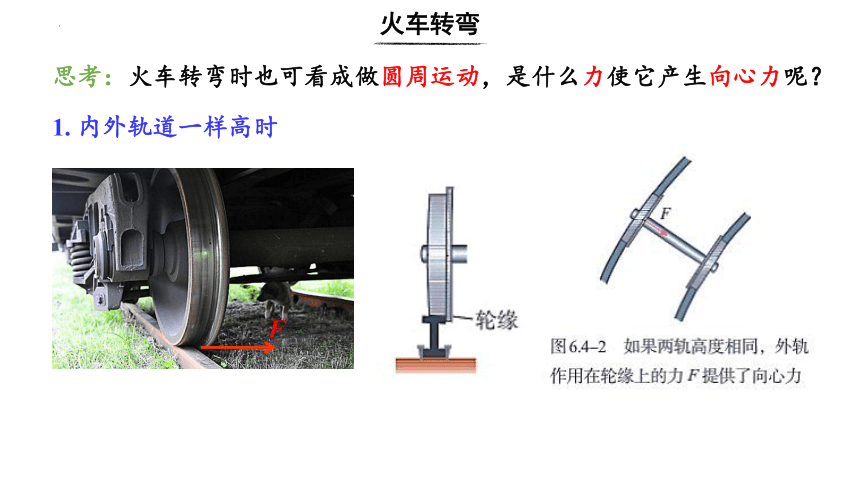
1. 内外轨道一样高时
F
火车转弯
思考:火车转弯时也可看成做圆周运动,是什么力使它产生向心力呢?
我是铁路设计师
(
θ
外
内
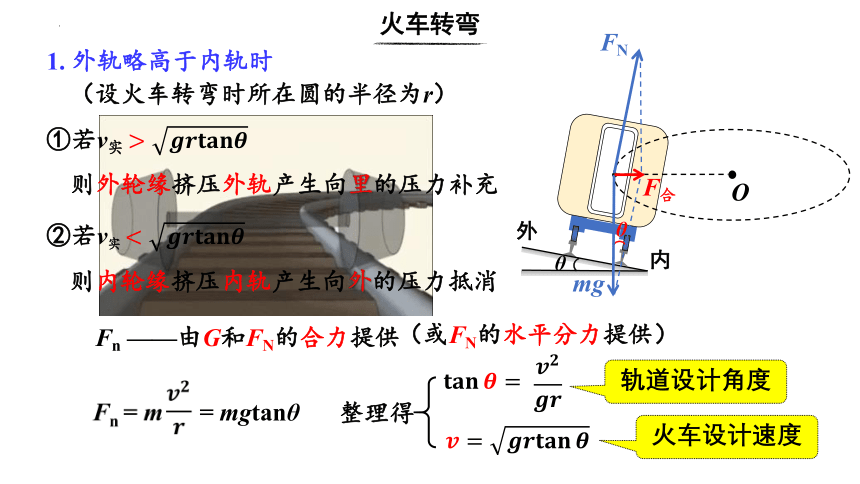
1. 外轨略高于内轨时
Fn ——由G和FN的合力提供
(或FN的水平分力提供)
(
θ
轨道设计角度
①若v实
则外轮缘挤压外轨产生向里的压力补充
②若v实
则内轮缘挤压内轨产生向外的压力抵消
火车转弯
整理得
火车设计速度
= mgtanθ
(设火车转弯时所在圆的半径为r)
O
FN
mg
F合
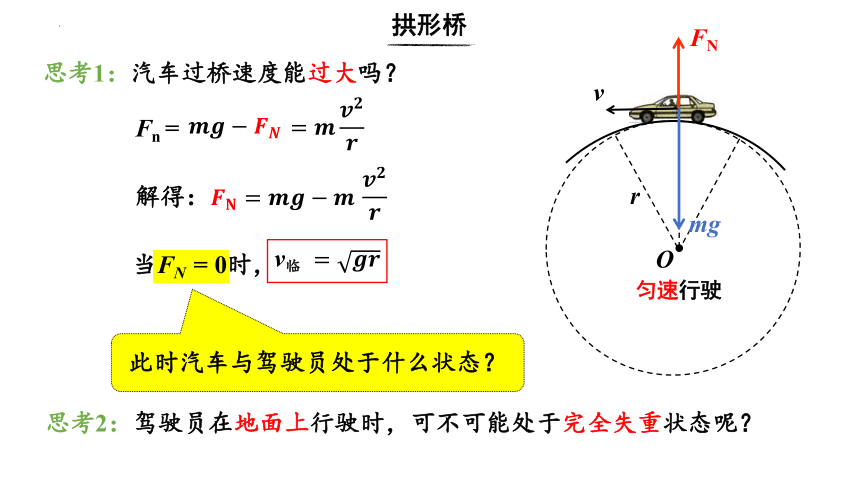
拱形桥
O
v
r
匀速行驶
mg
FN
Fn =
拱形桥
解得:
向心力表达式:
(设汽车驶过拱形桥顶点的速度为v,顶点所在圆的半径为r)
支持力小于重力
Fn =
思考1:汽车过桥速度能过大吗?
当FN = 0时,
v临
拱形桥
解得:
思考2:驾驶员在地面上行驶时,可不可能处于完全失重状态呢?
此时汽车与驾驶员处于什么状态?
O
v
r
匀速行驶
mg
FN
拓展:地球可否看成一个巨大的拱形桥?
当FN = 0时,
v临
mg
FN
会不会出现这种情况:速度大到一定程度时,地面对车的支持力为零?
m/s
此时:驾驶员处于什么状态?
——完全失重
拱形桥
Fn =
解得:
(地球半径约为6400km)
≈ 8000m/s
r
F引
思考:航天器中人的失重,是因为摆脱了地球的引力吗?
Fn =
FN = 0
当v
对航天员分析:
航天器中失重现象
解得:
故人处于完全失重状态
俯 视 图
FN
≈ mg
≈ 8000m/s时,
O
凹形桥
O
匀速行驶
v
r
mg
FN
Fn =
支持力大于重力
凹形桥
解得:
(设汽车驶过凹形桥最低点的速度为v,最低点所在圆的半径为r)
向心力表达式:
游戏挑战——用杯子把小钢球 “吸”起来
F需
F合 =
<
同学们,下课!
第六章 抛体运动
第4节 生活中的圆周运动(2)
h
(
θ
例1. 火车以半径R=900m转弯,火车质量为8×105kg,速度为30m/s,火车轨距l=1.4m,要使火车通过弯道时仅受重力与轨道的支持力,轨道应该垫起的高度h为多大?
FN
mg
F合
(
θ
解:
当θ较小时tanθ = sinθ
Fn = mgtanθ
∴h = 0.14m
巩固与练习
Fn = m
例2. 火车转弯可近似看成是做匀速圆周运动,当火车速度提高时会使轨道的外轨受损。为解决火车高速转弯时不使外轨受损这一难题,你认为以下措施可行的是( )
A.适当增高内轨
B.适当降低外轨
C.减小弯道半径
D.增大弯道半径
D
巩固与练习
T
G
G1
G2
竖直平面内的圆周运动
ω
匀速圆周运动:
非匀速圆周运动
F切 = ma切
F合=
高考只要求最高点和最低点
竖直平面内的圆周运动
管子
轻杆
细绳
圆环
杆模型
绳模型
(双向约束)
(单向约束)
过最低点
过最高点
v临时,
FN = 0,
此时,
FN为支持力
FN为拉力
最高点速度
(超重)
(产生指向圆心的拉力或支持力)
(完全失重)
时,
时,
例1. 如图所示,质量m=0.1kg的小桶固定于90cm长的轻绳的一端,使它在竖直面内绕绳的另一端做圆周运动。(g取10m/s2)
(1)若木桶通过最高点时的速度大小为3m/s,则此时绳受到木桶的作用力的大小和方向如何?
(2)若木桶通过最高点时的速度大小为2m/s,此时情况如何?
(3)若木桶内盛有M=0.4kg的水,则当木桶以4m/s的速度通过最高点时,轻绳和水对桶的作用力各为多大?
G
T
G水
FN
巩固与练习
例2. 如图所示,质量m=0.1kg的小桶固定于90cm长的轻杆的一端,使它在竖直面内绕杆的另一端做圆周运动。(g取10m/s2)
(1)若木桶通过最高点时的速度大小为3m/s,则此时杆受到木桶的作用力的大小和方向如何?
(2)若木桶通过最高点时的速度大小为2m/s,此时情况如何?
(3)若木桶内盛有M=0.4kg的水,则当木桶以4m/s的速度通过最高点时,轻杆和水对桶的作用力各为多大?
巩固与练习
FT=0
FTv
光滑水平面上运动
FT
离心运动:
当合外力突然消失或不足以提供所需向心力时,物体逐渐远离圆心的运动。
(a=0)
(a≠0)
离心运动时,速度变化情况可能如何?
离心运动时,是因为受到离心力吗?
FT
v
FT=0
FTFT>Fn
v
光滑水平面上运动
FT
离心运动:
当合外力突然消失或不足以提供所需向心力时,物体逐渐远离圆心的运动。
向心运动:
当合外力大于所需向心力时,物体逐渐靠近圆心的运动。
(a=0)
(a≠0)
FT
v
同学们,下课!
例1.如图所示,质量为m的滑块从半径为R的光滑固定圆形轨道的A点滑下。若它在下滑时经过B点的速度为v,则滑块下滑过程中:
(1)线速度如何变化?为什么?
(2)角速度如何变化?经过B点时角速度多大?
(3)向心加速度如何变化?切向加速度又如何?
(4)经过B点时所受的合力是否等于mv2/R?
非匀速圆周运动
B
A
圆周运动动力学问题
P30-4. 如图所示,金属环M、N用不可伸长的细线连接,分别套在水平粗糙细杆和竖直光滑细杆上,当整个装置以竖直杆为轴、以不同大小的角速度匀速转动时,两金属环一直相对杆不动,下列判断正确的是( )
A. 转动的角速度越大,细线中的拉力越大
B. 转动的角速度越大,环M与水平杆之间的弹力越大
C. 转动的角速度越大,环N与竖直杆之间的弹力越大
D. 转动的角速度不同,环M与水平杆之间的摩擦力大小可能相等
第六章 圆周运动
第4节 生活中的圆周运动(1)
思考1:汽车转弯时可看成圆周运动,是什么力使它产生向心力呢?
O
思考2:如果汽车速度过快会发生什么呢?
Ff
Fn =
思考3:如何能减少这种情况的发生?
思考:高速公路转弯处和赛道转弯处,路面往往有一定的倾斜度,你们知道
这样设计的原因是什么吗?
赛道转弯处
高速公路转弯处
F合
当车速很快时转弯,容易发生侧滑或翻车,那是因为车的合力不足以提供转弯时的向心力,当路面有一定的倾斜度时,就可以用车受到的重力与支持力的合力充当一部分向心力,可减少侧滑或翻车的情况。
O
= Fn
FN
G
1. 内外轨道一样高时
F
火车转弯
思考:火车转弯时也可看成做圆周运动,是什么力使它产生向心力呢?
我是铁路设计师
(
θ
外
内
1. 外轨略高于内轨时
Fn ——由G和FN的合力提供
(或FN的水平分力提供)
(
θ
轨道设计角度
①若v实
则外轮缘挤压外轨产生向里的压力补充
②若v实
则内轮缘挤压内轨产生向外的压力抵消
火车转弯
整理得
火车设计速度
= mgtanθ
(设火车转弯时所在圆的半径为r)
O
FN
mg
F合
拱形桥
O
v
r
匀速行驶
mg
FN
Fn =
拱形桥
解得:
向心力表达式:
(设汽车驶过拱形桥顶点的速度为v,顶点所在圆的半径为r)
支持力小于重力
Fn =
思考1:汽车过桥速度能过大吗?
当FN = 0时,
v临
拱形桥
解得:
思考2:驾驶员在地面上行驶时,可不可能处于完全失重状态呢?
此时汽车与驾驶员处于什么状态?
O
v
r
匀速行驶
mg
FN
拓展:地球可否看成一个巨大的拱形桥?
当FN = 0时,
v临
mg
FN
会不会出现这种情况:速度大到一定程度时,地面对车的支持力为零?
m/s
此时:驾驶员处于什么状态?
——完全失重
拱形桥
Fn =
解得:
(地球半径约为6400km)
≈ 8000m/s
r
F引
思考:航天器中人的失重,是因为摆脱了地球的引力吗?
Fn =
FN = 0
当v
对航天员分析:
航天器中失重现象
解得:
故人处于完全失重状态
俯 视 图
FN
≈ mg
≈ 8000m/s时,
O
凹形桥
O
匀速行驶
v
r
mg
FN
Fn =
支持力大于重力
凹形桥
解得:
(设汽车驶过凹形桥最低点的速度为v,最低点所在圆的半径为r)
向心力表达式:
游戏挑战——用杯子把小钢球 “吸”起来
F需
F合 =
<
同学们,下课!
第六章 抛体运动
第4节 生活中的圆周运动(2)
h
(
θ
例1. 火车以半径R=900m转弯,火车质量为8×105kg,速度为30m/s,火车轨距l=1.4m,要使火车通过弯道时仅受重力与轨道的支持力,轨道应该垫起的高度h为多大?
FN
mg
F合
(
θ
解:
当θ较小时tanθ = sinθ
Fn = mgtanθ
∴h = 0.14m
巩固与练习
Fn = m
例2. 火车转弯可近似看成是做匀速圆周运动,当火车速度提高时会使轨道的外轨受损。为解决火车高速转弯时不使外轨受损这一难题,你认为以下措施可行的是( )
A.适当增高内轨
B.适当降低外轨
C.减小弯道半径
D.增大弯道半径
D
巩固与练习
T
G
G1
G2
竖直平面内的圆周运动
ω
匀速圆周运动:
非匀速圆周运动
F切 = ma切
F合=
高考只要求最高点和最低点
竖直平面内的圆周运动
管子
轻杆
细绳
圆环
杆模型
绳模型
(双向约束)
(单向约束)
过最低点
过最高点
v临时,
FN = 0,
此时,
FN为支持力
FN为拉力
最高点速度
(超重)
(产生指向圆心的拉力或支持力)
(完全失重)
时,
时,
例1. 如图所示,质量m=0.1kg的小桶固定于90cm长的轻绳的一端,使它在竖直面内绕绳的另一端做圆周运动。(g取10m/s2)
(1)若木桶通过最高点时的速度大小为3m/s,则此时绳受到木桶的作用力的大小和方向如何?
(2)若木桶通过最高点时的速度大小为2m/s,此时情况如何?
(3)若木桶内盛有M=0.4kg的水,则当木桶以4m/s的速度通过最高点时,轻绳和水对桶的作用力各为多大?
G
T
G水
FN
巩固与练习
例2. 如图所示,质量m=0.1kg的小桶固定于90cm长的轻杆的一端,使它在竖直面内绕杆的另一端做圆周运动。(g取10m/s2)
(1)若木桶通过最高点时的速度大小为3m/s,则此时杆受到木桶的作用力的大小和方向如何?
(2)若木桶通过最高点时的速度大小为2m/s,此时情况如何?
(3)若木桶内盛有M=0.4kg的水,则当木桶以4m/s的速度通过最高点时,轻杆和水对桶的作用力各为多大?
巩固与练习
FT=0
FT
光滑水平面上运动
FT
离心运动:
当合外力突然消失或不足以提供所需向心力时,物体逐渐远离圆心的运动。
(a=0)
(a≠0)
离心运动时,速度变化情况可能如何?
离心运动时,是因为受到离心力吗?
FT
v
FT=0
FT
v
光滑水平面上运动
FT
离心运动:
当合外力突然消失或不足以提供所需向心力时,物体逐渐远离圆心的运动。
向心运动:
当合外力大于所需向心力时,物体逐渐靠近圆心的运动。
(a=0)
(a≠0)
FT
v
同学们,下课!
例1.如图所示,质量为m的滑块从半径为R的光滑固定圆形轨道的A点滑下。若它在下滑时经过B点的速度为v,则滑块下滑过程中:
(1)线速度如何变化?为什么?
(2)角速度如何变化?经过B点时角速度多大?
(3)向心加速度如何变化?切向加速度又如何?
(4)经过B点时所受的合力是否等于mv2/R?
非匀速圆周运动
B
A
圆周运动动力学问题
P30-4. 如图所示,金属环M、N用不可伸长的细线连接,分别套在水平粗糙细杆和竖直光滑细杆上,当整个装置以竖直杆为轴、以不同大小的角速度匀速转动时,两金属环一直相对杆不动,下列判断正确的是( )
A. 转动的角速度越大,细线中的拉力越大
B. 转动的角速度越大,环M与水平杆之间的弹力越大
C. 转动的角速度越大,环N与竖直杆之间的弹力越大
D. 转动的角速度不同,环M与水平杆之间的摩擦力大小可能相等
