八年级数学北师大版上册 第七章 平行线的证明复习 课件(共28张PPT)
文档属性
| 名称 | 八年级数学北师大版上册 第七章 平行线的证明复习 课件(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 273.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-18 11:32:00 | ||
图片预览








文档简介
(共28张PPT)
平行线的证明
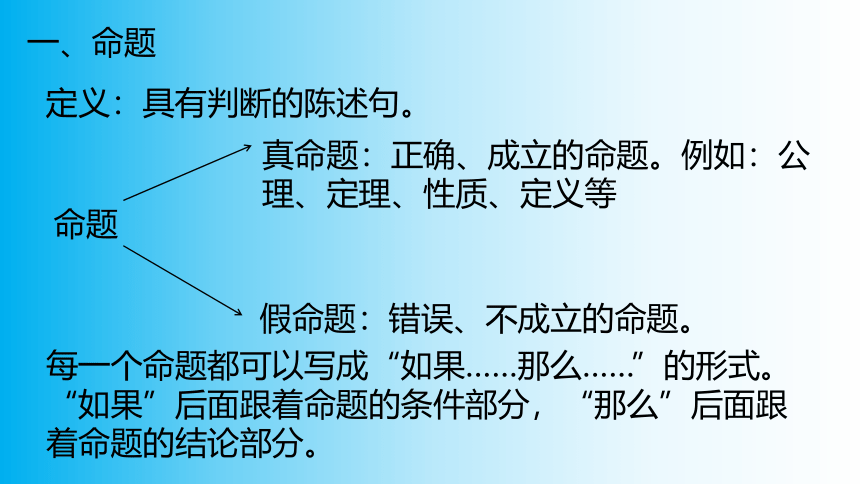
一、命题
定义:具有判断的陈述句。
命题
真命题:正确、成立的命题。例如:公理、定理、性质、定义等
假命题:错误、不成立的命题。
每一个命题都可以写成“如果……那么……”的形式。
“如果”后面跟着命题的条件部分,“那么”后面跟着命题的结论部分。
例1.下列句子中不是命题的是( )
A.两直线平行,同位角相等
B.直线AB垂直于CD吗
C.若|a|=|b|,则=
D.同角的补角相等
B
例2.把下列命题改写成“如果……那么……”的形式.
(1)绝对值相等的两个数一定相等;
(2)在同一平面内,垂直于同一条直线的两条直线平行.
解:
(1)如果两个数的绝对值相等,那么这两个数一定相等.
(2)在同一平面内,如果两条直线垂直于同一条直线,那么这两条直线平行.
例3.下列命题是真命题的是( )
A.若=,则a=b
B.若x=y,则2-3x>2-3y
C.若=2,则x=±
D.若=8,则x=±2
C
二、平行线的判定和性质
1.平行线的判定
①在同一平面中,垂直于同一直线的两直线平行。
②同位角相等,两直线平行。
③内错角相等,两直线平行。
④同旁内角互补,两直线平行。
例4、如图,直线AB,CD被直线EF所截,∠1=∠2,AB∥CD吗?为什么?
解:AB∥CD,理由如下:
∵∠1=∠3,∠1=∠2,
∴∠2=∠3,∴AB∥CD.
例5、如图,已知∠AED=60°,∠2=30°,EF平分∠AED,可以判断EF∥BD吗?为什么?
解:EF∥BD,理由如下:
∵∠AED=60°,EF平分∠AED,∴∠FED=30°.
又∵∠2=30°,∴∠FED=∠2,
∴EF∥BD.
例6、如图,∠1=70°,∠2=110°,AB与ED平行吗?为什么?
解:AB与ED平行,理由如下:
∵∠1=70°,∴∠AOD=70°.
∵∠2=110°,∴∠AOD+∠2=180°,
∴AB∥ED.
2.平行线的性质
①平行线的传递性:平行于同一直线的两直线平行。
②两直线平行,同位角相等。
③两直线平行,内错角相等。
④两直线平行,同旁内角互补。
例7、如图,已知AB∥CD,∠1=150°,则∠2= .
30°
例8、如图,在△ABC中,DE∥BC,∠EDC=40°,∠ECD=45°,则∠ACB= .
85°
三、三角形内角和定理
定理:三角形的内角和为180 。
推论1:三角形的一个外角等于与它不相邻的两个内角之和。
推论2:三角形的一个外角大于与它不相邻的任意一个内角。
例9、证明三角形的内角和定理.
如图,已知△ABC,求证:∠A+∠B+∠C=180°.
证明:过点A作EF∥BC,
∵EF∥BC,
∴∠EAB=∠B,∠FAC=∠C.
∵∠EAB+∠FAC+∠BAC=180°,
∴∠BAC+∠B+∠C=180°.
即三角形内角和等于180°.
例10、如图,在△ABC中,∠A=70°,∠B=60°,点D在BC的延长线上,则∠ACD等于( )
C
A.100° B.120°
C.130° D.150°
B
D
C
B
100°
60°
113°
两直线平行,内错角相等
等量代换
DF
同位角相等,两直线平行
两直线平行,同旁内角互补
BE
谢 谢
平行线的证明
一、命题
定义:具有判断的陈述句。
命题
真命题:正确、成立的命题。例如:公理、定理、性质、定义等
假命题:错误、不成立的命题。
每一个命题都可以写成“如果……那么……”的形式。
“如果”后面跟着命题的条件部分,“那么”后面跟着命题的结论部分。
例1.下列句子中不是命题的是( )
A.两直线平行,同位角相等
B.直线AB垂直于CD吗
C.若|a|=|b|,则=
D.同角的补角相等
B
例2.把下列命题改写成“如果……那么……”的形式.
(1)绝对值相等的两个数一定相等;
(2)在同一平面内,垂直于同一条直线的两条直线平行.
解:
(1)如果两个数的绝对值相等,那么这两个数一定相等.
(2)在同一平面内,如果两条直线垂直于同一条直线,那么这两条直线平行.
例3.下列命题是真命题的是( )
A.若=,则a=b
B.若x=y,则2-3x>2-3y
C.若=2,则x=±
D.若=8,则x=±2
C
二、平行线的判定和性质
1.平行线的判定
①在同一平面中,垂直于同一直线的两直线平行。
②同位角相等,两直线平行。
③内错角相等,两直线平行。
④同旁内角互补,两直线平行。
例4、如图,直线AB,CD被直线EF所截,∠1=∠2,AB∥CD吗?为什么?
解:AB∥CD,理由如下:
∵∠1=∠3,∠1=∠2,
∴∠2=∠3,∴AB∥CD.
例5、如图,已知∠AED=60°,∠2=30°,EF平分∠AED,可以判断EF∥BD吗?为什么?
解:EF∥BD,理由如下:
∵∠AED=60°,EF平分∠AED,∴∠FED=30°.
又∵∠2=30°,∴∠FED=∠2,
∴EF∥BD.
例6、如图,∠1=70°,∠2=110°,AB与ED平行吗?为什么?
解:AB与ED平行,理由如下:
∵∠1=70°,∴∠AOD=70°.
∵∠2=110°,∴∠AOD+∠2=180°,
∴AB∥ED.
2.平行线的性质
①平行线的传递性:平行于同一直线的两直线平行。
②两直线平行,同位角相等。
③两直线平行,内错角相等。
④两直线平行,同旁内角互补。
例7、如图,已知AB∥CD,∠1=150°,则∠2= .
30°
例8、如图,在△ABC中,DE∥BC,∠EDC=40°,∠ECD=45°,则∠ACB= .
85°
三、三角形内角和定理
定理:三角形的内角和为180 。
推论1:三角形的一个外角等于与它不相邻的两个内角之和。
推论2:三角形的一个外角大于与它不相邻的任意一个内角。
例9、证明三角形的内角和定理.
如图,已知△ABC,求证:∠A+∠B+∠C=180°.
证明:过点A作EF∥BC,
∵EF∥BC,
∴∠EAB=∠B,∠FAC=∠C.
∵∠EAB+∠FAC+∠BAC=180°,
∴∠BAC+∠B+∠C=180°.
即三角形内角和等于180°.
例10、如图,在△ABC中,∠A=70°,∠B=60°,点D在BC的延长线上,则∠ACD等于( )
C
A.100° B.120°
C.130° D.150°
B
D
C
B
100°
60°
113°
两直线平行,内错角相等
等量代换
DF
同位角相等,两直线平行
两直线平行,同旁内角互补
BE
谢 谢
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
