初中数学总复习--三角形及全等三角形复习[下学期]
文档属性
| 名称 | 初中数学总复习--三角形及全等三角形复习[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 284.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-11 15:31:00 | ||
图片预览


文档简介
(共17张PPT)
三角形及全等三角形复习
(1)了解三角形有关概念(内角、外角、中线、高、角平 分线),会画出任意三角形的角平分线、中线和高。
(2)掌握三角形中位线定理。
(3)了解全等三角形的概念,掌握两个三角形全等的判定定理。
考试内容:
三角形,三角形的角平分线、中线和高,三角形中位线,全等三角形、全等三角形的判定.
考试要求:
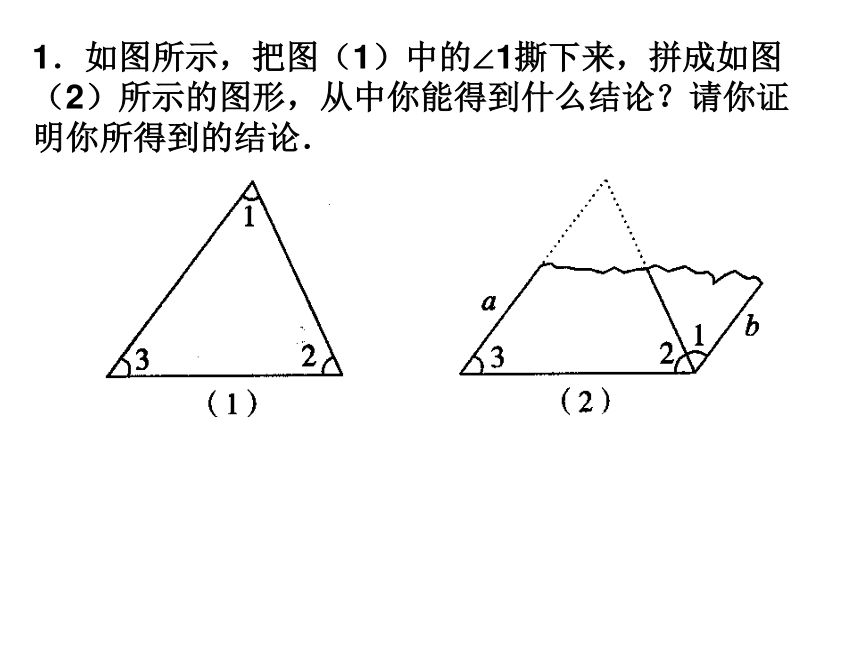
1.如图所示,把图(1)中的∠1撕下来,拼成如图(2)所示的图形,从中你能得到什么结论?请你证明你所得到的结论.
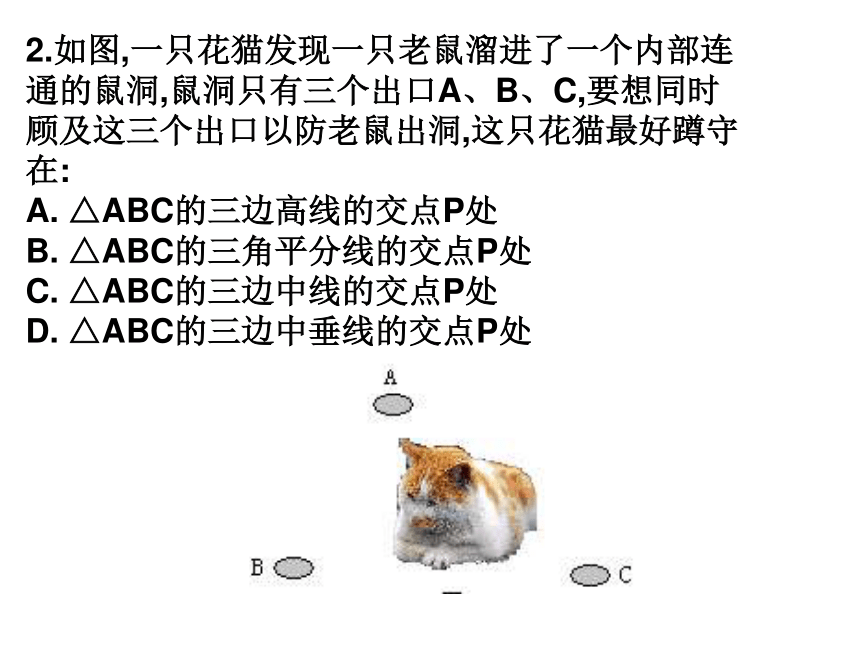
2.如图,一只花猫发现一只老鼠溜进了一个内部连通的鼠洞,鼠洞只有三个出口A、B、C,要想同时顾及这三个出口以防老鼠出洞,这只花猫最好蹲守在:
A. △ABC的三边高线的交点P处
B. △ABC的三角平分线的交点P处
C. △ABC的三边中线的交点P处
D. △ABC的三边中垂线的交点P处
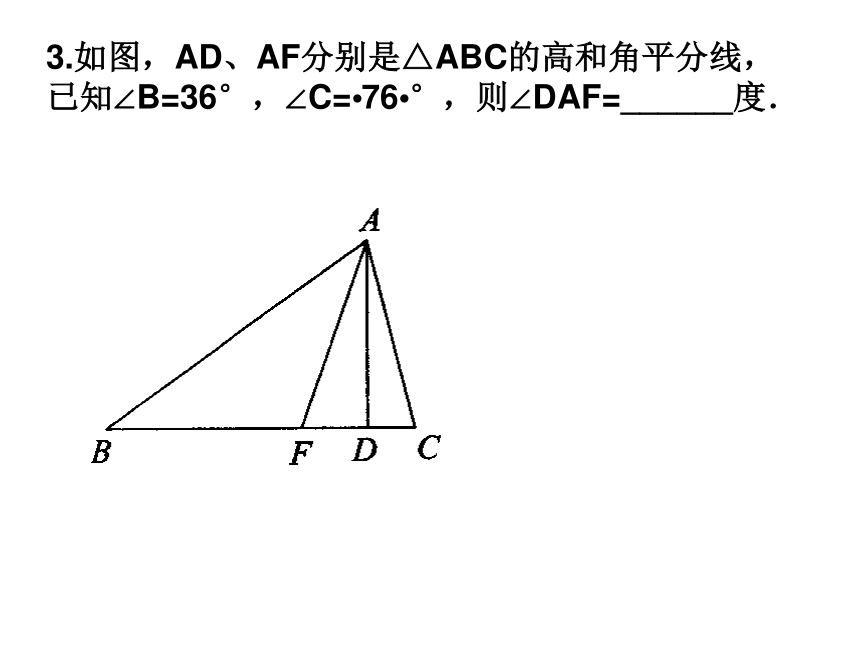
3.如图,AD、AF分别是△ABC的高和角平分线,已知∠B=36°,∠C=76°,则∠DAF=______度.
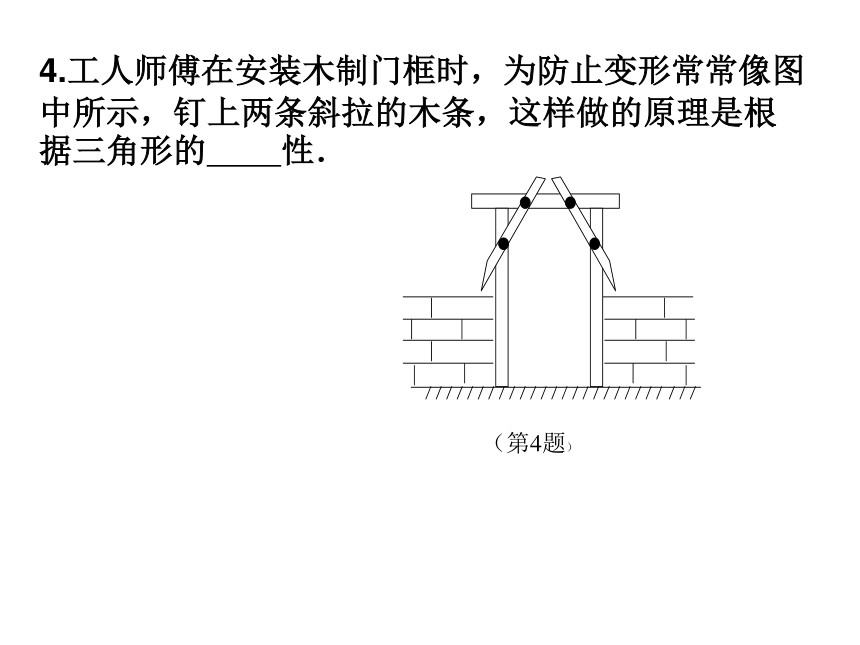
4.工人师傅在安装木制门框时,为防止变形常常像图中所示,钉上两条斜拉的木条,这样做的原理是根据三角形的 性.
(第4题)
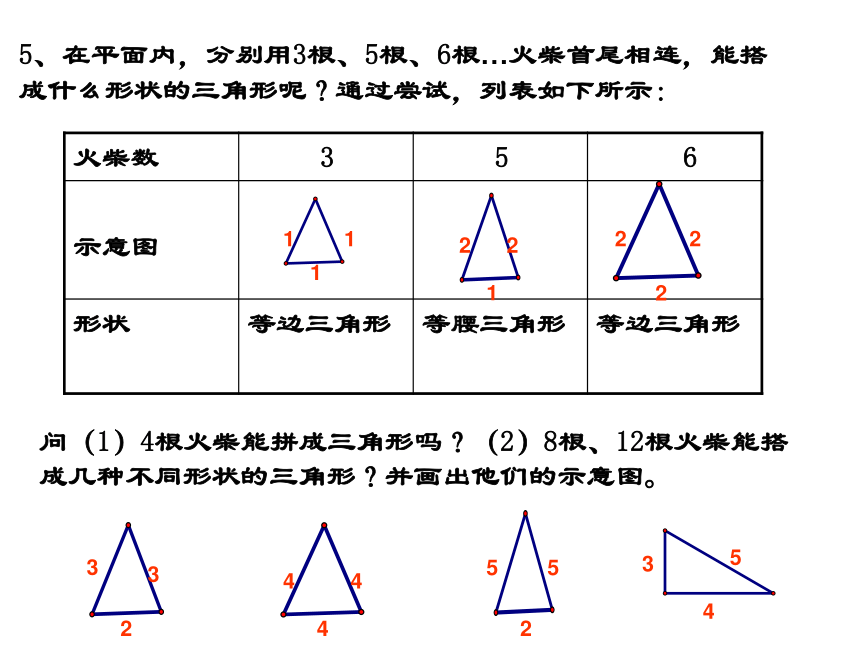
5、在平面内,分别用3根、5根、6根…火柴首尾相连,能搭成什么形状的三角形呢?通过尝试,列表如下所示:
火柴数 3 5 6
示意图
形状 等边三角形 等腰三角形 等边三角形
1
1
1
1
2
2
2
2
2
问(1)4根火柴能拼成三角形吗?(2)8根、12根火柴能搭成几种不同形状的三角形?并画出他们的示意图。
3
3
2
4
4
4
5
5
2
3
4
5
6.如图,△ABC是不等边三角形DE=BC,以D、E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形可以画出 ( )
A.2个 B.4个 C.6个 D.8个
7.如图,△ABC与△ABD中, AD与BC相交于O点,∠1=∠2,请你添加一个条件(不再添加其它线段,不再标注或使用其他字母),使AC=BD,并给出证明.
你添加的条件是: .
全等三角形的定义:
能够完全重合的两个三角形叫做全等三角形。
全等三角形的性质:
知识点
全等三角形的对应边、对应角相等;
全等三角形的对应角平分线、对应中线、对应高线相等;
全等三角形的面积周长也对应相等。
8.如图,D是△ABC的边AB上的一点,DF交AC于点E,给出3个论断:①DE=EF;②AD=CF;③FC∥AB,以其中一个论断为结论,其余两个论断为条件,可作出3个命题,请你写出所有真命题,并挑选其中的一个说明理由。
A
B
C
D
E
F
9.将边长为2的正△ABD沿BD所在直线翻折到右边,得△CBD,E、F分别
是AD上(异于点A、D)、CD上(异于点C、D)的两个动点,且满足AE+CF=2。
(1) 求证:△BED与△BFC全等;
(2) 探究:点E、F移动过程中,∠BEF的大小是否变化?若不变,则∠BEF = _________;若变化,请说明理由;
(3) 求△BEF周长的取值范围。
10.如图,小明想用皮尺测最池塘A、B间的距离,但现有皮尺无法直接测量,学习数学有关知识后,他想出了一个主意:先在地上取一个可以直接到达A、B两点的点O,连接OA、OB,分别在OA、OB上取中点C、D,连接CD,并测得CD = a,由此他即知道A、B距离是( )
A. 0.5a B.2a C.a D.3a
11.如图2,在△ABC中,∠C=90°,AD平分∠CAB,BC=8cm,BD=5cm,那么D点到直线AB的距离是_______cm.
12.已知等腰三角形的腰长是6cm,底边长是8cm,那么以各边中点为顶点的三角形的周长是 .
13.一个三角形的两边长分别为3和7,且第三边长为整数,这样的三角形的周长最小值是( )
14.如图,在Rt△ABC中,∠C = 90°,AC = 4,BC = 3。在Rt△ABC的外部拼接一个合适的直角三角形,使得拼成的图形是一个等腰三角形,如图所示.
15.如图12,在⊿ABC中,AB=AC,D是BC上任意一点,过D分别AB、AC向引垂线,垂足分别为E 、F,CG是边AB上的高.
A
G
E
B
D
F
图12
C
(1)DE,DF,CG的长之间存在着怎样的等量关系?并加以证明.
(2)若D在底边BC的延长线上,(1)中的结论还成立吗?若不成立,又存在怎样的关系?请说明理由.
三角形及全等三角形复习
(1)了解三角形有关概念(内角、外角、中线、高、角平 分线),会画出任意三角形的角平分线、中线和高。
(2)掌握三角形中位线定理。
(3)了解全等三角形的概念,掌握两个三角形全等的判定定理。
考试内容:
三角形,三角形的角平分线、中线和高,三角形中位线,全等三角形、全等三角形的判定.
考试要求:
1.如图所示,把图(1)中的∠1撕下来,拼成如图(2)所示的图形,从中你能得到什么结论?请你证明你所得到的结论.
2.如图,一只花猫发现一只老鼠溜进了一个内部连通的鼠洞,鼠洞只有三个出口A、B、C,要想同时顾及这三个出口以防老鼠出洞,这只花猫最好蹲守在:
A. △ABC的三边高线的交点P处
B. △ABC的三角平分线的交点P处
C. △ABC的三边中线的交点P处
D. △ABC的三边中垂线的交点P处
3.如图,AD、AF分别是△ABC的高和角平分线,已知∠B=36°,∠C=76°,则∠DAF=______度.
4.工人师傅在安装木制门框时,为防止变形常常像图中所示,钉上两条斜拉的木条,这样做的原理是根据三角形的 性.
(第4题)
5、在平面内,分别用3根、5根、6根…火柴首尾相连,能搭成什么形状的三角形呢?通过尝试,列表如下所示:
火柴数 3 5 6
示意图
形状 等边三角形 等腰三角形 等边三角形
1
1
1
1
2
2
2
2
2
问(1)4根火柴能拼成三角形吗?(2)8根、12根火柴能搭成几种不同形状的三角形?并画出他们的示意图。
3
3
2
4
4
4
5
5
2
3
4
5
6.如图,△ABC是不等边三角形DE=BC,以D、E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形可以画出 ( )
A.2个 B.4个 C.6个 D.8个
7.如图,△ABC与△ABD中, AD与BC相交于O点,∠1=∠2,请你添加一个条件(不再添加其它线段,不再标注或使用其他字母),使AC=BD,并给出证明.
你添加的条件是: .
全等三角形的定义:
能够完全重合的两个三角形叫做全等三角形。
全等三角形的性质:
知识点
全等三角形的对应边、对应角相等;
全等三角形的对应角平分线、对应中线、对应高线相等;
全等三角形的面积周长也对应相等。
8.如图,D是△ABC的边AB上的一点,DF交AC于点E,给出3个论断:①DE=EF;②AD=CF;③FC∥AB,以其中一个论断为结论,其余两个论断为条件,可作出3个命题,请你写出所有真命题,并挑选其中的一个说明理由。
A
B
C
D
E
F
9.将边长为2的正△ABD沿BD所在直线翻折到右边,得△CBD,E、F分别
是AD上(异于点A、D)、CD上(异于点C、D)的两个动点,且满足AE+CF=2。
(1) 求证:△BED与△BFC全等;
(2) 探究:点E、F移动过程中,∠BEF的大小是否变化?若不变,则∠BEF = _________;若变化,请说明理由;
(3) 求△BEF周长的取值范围。
10.如图,小明想用皮尺测最池塘A、B间的距离,但现有皮尺无法直接测量,学习数学有关知识后,他想出了一个主意:先在地上取一个可以直接到达A、B两点的点O,连接OA、OB,分别在OA、OB上取中点C、D,连接CD,并测得CD = a,由此他即知道A、B距离是( )
A. 0.5a B.2a C.a D.3a
11.如图2,在△ABC中,∠C=90°,AD平分∠CAB,BC=8cm,BD=5cm,那么D点到直线AB的距离是_______cm.
12.已知等腰三角形的腰长是6cm,底边长是8cm,那么以各边中点为顶点的三角形的周长是 .
13.一个三角形的两边长分别为3和7,且第三边长为整数,这样的三角形的周长最小值是( )
14.如图,在Rt△ABC中,∠C = 90°,AC = 4,BC = 3。在Rt△ABC的外部拼接一个合适的直角三角形,使得拼成的图形是一个等腰三角形,如图所示.
15.如图12,在⊿ABC中,AB=AC,D是BC上任意一点,过D分别AB、AC向引垂线,垂足分别为E 、F,CG是边AB上的高.
A
G
E
B
D
F
图12
C
(1)DE,DF,CG的长之间存在着怎样的等量关系?并加以证明.
(2)若D在底边BC的延长线上,(1)中的结论还成立吗?若不成立,又存在怎样的关系?请说明理由.
