苏科版七年级数学上册第6章平面图形的认识(一)单元测试卷(含答案)
文档属性
| 名称 | 苏科版七年级数学上册第6章平面图形的认识(一)单元测试卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-18 00:00:00 | ||
图片预览




文档简介
苏科版七年级数学上册单元测试卷
第6章平面图形的认识(一)
时间:120分 总分120分
一、选择题(每题3分,共24分)
1.手电简发射出来的光线,类似于几何中的 ( )
A.线段 B.射线 C.直线 D.折线
2.如图,则与的大小关系是 ( )
A. B. C. D.无法确定
3.如图,图中射线条数为 ( )
A.8 B.6 C.5 D.4
4.如图所示,的大小可由量角器测得,则图中的度数为( )
A. B. C. D.
5.某同学用剪刀沿直线将一片平整的银杏叶剪掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是
( )
A.两点确定一条直线 B.点动成线
C.直线是向两方无限延伸的 D.两点之间线段最短
6.角可以看成是由一条射线绕着它的端点旋转而成的,这体现了( )
A.点动成线 B.线动成面
C.面动成体 D.线线相交得点
7.已知点在线段上,则下列条件中,不能确定点是线段的中点的是 ( )
A. B. C. D.
8.已知,,则与的关系为 ( )
A.相等 B.互余 C.互补 D.以上都不对
二、填空题(每题3分,共24分)
9.若,则的补角等于______.
10.若平分,则__________.
11.如图,两块三角板的直角顶点重叠在一起,且,则的度数______.
12.时间为7点30分时,时针和分针形成的小于的角为___________°
13.如果∠A,∠B的两条边分别垂直,而其中∠A比∠B的4倍少30°,则∠B=_________.
14.如图,某海域有三个小岛A,B,O,在小岛O处观测到小岛A在它北偏东的方向上,观测到小岛B在它南偏东的方向上,则的度数大小是_____.
15.如果直线与直线交于点,且,,这两条直线的夹角是______度.
16.两根长度分别为6cm 和10cm 的直木条,将它们一端重合且放在同一条直线上,此时两根木条中点之间的距离为_________.
三、解答题(每题8分,共72分)
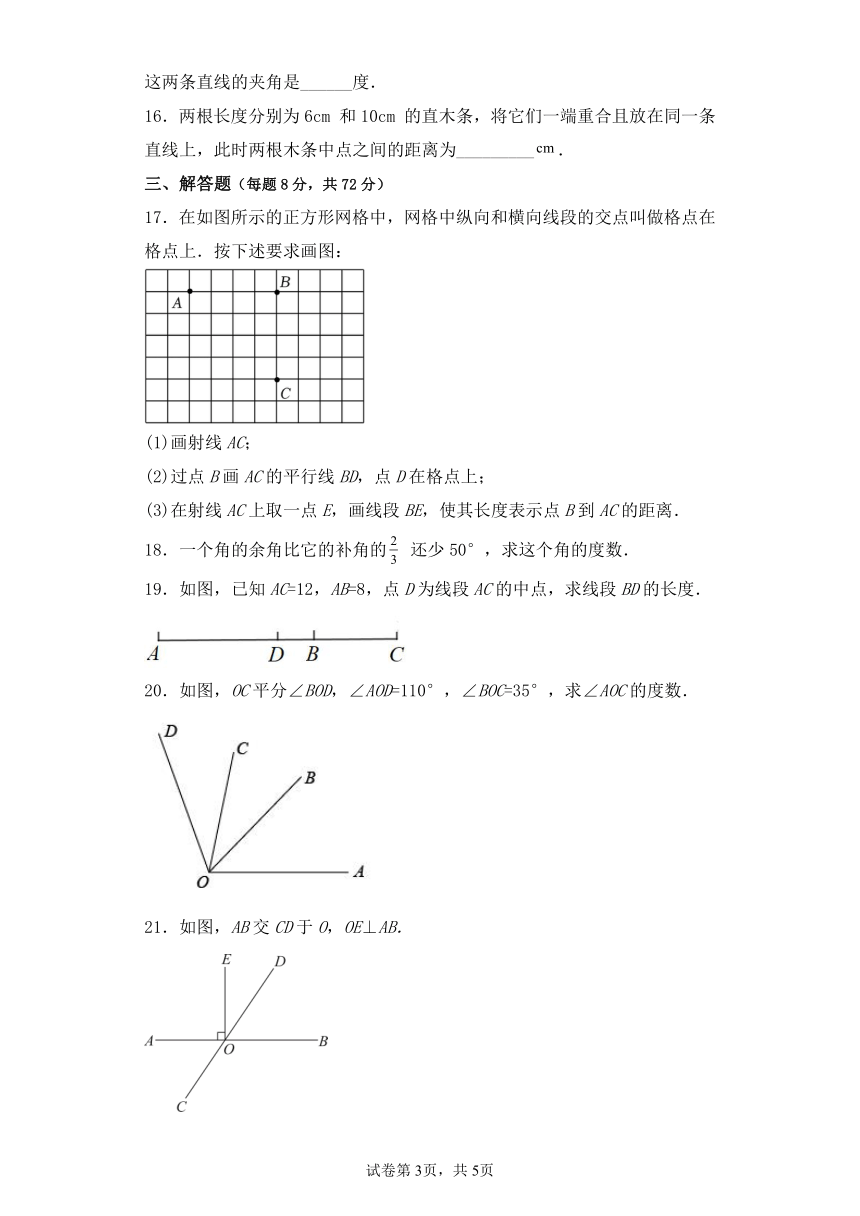
17.在如图所示的正方形网格中,网格中纵向和横向线段的交点叫做格点在格点上.按下述要求画图:
(1)画射线AC;
(2)过点B画AC的平行线BD,点D在格点上;
(3)在射线AC上取一点E,画线段BE,使其长度表示点B到AC的距离.
18.一个角的余角比它的补角的 还少50°,求这个角的度数.
19.如图,已知AC=12,AB=8,点D为线段AC的中点,求线段BD的长度.
20.如图,OC平分∠BOD,∠AOD=110°,∠BOC=35°,求∠AOC的度数.
21.如图,AB交CD于O,OE⊥AB.
(1)若∠EOD=30°,求∠AOC的度数;
(2)若∠EOD:∠EOC=1:3,求∠BOC的度数.
22.如图,已知线段上有两个定点B,C.
(1)图中共有____________条线段.
(2)若在线段上增加一点,则增加了_____________条线段.
(3)现有一列往返于A,B两地的火车,中途停靠五个站.问:①有____________种票价;②要准备____________种车票.
(4)已知A,B两地之间相距140km,在A,B所在的公路(看成直线)上有一处C,且B与C之间的距离为40km,M在A,C两地的正中间,求M与A地之间的距离.
23.如图,已知点O是直线上的一点,,射线是的角平分线,射线是的角平分线.
(1) = , = .
(2)求的度数;
(3)过点O作射线,若 求的度数.
24.如图,是内的一条射线,、分别平分、.
(1)若,,求的度数;
(2)若,,试猜想与、的数量关系并说明理由.
25.将一副直角三角板如图1摆放在直线上(直角三角板和直角三角板,,,,),保持三角板不动,将三角板绕点O以每秒的速度顺时针旋转(旋转过程中的大小保持不变)直至边第一次重合在直线上,整个过程时间记为t秒.
(1)从旋转开始至结束,整个过程共持续了______秒;
(2)如图2,旋转三角板,使得、在直线的异侧,请直接写出与数量关系;如图3,继续旋转三角板,使得、同时在直线的右侧,请问上面的数量关系是否仍然成立,并说明理由;
(3)若在三角板旋转的同时,另一个三角板也绕点O以每秒的速度顺时针旋转(旋转过程中的大小保持不变),当边第一次重合在直线上时两三角板同时停止.
①试用字母t分别表示与;
②在旋转的过程中,当t为何值时平分.
试卷第4页,共5页
试卷第12页,共9页
参考答案:
1.
解:手电简发射出来的光线,手电筒是射线的端点,光的传播方向是射线的方向,故手电简发射出来的光线,类似于几何中的是射线.
故选:B.
2.
解:∵,
∴,
∴,
故选:C.
3.
解:图中的射线有:射线,射线,射线,射线,射线,射线,射线,射线,
共8条,
故选:A.
4.
解:由题意,可得,
故选:C.
5.
解:根据两点之间,线段最短,可知剩下的银杏叶的周长比原银杏叶的周长要小,
故能正确解释这一现象的数学知识是两点之间,线段最短
故选D.
6.
解:角可以看成是由一条射线绕着它的端点旋转而成的,这体现了:线动成面,
故选:B.
7.
解:解:A、,则点P是线段中点;
B、,则点P是线段中点;
C、,则P可以是线段上任意一点;
D、,则点P是线段中点.
故选C.
8.
∵,
∴.
∴与互余.
故选:B.
9.
解:的补角,
故答案为:.
10.
解:如图,
∵平分,,
∴,
故答案为:
11.
解:,
∴,
∴,
故答案为:.
12.
解:分针速度:(度/分),时针速度:(度/分)
则7点30分时夹角为:.
故答案为:
13.
解:设∠B为x度,则∠A为(4x-30)度,
如图1,∵∠A+∠3=∠4+∠3=90°,
∴∠A=∠4,
∵∠4+∠5=180°,
∴∠A+∠5=180°,
即∠A+∠B=180°;
如图2,∵∠A+∠2=∠1+∠B=90°,∠1=∠2,
∴∠A=∠B.
综上所述,如果一个角的两边与另一个角的两边分别垂直,那么这两个角相等或互补.
∴4x-30=x 或4x-30+x=180,
解得:x=10或 x=42,
即∠B为10°或42°,
故答案为:10°或42°.
14.
解:根据题意,,
故答案为:.
15.
解:和是一对对顶角,
,
,
,
,
则,
,
故答案为:.
16.
解:如图,
设较长的木条为AB=10cm,较短的木条为BC=6cm,
∵M、N分别为AB、BC的中点,
∴BM=5cm,BN=3cm,
①如图1,BC不在AB上时,MN=BM+BN=5+3=8(cm),
②如图2,BC在AB上时,MN=BM-BN=5-3=2(cm),
综上所述,两根木条的中点间的距离是2cm 或8cm,
故答案为:2或8.
17.
解:(1)如图,射线AC即为所求;
(2)如图,直线BD即为所求;
(3)如图,线段BE即为所求.
18.
解:设这个角度数为x,它的余角为,补角为,根据题意得:
,
解得,
∴这个角度数为.
19.
解:因为AC=12,点D为线段AC的中点.
所以.
因为AB=8,
所以BD=AB-AD=8-6=2.
20.
解:∵OC平分∠BOD,∠BOC=35°,
∴∠BOD=2∠BOC=70°,
又∵∠AOD=110°,
∴∠AOB=∠AOD-∠BOD=40°,
∴∠AOC=∠AOB+∠BOC=40°+35°=75°.
21.
(1)
解:∵OE⊥AB,
∴∠AOE=90°,
∵∠AOC+∠AOE+∠DOE=180°,∠EOD=30°,
∴∠AOC=180°-∠AOE-∠DOE=180°-90°-30°=60°
(2)
设∠EOD=α,
∵∠EOD:∠EOC=1:3,
∴∠EOC=3α,
∵∠EOD+∠EOC=180°,
∴α+3α=180°,
∴∠EOD=α=45°,
∴∠AOD=∠AOE+∠DOE=135°
∵∠AOD与∠BOC为对顶角,
∴∠BOC=∠AOD=135°
22.
(1)解:图中有6条线段,线段.
故答案为:6;
(2)解:增加一个点后共有10条线段,
所以会增加4条线段.
故答案为:4;
(3)解:当直线m上有2个点时,线段的总条数为1,
直线m上有3个点时,线段的总条数为,
直线m上有4个点时,线段的总条数为,
…
由此得出当直线m上有n个点时,线段的总条数为,
①现有一列往返于A,B两地的火车,中途停靠五个站,
所以直线上共有7个点,共有线段(条),
所以共有21种票价;
②因车票需要考虑方向性,故需要准备车票的种类是票价的2倍,
所以(种),
所以共有42种票价.
故答案为:①21;②42;
(4)解:当点C在线段上时,如图:
∵,
∴,
∵M是的中点,
∴;
当点C在线段的延长线上时,如图:
∵,
∴,
∵M是的中点,
∴;
综上,或.
23.
(1)解:,,
,;
故答案为:,
(2)解:是的角平分线,射线是的角平分线,
,,
;
(3)解:;
当射线在内部时,如左图;
则;
当射线在内部时,如右图;
则;
综上,的度数为或.
24.
(1)解:,,
,
、分别平分、,,
,
,
;
(2),,
,
、分别平分、,
,
,
.
25.
(1)根据题意可知:(秒),
故答案为:9;
(2)∵,,,,
、在直线的异侧,如图2所示,
∵,,
∴,
∴即,
、在直线的右侧,仍成立.
理由如下:
如图3所示,∵,,
∴;
(3)当三角板旋转的同时,另一个三角板绕点O以每秒的速度顺时针旋转,
①当旋转t秒时,,,
∴.
②若平分,
则有,
根据①的结果列式:,
解得:.
答:在旋转的过程中,当t为秒时,平分.
第6章平面图形的认识(一)
时间:120分 总分120分
一、选择题(每题3分,共24分)
1.手电简发射出来的光线,类似于几何中的 ( )
A.线段 B.射线 C.直线 D.折线
2.如图,则与的大小关系是 ( )
A. B. C. D.无法确定
3.如图,图中射线条数为 ( )
A.8 B.6 C.5 D.4
4.如图所示,的大小可由量角器测得,则图中的度数为( )
A. B. C. D.
5.某同学用剪刀沿直线将一片平整的银杏叶剪掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是
( )
A.两点确定一条直线 B.点动成线
C.直线是向两方无限延伸的 D.两点之间线段最短
6.角可以看成是由一条射线绕着它的端点旋转而成的,这体现了( )
A.点动成线 B.线动成面
C.面动成体 D.线线相交得点
7.已知点在线段上,则下列条件中,不能确定点是线段的中点的是 ( )
A. B. C. D.
8.已知,,则与的关系为 ( )
A.相等 B.互余 C.互补 D.以上都不对
二、填空题(每题3分,共24分)
9.若,则的补角等于______.
10.若平分,则__________.
11.如图,两块三角板的直角顶点重叠在一起,且,则的度数______.
12.时间为7点30分时,时针和分针形成的小于的角为___________°
13.如果∠A,∠B的两条边分别垂直,而其中∠A比∠B的4倍少30°,则∠B=_________.
14.如图,某海域有三个小岛A,B,O,在小岛O处观测到小岛A在它北偏东的方向上,观测到小岛B在它南偏东的方向上,则的度数大小是_____.
15.如果直线与直线交于点,且,,这两条直线的夹角是______度.
16.两根长度分别为6cm 和10cm 的直木条,将它们一端重合且放在同一条直线上,此时两根木条中点之间的距离为_________.
三、解答题(每题8分,共72分)
17.在如图所示的正方形网格中,网格中纵向和横向线段的交点叫做格点在格点上.按下述要求画图:
(1)画射线AC;
(2)过点B画AC的平行线BD,点D在格点上;
(3)在射线AC上取一点E,画线段BE,使其长度表示点B到AC的距离.
18.一个角的余角比它的补角的 还少50°,求这个角的度数.
19.如图,已知AC=12,AB=8,点D为线段AC的中点,求线段BD的长度.
20.如图,OC平分∠BOD,∠AOD=110°,∠BOC=35°,求∠AOC的度数.
21.如图,AB交CD于O,OE⊥AB.
(1)若∠EOD=30°,求∠AOC的度数;
(2)若∠EOD:∠EOC=1:3,求∠BOC的度数.
22.如图,已知线段上有两个定点B,C.
(1)图中共有____________条线段.
(2)若在线段上增加一点,则增加了_____________条线段.
(3)现有一列往返于A,B两地的火车,中途停靠五个站.问:①有____________种票价;②要准备____________种车票.
(4)已知A,B两地之间相距140km,在A,B所在的公路(看成直线)上有一处C,且B与C之间的距离为40km,M在A,C两地的正中间,求M与A地之间的距离.
23.如图,已知点O是直线上的一点,,射线是的角平分线,射线是的角平分线.
(1) = , = .
(2)求的度数;
(3)过点O作射线,若 求的度数.
24.如图,是内的一条射线,、分别平分、.
(1)若,,求的度数;
(2)若,,试猜想与、的数量关系并说明理由.
25.将一副直角三角板如图1摆放在直线上(直角三角板和直角三角板,,,,),保持三角板不动,将三角板绕点O以每秒的速度顺时针旋转(旋转过程中的大小保持不变)直至边第一次重合在直线上,整个过程时间记为t秒.
(1)从旋转开始至结束,整个过程共持续了______秒;
(2)如图2,旋转三角板,使得、在直线的异侧,请直接写出与数量关系;如图3,继续旋转三角板,使得、同时在直线的右侧,请问上面的数量关系是否仍然成立,并说明理由;
(3)若在三角板旋转的同时,另一个三角板也绕点O以每秒的速度顺时针旋转(旋转过程中的大小保持不变),当边第一次重合在直线上时两三角板同时停止.
①试用字母t分别表示与;
②在旋转的过程中,当t为何值时平分.
试卷第4页,共5页
试卷第12页,共9页
参考答案:
1.
解:手电简发射出来的光线,手电筒是射线的端点,光的传播方向是射线的方向,故手电简发射出来的光线,类似于几何中的是射线.
故选:B.
2.
解:∵,
∴,
∴,
故选:C.
3.
解:图中的射线有:射线,射线,射线,射线,射线,射线,射线,射线,
共8条,
故选:A.
4.
解:由题意,可得,
故选:C.
5.
解:根据两点之间,线段最短,可知剩下的银杏叶的周长比原银杏叶的周长要小,
故能正确解释这一现象的数学知识是两点之间,线段最短
故选D.
6.
解:角可以看成是由一条射线绕着它的端点旋转而成的,这体现了:线动成面,
故选:B.
7.
解:解:A、,则点P是线段中点;
B、,则点P是线段中点;
C、,则P可以是线段上任意一点;
D、,则点P是线段中点.
故选C.
8.
∵,
∴.
∴与互余.
故选:B.
9.
解:的补角,
故答案为:.
10.
解:如图,
∵平分,,
∴,
故答案为:
11.
解:,
∴,
∴,
故答案为:.
12.
解:分针速度:(度/分),时针速度:(度/分)
则7点30分时夹角为:.
故答案为:
13.
解:设∠B为x度,则∠A为(4x-30)度,
如图1,∵∠A+∠3=∠4+∠3=90°,
∴∠A=∠4,
∵∠4+∠5=180°,
∴∠A+∠5=180°,
即∠A+∠B=180°;
如图2,∵∠A+∠2=∠1+∠B=90°,∠1=∠2,
∴∠A=∠B.
综上所述,如果一个角的两边与另一个角的两边分别垂直,那么这两个角相等或互补.
∴4x-30=x 或4x-30+x=180,
解得:x=10或 x=42,
即∠B为10°或42°,
故答案为:10°或42°.
14.
解:根据题意,,
故答案为:.
15.
解:和是一对对顶角,
,
,
,
,
则,
,
故答案为:.
16.
解:如图,
设较长的木条为AB=10cm,较短的木条为BC=6cm,
∵M、N分别为AB、BC的中点,
∴BM=5cm,BN=3cm,
①如图1,BC不在AB上时,MN=BM+BN=5+3=8(cm),
②如图2,BC在AB上时,MN=BM-BN=5-3=2(cm),
综上所述,两根木条的中点间的距离是2cm 或8cm,
故答案为:2或8.
17.
解:(1)如图,射线AC即为所求;
(2)如图,直线BD即为所求;
(3)如图,线段BE即为所求.
18.
解:设这个角度数为x,它的余角为,补角为,根据题意得:
,
解得,
∴这个角度数为.
19.
解:因为AC=12,点D为线段AC的中点.
所以.
因为AB=8,
所以BD=AB-AD=8-6=2.
20.
解:∵OC平分∠BOD,∠BOC=35°,
∴∠BOD=2∠BOC=70°,
又∵∠AOD=110°,
∴∠AOB=∠AOD-∠BOD=40°,
∴∠AOC=∠AOB+∠BOC=40°+35°=75°.
21.
(1)
解:∵OE⊥AB,
∴∠AOE=90°,
∵∠AOC+∠AOE+∠DOE=180°,∠EOD=30°,
∴∠AOC=180°-∠AOE-∠DOE=180°-90°-30°=60°
(2)
设∠EOD=α,
∵∠EOD:∠EOC=1:3,
∴∠EOC=3α,
∵∠EOD+∠EOC=180°,
∴α+3α=180°,
∴∠EOD=α=45°,
∴∠AOD=∠AOE+∠DOE=135°
∵∠AOD与∠BOC为对顶角,
∴∠BOC=∠AOD=135°
22.
(1)解:图中有6条线段,线段.
故答案为:6;
(2)解:增加一个点后共有10条线段,
所以会增加4条线段.
故答案为:4;
(3)解:当直线m上有2个点时,线段的总条数为1,
直线m上有3个点时,线段的总条数为,
直线m上有4个点时,线段的总条数为,
…
由此得出当直线m上有n个点时,线段的总条数为,
①现有一列往返于A,B两地的火车,中途停靠五个站,
所以直线上共有7个点,共有线段(条),
所以共有21种票价;
②因车票需要考虑方向性,故需要准备车票的种类是票价的2倍,
所以(种),
所以共有42种票价.
故答案为:①21;②42;
(4)解:当点C在线段上时,如图:
∵,
∴,
∵M是的中点,
∴;
当点C在线段的延长线上时,如图:
∵,
∴,
∵M是的中点,
∴;
综上,或.
23.
(1)解:,,
,;
故答案为:,
(2)解:是的角平分线,射线是的角平分线,
,,
;
(3)解:;
当射线在内部时,如左图;
则;
当射线在内部时,如右图;
则;
综上,的度数为或.
24.
(1)解:,,
,
、分别平分、,,
,
,
;
(2),,
,
、分别平分、,
,
,
.
25.
(1)根据题意可知:(秒),
故答案为:9;
(2)∵,,,,
、在直线的异侧,如图2所示,
∵,,
∴,
∴即,
、在直线的右侧,仍成立.
理由如下:
如图3所示,∵,,
∴;
(3)当三角板旋转的同时,另一个三角板绕点O以每秒的速度顺时针旋转,
①当旋转t秒时,,,
∴.
②若平分,
则有,
根据①的结果列式:,
解得:.
答:在旋转的过程中,当t为秒时,平分.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
