孝感市 等腰三角形复习[下学期]
文档属性
| 名称 | 孝感市 等腰三角形复习[下学期] | 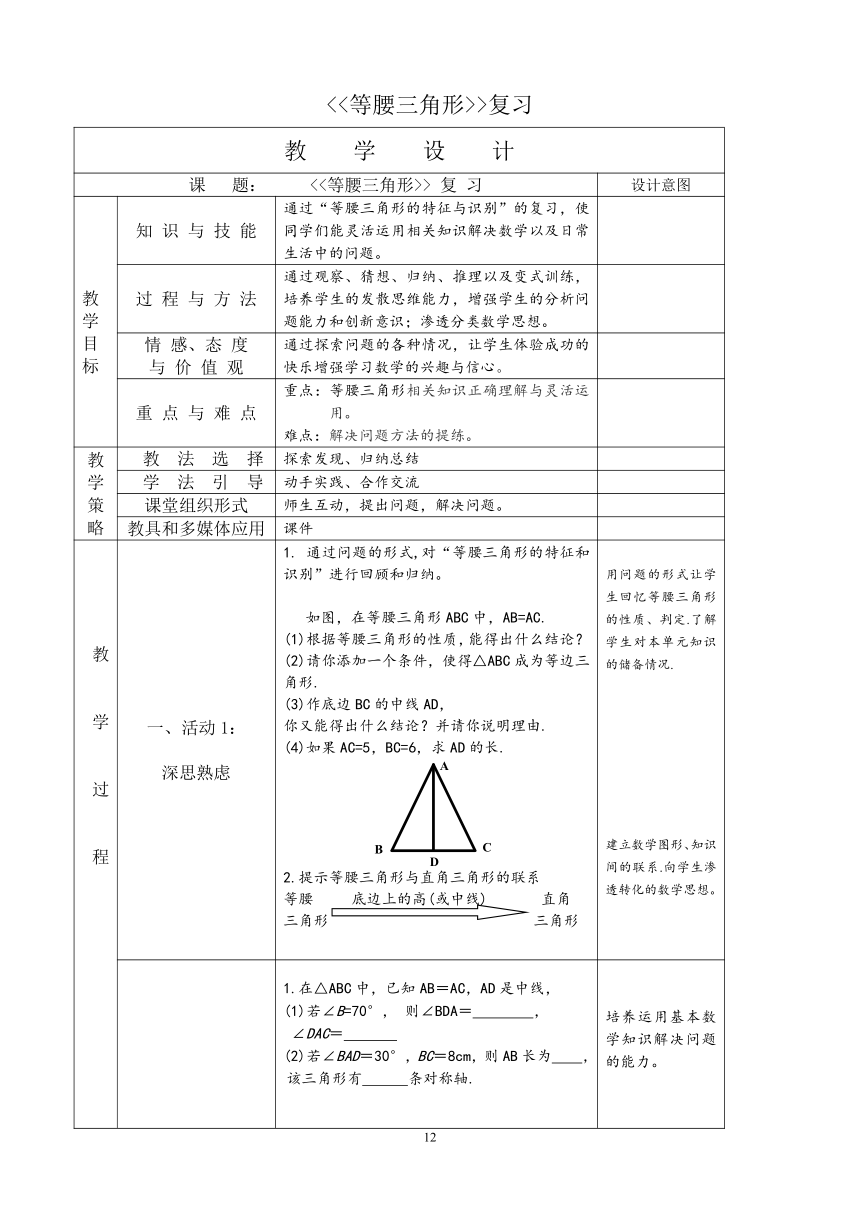 | |
| 格式 | rar | ||
| 文件大小 | 32.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-21 21:20:00 | ||
图片预览


文档简介
<<等腰三角形>>复习
教 学 设 计
课 题: <<等腰三角形>> 复 习 设计意图
教学目标 知 识 与 技 能 通过“等腰三角形的特征与识别”的复习,使同学们能灵活运用相关知识解决数学以及日常生活中的问题。
过 程 与 方 法 通过观察、猜想、归纳、推理以及变式训练,培养学生的发散思维能力,增强学生的分析问题能力和创新意识;渗透分类数学思想。
情 感、态 度与 价 值 观 通过探索问题的各种情况,让学生体验成功的快乐增强学习数学的兴趣与信心。
重 点 与 难 点 重点:等腰三角形相关知识正确理解与灵活运用。难点:解决问题方法的提练。
教学策略 教 法 选 择 探索发现、归纳总结
学 法 引 导 动手实践、合作交流
课堂组织形式 师生互动,提出问题,解决问题。
教具和多媒体应用 课件
教学过程 一、活动1:深思熟虑 1. 通过问题的形式,对“等腰三角形的特征和识别”进行回顾和归纳。如图,在等腰三角形ABC中,AB=AC. (1)根据等腰三角形的性质,能得出什么结论?(2)请你添加一个条件,使得△ABC成为等边三角形. (3)作底边BC的中线AD,你又能得出什么结论?并请你说明理由.(4)如果AC=5,BC=6,求AD的长.2.提示等腰三角形与直角三角形的联系等腰 底边上的高(或中线) 直角三角形 三角形 用问题的形式让学生回忆等腰三角形的性质、判定.了解学生对本单元知识的储备情况.建立数学图形、知识间的联系.向学生渗透转化的数学思想。
1.在△ABC中,已知AB=AC,AD是中线,(1)若∠B=70°, 则∠BDA= , ∠DAC= (2)若∠BAD=30°,BC=8cm,则AB长为 , 该三角形有 条对称轴. 培养运用基本数学知识解决问题的能力。
活动2:知识演练 第1题图 第3题图2. 已知,在等腰△ABC中,(1)若∠A=70°,则∠B=____度(2)若AB=5,BC=9,则它的周长为___. 3. 如图, 在△ABC中,AB=AC, ∠ABC和∠ACB的平分线交于点P,过点P作DE∥BC,分别交AB、AC于点D、E,则图中等腰三角形的个数是( ) A.5个 B.4个 C.3个 D.2个 若连接AP,则AP与BC有什么关系? 通过训练,培养学生的发散思维。通过变式训练,渗透分类数学思想。
活动3:知识小结 等腰三角形1.定义:有两边相等的三角形叫做等腰三角形.2.性质:(1)等腰三角形的两底角相等(等边对等角)(2)等腰三角形顶角的平分线、底边上的高、底边上的中线重合。(三线合一)(3)等腰三角形是轴对称图形(4)等边三角形三边相等,三角相等,且每一个角为60° 3.判定:(1)定义:(2)如果一个三角形有两角相等,那么这两个角所对的边也相等(等角对等边)(3)有一个角为60°的等腰三角形是等边三角形(4)三个角都相等的三角形是等边三角形4.常用结论:(1)30°所对的直角边等于斜边的一半(2)边长为a的等边三角形的面积为: 通过归纳让学生构筑知识体系,便于学生能综合运用知识。
活动4:仔细辨析 下列说法是否正确?若不正确请更正1.等腰三角形的角平分线、中线、高相互重合2.等腰三角形是轴对称图形,其对称轴是顶角的平分线.3.等腰三角形只有一条对称轴 通过辨析,培养学生语言的严谨性、思维的灵活性
教学过程 活动5:例题分析 例1、如图,OA平分∠BAC,∠1=∠2, 求证:△ABC是等腰三角形.(06南充)第1题图 第2题图例2.等腰△ABC的底边BC=8cm,腰AB=5cm,一动点P在底边上从B点开始向终点C以0.25cm/s的速度运动,点P运动多少时间时,PA与腰垂直 例3.如图,P是正△ABC内的一点,且PA=8,PB=6PC=10,若将△PAC绕点A逆时针旋转后,得到△P1AB,求PP1的长(06青岛) 通过引导学生分析解决问题,让学生掌握策略知识,提高学生综合运用知识解决问题的能力。
活动6:巩固提高 1.如图,沿AC方向开山修渠,为了加快施工进度,要在小山的另一边同时施工.从AC上的一点B取∠ABD=135°,BD=520米,∠D=45°,如果要使A、C、E成一直线,那么开挖点E离D的距离为_______米 (结果保留根号)2.如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE相交于点M、N,有如下结论:①△ACE≌△DBC;②CM=CN;③AC=DN.其中正确结论的个数是( )A.3个 B.2个,C.1个 D.0个(06天津) 培养学生运用数学知识解决问题的能力引导学生重视课本,能从课本的典型例题、习题、图形中发现隐藏的结论。
活动6:巩固提高 3.如图,在△ABC中,AB=AC,∠BAD=20,
且AE=AD,则∠CDE=( ). 4.如图,D、E为AB、AC的中点,将△ABC沿线段DE折叠,使点A落在点F处,若∠B=50°,则DB与DF的关系是( )A.DB>DF B.DB=DF C.DB活动7:课堂小结 谈感受:质疑:教师针对性指导;
活动8:布置作业 《能力检测》第129页—130页内容。
教学后记
孝南区书院中学
邓志军
2007年4月18日
PAGE
12
教 学 设 计
课 题: <<等腰三角形>> 复 习 设计意图
教学目标 知 识 与 技 能 通过“等腰三角形的特征与识别”的复习,使同学们能灵活运用相关知识解决数学以及日常生活中的问题。
过 程 与 方 法 通过观察、猜想、归纳、推理以及变式训练,培养学生的发散思维能力,增强学生的分析问题能力和创新意识;渗透分类数学思想。
情 感、态 度与 价 值 观 通过探索问题的各种情况,让学生体验成功的快乐增强学习数学的兴趣与信心。
重 点 与 难 点 重点:等腰三角形相关知识正确理解与灵活运用。难点:解决问题方法的提练。
教学策略 教 法 选 择 探索发现、归纳总结
学 法 引 导 动手实践、合作交流
课堂组织形式 师生互动,提出问题,解决问题。
教具和多媒体应用 课件
教学过程 一、活动1:深思熟虑 1. 通过问题的形式,对“等腰三角形的特征和识别”进行回顾和归纳。如图,在等腰三角形ABC中,AB=AC. (1)根据等腰三角形的性质,能得出什么结论?(2)请你添加一个条件,使得△ABC成为等边三角形. (3)作底边BC的中线AD,你又能得出什么结论?并请你说明理由.(4)如果AC=5,BC=6,求AD的长.2.提示等腰三角形与直角三角形的联系等腰 底边上的高(或中线) 直角三角形 三角形 用问题的形式让学生回忆等腰三角形的性质、判定.了解学生对本单元知识的储备情况.建立数学图形、知识间的联系.向学生渗透转化的数学思想。
1.在△ABC中,已知AB=AC,AD是中线,(1)若∠B=70°, 则∠BDA= , ∠DAC= (2)若∠BAD=30°,BC=8cm,则AB长为 , 该三角形有 条对称轴. 培养运用基本数学知识解决问题的能力。
活动2:知识演练 第1题图 第3题图2. 已知,在等腰△ABC中,(1)若∠A=70°,则∠B=____度(2)若AB=5,BC=9,则它的周长为___. 3. 如图, 在△ABC中,AB=AC, ∠ABC和∠ACB的平分线交于点P,过点P作DE∥BC,分别交AB、AC于点D、E,则图中等腰三角形的个数是( ) A.5个 B.4个 C.3个 D.2个 若连接AP,则AP与BC有什么关系? 通过训练,培养学生的发散思维。通过变式训练,渗透分类数学思想。
活动3:知识小结 等腰三角形1.定义:有两边相等的三角形叫做等腰三角形.2.性质:(1)等腰三角形的两底角相等(等边对等角)(2)等腰三角形顶角的平分线、底边上的高、底边上的中线重合。(三线合一)(3)等腰三角形是轴对称图形(4)等边三角形三边相等,三角相等,且每一个角为60° 3.判定:(1)定义:(2)如果一个三角形有两角相等,那么这两个角所对的边也相等(等角对等边)(3)有一个角为60°的等腰三角形是等边三角形(4)三个角都相等的三角形是等边三角形4.常用结论:(1)30°所对的直角边等于斜边的一半(2)边长为a的等边三角形的面积为: 通过归纳让学生构筑知识体系,便于学生能综合运用知识。
活动4:仔细辨析 下列说法是否正确?若不正确请更正1.等腰三角形的角平分线、中线、高相互重合2.等腰三角形是轴对称图形,其对称轴是顶角的平分线.3.等腰三角形只有一条对称轴 通过辨析,培养学生语言的严谨性、思维的灵活性
教学过程 活动5:例题分析 例1、如图,OA平分∠BAC,∠1=∠2, 求证:△ABC是等腰三角形.(06南充)第1题图 第2题图例2.等腰△ABC的底边BC=8cm,腰AB=5cm,一动点P在底边上从B点开始向终点C以0.25cm/s的速度运动,点P运动多少时间时,PA与腰垂直 例3.如图,P是正△ABC内的一点,且PA=8,PB=6PC=10,若将△PAC绕点A逆时针旋转后,得到△P1AB,求PP1的长(06青岛) 通过引导学生分析解决问题,让学生掌握策略知识,提高学生综合运用知识解决问题的能力。
活动6:巩固提高 1.如图,沿AC方向开山修渠,为了加快施工进度,要在小山的另一边同时施工.从AC上的一点B取∠ABD=135°,BD=520米,∠D=45°,如果要使A、C、E成一直线,那么开挖点E离D的距离为_______米 (结果保留根号)2.如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE相交于点M、N,有如下结论:①△ACE≌△DBC;②CM=CN;③AC=DN.其中正确结论的个数是( )A.3个 B.2个,C.1个 D.0个(06天津) 培养学生运用数学知识解决问题的能力引导学生重视课本,能从课本的典型例题、习题、图形中发现隐藏的结论。
活动6:巩固提高 3.如图,在△ABC中,AB=AC,∠BAD=20,
且AE=AD,则∠CDE=( ). 4.如图,D、E为AB、AC的中点,将△ABC沿线段DE折叠,使点A落在点F处,若∠B=50°,则DB与DF的关系是( )A.DB>DF B.DB=DF C.DB
活动8:布置作业 《能力检测》第129页—130页内容。
教学后记
孝南区书院中学
邓志军
2007年4月18日
PAGE
12
