青岛版 2021-2022学年山东省东营市经济开发区五年级(上)期末数学试卷 (含答案)
文档属性
| 名称 | 青岛版 2021-2022学年山东省东营市经济开发区五年级(上)期末数学试卷 (含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 347.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-18 20:28:43 | ||
图片预览



文档简介
2021-2022学年山东省东营市经济开发区五年级(上)期末数学试卷
一、填一填。(共26分,第8题4分,其余每空1分)
1.(5分)
405cm3= dm3 7.8L= cm3
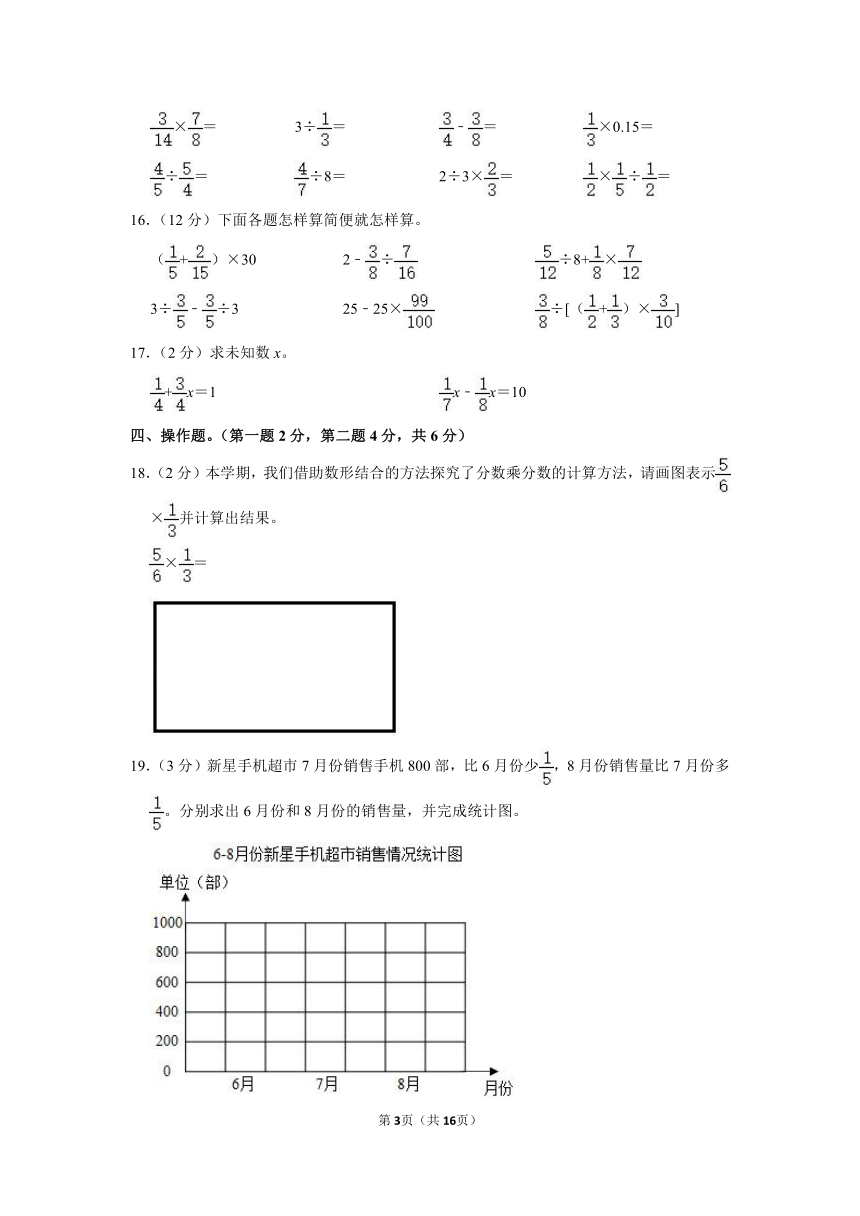
m3= dm3 1020mL= L mL
2.(4分)在横线上填上合适的单位名称。
一盒牛奶的容积约是250 一个纯蓝墨水瓶的体积约是50
一台洗衣机的容积约是40 一根火腿肠的质量约是30
3.(5分)在横线上填上“>”“<”或“=”。
×1 1÷ ×
÷ ÷ ×
4.(3分) ÷10== :15= (填小数)。
5.(2分)把0.4:化成最简整数比是 ,它的比值是 .
6.(2分)把m长的木料平均锯成6段,每段长 m,每段占全长的 .
7.(2分)把两个长3厘米,宽2厘米,高1厘米的小长方体拼成一个大长方体,如图,拼成的长方体的体积是 立方厘米,表面积是 平方厘米。
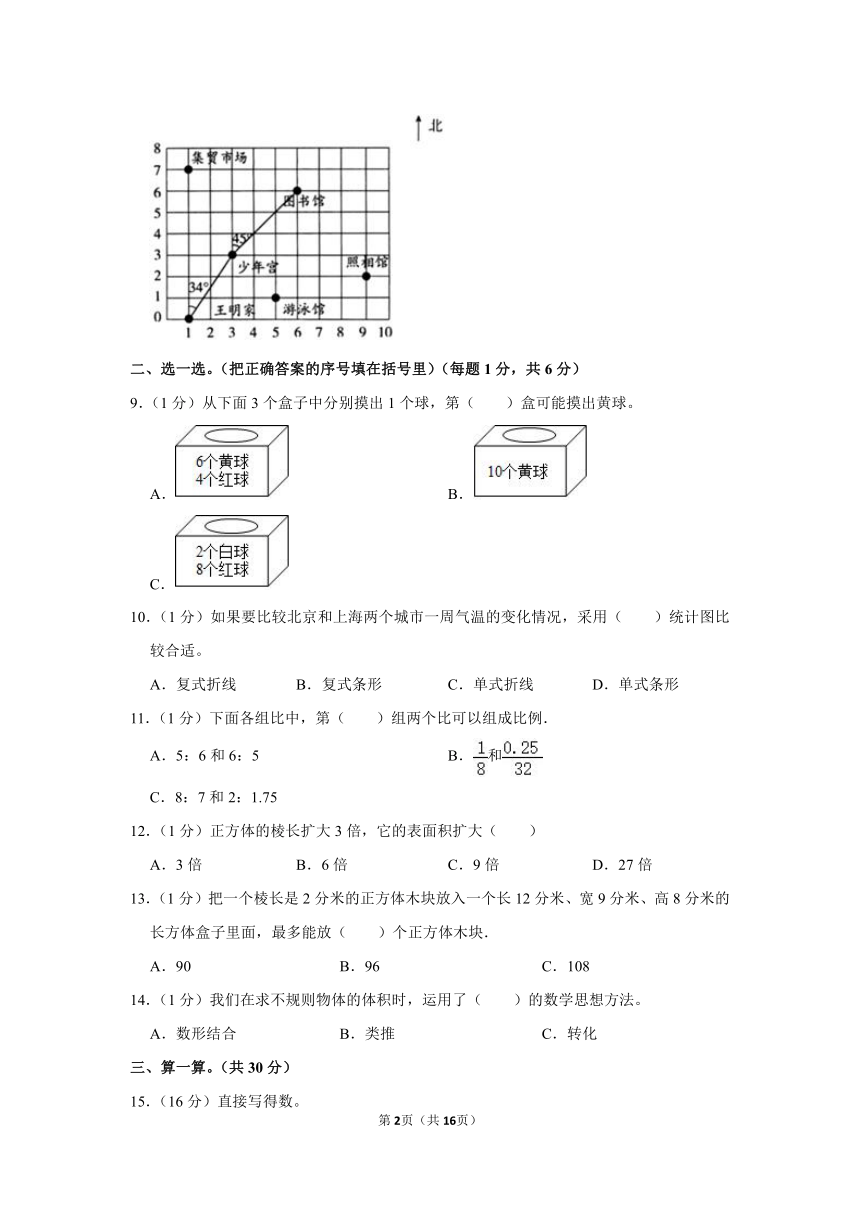
8.(4分)如图是王明家位置的平面图。
(1)游泳馆和集贸市场的位置用数对表示分别表示为 和 。
(2)王明从家出发,向 偏 方向走到少年宫,再向 偏 方向走到图书馆。
二、选一选。(把正确答案的序号填在括号里)(每题1分,共6分)
9.(1分)从下面3个盒子中分别摸出1个球,第( )盒可能摸出黄球。
A. B.
C.
10.(1分)如果要比较北京和上海两个城市一周气温的变化情况,采用( )统计图比较合适。
A.复式折线 B.复式条形 C.单式折线 D.单式条形
11.(1分)下面各组比中,第( )组两个比可以组成比例.
A.5:6和6:5 B.和
C.8:7和2:1.75
12.(1分)正方体的棱长扩大3倍,它的表面积扩大( )
A.3倍 B.6倍 C.9倍 D.27倍
13.(1分)把一个棱长是2分米的正方体木块放入一个长12分米、宽9分米、高8分米的长方体盒子里面,最多能放( )个正方体木块.
A.90 B.96 C.108
14.(1分)我们在求不规则物体的体积时,运用了( )的数学思想方法。
A.数形结合 B.类推 C.转化
三、算一算。(共30分)
15.(16分)直接写得数。
×= 3÷= ﹣= ×0.15=
÷= ÷8= 2÷3×= ×÷=
16.(12分)下面各题怎样算简便就怎样算。
(+)×30 2﹣÷ ÷8+×
3÷﹣÷3 25﹣25× ÷[(+)×]
17.(2分)求未知数x。
+x=1 x﹣x=10
四、操作题。(第一题2分,第二题4分,共6分)
18.(2分)本学期,我们借助数形结合的方法探究了分数乘分数的计算方法,请画图表示×并计算出结果。
×=
19.(3分)新星手机超市7月份销售手机800部,比6月份少,8月份销售量比7月份多。分别求出6月份和8月份的销售量,并完成统计图。
五、解决问题。(每题4分,共32分)
20.(4分)一间教室长9米,宽7米,高3米.要粉刷教室的屋顶和墙壁(除去门窗和黑板的面积29.6平方米),粉刷面积是多少平方米?如果平均每平方米用0.2千克涂料,至少需要多少千克涂料?
21.(4分)一节长3米的长方体通风管,横截面是一个边长0.5米的正方形。做1节这样的通风管至少需要铁皮多少平方米?
22.(4分)一个直角三角形,两个锐角的度数比是1:2,这个直角三角形中最大的锐角是多少度?
23.(4分)做一长方体形状的无盖的玻璃鱼缸,长110厘米,宽60厘米,高50厘米,做这样一个玻璃鱼缸一共用多少平方厘米的玻璃?
24.(4分)阳光小学五年级有270人,其中女生人数是男生的.男生有多少人?
25.(4分)水结成冰后,体积增加,现在有5升水,结冰后体积是多少立方分米?
26.(4分)北京到青岛的铁路长约900千米,一列火车4小时行驶了全程的.照这样计算,从北京到青岛大约需几小时?
27.(4分)有一个长方体鱼缸(如图),放进去一块珊瑚石,水面升高了5厘米,这块珊瑚石的体积是多少?
2021-2022学年山东省东营市经济开发区五年级(上)期末数学试卷
参考答案与试题解析
一、填一填。(共26分,第8题4分,其余每空1分)
1.(5分)
405cm3= 0.405 dm3 7.8L= 7800 cm3
m3= 750 dm3 1020mL= 1 L 20 mL
【解答】解:
405cm3=0.405dm3 7.8L=7800cm3
m3=750dm3 1020mL=1L20mL
故答案为:0.405;7800;750;1,20。
【点评】立方米、立方分米(升)、立方厘米(毫升)相邻单位之间的进率是1000,由高级单位化低级单位乘进率,反之除以进率。
2.(4分)在横线上填上合适的单位名称。
一盒牛奶的容积约是250 毫升 一个纯蓝墨水瓶的体积约是50 毫升
一台洗衣机的容积约是40 升 一根火腿肠的质量约是30 克
【解答】解:
一盒牛奶的容积约是250毫升 一个纯蓝墨水瓶的体积约是50毫升
一台洗衣机的容积约是40升 一根火腿肠的质量约是30克
故答案为:毫升,毫升,升,克。
【点评】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活地选择。
3.(5分)在横线上填上“>”“<”或“=”。
×1 < 1÷ × <
÷ > ÷ > ×
【解答】解:×1=
1÷=
因为
所以×1<1÷
因为
所以×<
因为
所以÷>
因为<1
所以÷,×
所以÷>×
×1<1÷ ×<
÷> ÷>×
故答案为:<,<,>,>。
【点评】熟练掌握积的变化规律和商的变化规律是解题的关键。
4.(3分) 12 ÷10== 18 :15= 1.2 (填小数)。
【解答】解:12÷10==18:15=1.2。
故答案为:12,18,1.2。
【点评】此题主要是考查除法、小数、分数、比之间的关系及转化。利用它们之间的关系和性质进行转化即可。
5.(2分)把0.4:化成最简整数比是 2:3 ,它的比值是 .
【解答】解:(1)0.4:,
=(0.4×5):(×5),
=2:3;
(2)0.4:,
=2:3,
=2÷3,
=.
故答案为:2:3,.
【点评】此题考查化简比和求比值的方法,要注意区分:化简比的结果是一个比,它的前项和后项都是整数,并且是互质数;而求比值的结果是一个数,可以是整数、小数或分数.
6.(2分)把m长的木料平均锯成6段,每段长 m,每段占全长的 .
【解答】解:(1)÷6=(米);
答:每段是米.
(2)1;
答:每段占全长的.
故答案为:;.
【点评】解决此题关键是弄清求得是分率还是具体的数量,求分率平均分的是单位“1”;求具体的数量平均分的是具体的数量,要注意:分率不能带单位名称,而具体的数量要带单位名称.
7.(2分)把两个长3厘米,宽2厘米,高1厘米的小长方体拼成一个大长方体,如图,拼成的长方体的体积是 12 立方厘米,表面积是 40 平方厘米。
【解答】解:3×2×1×2
=6×2
=12(立方厘米)
2×(6×2+6×1+2×1)
=2×(12+6+2)
=2×20
=40(平方厘米)
答:拼成的长方体的体积是12立方厘米,表面积是40平方厘米。
故答案为:12,40。
【点评】本题考查学生对长方体体积和表面积公式的掌握和运用。
8.(4分)如图是王明家位置的平面图。
(1)游泳馆和集贸市场的位置用数对表示分别表示为 (5,1) 和 (1,7) 。
(2)王明从家出发,向 北 偏 东34° 方向走到少年宫,再向 北 偏 东45° 方向走到图书馆。
【解答】解:(1)游泳馆和集贸市场的位置用数对表示分别表示为(5,1)和(1,7)。
(2)王明从家出发,向北偏东34°方向走到少年宫,再向北偏东45°方向走到图书馆。
故答案为:(5,1);(1,7);北;东34°;北;东45°。
【点评】本题主要考查用数对表示位置时,先表示第几列,再表示第几行。
二、选一选。(把正确答案的序号填在括号里)(每题1分,共6分)
9.(1分)从下面3个盒子中分别摸出1个球,第( )盒可能摸出黄球。
A. B.
C.
【解答】解:可能摸出黄球。
故选:A。
【点评】此题应根据可能性的大小进行分析、解答。
10.(1分)如果要比较北京和上海两个城市一周气温的变化情况,采用( )统计图比较合适。
A.复式折线 B.复式条形 C.单式折线 D.单式条形
【解答】解:如果要比较北京和上海两个城市一周气温的变化情况,采用复式折线统计图比较合适。
故选:A。
【点评】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
11.(1分)下面各组比中,第( )组两个比可以组成比例.
A.5:6和6:5 B.和
C.8:7和2:1.75
【解答】解:A、5:6=,6:5=,比值不相等,构不成比例;
B、=,=,比值不相等,构不成比例;
C、8:7=,2:1.75=,比值相等可构成比例.
故选:C.
【点评】本题考查可构成比例的条件,两个比的比值相等,这两个比可构成比例.
12.(1分)正方体的棱长扩大3倍,它的表面积扩大( )
A.3倍 B.6倍 C.9倍 D.27倍
【解答】解:正方体的棱长扩大3倍,它的表面积就扩大3×3=9倍;
故选:C。
【点评】此题主要根据正方体的表面积的计算方法与积的变化规律解决问题.
13.(1分)把一个棱长是2分米的正方体木块放入一个长12分米、宽9分米、高8分米的长方体盒子里面,最多能放( )个正方体木块.
A.90 B.96 C.108
【解答】解:12÷2=6(个)
9÷2=4(排)…1(分米)
8÷2=4(层)
6×4×4=96(个)
答:最多能放96个正方体木块.
故选:B.
【点评】此题主要考查长方体的体积公式的灵活运用,关键是熟记公式.
14.(1分)我们在求不规则物体的体积时,运用了( )的数学思想方法。
A.数形结合 B.类推 C.转化
【解答】解:我们在求不规则物体的体积时,运用了转化的数学思想方法。
故选:C。
【点评】本题考查求不规则物体的体积的方法。
三、算一算。(共30分)
15.(16分)直接写得数。
×= 3÷= ﹣= ×0.15=
÷= ÷8= 2÷3×= ×÷=
【解答】解:
×= 3÷=9 ﹣= ×0.15=0.05
÷= ÷8= 2÷3×= ×÷=
【点评】本题考查分数加、减、乘、除四则运算,解题关键是熟练掌握分数加减法,乘除法的计算法则,注意计算结果要化成最简分数。
16.(12分)下面各题怎样算简便就怎样算。
(+)×30 2﹣÷ ÷8+×
3÷﹣÷3 25﹣25× ÷[(+)×]
【解答】解:(1)(+)×30
=×30+×30
=6+4
=10
(2)2﹣÷
=2﹣
=1
(3)÷8+×
=×(+)
=×1
=
(4)3÷﹣÷3
=5﹣
=4
(5)25﹣25×
=25×(1﹣)
=25×
=0.25
(6)÷[(+)×]
=÷[×]
=÷
=
【点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
17.(2分)求未知数x。
+x=1 x﹣x=10
【解答】解:(1)+x=1
+x﹣=1﹣
x=
x=
x=1
(2)x﹣x=10
x=10
56×x=10×56
x=560
【点评】熟练掌握等式的基本性质是解题的关键。
四、操作题。(第一题2分,第二题4分,共6分)
18.(2分)本学期,我们借助数形结合的方法探究了分数乘分数的计算方法,请画图表示×并计算出结果。
×=
【解答】解:
【点评】本题考查分数乘法的计算,解题关键是理解并掌握运用画图的方法表示分数乘分数的计算结果。
19.(3分)新星手机超市7月份销售手机800部,比6月份少,8月份销售量比7月份多。分别求出6月份和8月份的销售量,并完成统计图。
【解答】解:6月份:800÷(1﹣)=1000(部)
8月份:800×(1+)=960(部)
统计图如下:
答:6月份销售1000部,8月份销售960部。
【点评】解答本题的关键是求出6月份和8月份的销售量。
五、解决问题。(每题4分,共32分)
20.(4分)一间教室长9米,宽7米,高3米.要粉刷教室的屋顶和墙壁(除去门窗和黑板的面积29.6平方米),粉刷面积是多少平方米?如果平均每平方米用0.2千克涂料,至少需要多少千克涂料?
【解答】解:9×7+(9×3+7×3)×2﹣29.6
=63+(27+21)×2﹣29.6
=63+96﹣29.6
=159﹣29.6
=129.4(平方米)
129.4×0.2=25.88(千克)
答:粉刷面积是129.4平方米,至少需要25.88千克涂料.
【点评】本题主要考查了学生对长方体表面积计算公式的应用,在计算时一定要注意需要涂的是哪几个面.
21.(4分)一节长3米的长方体通风管,横截面是一个边长0.5米的正方形。做1节这样的通风管至少需要铁皮多少平方米?
【解答】解:0.5×4×3
=2×3
=6(平方米)
答:做1节这样的通风管至少需要铁皮6平方米。
【点评】解答有关长方体计算的实际问题,一定要搞清所求的是什么,再进一步选择合理的计算方法进行计算解答问题。
22.(4分)一个直角三角形,两个锐角的度数比是1:2,这个直角三角形中最大的锐角是多少度?
【解答】解:90×
=90×
=60(度)
答:这个直角三角形中最大的锐角是60度。
【点评】把比转化成分数,再根据锐角三角形的特征及按比例分配问题即可解答。
23.(4分)做一长方体形状的无盖的玻璃鱼缸,长110厘米,宽60厘米,高50厘米,做这样一个玻璃鱼缸一共用多少平方厘米的玻璃?
【解答】解:110×60+2×110×50+2×60×50
=6600+11000+6000
=23600(平方厘米)
答:做这样一个玻璃鱼缸一共用23600平方厘米的玻璃。
【点评】解答有关长方体计算的实际问题,一定要搞清所求的是什么,再进一步选择合理的计算方法进行计算解答问题。
24.(4分)阳光小学五年级有270人,其中女生人数是男生的.男生有多少人?
【解答】解:270÷(1+)
=270÷
=150(人)
答:男生有150人.
【点评】解答此题关键找出单位“1”,确定具体数量对应的分率,解答依据是:已知单位“1”的几分之几是多少,求单位“1”用除法求解.
25.(4分)水结成冰后,体积增加,现在有5升水,结冰后体积是多少立方分米?
【解答】解:5×(1+),
=5×,
=5.5(立方米),
答:结冰后的体积是5.5立方分米.
【点评】将水的体积当作单位“1”,首先求出冰占水的体积的分率是完成本题的关键.
26.(4分)北京到青岛的铁路长约900千米,一列火车4小时行驶了全程的.照这样计算,从北京到青岛大约需几小时?
【解答】解:4÷=4×3=12(小时);
答:从北京到青岛大约需12小时.
【点评】此题也可这样理解:4小时行驶了全程的,每小时行÷4=,那么每小时行900×=75(千米),行完全程需要的时间为900÷75=12(小时),综合算式:900÷[900×(÷4)].
27.(4分)有一个长方体鱼缸(如图),放进去一块珊瑚石,水面升高了5厘米,这块珊瑚石的体积是多少?
【解答】解:5厘米=0.5分米
9×6×0.5
=54×0.5
=27(立方分米)
答:这块珊瑚石的体积是27立方分米.
【点评】解答本题的关键是理解珊瑚石的体积即上升水的体积.
第1页(共1页)
一、填一填。(共26分,第8题4分,其余每空1分)
1.(5分)
405cm3= dm3 7.8L= cm3
m3= dm3 1020mL= L mL
2.(4分)在横线上填上合适的单位名称。
一盒牛奶的容积约是250 一个纯蓝墨水瓶的体积约是50
一台洗衣机的容积约是40 一根火腿肠的质量约是30
3.(5分)在横线上填上“>”“<”或“=”。
×1 1÷ ×
÷ ÷ ×
4.(3分) ÷10== :15= (填小数)。
5.(2分)把0.4:化成最简整数比是 ,它的比值是 .
6.(2分)把m长的木料平均锯成6段,每段长 m,每段占全长的 .
7.(2分)把两个长3厘米,宽2厘米,高1厘米的小长方体拼成一个大长方体,如图,拼成的长方体的体积是 立方厘米,表面积是 平方厘米。
8.(4分)如图是王明家位置的平面图。
(1)游泳馆和集贸市场的位置用数对表示分别表示为 和 。
(2)王明从家出发,向 偏 方向走到少年宫,再向 偏 方向走到图书馆。
二、选一选。(把正确答案的序号填在括号里)(每题1分,共6分)
9.(1分)从下面3个盒子中分别摸出1个球,第( )盒可能摸出黄球。
A. B.
C.
10.(1分)如果要比较北京和上海两个城市一周气温的变化情况,采用( )统计图比较合适。
A.复式折线 B.复式条形 C.单式折线 D.单式条形
11.(1分)下面各组比中,第( )组两个比可以组成比例.
A.5:6和6:5 B.和
C.8:7和2:1.75
12.(1分)正方体的棱长扩大3倍,它的表面积扩大( )
A.3倍 B.6倍 C.9倍 D.27倍
13.(1分)把一个棱长是2分米的正方体木块放入一个长12分米、宽9分米、高8分米的长方体盒子里面,最多能放( )个正方体木块.
A.90 B.96 C.108
14.(1分)我们在求不规则物体的体积时,运用了( )的数学思想方法。
A.数形结合 B.类推 C.转化
三、算一算。(共30分)
15.(16分)直接写得数。
×= 3÷= ﹣= ×0.15=
÷= ÷8= 2÷3×= ×÷=
16.(12分)下面各题怎样算简便就怎样算。
(+)×30 2﹣÷ ÷8+×
3÷﹣÷3 25﹣25× ÷[(+)×]
17.(2分)求未知数x。
+x=1 x﹣x=10
四、操作题。(第一题2分,第二题4分,共6分)
18.(2分)本学期,我们借助数形结合的方法探究了分数乘分数的计算方法,请画图表示×并计算出结果。
×=
19.(3分)新星手机超市7月份销售手机800部,比6月份少,8月份销售量比7月份多。分别求出6月份和8月份的销售量,并完成统计图。
五、解决问题。(每题4分,共32分)
20.(4分)一间教室长9米,宽7米,高3米.要粉刷教室的屋顶和墙壁(除去门窗和黑板的面积29.6平方米),粉刷面积是多少平方米?如果平均每平方米用0.2千克涂料,至少需要多少千克涂料?
21.(4分)一节长3米的长方体通风管,横截面是一个边长0.5米的正方形。做1节这样的通风管至少需要铁皮多少平方米?
22.(4分)一个直角三角形,两个锐角的度数比是1:2,这个直角三角形中最大的锐角是多少度?
23.(4分)做一长方体形状的无盖的玻璃鱼缸,长110厘米,宽60厘米,高50厘米,做这样一个玻璃鱼缸一共用多少平方厘米的玻璃?
24.(4分)阳光小学五年级有270人,其中女生人数是男生的.男生有多少人?
25.(4分)水结成冰后,体积增加,现在有5升水,结冰后体积是多少立方分米?
26.(4分)北京到青岛的铁路长约900千米,一列火车4小时行驶了全程的.照这样计算,从北京到青岛大约需几小时?
27.(4分)有一个长方体鱼缸(如图),放进去一块珊瑚石,水面升高了5厘米,这块珊瑚石的体积是多少?
2021-2022学年山东省东营市经济开发区五年级(上)期末数学试卷
参考答案与试题解析
一、填一填。(共26分,第8题4分,其余每空1分)
1.(5分)
405cm3= 0.405 dm3 7.8L= 7800 cm3
m3= 750 dm3 1020mL= 1 L 20 mL
【解答】解:
405cm3=0.405dm3 7.8L=7800cm3
m3=750dm3 1020mL=1L20mL
故答案为:0.405;7800;750;1,20。
【点评】立方米、立方分米(升)、立方厘米(毫升)相邻单位之间的进率是1000,由高级单位化低级单位乘进率,反之除以进率。
2.(4分)在横线上填上合适的单位名称。
一盒牛奶的容积约是250 毫升 一个纯蓝墨水瓶的体积约是50 毫升
一台洗衣机的容积约是40 升 一根火腿肠的质量约是30 克
【解答】解:
一盒牛奶的容积约是250毫升 一个纯蓝墨水瓶的体积约是50毫升
一台洗衣机的容积约是40升 一根火腿肠的质量约是30克
故答案为:毫升,毫升,升,克。
【点评】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活地选择。
3.(5分)在横线上填上“>”“<”或“=”。
×1 < 1÷ × <
÷ > ÷ > ×
【解答】解:×1=
1÷=
因为
所以×1<1÷
因为
所以×<
因为
所以÷>
因为<1
所以÷,×
所以÷>×
×1<1÷ ×<
÷> ÷>×
故答案为:<,<,>,>。
【点评】熟练掌握积的变化规律和商的变化规律是解题的关键。
4.(3分) 12 ÷10== 18 :15= 1.2 (填小数)。
【解答】解:12÷10==18:15=1.2。
故答案为:12,18,1.2。
【点评】此题主要是考查除法、小数、分数、比之间的关系及转化。利用它们之间的关系和性质进行转化即可。
5.(2分)把0.4:化成最简整数比是 2:3 ,它的比值是 .
【解答】解:(1)0.4:,
=(0.4×5):(×5),
=2:3;
(2)0.4:,
=2:3,
=2÷3,
=.
故答案为:2:3,.
【点评】此题考查化简比和求比值的方法,要注意区分:化简比的结果是一个比,它的前项和后项都是整数,并且是互质数;而求比值的结果是一个数,可以是整数、小数或分数.
6.(2分)把m长的木料平均锯成6段,每段长 m,每段占全长的 .
【解答】解:(1)÷6=(米);
答:每段是米.
(2)1;
答:每段占全长的.
故答案为:;.
【点评】解决此题关键是弄清求得是分率还是具体的数量,求分率平均分的是单位“1”;求具体的数量平均分的是具体的数量,要注意:分率不能带单位名称,而具体的数量要带单位名称.
7.(2分)把两个长3厘米,宽2厘米,高1厘米的小长方体拼成一个大长方体,如图,拼成的长方体的体积是 12 立方厘米,表面积是 40 平方厘米。
【解答】解:3×2×1×2
=6×2
=12(立方厘米)
2×(6×2+6×1+2×1)
=2×(12+6+2)
=2×20
=40(平方厘米)
答:拼成的长方体的体积是12立方厘米,表面积是40平方厘米。
故答案为:12,40。
【点评】本题考查学生对长方体体积和表面积公式的掌握和运用。
8.(4分)如图是王明家位置的平面图。
(1)游泳馆和集贸市场的位置用数对表示分别表示为 (5,1) 和 (1,7) 。
(2)王明从家出发,向 北 偏 东34° 方向走到少年宫,再向 北 偏 东45° 方向走到图书馆。
【解答】解:(1)游泳馆和集贸市场的位置用数对表示分别表示为(5,1)和(1,7)。
(2)王明从家出发,向北偏东34°方向走到少年宫,再向北偏东45°方向走到图书馆。
故答案为:(5,1);(1,7);北;东34°;北;东45°。
【点评】本题主要考查用数对表示位置时,先表示第几列,再表示第几行。
二、选一选。(把正确答案的序号填在括号里)(每题1分,共6分)
9.(1分)从下面3个盒子中分别摸出1个球,第( )盒可能摸出黄球。
A. B.
C.
【解答】解:可能摸出黄球。
故选:A。
【点评】此题应根据可能性的大小进行分析、解答。
10.(1分)如果要比较北京和上海两个城市一周气温的变化情况,采用( )统计图比较合适。
A.复式折线 B.复式条形 C.单式折线 D.单式条形
【解答】解:如果要比较北京和上海两个城市一周气温的变化情况,采用复式折线统计图比较合适。
故选:A。
【点评】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
11.(1分)下面各组比中,第( )组两个比可以组成比例.
A.5:6和6:5 B.和
C.8:7和2:1.75
【解答】解:A、5:6=,6:5=,比值不相等,构不成比例;
B、=,=,比值不相等,构不成比例;
C、8:7=,2:1.75=,比值相等可构成比例.
故选:C.
【点评】本题考查可构成比例的条件,两个比的比值相等,这两个比可构成比例.
12.(1分)正方体的棱长扩大3倍,它的表面积扩大( )
A.3倍 B.6倍 C.9倍 D.27倍
【解答】解:正方体的棱长扩大3倍,它的表面积就扩大3×3=9倍;
故选:C。
【点评】此题主要根据正方体的表面积的计算方法与积的变化规律解决问题.
13.(1分)把一个棱长是2分米的正方体木块放入一个长12分米、宽9分米、高8分米的长方体盒子里面,最多能放( )个正方体木块.
A.90 B.96 C.108
【解答】解:12÷2=6(个)
9÷2=4(排)…1(分米)
8÷2=4(层)
6×4×4=96(个)
答:最多能放96个正方体木块.
故选:B.
【点评】此题主要考查长方体的体积公式的灵活运用,关键是熟记公式.
14.(1分)我们在求不规则物体的体积时,运用了( )的数学思想方法。
A.数形结合 B.类推 C.转化
【解答】解:我们在求不规则物体的体积时,运用了转化的数学思想方法。
故选:C。
【点评】本题考查求不规则物体的体积的方法。
三、算一算。(共30分)
15.(16分)直接写得数。
×= 3÷= ﹣= ×0.15=
÷= ÷8= 2÷3×= ×÷=
【解答】解:
×= 3÷=9 ﹣= ×0.15=0.05
÷= ÷8= 2÷3×= ×÷=
【点评】本题考查分数加、减、乘、除四则运算,解题关键是熟练掌握分数加减法,乘除法的计算法则,注意计算结果要化成最简分数。
16.(12分)下面各题怎样算简便就怎样算。
(+)×30 2﹣÷ ÷8+×
3÷﹣÷3 25﹣25× ÷[(+)×]
【解答】解:(1)(+)×30
=×30+×30
=6+4
=10
(2)2﹣÷
=2﹣
=1
(3)÷8+×
=×(+)
=×1
=
(4)3÷﹣÷3
=5﹣
=4
(5)25﹣25×
=25×(1﹣)
=25×
=0.25
(6)÷[(+)×]
=÷[×]
=÷
=
【点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
17.(2分)求未知数x。
+x=1 x﹣x=10
【解答】解:(1)+x=1
+x﹣=1﹣
x=
x=
x=1
(2)x﹣x=10
x=10
56×x=10×56
x=560
【点评】熟练掌握等式的基本性质是解题的关键。
四、操作题。(第一题2分,第二题4分,共6分)
18.(2分)本学期,我们借助数形结合的方法探究了分数乘分数的计算方法,请画图表示×并计算出结果。
×=
【解答】解:
【点评】本题考查分数乘法的计算,解题关键是理解并掌握运用画图的方法表示分数乘分数的计算结果。
19.(3分)新星手机超市7月份销售手机800部,比6月份少,8月份销售量比7月份多。分别求出6月份和8月份的销售量,并完成统计图。
【解答】解:6月份:800÷(1﹣)=1000(部)
8月份:800×(1+)=960(部)
统计图如下:
答:6月份销售1000部,8月份销售960部。
【点评】解答本题的关键是求出6月份和8月份的销售量。
五、解决问题。(每题4分,共32分)
20.(4分)一间教室长9米,宽7米,高3米.要粉刷教室的屋顶和墙壁(除去门窗和黑板的面积29.6平方米),粉刷面积是多少平方米?如果平均每平方米用0.2千克涂料,至少需要多少千克涂料?
【解答】解:9×7+(9×3+7×3)×2﹣29.6
=63+(27+21)×2﹣29.6
=63+96﹣29.6
=159﹣29.6
=129.4(平方米)
129.4×0.2=25.88(千克)
答:粉刷面积是129.4平方米,至少需要25.88千克涂料.
【点评】本题主要考查了学生对长方体表面积计算公式的应用,在计算时一定要注意需要涂的是哪几个面.
21.(4分)一节长3米的长方体通风管,横截面是一个边长0.5米的正方形。做1节这样的通风管至少需要铁皮多少平方米?
【解答】解:0.5×4×3
=2×3
=6(平方米)
答:做1节这样的通风管至少需要铁皮6平方米。
【点评】解答有关长方体计算的实际问题,一定要搞清所求的是什么,再进一步选择合理的计算方法进行计算解答问题。
22.(4分)一个直角三角形,两个锐角的度数比是1:2,这个直角三角形中最大的锐角是多少度?
【解答】解:90×
=90×
=60(度)
答:这个直角三角形中最大的锐角是60度。
【点评】把比转化成分数,再根据锐角三角形的特征及按比例分配问题即可解答。
23.(4分)做一长方体形状的无盖的玻璃鱼缸,长110厘米,宽60厘米,高50厘米,做这样一个玻璃鱼缸一共用多少平方厘米的玻璃?
【解答】解:110×60+2×110×50+2×60×50
=6600+11000+6000
=23600(平方厘米)
答:做这样一个玻璃鱼缸一共用23600平方厘米的玻璃。
【点评】解答有关长方体计算的实际问题,一定要搞清所求的是什么,再进一步选择合理的计算方法进行计算解答问题。
24.(4分)阳光小学五年级有270人,其中女生人数是男生的.男生有多少人?
【解答】解:270÷(1+)
=270÷
=150(人)
答:男生有150人.
【点评】解答此题关键找出单位“1”,确定具体数量对应的分率,解答依据是:已知单位“1”的几分之几是多少,求单位“1”用除法求解.
25.(4分)水结成冰后,体积增加,现在有5升水,结冰后体积是多少立方分米?
【解答】解:5×(1+),
=5×,
=5.5(立方米),
答:结冰后的体积是5.5立方分米.
【点评】将水的体积当作单位“1”,首先求出冰占水的体积的分率是完成本题的关键.
26.(4分)北京到青岛的铁路长约900千米,一列火车4小时行驶了全程的.照这样计算,从北京到青岛大约需几小时?
【解答】解:4÷=4×3=12(小时);
答:从北京到青岛大约需12小时.
【点评】此题也可这样理解:4小时行驶了全程的,每小时行÷4=,那么每小时行900×=75(千米),行完全程需要的时间为900÷75=12(小时),综合算式:900÷[900×(÷4)].
27.(4分)有一个长方体鱼缸(如图),放进去一块珊瑚石,水面升高了5厘米,这块珊瑚石的体积是多少?
【解答】解:5厘米=0.5分米
9×6×0.5
=54×0.5
=27(立方分米)
答:这块珊瑚石的体积是27立方分米.
【点评】解答本题的关键是理解珊瑚石的体积即上升水的体积.
第1页(共1页)
同课章节目录
