2022-2023学年安徽省滁州市定远县永康片八年级(上)期中数学试卷 (含解析)
文档属性
| 名称 | 2022-2023学年安徽省滁州市定远县永康片八年级(上)期中数学试卷 (含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 702.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-19 09:25:00 | ||
图片预览


文档简介
2022-2023学年安徽省滁州市定远县永康片八年级(上)期中数学试卷
一、选择题(本大题共10小题,共40分。在每小题列出的选项中,选出符合题目的一项)
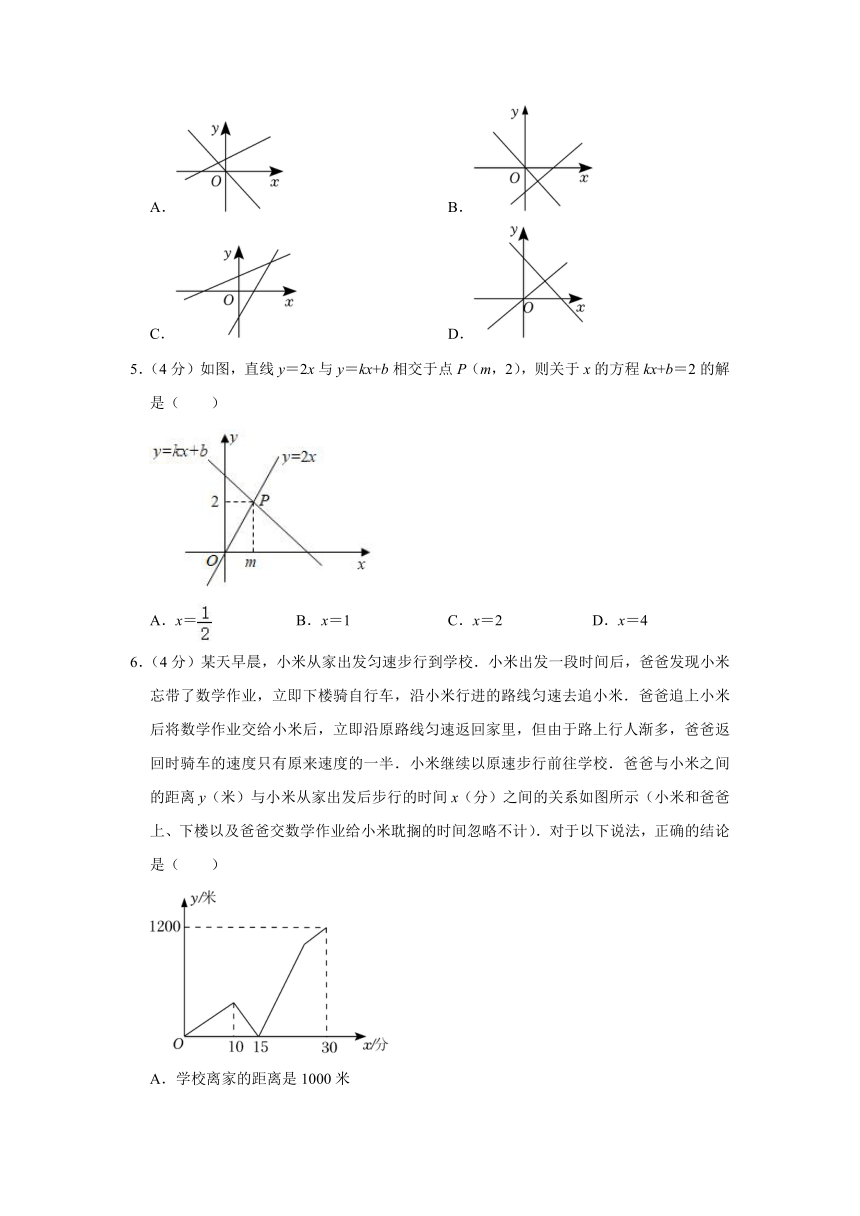
1.(4分)如图,在直角坐标系中,边长为2的等边△OA1A2的一条边OA2在x的正半轴上,O为坐标原点;将△OA1A2沿x轴正方形依此向右移动4个单位,依次得△A3A4A5,△A6A7A8…,则顶点A2019的坐标为( )
A.(2690,0) B.(2692,0) C.(2694,0) D.无法确定
2.(4分)已知函数y=(m+1)x是正比例函数,且图象在第二、四象限内,则m的值是( )
A.2 B.﹣2 C.±2 D.﹣
3.(4分)若一次函数y=kx+b的图象经过第一、二、四象限,则一次函数y=bx+k的图象大致是( )
A. B.
C. D.
4.(4分)一次函数y=kx+b与正比例函数y=kbx(k,b为常数,且kb≠0)在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
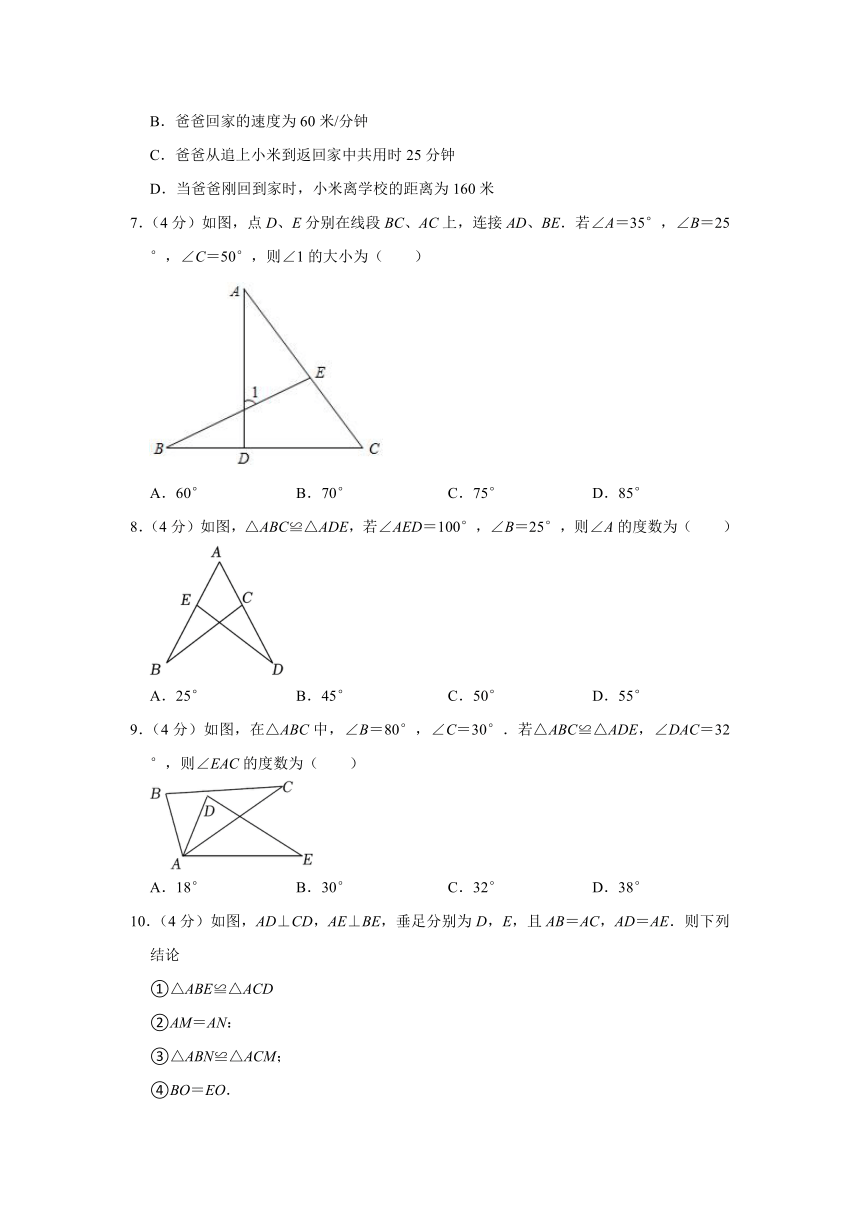
5.(4分)如图,直线y=2x与y=kx+b相交于点P(m,2),则关于x的方程kx+b=2的解是( )
A.x= B.x=1 C.x=2 D.x=4
6.(4分)某天早晨,小米从家出发匀速步行到学校.小米出发一段时间后,爸爸发现小米忘带了数学作业,立即下楼骑自行车,沿小米行进的路线匀速去追小米.爸爸追上小米后将数学作业交给小米后,立即沿原路线匀速返回家里,但由于路上行人渐多,爸爸返回时骑车的速度只有原来速度的一半.小米继续以原速步行前往学校.爸爸与小米之间的距离y(米)与小米从家出发后步行的时间x(分)之间的关系如图所示(小米和爸爸上、下楼以及爸爸交数学作业给小米耽搁的时间忽略不计).对于以下说法,正确的结论是( )
A.学校离家的距离是1000米
B.爸爸回家的速度为60米/分钟
C.爸爸从追上小米到返回家中共用时25分钟
D.当爸爸刚回到家时,小米离学校的距离为160米
7.(4分)如图,点D、E分别在线段BC、AC上,连接AD、BE.若∠A=35°,∠B=25°,∠C=50°,则∠1的大小为( )
A.60° B.70° C.75° D.85°
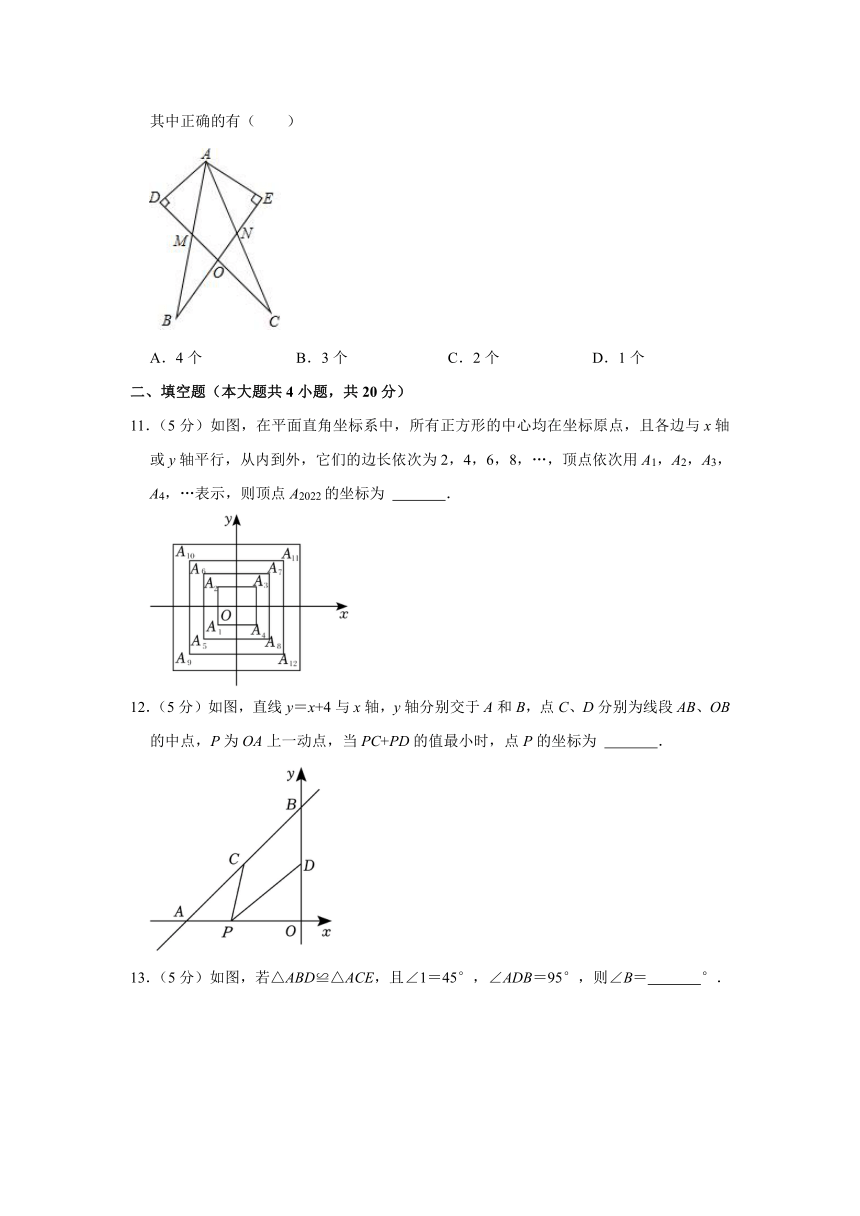
8.(4分)如图,△ABC≌△ADE,若∠AED=100°,∠B=25°,则∠A的度数为( )
A.25° B.45° C.50° D.55°
9.(4分)如图,在△ABC中,∠B=80°,∠C=30°.若△ABC≌△ADE,∠DAC=32°,则∠EAC的度数为( )
A.18° B.30° C.32° D.38°
10.(4分)如图,AD⊥CD,AE⊥BE,垂足分别为D,E,且AB=AC,AD=AE.则下列结论
①△ABE≌△ACD
②AM=AN:
③△ABN≌△ACM;
④BO=EO.
其中正确的有( )
A.4个 B.3个 C.2个 D.1个
二、填空题(本大题共4小题,共20分)
11.(5分)如图,在平面直角坐标系中,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1,A2,A3,A4,…表示,则顶点A2022的坐标为 .
12.(5分)如图,直线y=x+4与x轴,y轴分别交于A和B,点C、D分别为线段AB、OB的中点,P为OA上一动点,当PC+PD的值最小时,点P的坐标为 .
13.(5分)如图,若△ABD≌△ACE,且∠1=45°,∠ADB=95°,则∠B= °.
14.(5分)如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯的水平长度DF相等,那么判定△ABC与△DEF全等的依据是 .
三、解答题(本大题共9小题,共90分。解答应写出文字说明,证明过程或演算步骤)
15.(8分)已知:在平面直角坐标系中,点A(3a+2b,4a+b)在第四象限,且到x轴的距离为2,到y轴的距离为1.
(1)求点B(2a+3b,2a+b)的坐标;
(2)若AC∥y轴,且点C到x轴的距离与点A到x轴的距离相等,请直接写出点C的坐标;
(3)在坐标轴上是否存在一点M,使△ACM的面积=△ABC的面积的一半?若存在,请求出点M的坐标;若不存在,请说明理由.
16.(8分)已知一次函数y=kx+b(k≠0)的图象经过点(3,5)与(﹣4,﹣9).
(1)求这个一次函数的解析式;
(2)判断点是否在这个一次函数的图象上;
(3)直接写出关于x的一元一次方程kx+b=0的解.
17.(8分)如图,B,C,E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.
(1)求证:△ABC≌△CDE;
(2)若∠A=72°,求∠BCD的度数.
18.(8分)已知:如图一次函数y1=﹣x﹣2与y2=x﹣4的图象相交于点A.
(1)求点A的坐标;
(2)若一次函数y1=﹣x﹣2与y2=x﹣4的图象与x轴分别相交于点B、C,求△ABC的面积.
(3)结合图象,直接写出y1≥y2时x的取值范围.
19.(10分)如图,在△ABC中,AB=AC,P是BC边上任意一点,PF⊥AB于点F,PE⊥AC于点E,BD为△ABC的高线,BD=8.求PF+PE的值.
20.(10分)某校计划采购凳子,商场有A、B两种型号的凳子出售,并规定:对于A型凳子,采购数量若超过250张,则超出部分可在原价基础上每张优惠a元;B型凳子的售价为40元/张.学校经测算,若购买300张A型凳子需要花费14250元;若购买500张A型凳子需要花费21250元.
(1)求a的值;
(2)学校要采购A、B两种型号凳子共900张,且购买A型凳子不少于150张且不超过B型凳子数量的2倍,请通过计算帮学校决策如何分配购买数量可以使得总采购费用最少?最少是多少元?
21.(12分)如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,AD=DC=2.5,BC=4.
(1)求∠CBE的度数.
(2)求△CDP与△BEP的周长和.
22.(12分)如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
(2)若B、C在DE的两侧(如图所示),且AD=CE,其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.
23.(14分)在“延时课堂”数学实践活动中,同学们了解到,工人师傅常用角尺作一个已知角的角平分线.作法如下:如图①,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M、N重合,过角尺0刻度的顶点P的射线OP就是∠AOB的角平分线.
(1)联系三角形全等的条件,通过证明△OMP≌△ONP,可知∠AOP=∠BOP,即OP平分∠AOB.则这两个三角形全等的依据是 ;
(2)在活动的过程,同学们发现用两个全等的三角形纸片也可以作一个已知角的角平分线.如图②所示,△CDE≌△STR,将全等三角形的一组对应边DE、TR分别放在∠AOB的两边OA、OB上,同时使这组对应边所对的顶点C、S分别落在OB、OA上,此时CE和SR的交点设为点Q,则射线OQ即为∠AOB的角平分线.你认为他们的作法正确吗?并说明理由.
2022-2023学年安徽省滁州市定远县永康片八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(本大题共10小题,共40分。在每小题列出的选项中,选出符合题目的一项)
1.(4分)如图,在直角坐标系中,边长为2的等边△OA1A2的一条边OA2在x的正半轴上,O为坐标原点;将△OA1A2沿x轴正方形依此向右移动4个单位,依次得△A3A4A5,△A6A7A8…,则顶点A2019的坐标为( )
A.(2690,0) B.(2692,0) C.(2694,0) D.无法确定
【分析】观察图形可知,3个点一个循环,每个循环向右移动4个单位,依此可求顶点A2019的坐标.
【解答】解:2019÷3=673,
673×4=2692,
故顶点A2019的坐标是(2692,0).
故选:B.
2.(4分)已知函数y=(m+1)x是正比例函数,且图象在第二、四象限内,则m的值是( )
A.2 B.﹣2 C.±2 D.﹣
【分析】根据正比例函数的定义,正比例函数的性质,可得答案.
【解答】解:由题意,得
m2﹣3=1,且m+1<0,
解得m=﹣2,
故选:B.
3.(4分)若一次函数y=kx+b的图象经过第一、二、四象限,则一次函数y=bx+k的图象大致是( )
A. B.
C. D.
【分析】根据一次函数y=kx+b图象在坐标平面内的位置关系先确定k,b的取值范围,再根据k,b的取值范围确定一次函数y=bx+k图象在坐标平面内的位置关系,从而求解.
【解答】解:一次函数y=kx+b过一、二、四象限,
则函数值y随x的增大而减小,因而k<0;
图象与y轴的正半轴相交则b>0,
因而一次函数y=bx﹣k的一次项系数b>0,
y随x的增大而增大,经过一三象限,
常数项k<0,则函数与y轴负半轴相交,
因而一定经过一三四象限,
故选:D.
4.(4分)一次函数y=kx+b与正比例函数y=kbx(k,b为常数,且kb≠0)在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
【分析】根据一次函数的图象与系数的关系,由一次函数y=kx+b图象分析可得k、b的符号,进而可得k b的符号,从而判断y=kbx的图象是否正确,进而比较可得答案.
【解答】解:根据一次函数的图象分析可得:
A、由一次函数y=kx+b图象可知k>0,b>0,kb>0;正比例函数y=kbx的图象可知kb<0,矛盾,故此选项错误;
B、由一次函数y=kx+b图象可知k>0,b<0;即kb<0,与正比例函数y=kbx的图象可知kb<0,一致,故此选项正确;
C、正比例函数y=kbx的图象没有经过原点,故此选项错误;
D、由一次函数y=kx+b图象可知k<0,b>0;即kb<0,与正比例函数y=kbx的图象可知kb<0,矛盾,故此选项错误;
故选:B.
5.(4分)如图,直线y=2x与y=kx+b相交于点P(m,2),则关于x的方程kx+b=2的解是( )
A.x= B.x=1 C.x=2 D.x=4
【分析】首先利用函数解析式y=2x求出m的值,然后再根据两函数图象的交点横坐标就是关于x的方程kx+b=2的解可得答案.
【解答】解:∵直线y=2x与y=kx+b相交于点P(m,2),
∴2=2m,
∴m=1,
∴P(1,2),
∴当x=1时,y=kx+b=2,
∴关于x的方程kx+b=2的解是x=1,
故选:B.
6.(4分)某天早晨,小米从家出发匀速步行到学校.小米出发一段时间后,爸爸发现小米忘带了数学作业,立即下楼骑自行车,沿小米行进的路线匀速去追小米.爸爸追上小米后将数学作业交给小米后,立即沿原路线匀速返回家里,但由于路上行人渐多,爸爸返回时骑车的速度只有原来速度的一半.小米继续以原速步行前往学校.爸爸与小米之间的距离y(米)与小米从家出发后步行的时间x(分)之间的关系如图所示(小米和爸爸上、下楼以及爸爸交数学作业给小米耽搁的时间忽略不计).对于以下说法,正确的结论是( )
A.学校离家的距离是1000米
B.爸爸回家的速度为60米/分钟
C.爸爸从追上小米到返回家中共用时25分钟
D.当爸爸刚回到家时,小米离学校的距离为160米
【分析】由图象可知:家到学校总路程为1200米,分别求小米和爸爸的速度,妈妈返回时,根据“爸爸返回时骑车的速度只是原来速度的一半”,得速度为60米/分,可得返回时又用了10分钟,此时小米已经走了25分,还剩5分钟的总程.
【解答】解:由图象得:家到学校总路程为1200米,故A错误,不符合题意;
小米步行速度:1200÷30=40(米/分),
由函数图象得出,爸爸在小米10分后出发,15分时追上小米,
设爸爸去时的速度为v米/分,根据题意得,
(15﹣10)v=15×40,
解得v=120,
∴爸爸去时的速度为120米/分,
则爸爸回家时的速度为:120÷2=60(米/分),故B结论正确,符合题意;
则爸爸回家的时间:15×40÷60=10(分),
∴爸爸从追上小米到返回家中共用时(15﹣10)×2=10(分),
故C错误,不符合题意;
(30﹣15﹣10)×40=200(米).即当爸爸刚回到家时,小米离学校的距离为200米,故D错误,不符合题意;
故选:B.
7.(4分)如图,点D、E分别在线段BC、AC上,连接AD、BE.若∠A=35°,∠B=25°,∠C=50°,则∠1的大小为( )
A.60° B.70° C.75° D.85°
【分析】由三角形的内角和定理,可得∠1=180﹣(∠B+∠ADB),∠ADB=∠A+∠C,所以∠1=180°﹣(∠B+∠A+∠C),由此解答即可.
【解答】解:∵∠1=180﹣(∠B+∠ADB),∠ADB=∠A+∠C,
∴∠1=180°﹣(∠B+∠A+∠C)
=180°﹣(25°+35°+50°)
=180°﹣110°
=70°,
故选:B.
8.(4分)如图,△ABC≌△ADE,若∠AED=100°,∠B=25°,则∠A的度数为( )
A.25° B.45° C.50° D.55°
【分析】根据全等三角形对应角相等可得∠AED=∠ACB,再根据三角形的内角和定理列式求出∠A.
【解答】解:∵△ABC≌△ADE,∠AED=100°,
∴∠AED=∠ACB=100°,
∵∠B=25°,
∴∠A=180°﹣100°﹣25°=55°,
故选:D.
9.(4分)如图,在△ABC中,∠B=80°,∠C=30°.若△ABC≌△ADE,∠DAC=32°,则∠EAC的度数为( )
A.18° B.30° C.32° D.38°
【分析】根据三角形的内角定理可得∠BAC的度数,进一步可得∠BAD的度数,根据全等三角形的性质可得∠EAC=∠BAD,即可确定∠EAC的度数.
【解答】解:∵∠B=80°,∠C=30°,
∴∠BAC=70°,
∵∠DAC=32°,
∴∠BAD=38°,
∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠EAC=∠BAD=38°,
故选:D.
10.(4分)如图,AD⊥CD,AE⊥BE,垂足分别为D,E,且AB=AC,AD=AE.则下列结论
①△ABE≌△ACD
②AM=AN:
③△ABN≌△ACM;
④BO=EO.
其中正确的有( )
A.4个 B.3个 C.2个 D.1个
【分析】根据全等三角形的判定和性质进行判断即可.
【解答】解:∵AD⊥CD,AE⊥BE,
∴∠D=∠E=90°,
由得出Rt△ADC≌Rt△AEB,故①正确;
∴∠B=∠C,
由得出△ABN≌△ACM,故③正确,
∴AN=AM,故②正确;
但不能得出BO=EO,
故选:B.
二、填空题(本大题共4小题,共20分)
11.(5分)如图,在平面直角坐标系中,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1,A2,A3,A4,…表示,则顶点A2022的坐标为 (﹣506,506) .
【分析】根据正方形的性质找出部分An点的坐标,根据坐标的变化找出变化规律“A4n+1(﹣n﹣1,﹣n﹣1),A4n+2(﹣n﹣1,n+1),A4n+3(n+1,n+1),A4n+4(n+1,﹣n﹣1)(n为自然数)”,依此即可得出结论.
【解答】解:观察发现:A1(﹣1,﹣1),A2(﹣1,1),A3(1,1),A4(1,﹣1),A5(﹣2,﹣2),A6(﹣2,2),A7(2,2),A8(2,﹣2),A9(﹣3,﹣3),…,
∴A4n+1(﹣n﹣1,﹣n﹣1),A4n+2(﹣n﹣1,n+1),A4n+3(n+1,n+1),A4n+4(n+1,﹣n﹣1)(n为自然数),
∵2022=505×4+2,
∴A2022(﹣506,506).
故答案为:(﹣506,506).
12.(5分)如图,直线y=x+4与x轴,y轴分别交于A和B,点C、D分别为线段AB、OB的中点,P为OA上一动点,当PC+PD的值最小时,点P的坐标为 (﹣1,0) .
【分析】根据一次函数解析式求出点A、B的坐标,再由中点坐标公式求出点C、D的坐标,根据对称的性质找出点D′的坐标,结合点C、D′的坐标求出直线CD′的解析式,令y=0即可求出x的值,从而得出点P的坐标.
【解答】解:作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,最小值为CD′,如图.
令y=x+4中x=0,则y=4,
∴点B的坐标为(0,4);
令y=x+4中y=0,则x+4=0,解得:x=﹣4,
∴点A的坐标为(﹣4,0).
∵点C、D分别为线段AB、OB的中点,
∴点C(﹣2,2),点D(0,2).
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,﹣2).
设直线CD′的解析式为y=kx+b,
∵直线CD′过点C(﹣2,2),D′(0,﹣2),
∴,解得,
∴直线CD′的解析式为y=﹣2x﹣2.
令y=0,则0=﹣2x﹣2,解得:x=﹣1,
∴点P的坐标为(﹣1,0).
故答案为:(﹣1,0).
13.(5分)如图,若△ABD≌△ACE,且∠1=45°,∠ADB=95°,则∠B= 50 °.
【分析】根据全等三角形的性质及三角形外角性质求解即可.
【解答】解:∵△ABD≌△ACE,∠ADB=95°,
∴∠AEC=∠ADB=95°,
∵∠AEC=∠1+∠B,∠1=45°,
∴∠B=50°,
故答案为:50.
14.(5分)如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯的水平长度DF相等,那么判定△ABC与△DEF全等的依据是 HL .
【分析】根据BC=EF,AC=DF判断可出Rt△ABC≌Rt△DEF.
【解答】解:∵滑梯、墙、地面正好构成直角三角形,
在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL),
故答案为:HL.
三、解答题(本大题共9小题,共90分。解答应写出文字说明,证明过程或演算步骤)
15.(8分)已知:在平面直角坐标系中,点A(3a+2b,4a+b)在第四象限,且到x轴的距离为2,到y轴的距离为1.
(1)求点B(2a+3b,2a+b)的坐标;
(2)若AC∥y轴,且点C到x轴的距离与点A到x轴的距离相等,请直接写出点C的坐标;
(3)在坐标轴上是否存在一点M,使△ACM的面积=△ABC的面积的一半?若存在,请求出点M的坐标;若不存在,请说明理由.
【分析】(1)根据题意求出点A的坐标,列出方程组,解方程组求出a、b,进而求出点B的坐标;
(2)根据轴对称的性质求出点C的坐标;
(3)分点M在y轴上、点M在x轴上两种情况,根据三角形的面积公式计算即可.
【解答】解:(1)∵点A在第四象限,且到x轴的距离为2,到y轴的距离为1,
∴点A的坐标为(1,﹣2),
则,
解得:,
∴2a+3b=﹣4,2a+b=0,
∴点B的坐标为(4,0);
(2)∵AC∥y轴,且点C到x轴的距离与点A到x轴的距离相等,
∴点A与点C关于x轴对称,
∴点C的坐标为(1,2);
(3)存在,
理由如下:∵点A的坐标为(1,﹣2),点C的坐标为(1,2),
∴AC=4,
∴S△ABC=×4×3=6,
当点M在y轴上时,S△ACM=×4×1=2,
∴y轴上不存在一点M,使△ACM的面积=△ABC的面积的一半,
当点M在x轴上时,设点M的坐标为(m,0),
则×4×|m﹣1|=×6,
解得:m=﹣或,
∴点M的坐标为(﹣,0)或(,0)时,△ACM的面积=△ABC的面积的一半.
16.(8分)已知一次函数y=kx+b(k≠0)的图象经过点(3,5)与(﹣4,﹣9).
(1)求这个一次函数的解析式;
(2)判断点是否在这个一次函数的图象上;
(3)直接写出关于x的一元一次方程kx+b=0的解.
【分析】(1)待定系数法求解析式即可;
(2)将代入一次函数解析式求出y的值,即可判断;
(3)由(2)可知一次函数过点(,0),即可求出方程kx+b=0的解.
【解答】解:(1)∵一次函数y=kx+b(k≠0)的图象经过点(3,5)与(﹣4,﹣9),
可得,
解得,
∴这个一次函数的解析式为y=2x﹣1;
(2)当时,,
∴点C(,0)在这个一次函数的图象上;
(3)由(2)可得一元一次方程kx+b=0的解.
17.(8分)如图,B,C,E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.
(1)求证:△ABC≌△CDE;
(2)若∠A=72°,求∠BCD的度数.
【分析】(1)根据AC∥DE,证得∠ACD=∠D,∠BCA=∠E,通过等量代换可知∠B=∠D,再根据AC=CE,可证△ABC≌△CDE;
(2)利用△ABC≌△CDE,得出∠A=∠DCE=72°,再利用平角的定义得出结论即可.
【解答】(1)证明:∵AC∥DE,
∴∠ACD=∠D,∠BCA=∠E,
又∵∠ACD=∠B,
∴∠B=∠D,
在△ABC和△CDE中,
,
∴△ABC≌△CDE(AAS);
(2)解:∵△ABC≌△CDE,
∴∠A=∠DCE=72°,
∴∠BCD=180°﹣72°=108°.
18.(8分)已知:如图一次函数y1=﹣x﹣2与y2=x﹣4的图象相交于点A.
(1)求点A的坐标;
(2)若一次函数y1=﹣x﹣2与y2=x﹣4的图象与x轴分别相交于点B、C,求△ABC的面积.
(3)结合图象,直接写出y1≥y2时x的取值范围.
【分析】(1)将两个函数的解析式联立得到方程组,解此方程组即可求出点A的坐标;
(2)先根据函数解析式求得B、C两点的坐标,可得BC的长,再利用三角形的面积公式可得结果;
(3)根据函数图象以及点A坐标即可求解.
【解答】解:(1)解方程组,得,
所以点A坐标为(1,﹣3);
(2)当y1=0时,﹣x﹣2=0,x=﹣2,则B点坐标为(﹣2,0);
当y2=0时,x﹣4=0,x=4,则C点坐标为(4,0);
∴BC=4﹣(﹣2)=6,
∴△ABC的面积=×6×3=9;
(3)根据图象可知,y1≥y2时x的取值范围是x≤1.
19.(10分)如图,在△ABC中,AB=AC,P是BC边上任意一点,PF⊥AB于点F,PE⊥AC于点E,BD为△ABC的高线,BD=8.求PF+PE的值.
【分析】连接AP,根据S△ABC=S△ABP+S△ACP列式整理即可得解.
【解答】解:连结AP,
∵BD为△ABC的高线,
∴S△ABC=BD AC.
∵PE⊥AB,PF⊥AC,AB=AC,
∴S△ABC=S△ABP+S△ACP=AB PF+AC PE=AC (PE+PF),
∴BD=PF+PE.
∴PF+PE=8.
20.(10分)某校计划采购凳子,商场有A、B两种型号的凳子出售,并规定:对于A型凳子,采购数量若超过250张,则超出部分可在原价基础上每张优惠a元;B型凳子的售价为40元/张.学校经测算,若购买300张A型凳子需要花费14250元;若购买500张A型凳子需要花费21250元.
(1)求a的值;
(2)学校要采购A、B两种型号凳子共900张,且购买A型凳子不少于150张且不超过B型凳子数量的2倍,请通过计算帮学校决策如何分配购买数量可以使得总采购费用最少?最少是多少元?
【分析】(1)设A型凳子的售价为x张,根据题意列方程组解答即可;
(2)设购买A型凳子m张,则购买B型凳子(900﹣m)张,根据题意求出m的取值范围;设总采购费用为w元,根据题意得出w与m的函数关系式,再根据一次函数的性质解答即可.
【解答】解:(1)设A型凳子的售价为x元/张,根据题意得
,
解得,
答:a的值为15.
(2)设购买A型凳子m张,则购买B型凳子(900﹣m)张,
根据题意得,
解得150≤m≤600,
设总采购费用为w元,根据题意得
当150≤m≤250时,w=50m+40(900﹣m)=10m+36000;
当250<m≤600时,w=50×250+(50﹣15)×(m﹣250)+40(900﹣m)=﹣5m+39750,
∴,
当150≤m≤250时,10>0,w随m的增大而增大,m=150时,w的最小值为37500;
当250<m≤600时,﹣5<0,w随m的增大而减小,m=600时,w的最小值为36750.
∵37500>36750,
∴购买A型凳子600张,购买B型凳子300张时总采购费用最少,最少是36750元.
21.(12分)如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,AD=DC=2.5,BC=4.
(1)求∠CBE的度数.
(2)求△CDP与△BEP的周长和.
【分析】(1)根据全等三角形的性质得到∠ABC=∠DBE,计算即可;
(2)根据全等三角形的性质求出BE、DE,根据三角形的周长公式计算即可.
【解答】解:(1)∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE,
∴∠ABD=∠CBE=132°÷2=66°,
即∠CBE的度数为66°;
(2)∵△ABC≌△DBE,
∴DE=AC=AD+DC=5,BE=BC=4,
∴△CDP与△BEP的周长和=DC+DP+PC+BP+PE+BE=DC+DE+BC+BE=2.5+5+4+4=15.5.
22.(12分)如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
(2)若B、C在DE的两侧(如图所示),且AD=CE,其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.
【分析】(1)由已知条件,证明Rt△ABD≌Rt△CAE,再利用角与角之间的关系求证∠BAD+∠CAE=90°,即可证明AB⊥AC;
(2)同(1),先证Rt△ABD≌Rt△CAE,再利用角与角之间的关系求证∠BAD+∠CAE=90°,即可证明AB⊥AC.
【解答】(1)证明:∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°,
在Rt△ABD和Rt△ACE中,
∵,
∴Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠EAC.
∵∠DAB+∠DBA=90°,∠EAC+∠ACE=90°,
∴∠BAD+∠CAE=90°.
∠BAC=180°﹣(∠BAD+∠CAE)=90°.
∴AB⊥AC.
(2)AB⊥AC.理由如下:
同(1)一样可证得Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠EAC,
∵∠CAE+∠ECA=90°,
∴∠CAE+∠BAD=90°,即∠BAC=90°,
∴AB⊥AC.
23.(14分)在“延时课堂”数学实践活动中,同学们了解到,工人师傅常用角尺作一个已知角的角平分线.作法如下:如图①,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M、N重合,过角尺0刻度的顶点P的射线OP就是∠AOB的角平分线.
(1)联系三角形全等的条件,通过证明△OMP≌△ONP,可知∠AOP=∠BOP,即OP平分∠AOB.则这两个三角形全等的依据是 SSS ;
(2)在活动的过程,同学们发现用两个全等的三角形纸片也可以作一个已知角的角平分线.如图②所示,△CDE≌△STR,将全等三角形的一组对应边DE、TR分别放在∠AOB的两边OA、OB上,同时使这组对应边所对的顶点C、S分别落在OB、OA上,此时CE和SR的交点设为点Q,则射线OQ即为∠AOB的角平分线.你认为他们的作法正确吗?并说明理由.
【分析】(1)利用SSS证明三角形全等即可;
(2)证明△ECO≌△RSO(AAS),推出OE=PR,同法可证,△STO≌△CDO(AAS),推出OS=OC,SE=CR,再证明△SQE≌△CQR(AAS),推出SQ=CQ,证明△OQS≌△OQC(SSS),可得∠QOA=∠QOB.
【解答】解:(1)在△POM和△PON中,
,
∴△POM≌△PON(SSS),
∴∠POA=∠POB,
故答案为:SSS;
(2)正确.
理由:如图2中,∵△CDE≌△STR,
∴EC=RS,∠CED=∠SRT,
在△ECO和△RSO中,
,
∴△ECO≌△RSO(AAS),
∴OE=OR,
同法可证,△STO≌△CDO(AAS),
∴OS=OC,
∴SE=CR,
在△SQE和△CQR中,
,
∴△SQE≌△CQR(AAS),
∴SQ=CQ,
在△OQS和△OQC中,
,
∴△OQS≌△OQC(SSS),
∴∠QOA=∠QOB.
一、选择题(本大题共10小题,共40分。在每小题列出的选项中,选出符合题目的一项)
1.(4分)如图,在直角坐标系中,边长为2的等边△OA1A2的一条边OA2在x的正半轴上,O为坐标原点;将△OA1A2沿x轴正方形依此向右移动4个单位,依次得△A3A4A5,△A6A7A8…,则顶点A2019的坐标为( )
A.(2690,0) B.(2692,0) C.(2694,0) D.无法确定
2.(4分)已知函数y=(m+1)x是正比例函数,且图象在第二、四象限内,则m的值是( )
A.2 B.﹣2 C.±2 D.﹣
3.(4分)若一次函数y=kx+b的图象经过第一、二、四象限,则一次函数y=bx+k的图象大致是( )
A. B.
C. D.
4.(4分)一次函数y=kx+b与正比例函数y=kbx(k,b为常数,且kb≠0)在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
5.(4分)如图,直线y=2x与y=kx+b相交于点P(m,2),则关于x的方程kx+b=2的解是( )
A.x= B.x=1 C.x=2 D.x=4
6.(4分)某天早晨,小米从家出发匀速步行到学校.小米出发一段时间后,爸爸发现小米忘带了数学作业,立即下楼骑自行车,沿小米行进的路线匀速去追小米.爸爸追上小米后将数学作业交给小米后,立即沿原路线匀速返回家里,但由于路上行人渐多,爸爸返回时骑车的速度只有原来速度的一半.小米继续以原速步行前往学校.爸爸与小米之间的距离y(米)与小米从家出发后步行的时间x(分)之间的关系如图所示(小米和爸爸上、下楼以及爸爸交数学作业给小米耽搁的时间忽略不计).对于以下说法,正确的结论是( )
A.学校离家的距离是1000米
B.爸爸回家的速度为60米/分钟
C.爸爸从追上小米到返回家中共用时25分钟
D.当爸爸刚回到家时,小米离学校的距离为160米
7.(4分)如图,点D、E分别在线段BC、AC上,连接AD、BE.若∠A=35°,∠B=25°,∠C=50°,则∠1的大小为( )
A.60° B.70° C.75° D.85°
8.(4分)如图,△ABC≌△ADE,若∠AED=100°,∠B=25°,则∠A的度数为( )
A.25° B.45° C.50° D.55°
9.(4分)如图,在△ABC中,∠B=80°,∠C=30°.若△ABC≌△ADE,∠DAC=32°,则∠EAC的度数为( )
A.18° B.30° C.32° D.38°
10.(4分)如图,AD⊥CD,AE⊥BE,垂足分别为D,E,且AB=AC,AD=AE.则下列结论
①△ABE≌△ACD
②AM=AN:
③△ABN≌△ACM;
④BO=EO.
其中正确的有( )
A.4个 B.3个 C.2个 D.1个
二、填空题(本大题共4小题,共20分)
11.(5分)如图,在平面直角坐标系中,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1,A2,A3,A4,…表示,则顶点A2022的坐标为 .
12.(5分)如图,直线y=x+4与x轴,y轴分别交于A和B,点C、D分别为线段AB、OB的中点,P为OA上一动点,当PC+PD的值最小时,点P的坐标为 .
13.(5分)如图,若△ABD≌△ACE,且∠1=45°,∠ADB=95°,则∠B= °.
14.(5分)如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯的水平长度DF相等,那么判定△ABC与△DEF全等的依据是 .
三、解答题(本大题共9小题,共90分。解答应写出文字说明,证明过程或演算步骤)
15.(8分)已知:在平面直角坐标系中,点A(3a+2b,4a+b)在第四象限,且到x轴的距离为2,到y轴的距离为1.
(1)求点B(2a+3b,2a+b)的坐标;
(2)若AC∥y轴,且点C到x轴的距离与点A到x轴的距离相等,请直接写出点C的坐标;
(3)在坐标轴上是否存在一点M,使△ACM的面积=△ABC的面积的一半?若存在,请求出点M的坐标;若不存在,请说明理由.
16.(8分)已知一次函数y=kx+b(k≠0)的图象经过点(3,5)与(﹣4,﹣9).
(1)求这个一次函数的解析式;
(2)判断点是否在这个一次函数的图象上;
(3)直接写出关于x的一元一次方程kx+b=0的解.
17.(8分)如图,B,C,E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.
(1)求证:△ABC≌△CDE;
(2)若∠A=72°,求∠BCD的度数.
18.(8分)已知:如图一次函数y1=﹣x﹣2与y2=x﹣4的图象相交于点A.
(1)求点A的坐标;
(2)若一次函数y1=﹣x﹣2与y2=x﹣4的图象与x轴分别相交于点B、C,求△ABC的面积.
(3)结合图象,直接写出y1≥y2时x的取值范围.
19.(10分)如图,在△ABC中,AB=AC,P是BC边上任意一点,PF⊥AB于点F,PE⊥AC于点E,BD为△ABC的高线,BD=8.求PF+PE的值.
20.(10分)某校计划采购凳子,商场有A、B两种型号的凳子出售,并规定:对于A型凳子,采购数量若超过250张,则超出部分可在原价基础上每张优惠a元;B型凳子的售价为40元/张.学校经测算,若购买300张A型凳子需要花费14250元;若购买500张A型凳子需要花费21250元.
(1)求a的值;
(2)学校要采购A、B两种型号凳子共900张,且购买A型凳子不少于150张且不超过B型凳子数量的2倍,请通过计算帮学校决策如何分配购买数量可以使得总采购费用最少?最少是多少元?
21.(12分)如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,AD=DC=2.5,BC=4.
(1)求∠CBE的度数.
(2)求△CDP与△BEP的周长和.
22.(12分)如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
(2)若B、C在DE的两侧(如图所示),且AD=CE,其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.
23.(14分)在“延时课堂”数学实践活动中,同学们了解到,工人师傅常用角尺作一个已知角的角平分线.作法如下:如图①,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M、N重合,过角尺0刻度的顶点P的射线OP就是∠AOB的角平分线.
(1)联系三角形全等的条件,通过证明△OMP≌△ONP,可知∠AOP=∠BOP,即OP平分∠AOB.则这两个三角形全等的依据是 ;
(2)在活动的过程,同学们发现用两个全等的三角形纸片也可以作一个已知角的角平分线.如图②所示,△CDE≌△STR,将全等三角形的一组对应边DE、TR分别放在∠AOB的两边OA、OB上,同时使这组对应边所对的顶点C、S分别落在OB、OA上,此时CE和SR的交点设为点Q,则射线OQ即为∠AOB的角平分线.你认为他们的作法正确吗?并说明理由.
2022-2023学年安徽省滁州市定远县永康片八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(本大题共10小题,共40分。在每小题列出的选项中,选出符合题目的一项)
1.(4分)如图,在直角坐标系中,边长为2的等边△OA1A2的一条边OA2在x的正半轴上,O为坐标原点;将△OA1A2沿x轴正方形依此向右移动4个单位,依次得△A3A4A5,△A6A7A8…,则顶点A2019的坐标为( )
A.(2690,0) B.(2692,0) C.(2694,0) D.无法确定
【分析】观察图形可知,3个点一个循环,每个循环向右移动4个单位,依此可求顶点A2019的坐标.
【解答】解:2019÷3=673,
673×4=2692,
故顶点A2019的坐标是(2692,0).
故选:B.
2.(4分)已知函数y=(m+1)x是正比例函数,且图象在第二、四象限内,则m的值是( )
A.2 B.﹣2 C.±2 D.﹣
【分析】根据正比例函数的定义,正比例函数的性质,可得答案.
【解答】解:由题意,得
m2﹣3=1,且m+1<0,
解得m=﹣2,
故选:B.
3.(4分)若一次函数y=kx+b的图象经过第一、二、四象限,则一次函数y=bx+k的图象大致是( )
A. B.
C. D.
【分析】根据一次函数y=kx+b图象在坐标平面内的位置关系先确定k,b的取值范围,再根据k,b的取值范围确定一次函数y=bx+k图象在坐标平面内的位置关系,从而求解.
【解答】解:一次函数y=kx+b过一、二、四象限,
则函数值y随x的增大而减小,因而k<0;
图象与y轴的正半轴相交则b>0,
因而一次函数y=bx﹣k的一次项系数b>0,
y随x的增大而增大,经过一三象限,
常数项k<0,则函数与y轴负半轴相交,
因而一定经过一三四象限,
故选:D.
4.(4分)一次函数y=kx+b与正比例函数y=kbx(k,b为常数,且kb≠0)在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
【分析】根据一次函数的图象与系数的关系,由一次函数y=kx+b图象分析可得k、b的符号,进而可得k b的符号,从而判断y=kbx的图象是否正确,进而比较可得答案.
【解答】解:根据一次函数的图象分析可得:
A、由一次函数y=kx+b图象可知k>0,b>0,kb>0;正比例函数y=kbx的图象可知kb<0,矛盾,故此选项错误;
B、由一次函数y=kx+b图象可知k>0,b<0;即kb<0,与正比例函数y=kbx的图象可知kb<0,一致,故此选项正确;
C、正比例函数y=kbx的图象没有经过原点,故此选项错误;
D、由一次函数y=kx+b图象可知k<0,b>0;即kb<0,与正比例函数y=kbx的图象可知kb<0,矛盾,故此选项错误;
故选:B.
5.(4分)如图,直线y=2x与y=kx+b相交于点P(m,2),则关于x的方程kx+b=2的解是( )
A.x= B.x=1 C.x=2 D.x=4
【分析】首先利用函数解析式y=2x求出m的值,然后再根据两函数图象的交点横坐标就是关于x的方程kx+b=2的解可得答案.
【解答】解:∵直线y=2x与y=kx+b相交于点P(m,2),
∴2=2m,
∴m=1,
∴P(1,2),
∴当x=1时,y=kx+b=2,
∴关于x的方程kx+b=2的解是x=1,
故选:B.
6.(4分)某天早晨,小米从家出发匀速步行到学校.小米出发一段时间后,爸爸发现小米忘带了数学作业,立即下楼骑自行车,沿小米行进的路线匀速去追小米.爸爸追上小米后将数学作业交给小米后,立即沿原路线匀速返回家里,但由于路上行人渐多,爸爸返回时骑车的速度只有原来速度的一半.小米继续以原速步行前往学校.爸爸与小米之间的距离y(米)与小米从家出发后步行的时间x(分)之间的关系如图所示(小米和爸爸上、下楼以及爸爸交数学作业给小米耽搁的时间忽略不计).对于以下说法,正确的结论是( )
A.学校离家的距离是1000米
B.爸爸回家的速度为60米/分钟
C.爸爸从追上小米到返回家中共用时25分钟
D.当爸爸刚回到家时,小米离学校的距离为160米
【分析】由图象可知:家到学校总路程为1200米,分别求小米和爸爸的速度,妈妈返回时,根据“爸爸返回时骑车的速度只是原来速度的一半”,得速度为60米/分,可得返回时又用了10分钟,此时小米已经走了25分,还剩5分钟的总程.
【解答】解:由图象得:家到学校总路程为1200米,故A错误,不符合题意;
小米步行速度:1200÷30=40(米/分),
由函数图象得出,爸爸在小米10分后出发,15分时追上小米,
设爸爸去时的速度为v米/分,根据题意得,
(15﹣10)v=15×40,
解得v=120,
∴爸爸去时的速度为120米/分,
则爸爸回家时的速度为:120÷2=60(米/分),故B结论正确,符合题意;
则爸爸回家的时间:15×40÷60=10(分),
∴爸爸从追上小米到返回家中共用时(15﹣10)×2=10(分),
故C错误,不符合题意;
(30﹣15﹣10)×40=200(米).即当爸爸刚回到家时,小米离学校的距离为200米,故D错误,不符合题意;
故选:B.
7.(4分)如图,点D、E分别在线段BC、AC上,连接AD、BE.若∠A=35°,∠B=25°,∠C=50°,则∠1的大小为( )
A.60° B.70° C.75° D.85°
【分析】由三角形的内角和定理,可得∠1=180﹣(∠B+∠ADB),∠ADB=∠A+∠C,所以∠1=180°﹣(∠B+∠A+∠C),由此解答即可.
【解答】解:∵∠1=180﹣(∠B+∠ADB),∠ADB=∠A+∠C,
∴∠1=180°﹣(∠B+∠A+∠C)
=180°﹣(25°+35°+50°)
=180°﹣110°
=70°,
故选:B.
8.(4分)如图,△ABC≌△ADE,若∠AED=100°,∠B=25°,则∠A的度数为( )
A.25° B.45° C.50° D.55°
【分析】根据全等三角形对应角相等可得∠AED=∠ACB,再根据三角形的内角和定理列式求出∠A.
【解答】解:∵△ABC≌△ADE,∠AED=100°,
∴∠AED=∠ACB=100°,
∵∠B=25°,
∴∠A=180°﹣100°﹣25°=55°,
故选:D.
9.(4分)如图,在△ABC中,∠B=80°,∠C=30°.若△ABC≌△ADE,∠DAC=32°,则∠EAC的度数为( )
A.18° B.30° C.32° D.38°
【分析】根据三角形的内角定理可得∠BAC的度数,进一步可得∠BAD的度数,根据全等三角形的性质可得∠EAC=∠BAD,即可确定∠EAC的度数.
【解答】解:∵∠B=80°,∠C=30°,
∴∠BAC=70°,
∵∠DAC=32°,
∴∠BAD=38°,
∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠EAC=∠BAD=38°,
故选:D.
10.(4分)如图,AD⊥CD,AE⊥BE,垂足分别为D,E,且AB=AC,AD=AE.则下列结论
①△ABE≌△ACD
②AM=AN:
③△ABN≌△ACM;
④BO=EO.
其中正确的有( )
A.4个 B.3个 C.2个 D.1个
【分析】根据全等三角形的判定和性质进行判断即可.
【解答】解:∵AD⊥CD,AE⊥BE,
∴∠D=∠E=90°,
由得出Rt△ADC≌Rt△AEB,故①正确;
∴∠B=∠C,
由得出△ABN≌△ACM,故③正确,
∴AN=AM,故②正确;
但不能得出BO=EO,
故选:B.
二、填空题(本大题共4小题,共20分)
11.(5分)如图,在平面直角坐标系中,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1,A2,A3,A4,…表示,则顶点A2022的坐标为 (﹣506,506) .
【分析】根据正方形的性质找出部分An点的坐标,根据坐标的变化找出变化规律“A4n+1(﹣n﹣1,﹣n﹣1),A4n+2(﹣n﹣1,n+1),A4n+3(n+1,n+1),A4n+4(n+1,﹣n﹣1)(n为自然数)”,依此即可得出结论.
【解答】解:观察发现:A1(﹣1,﹣1),A2(﹣1,1),A3(1,1),A4(1,﹣1),A5(﹣2,﹣2),A6(﹣2,2),A7(2,2),A8(2,﹣2),A9(﹣3,﹣3),…,
∴A4n+1(﹣n﹣1,﹣n﹣1),A4n+2(﹣n﹣1,n+1),A4n+3(n+1,n+1),A4n+4(n+1,﹣n﹣1)(n为自然数),
∵2022=505×4+2,
∴A2022(﹣506,506).
故答案为:(﹣506,506).
12.(5分)如图,直线y=x+4与x轴,y轴分别交于A和B,点C、D分别为线段AB、OB的中点,P为OA上一动点,当PC+PD的值最小时,点P的坐标为 (﹣1,0) .
【分析】根据一次函数解析式求出点A、B的坐标,再由中点坐标公式求出点C、D的坐标,根据对称的性质找出点D′的坐标,结合点C、D′的坐标求出直线CD′的解析式,令y=0即可求出x的值,从而得出点P的坐标.
【解答】解:作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,最小值为CD′,如图.
令y=x+4中x=0,则y=4,
∴点B的坐标为(0,4);
令y=x+4中y=0,则x+4=0,解得:x=﹣4,
∴点A的坐标为(﹣4,0).
∵点C、D分别为线段AB、OB的中点,
∴点C(﹣2,2),点D(0,2).
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,﹣2).
设直线CD′的解析式为y=kx+b,
∵直线CD′过点C(﹣2,2),D′(0,﹣2),
∴,解得,
∴直线CD′的解析式为y=﹣2x﹣2.
令y=0,则0=﹣2x﹣2,解得:x=﹣1,
∴点P的坐标为(﹣1,0).
故答案为:(﹣1,0).
13.(5分)如图,若△ABD≌△ACE,且∠1=45°,∠ADB=95°,则∠B= 50 °.
【分析】根据全等三角形的性质及三角形外角性质求解即可.
【解答】解:∵△ABD≌△ACE,∠ADB=95°,
∴∠AEC=∠ADB=95°,
∵∠AEC=∠1+∠B,∠1=45°,
∴∠B=50°,
故答案为:50.
14.(5分)如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯的水平长度DF相等,那么判定△ABC与△DEF全等的依据是 HL .
【分析】根据BC=EF,AC=DF判断可出Rt△ABC≌Rt△DEF.
【解答】解:∵滑梯、墙、地面正好构成直角三角形,
在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL),
故答案为:HL.
三、解答题(本大题共9小题,共90分。解答应写出文字说明,证明过程或演算步骤)
15.(8分)已知:在平面直角坐标系中,点A(3a+2b,4a+b)在第四象限,且到x轴的距离为2,到y轴的距离为1.
(1)求点B(2a+3b,2a+b)的坐标;
(2)若AC∥y轴,且点C到x轴的距离与点A到x轴的距离相等,请直接写出点C的坐标;
(3)在坐标轴上是否存在一点M,使△ACM的面积=△ABC的面积的一半?若存在,请求出点M的坐标;若不存在,请说明理由.
【分析】(1)根据题意求出点A的坐标,列出方程组,解方程组求出a、b,进而求出点B的坐标;
(2)根据轴对称的性质求出点C的坐标;
(3)分点M在y轴上、点M在x轴上两种情况,根据三角形的面积公式计算即可.
【解答】解:(1)∵点A在第四象限,且到x轴的距离为2,到y轴的距离为1,
∴点A的坐标为(1,﹣2),
则,
解得:,
∴2a+3b=﹣4,2a+b=0,
∴点B的坐标为(4,0);
(2)∵AC∥y轴,且点C到x轴的距离与点A到x轴的距离相等,
∴点A与点C关于x轴对称,
∴点C的坐标为(1,2);
(3)存在,
理由如下:∵点A的坐标为(1,﹣2),点C的坐标为(1,2),
∴AC=4,
∴S△ABC=×4×3=6,
当点M在y轴上时,S△ACM=×4×1=2,
∴y轴上不存在一点M,使△ACM的面积=△ABC的面积的一半,
当点M在x轴上时,设点M的坐标为(m,0),
则×4×|m﹣1|=×6,
解得:m=﹣或,
∴点M的坐标为(﹣,0)或(,0)时,△ACM的面积=△ABC的面积的一半.
16.(8分)已知一次函数y=kx+b(k≠0)的图象经过点(3,5)与(﹣4,﹣9).
(1)求这个一次函数的解析式;
(2)判断点是否在这个一次函数的图象上;
(3)直接写出关于x的一元一次方程kx+b=0的解.
【分析】(1)待定系数法求解析式即可;
(2)将代入一次函数解析式求出y的值,即可判断;
(3)由(2)可知一次函数过点(,0),即可求出方程kx+b=0的解.
【解答】解:(1)∵一次函数y=kx+b(k≠0)的图象经过点(3,5)与(﹣4,﹣9),
可得,
解得,
∴这个一次函数的解析式为y=2x﹣1;
(2)当时,,
∴点C(,0)在这个一次函数的图象上;
(3)由(2)可得一元一次方程kx+b=0的解.
17.(8分)如图,B,C,E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.
(1)求证:△ABC≌△CDE;
(2)若∠A=72°,求∠BCD的度数.
【分析】(1)根据AC∥DE,证得∠ACD=∠D,∠BCA=∠E,通过等量代换可知∠B=∠D,再根据AC=CE,可证△ABC≌△CDE;
(2)利用△ABC≌△CDE,得出∠A=∠DCE=72°,再利用平角的定义得出结论即可.
【解答】(1)证明:∵AC∥DE,
∴∠ACD=∠D,∠BCA=∠E,
又∵∠ACD=∠B,
∴∠B=∠D,
在△ABC和△CDE中,
,
∴△ABC≌△CDE(AAS);
(2)解:∵△ABC≌△CDE,
∴∠A=∠DCE=72°,
∴∠BCD=180°﹣72°=108°.
18.(8分)已知:如图一次函数y1=﹣x﹣2与y2=x﹣4的图象相交于点A.
(1)求点A的坐标;
(2)若一次函数y1=﹣x﹣2与y2=x﹣4的图象与x轴分别相交于点B、C,求△ABC的面积.
(3)结合图象,直接写出y1≥y2时x的取值范围.
【分析】(1)将两个函数的解析式联立得到方程组,解此方程组即可求出点A的坐标;
(2)先根据函数解析式求得B、C两点的坐标,可得BC的长,再利用三角形的面积公式可得结果;
(3)根据函数图象以及点A坐标即可求解.
【解答】解:(1)解方程组,得,
所以点A坐标为(1,﹣3);
(2)当y1=0时,﹣x﹣2=0,x=﹣2,则B点坐标为(﹣2,0);
当y2=0时,x﹣4=0,x=4,则C点坐标为(4,0);
∴BC=4﹣(﹣2)=6,
∴△ABC的面积=×6×3=9;
(3)根据图象可知,y1≥y2时x的取值范围是x≤1.
19.(10分)如图,在△ABC中,AB=AC,P是BC边上任意一点,PF⊥AB于点F,PE⊥AC于点E,BD为△ABC的高线,BD=8.求PF+PE的值.
【分析】连接AP,根据S△ABC=S△ABP+S△ACP列式整理即可得解.
【解答】解:连结AP,
∵BD为△ABC的高线,
∴S△ABC=BD AC.
∵PE⊥AB,PF⊥AC,AB=AC,
∴S△ABC=S△ABP+S△ACP=AB PF+AC PE=AC (PE+PF),
∴BD=PF+PE.
∴PF+PE=8.
20.(10分)某校计划采购凳子,商场有A、B两种型号的凳子出售,并规定:对于A型凳子,采购数量若超过250张,则超出部分可在原价基础上每张优惠a元;B型凳子的售价为40元/张.学校经测算,若购买300张A型凳子需要花费14250元;若购买500张A型凳子需要花费21250元.
(1)求a的值;
(2)学校要采购A、B两种型号凳子共900张,且购买A型凳子不少于150张且不超过B型凳子数量的2倍,请通过计算帮学校决策如何分配购买数量可以使得总采购费用最少?最少是多少元?
【分析】(1)设A型凳子的售价为x张,根据题意列方程组解答即可;
(2)设购买A型凳子m张,则购买B型凳子(900﹣m)张,根据题意求出m的取值范围;设总采购费用为w元,根据题意得出w与m的函数关系式,再根据一次函数的性质解答即可.
【解答】解:(1)设A型凳子的售价为x元/张,根据题意得
,
解得,
答:a的值为15.
(2)设购买A型凳子m张,则购买B型凳子(900﹣m)张,
根据题意得,
解得150≤m≤600,
设总采购费用为w元,根据题意得
当150≤m≤250时,w=50m+40(900﹣m)=10m+36000;
当250<m≤600时,w=50×250+(50﹣15)×(m﹣250)+40(900﹣m)=﹣5m+39750,
∴,
当150≤m≤250时,10>0,w随m的增大而增大,m=150时,w的最小值为37500;
当250<m≤600时,﹣5<0,w随m的增大而减小,m=600时,w的最小值为36750.
∵37500>36750,
∴购买A型凳子600张,购买B型凳子300张时总采购费用最少,最少是36750元.
21.(12分)如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,AD=DC=2.5,BC=4.
(1)求∠CBE的度数.
(2)求△CDP与△BEP的周长和.
【分析】(1)根据全等三角形的性质得到∠ABC=∠DBE,计算即可;
(2)根据全等三角形的性质求出BE、DE,根据三角形的周长公式计算即可.
【解答】解:(1)∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE,
∴∠ABD=∠CBE=132°÷2=66°,
即∠CBE的度数为66°;
(2)∵△ABC≌△DBE,
∴DE=AC=AD+DC=5,BE=BC=4,
∴△CDP与△BEP的周长和=DC+DP+PC+BP+PE+BE=DC+DE+BC+BE=2.5+5+4+4=15.5.
22.(12分)如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
(2)若B、C在DE的两侧(如图所示),且AD=CE,其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.
【分析】(1)由已知条件,证明Rt△ABD≌Rt△CAE,再利用角与角之间的关系求证∠BAD+∠CAE=90°,即可证明AB⊥AC;
(2)同(1),先证Rt△ABD≌Rt△CAE,再利用角与角之间的关系求证∠BAD+∠CAE=90°,即可证明AB⊥AC.
【解答】(1)证明:∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°,
在Rt△ABD和Rt△ACE中,
∵,
∴Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠EAC.
∵∠DAB+∠DBA=90°,∠EAC+∠ACE=90°,
∴∠BAD+∠CAE=90°.
∠BAC=180°﹣(∠BAD+∠CAE)=90°.
∴AB⊥AC.
(2)AB⊥AC.理由如下:
同(1)一样可证得Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠EAC,
∵∠CAE+∠ECA=90°,
∴∠CAE+∠BAD=90°,即∠BAC=90°,
∴AB⊥AC.
23.(14分)在“延时课堂”数学实践活动中,同学们了解到,工人师傅常用角尺作一个已知角的角平分线.作法如下:如图①,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M、N重合,过角尺0刻度的顶点P的射线OP就是∠AOB的角平分线.
(1)联系三角形全等的条件,通过证明△OMP≌△ONP,可知∠AOP=∠BOP,即OP平分∠AOB.则这两个三角形全等的依据是 SSS ;
(2)在活动的过程,同学们发现用两个全等的三角形纸片也可以作一个已知角的角平分线.如图②所示,△CDE≌△STR,将全等三角形的一组对应边DE、TR分别放在∠AOB的两边OA、OB上,同时使这组对应边所对的顶点C、S分别落在OB、OA上,此时CE和SR的交点设为点Q,则射线OQ即为∠AOB的角平分线.你认为他们的作法正确吗?并说明理由.
【分析】(1)利用SSS证明三角形全等即可;
(2)证明△ECO≌△RSO(AAS),推出OE=PR,同法可证,△STO≌△CDO(AAS),推出OS=OC,SE=CR,再证明△SQE≌△CQR(AAS),推出SQ=CQ,证明△OQS≌△OQC(SSS),可得∠QOA=∠QOB.
【解答】解:(1)在△POM和△PON中,
,
∴△POM≌△PON(SSS),
∴∠POA=∠POB,
故答案为:SSS;
(2)正确.
理由:如图2中,∵△CDE≌△STR,
∴EC=RS,∠CED=∠SRT,
在△ECO和△RSO中,
,
∴△ECO≌△RSO(AAS),
∴OE=OR,
同法可证,△STO≌△CDO(AAS),
∴OS=OC,
∴SE=CR,
在△SQE和△CQR中,
,
∴△SQE≌△CQR(AAS),
∴SQ=CQ,
在△OQS和△OQC中,
,
∴△OQS≌△OQC(SSS),
∴∠QOA=∠QOB.
同课章节目录
