2022——2023高一数学期末考试章章通关练——第五章 函数应用1(含解析)
文档属性
| 名称 | 2022——2023高一数学期末考试章章通关练——第五章 函数应用1(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 629.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-19 09:36:58 | ||
图片预览




文档简介
一、单选题
1.在新冠肺炎疫情防控期间,某超市开通网上销售业务,每天能完成1200份订单的配货,由于订单量大幅增加,导致订单积压.为解决困难,许多志愿者踊跃报名参加配货工作.已知该超市某日积压500份订单未配货,预计第二天的新订单超过1600份的概率为0.05,志愿者每人每天能完成50份订单的配货,为使第二天完成积压订单及当日订单的配货的概率不小于0.95,则至少需要志愿者( )
A.10名 B.18名 C.24名 D.32名
2.设为实数,已知函数的两个零点在区间内,则的取值范围是( )
A. B.
C. D.
3.2020年6月17日15时19分,星期三,酒泉卫星发射中心,我国成功发射长征二号丁运载火箭,并成功将高分九号03星、皮星三号A星和德五号卫星送入预定轨道,携三星入轨,全程发射获得圆满成功,祖国威武.已知火箭的最大速度v(单位:)和燃料质量M(单位:),火箭质量m(单位:)的函数关系是:,若已知火箭的质量为3100公斤,燃料质量为310吨,则此时v的值为多少(参考数值为;)( )
A.13.8 B.9240 C.9.24 D.1380
4.当强度为x的声音对应的等级为分贝时,有(其中为常数).装修电钻的声音约为分贝,普通室内谈话的声音约为分贝.则装修电钻的声音强度与普通室内谈话的声音强度的比值为( )
A. B. C. D.
5.通过研究学生的学习行为,心理学家发现,学生的接受能力依赖于老师引入概念和描述所用的时间.若用表示学生掌握和接受概念的能力(越大,表示学生的接受能力越强),表示提出和讲授概念的时间(单位:),长期的实验和分析表明,与有以下关系:则下列说法错误的是( )
A.讲授开始时,学生的兴趣递增;中间有段时间,学生的兴趣保持较理想的状态;随后学生的注意力开始分散
B.讲课开始后第5分钟比讲课开始第20分钟,学生的接受能力更强一点
C.讲课开始后第10分钟到第16分钟,学生的接受能力最强
D.需要13分钟讲解的复杂问题,老师可以在学生的注意力至少达到55以上的情况下完成
6.如图,某池塘里浮萍的面积(单位:)与时间t(单位:月)的关系为,关于下列说法不正确的是( )
A.浮萍每月的增长率为2
B.浮萍每月增加的面积都相等
C.第4个月时,浮萍面积超过
D.若浮萍蔓延到所经过的时间分别是,、,则
7.给出下列函数,其中在上是增函数且不存在零点的函数的是( )
A. B. C. D.
8.尽管目前人类还无法准确预报地震,但科学家通过研究,已经知道地震时释放出的能量E(单位:焦耳)与地震里氏震级M之间的关系为.2011年3月11日,日本东北部海域发生里氏9.0级地震,它所释放出来的能量大约是2022年1月2日在云南丽江市宁蒗县发生5.5级地震所释放能量的倍数为( )
A. B. C. D.
二、多选题
9.下列函数中,既是偶函数又存在零点的是( )
A. B. C. D.
10.已知函数,则( )
A.的定义域为 B.是偶函数
C.函数的零点为0 D.当时,的最大值为
11.如图,某池塘里的浮萍面积(单位:)与时间(单位:月)的关系式为且,.则下列说法正确的是( )
A.浮萍每月增加的面积都相等
B.第6个月时,浮萍的面积会超过
C.浮萍面积从蔓延到只需经过5个月
D.若浮萍面积蔓延到,,所经过的时间分别为,,,则
12.设函数则( )
A.当时,的值域为
B.当的单调递增区间为时,
C.当时,函数有2个零点
D.当时,关于x的方程有2个实数解
三、填空题
13.2021年8月30日第九届未来信息通信技术国际研讨会在北京开幕.研讨会聚焦于5G的持续创新和演进、信息通信的未来技术前瞻与发展、信息通信技术与其他前沿科技的融合创新.香农公式是被广泛公认的通信理论基础和研究依据,它表示在受噪声干扰的信道中,最大信息传递速率C取决于信道带宽W、信道内信号的平均功率S,信道内部的高斯噪声功率N的大小,其中叫作信噪比.若不改变信道带宽W,而将信噪比从11提升至499,则最大信息传递速率C大约会提升到原来的______倍(结果保留1位小数).(参考数据:,)
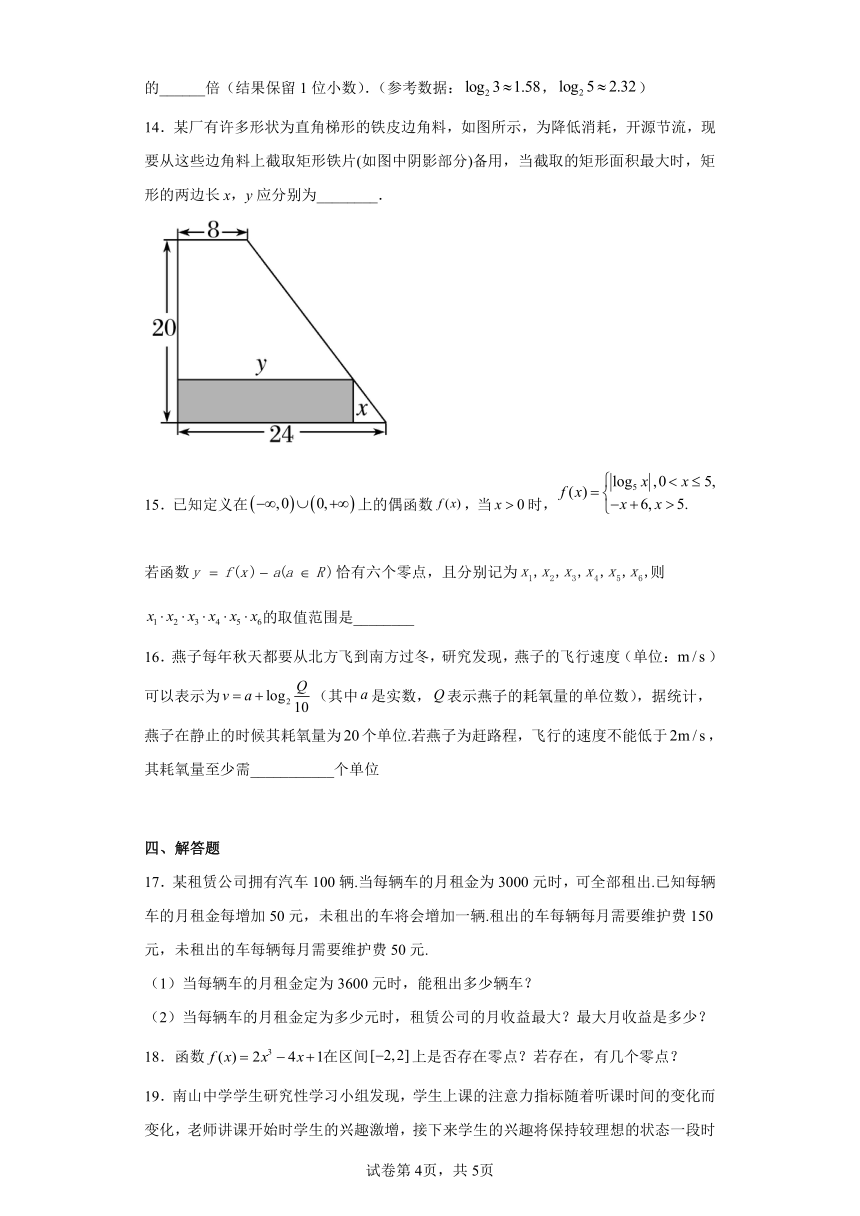
14.某厂有许多形状为直角梯形的铁皮边角料,如图所示,为降低消耗,开源节流,现要从这些边角料上截取矩形铁片(如图中阴影部分)备用,当截取的矩形面积最大时,矩形的两边长x,y应分别为________.
15.已知定义在上的偶函数,当时,若函数恰有六个零点,且分别记为则的取值范围是________
16.燕子每年秋天都要从北方飞到南方过冬,研究发现,燕子的飞行速度(单位:)可以表示为(其中是实数,表示燕子的耗氧量的单位数),据统计,燕子在静止的时候其耗氧量为个单位.若燕子为赶路程,飞行的速度不能低于,其耗氧量至少需___________个单位
四、解答题
17.某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.已知每辆车的月租金每增加50元,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
18.函数在区间上是否存在零点?若存在,有几个零点?
19.南山中学学生研究性学习小组发现,学生上课的注意力指标随着听课时间的变化而变化,老师讲课开始时学生的兴趣激增,接下来学生的兴趣将保持较理想的状态一段时间,随后学生的注意力开始分散.该小组发现注意力指标与上课时刻第分钟末的关系如下(,设上课开始时,.),.若上课后第分钟末时的注意力指标为.
(1)求的值;
(2)在一节课中,学生的注意力指标至少达到的时间能保持多长?
20.声强级(单位:dB)由公式给出,其中I为声强(单位:).
(1)一般正常人听觉能忍受的最高声强为,能听到的最低声强为.求人听觉的声强级范围.
(2)平时常人交谈时的声强约为,求其声强级.
21.某镇发展绿色经济,因地制宜将该乡镇打造成“特色农产品小镇”,根据研究发现:生产某农产品,固定投入万元,最大产量万斤,每生产万斤,需其他投入万元,,根据市场调查,该农产品售价每万斤万元,且所有产量都能全部售出.(利润收入成本)
(1)写出年利润(万元)与产量(万斤)的函数解析式;
(2)求年产量为多少万斤时,该镇所获利润最大?求出利润最大值.
22.2021年,小林经过市场调查,决定投资生产某种电子零件,已知固定成本为6万元,年流动成本(万元)与年产品产量x(万件)的关系为,每个电子零件售价为12元,若小林加工的零件能全部售完.
(1)求年利润(万元)关于年产量x(万件)的函数解析式;
(2)求当年产量x为多少万件时年利润最大?最大值是多少?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】算出第二天订单数,除以志愿者每天能完成的订单配货数即可.
【详解】由题意,第二天新增订单数为,
,故至少需要志愿者名.
故选:B
【点晴】本题主要考查函数模型的简单应用,属于基础题.
2.B
【分析】根据一元二次方程根的分布情况,列出不等式,求解即可.
【详解】根据题意不妨设函数的两个零点为,
要满足题意,则,,
解得.
故选:.
3.B
【解析】根据已知数据和函数关系式直接计算.
【详解】,
故选:B.
【点睛】本题考查函数的应用,属于基础题.
4.C
【分析】设装修电钻的声音强度为,普通室内谈话的声音强度为,由装修电钻的声音约为分贝,普通室内谈话的声音约为分贝,列出方程组解出,,可得出的值,得到答案.
【详解】设装修电钻的声音强度为,普通室内谈话的声音强度为,
由题意,,
所以装修电钻的声音强度和普通室内谈话的声音强度比值为
.
故选:C
【点睛】本题考查函数的实际应用问题,考查对数的性质、运算法则等基础知识,属于基础题.
5.D
【分析】根据函数的意义,结合一次函数,二次函数的性质作出函数图像,对选项一一分析即可.
【详解】由函数解析式作出函数图像如图所示,
讲授开始时,学生的兴趣递增;中间有段时间,学生的兴趣保持较理想的状态;随后学生的注意力开始分散,故A正确;
由,,知讲课开始后第5分钟比讲课开始第20分钟,学生的接受能力更强一点,故B正确;
讲课开始后第10分钟到第16分钟,达到最大值,此时学生的接受能力最强,故C正确;
对于D,当,解得或,
而,故学生的注意力达到55以上的情况下,不能讲完13分钟的题,故D错误.
故选:D
6.B
【分析】先利用特殊点求出函数解析式为,再利用指数函数的性质即可判断出正误.
【详解】解:图象可知,函数过点,
,
函数解析式为,
浮萍每月的增长率为,故选项A正确,
函数是指数函数,是曲线型函数,浮萍每月增加的面积不相等,故选项B错误,
当时,,故选项C正确,
对于D选项,,,,,
又,,故选项D正确,
故选:B.
7.A
【分析】利用初等函数的图像与性质以及图像的变换的知识进行判断.
【详解】对于A选项,函数在上是增函数且不存在零点,故A正确;
对于B选项,函数的零点是1,故B错误;
对于C选项,函数在上是减函数,故C错误;
对于D选项,函数在上是减函数,故D错误.
故选:A.
8.A
【分析】根据已知直接求出相应能量,然后可得.
【详解】设日本地震释放的能量为,云南地震释放的能量为,则,,所以.
故选:A
9.BD
【分析】利用偶函数与存在零点两个条件逐一判断各选项即可得解.
【详解】对于A,函数定义域为,该函数不是偶函数,A不是;
对于B,函数是R上的偶函数,由得或,即该函数有两个零点,B是;
对于C,函数是R上的奇函数,C不是;
对于D,是R上的偶函数,由得或,即该函数有两个零点,D是.
故选:BD
10.AD
【分析】根据函数的解析式,分别从定义域、奇偶性、零点、最值考察即可求解.
【详解】对A,由解析式可知的定义域为,故A正确;
对B,因为,可知是奇函数,故B不正确;
对C,,得,故C不正确;
对D, 当时,,当且仅当时取等号,
故D正确.
故选:AD
11.BCD
【分析】由题意结合函数图象可得,进而可得;由函数图象的类型可判断A;代入可判断B;代入、可判断C;代入、、,结合对数的运算法则即可得判断D;即可得解.
【详解】由题意可知,函数过点和点,则,
解得(负值舍去),
函数关系式为,
对于A,由函数是曲线型函数,所以浮萍每月增加的面积不相等,故选项A错误;
对于B,当时,,故选项B正确;
对于C,令得;令得,所以浮萍面积从增加到需要5个月,故选项C正确;
对于D,令得;令得;令得;
所以,故选项D正确.
故选:BCD.
【点睛】本题考查了函数解析式的确定及函数模型的应用,考查了运算求解能力,合理转化条件是解题关键,属于基础题.
12.AB
【分析】A选项,分情况讨论出的值域,B选项,分段函数单调性要满足的条件列出不等式,求出的取值范围;C选项,将零点问题转化为方程的解问题,求出;D选项,分段求出解的个数,得到答案.
【详解】当时,当时,,当时,单调递增,故,综上:的值域为,A正确;
的单调递增区间是和,因为的单调递增区间是,
所以,即,B正确;
当时,由,得,当时,令,得,此方程要有唯一解,得,即,C错误;
当时,令,即,解得:或,符合要求,令,解得:,符合要求,所以的图象与直线有3个交点,D错误.
故选:AB
13.2.5
【分析】设提升前最大信息传递速率为,提升后最大信息传递速率为,根据题意求出,再利用指数、对数的运算性质化简计算即可
【详解】设提升前最大信息传递速率为,提升后最大信息传递速率为,则由题意可知,,,
所以,
所以最大信息传递速率C会提升到原来的2.5倍.
故答案为:
14.15、12
【分析】先根据三角形的性质得出关系式,再根据面积关于的二次不等式求最值即可
【详解】由题干图知x,y满足关系式,
即,
矩形的面积,
故x=15,y=12时,S取最大值.
15.
【分析】根据题目条件,作出函数在上的图像,设,由对称性及对数运算知:,,故,根据求得范围.
【详解】根据题目条件,作出函数在上的图像,如图所示:
设的六个零点,自左到右为,则,
由对称性知:,又,
则,
故,
易知,则
故答案为:
16.80
【分析】根据给定条件求出常数a,再建立不等关系即可得解.
【详解】依题意,时,,于是得,解得,即,
由得:,即,解得,
所以其耗氧量至少需80个单位.
故答案为:80
17.(1)88辆车;(2)当每辆车的月租金定为4050元时,租赁公司的月收益最大,最大收益为307050元.
【分析】(1)根据每辆车的月租金每增加50元,未租出的车将会增加一辆可求出结果;
(2)根据题意求出租赁公司的月收益关于每辆车的月租金的函数解析式,再根据二次函数知识可求出结果.
【详解】(1)当每辆车的月租金定为3600元时,未租出的车辆数为,所以这时租出了88辆车.
(2)设每辆车的月租金定为x元,则租赁公司的月收益(单位:元)
,
整理得.
所以当时,最大,其最大值为.
所以当每辆车的月租金定为4050元时,租赁公司的月收益最大,最大收益为307050元.
18.存在,函数在区间上有三个零点.
【分析】借助于计算器首先考察区间的两个端点的函数值的符号是否相异,若为异号,则该区间上必有零点;若为同号,则再考察区间中间点的函数值的符号是否与区间两端点的函数值异号,经过几次这样的考察,即可得到本题的答案.
【详解】因为,,
所以在区间上至少有一个零点.
取区间的中点;
取区间的中点;
取区间的中点.
因为,所以在区间上至少有一个零点;
因为,所以在区间上至少有一个零点;
因为,所以在区间上至少有一个零点.
又由于函数是三次函数,最多有三个零点,
所以,函数在区间上有三个零点.
【点睛】本题考查零点存在性定理,利用二分法确定零点所在的区间,考查数形结合思想,属于基础题.
19.(1)
(2)
【分析】(1)由时对应的函数值为140,得的方程,解方程可得的值;
(2)根据题意当时可得,解不等式即可.
(1)
由题意得,
所以,则.
(2)
当时,由得.
则在一节课中,学生的注意力指标至少达到的时间能保持.
20.(1)(2)
【解析】(1)分别代入与求解即可.
(2)代入求解即可.
【详解】解:(1).
.
因此人听觉的声强级范围为.
(2).
【点睛】本题主要考查了对数的实际运用,需要根据题意代入对应的数值进行计算,属于基础题.
21.(1);
(2)当年产量为万斤时,该镇所获利润最大,最大利润为万元
【分析】(1)根据利润收入成本可得函数解析式;
(2)分别在和两种情况下,利用二次函数和对勾函数最值的求法可得结果.
【详解】(1)由题意得:;
(2)当时,,
则当时,;
当时,(当且仅当,即时取等号),;
,当,即年产量为万斤时,该镇所获利润最大,最大利润为万元.
22.(1);
(2)万件时最大利润为18万元.
【分析】(1)由题意,结合已知函数写出解析式;
(2)根据二次函数、对勾函数分别求出、上对应的利润最大值,比较它们的大小,即可确定最大年利润及对应的年产量.
(1)
由题设,,
所以.
(2)
当时,
故时最大利润为12万元;
当时,
当且仅当时等号成立,此时最大利润为18万元;
综上,当万件时最大利润为18万元.
答案第1页,共2页
答案第1页,共2页
1.在新冠肺炎疫情防控期间,某超市开通网上销售业务,每天能完成1200份订单的配货,由于订单量大幅增加,导致订单积压.为解决困难,许多志愿者踊跃报名参加配货工作.已知该超市某日积压500份订单未配货,预计第二天的新订单超过1600份的概率为0.05,志愿者每人每天能完成50份订单的配货,为使第二天完成积压订单及当日订单的配货的概率不小于0.95,则至少需要志愿者( )
A.10名 B.18名 C.24名 D.32名
2.设为实数,已知函数的两个零点在区间内,则的取值范围是( )
A. B.
C. D.
3.2020年6月17日15时19分,星期三,酒泉卫星发射中心,我国成功发射长征二号丁运载火箭,并成功将高分九号03星、皮星三号A星和德五号卫星送入预定轨道,携三星入轨,全程发射获得圆满成功,祖国威武.已知火箭的最大速度v(单位:)和燃料质量M(单位:),火箭质量m(单位:)的函数关系是:,若已知火箭的质量为3100公斤,燃料质量为310吨,则此时v的值为多少(参考数值为;)( )
A.13.8 B.9240 C.9.24 D.1380
4.当强度为x的声音对应的等级为分贝时,有(其中为常数).装修电钻的声音约为分贝,普通室内谈话的声音约为分贝.则装修电钻的声音强度与普通室内谈话的声音强度的比值为( )
A. B. C. D.
5.通过研究学生的学习行为,心理学家发现,学生的接受能力依赖于老师引入概念和描述所用的时间.若用表示学生掌握和接受概念的能力(越大,表示学生的接受能力越强),表示提出和讲授概念的时间(单位:),长期的实验和分析表明,与有以下关系:则下列说法错误的是( )
A.讲授开始时,学生的兴趣递增;中间有段时间,学生的兴趣保持较理想的状态;随后学生的注意力开始分散
B.讲课开始后第5分钟比讲课开始第20分钟,学生的接受能力更强一点
C.讲课开始后第10分钟到第16分钟,学生的接受能力最强
D.需要13分钟讲解的复杂问题,老师可以在学生的注意力至少达到55以上的情况下完成
6.如图,某池塘里浮萍的面积(单位:)与时间t(单位:月)的关系为,关于下列说法不正确的是( )
A.浮萍每月的增长率为2
B.浮萍每月增加的面积都相等
C.第4个月时,浮萍面积超过
D.若浮萍蔓延到所经过的时间分别是,、,则
7.给出下列函数,其中在上是增函数且不存在零点的函数的是( )
A. B. C. D.
8.尽管目前人类还无法准确预报地震,但科学家通过研究,已经知道地震时释放出的能量E(单位:焦耳)与地震里氏震级M之间的关系为.2011年3月11日,日本东北部海域发生里氏9.0级地震,它所释放出来的能量大约是2022年1月2日在云南丽江市宁蒗县发生5.5级地震所释放能量的倍数为( )
A. B. C. D.
二、多选题
9.下列函数中,既是偶函数又存在零点的是( )
A. B. C. D.
10.已知函数,则( )
A.的定义域为 B.是偶函数
C.函数的零点为0 D.当时,的最大值为
11.如图,某池塘里的浮萍面积(单位:)与时间(单位:月)的关系式为且,.则下列说法正确的是( )
A.浮萍每月增加的面积都相等
B.第6个月时,浮萍的面积会超过
C.浮萍面积从蔓延到只需经过5个月
D.若浮萍面积蔓延到,,所经过的时间分别为,,,则
12.设函数则( )
A.当时,的值域为
B.当的单调递增区间为时,
C.当时,函数有2个零点
D.当时,关于x的方程有2个实数解
三、填空题
13.2021年8月30日第九届未来信息通信技术国际研讨会在北京开幕.研讨会聚焦于5G的持续创新和演进、信息通信的未来技术前瞻与发展、信息通信技术与其他前沿科技的融合创新.香农公式是被广泛公认的通信理论基础和研究依据,它表示在受噪声干扰的信道中,最大信息传递速率C取决于信道带宽W、信道内信号的平均功率S,信道内部的高斯噪声功率N的大小,其中叫作信噪比.若不改变信道带宽W,而将信噪比从11提升至499,则最大信息传递速率C大约会提升到原来的______倍(结果保留1位小数).(参考数据:,)
14.某厂有许多形状为直角梯形的铁皮边角料,如图所示,为降低消耗,开源节流,现要从这些边角料上截取矩形铁片(如图中阴影部分)备用,当截取的矩形面积最大时,矩形的两边长x,y应分别为________.
15.已知定义在上的偶函数,当时,若函数恰有六个零点,且分别记为则的取值范围是________
16.燕子每年秋天都要从北方飞到南方过冬,研究发现,燕子的飞行速度(单位:)可以表示为(其中是实数,表示燕子的耗氧量的单位数),据统计,燕子在静止的时候其耗氧量为个单位.若燕子为赶路程,飞行的速度不能低于,其耗氧量至少需___________个单位
四、解答题
17.某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.已知每辆车的月租金每增加50元,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
18.函数在区间上是否存在零点?若存在,有几个零点?
19.南山中学学生研究性学习小组发现,学生上课的注意力指标随着听课时间的变化而变化,老师讲课开始时学生的兴趣激增,接下来学生的兴趣将保持较理想的状态一段时间,随后学生的注意力开始分散.该小组发现注意力指标与上课时刻第分钟末的关系如下(,设上课开始时,.),.若上课后第分钟末时的注意力指标为.
(1)求的值;
(2)在一节课中,学生的注意力指标至少达到的时间能保持多长?
20.声强级(单位:dB)由公式给出,其中I为声强(单位:).
(1)一般正常人听觉能忍受的最高声强为,能听到的最低声强为.求人听觉的声强级范围.
(2)平时常人交谈时的声强约为,求其声强级.
21.某镇发展绿色经济,因地制宜将该乡镇打造成“特色农产品小镇”,根据研究发现:生产某农产品,固定投入万元,最大产量万斤,每生产万斤,需其他投入万元,,根据市场调查,该农产品售价每万斤万元,且所有产量都能全部售出.(利润收入成本)
(1)写出年利润(万元)与产量(万斤)的函数解析式;
(2)求年产量为多少万斤时,该镇所获利润最大?求出利润最大值.
22.2021年,小林经过市场调查,决定投资生产某种电子零件,已知固定成本为6万元,年流动成本(万元)与年产品产量x(万件)的关系为,每个电子零件售价为12元,若小林加工的零件能全部售完.
(1)求年利润(万元)关于年产量x(万件)的函数解析式;
(2)求当年产量x为多少万件时年利润最大?最大值是多少?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】算出第二天订单数,除以志愿者每天能完成的订单配货数即可.
【详解】由题意,第二天新增订单数为,
,故至少需要志愿者名.
故选:B
【点晴】本题主要考查函数模型的简单应用,属于基础题.
2.B
【分析】根据一元二次方程根的分布情况,列出不等式,求解即可.
【详解】根据题意不妨设函数的两个零点为,
要满足题意,则,,
解得.
故选:.
3.B
【解析】根据已知数据和函数关系式直接计算.
【详解】,
故选:B.
【点睛】本题考查函数的应用,属于基础题.
4.C
【分析】设装修电钻的声音强度为,普通室内谈话的声音强度为,由装修电钻的声音约为分贝,普通室内谈话的声音约为分贝,列出方程组解出,,可得出的值,得到答案.
【详解】设装修电钻的声音强度为,普通室内谈话的声音强度为,
由题意,,
所以装修电钻的声音强度和普通室内谈话的声音强度比值为
.
故选:C
【点睛】本题考查函数的实际应用问题,考查对数的性质、运算法则等基础知识,属于基础题.
5.D
【分析】根据函数的意义,结合一次函数,二次函数的性质作出函数图像,对选项一一分析即可.
【详解】由函数解析式作出函数图像如图所示,
讲授开始时,学生的兴趣递增;中间有段时间,学生的兴趣保持较理想的状态;随后学生的注意力开始分散,故A正确;
由,,知讲课开始后第5分钟比讲课开始第20分钟,学生的接受能力更强一点,故B正确;
讲课开始后第10分钟到第16分钟,达到最大值,此时学生的接受能力最强,故C正确;
对于D,当,解得或,
而,故学生的注意力达到55以上的情况下,不能讲完13分钟的题,故D错误.
故选:D
6.B
【分析】先利用特殊点求出函数解析式为,再利用指数函数的性质即可判断出正误.
【详解】解:图象可知,函数过点,
,
函数解析式为,
浮萍每月的增长率为,故选项A正确,
函数是指数函数,是曲线型函数,浮萍每月增加的面积不相等,故选项B错误,
当时,,故选项C正确,
对于D选项,,,,,
又,,故选项D正确,
故选:B.
7.A
【分析】利用初等函数的图像与性质以及图像的变换的知识进行判断.
【详解】对于A选项,函数在上是增函数且不存在零点,故A正确;
对于B选项,函数的零点是1,故B错误;
对于C选项,函数在上是减函数,故C错误;
对于D选项,函数在上是减函数,故D错误.
故选:A.
8.A
【分析】根据已知直接求出相应能量,然后可得.
【详解】设日本地震释放的能量为,云南地震释放的能量为,则,,所以.
故选:A
9.BD
【分析】利用偶函数与存在零点两个条件逐一判断各选项即可得解.
【详解】对于A,函数定义域为,该函数不是偶函数,A不是;
对于B,函数是R上的偶函数,由得或,即该函数有两个零点,B是;
对于C,函数是R上的奇函数,C不是;
对于D,是R上的偶函数,由得或,即该函数有两个零点,D是.
故选:BD
10.AD
【分析】根据函数的解析式,分别从定义域、奇偶性、零点、最值考察即可求解.
【详解】对A,由解析式可知的定义域为,故A正确;
对B,因为,可知是奇函数,故B不正确;
对C,,得,故C不正确;
对D, 当时,,当且仅当时取等号,
故D正确.
故选:AD
11.BCD
【分析】由题意结合函数图象可得,进而可得;由函数图象的类型可判断A;代入可判断B;代入、可判断C;代入、、,结合对数的运算法则即可得判断D;即可得解.
【详解】由题意可知,函数过点和点,则,
解得(负值舍去),
函数关系式为,
对于A,由函数是曲线型函数,所以浮萍每月增加的面积不相等,故选项A错误;
对于B,当时,,故选项B正确;
对于C,令得;令得,所以浮萍面积从增加到需要5个月,故选项C正确;
对于D,令得;令得;令得;
所以,故选项D正确.
故选:BCD.
【点睛】本题考查了函数解析式的确定及函数模型的应用,考查了运算求解能力,合理转化条件是解题关键,属于基础题.
12.AB
【分析】A选项,分情况讨论出的值域,B选项,分段函数单调性要满足的条件列出不等式,求出的取值范围;C选项,将零点问题转化为方程的解问题,求出;D选项,分段求出解的个数,得到答案.
【详解】当时,当时,,当时,单调递增,故,综上:的值域为,A正确;
的单调递增区间是和,因为的单调递增区间是,
所以,即,B正确;
当时,由,得,当时,令,得,此方程要有唯一解,得,即,C错误;
当时,令,即,解得:或,符合要求,令,解得:,符合要求,所以的图象与直线有3个交点,D错误.
故选:AB
13.2.5
【分析】设提升前最大信息传递速率为,提升后最大信息传递速率为,根据题意求出,再利用指数、对数的运算性质化简计算即可
【详解】设提升前最大信息传递速率为,提升后最大信息传递速率为,则由题意可知,,,
所以,
所以最大信息传递速率C会提升到原来的2.5倍.
故答案为:
14.15、12
【分析】先根据三角形的性质得出关系式,再根据面积关于的二次不等式求最值即可
【详解】由题干图知x,y满足关系式,
即,
矩形的面积,
故x=15,y=12时,S取最大值.
15.
【分析】根据题目条件,作出函数在上的图像,设,由对称性及对数运算知:,,故,根据求得范围.
【详解】根据题目条件,作出函数在上的图像,如图所示:
设的六个零点,自左到右为,则,
由对称性知:,又,
则,
故,
易知,则
故答案为:
16.80
【分析】根据给定条件求出常数a,再建立不等关系即可得解.
【详解】依题意,时,,于是得,解得,即,
由得:,即,解得,
所以其耗氧量至少需80个单位.
故答案为:80
17.(1)88辆车;(2)当每辆车的月租金定为4050元时,租赁公司的月收益最大,最大收益为307050元.
【分析】(1)根据每辆车的月租金每增加50元,未租出的车将会增加一辆可求出结果;
(2)根据题意求出租赁公司的月收益关于每辆车的月租金的函数解析式,再根据二次函数知识可求出结果.
【详解】(1)当每辆车的月租金定为3600元时,未租出的车辆数为,所以这时租出了88辆车.
(2)设每辆车的月租金定为x元,则租赁公司的月收益(单位:元)
,
整理得.
所以当时,最大,其最大值为.
所以当每辆车的月租金定为4050元时,租赁公司的月收益最大,最大收益为307050元.
18.存在,函数在区间上有三个零点.
【分析】借助于计算器首先考察区间的两个端点的函数值的符号是否相异,若为异号,则该区间上必有零点;若为同号,则再考察区间中间点的函数值的符号是否与区间两端点的函数值异号,经过几次这样的考察,即可得到本题的答案.
【详解】因为,,
所以在区间上至少有一个零点.
取区间的中点;
取区间的中点;
取区间的中点.
因为,所以在区间上至少有一个零点;
因为,所以在区间上至少有一个零点;
因为,所以在区间上至少有一个零点.
又由于函数是三次函数,最多有三个零点,
所以,函数在区间上有三个零点.
【点睛】本题考查零点存在性定理,利用二分法确定零点所在的区间,考查数形结合思想,属于基础题.
19.(1)
(2)
【分析】(1)由时对应的函数值为140,得的方程,解方程可得的值;
(2)根据题意当时可得,解不等式即可.
(1)
由题意得,
所以,则.
(2)
当时,由得.
则在一节课中,学生的注意力指标至少达到的时间能保持.
20.(1)(2)
【解析】(1)分别代入与求解即可.
(2)代入求解即可.
【详解】解:(1).
.
因此人听觉的声强级范围为.
(2).
【点睛】本题主要考查了对数的实际运用,需要根据题意代入对应的数值进行计算,属于基础题.
21.(1);
(2)当年产量为万斤时,该镇所获利润最大,最大利润为万元
【分析】(1)根据利润收入成本可得函数解析式;
(2)分别在和两种情况下,利用二次函数和对勾函数最值的求法可得结果.
【详解】(1)由题意得:;
(2)当时,,
则当时,;
当时,(当且仅当,即时取等号),;
,当,即年产量为万斤时,该镇所获利润最大,最大利润为万元.
22.(1);
(2)万件时最大利润为18万元.
【分析】(1)由题意,结合已知函数写出解析式;
(2)根据二次函数、对勾函数分别求出、上对应的利润最大值,比较它们的大小,即可确定最大年利润及对应的年产量.
(1)
由题设,,
所以.
(2)
当时,
故时最大利润为12万元;
当时,
当且仅当时等号成立,此时最大利润为18万元;
综上,当万件时最大利润为18万元.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
