2022——2023高一数学期末考试章章通关练——第七章 概率1(含解析)
文档属性
| 名称 | 2022——2023高一数学期末考试章章通关练——第七章 概率1(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 613.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-19 09:38:04 | ||
图片预览




文档简介
一、单选题
1.若随机事件,互斥,,发生的概率均不等于0,且,,则实数的取值范围是( )
A. B. C. D.
2.如图,“红旗-9”在国内外都被认为属于第三代防空导弹系统,其杀伤空域大,抗干扰和抗多目标饱和攻击能力强,导引系统先进(有两级指挥管制体制),最高速度4.2马赫,最大射程为200公里,射高0.5至30公里,主要攻击高空敌机或导弹,是我国高空防空导弹的杰出代表.现假设在一次实战对抗演习中,单发红旗-9防空导弹对敌方高速飞行器的拦截成功率为0.8,则两发齐射(是否成功拦截互不干扰),敌方高速飞行器被拦截的概率为( )
A.0.96 B.0.88 C.1.6 D.0.64
3.某中学的学生积极参加体育锻炼,其中有96%的学生喜欢足球或游泳,60%的学生喜欢足球,82%的学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是( )
A.62% B.56%
C.46% D.42%
4.抛掷两枚均匀的骰子,记录正面朝上的点数,则下列选项的两个事件中,互斥但不对立的是( )
A.事件“点数之和为奇数”与事件“点数之和为9”
B.事件“点数之和为偶数”与事件“点数之和为奇数”
C.事件“点数之和为6”与事件“点数之和为9”
D.事件“点数之和不小于9”与事件“点数之和小于等于8”
5.某大学进行“羽毛球”、“美术”、“音乐”三个社团选拔.某同学经过考核选拔通过该校的“羽毛球”“美术”、“音乐”三个社团的概率依次为,已知三个社团中他恰好能进入两个的概率为,假设该同学经过考核通过这三个社团选拔成功与否相互独立,则该同学一个社团都不能进入的概率为( )
A. B. C. D.
6.下列各对事件中,不互为相互独立事件的是( )
A.掷一枚骰子一次,事件“出现偶数点”;事件“出现3点或6点”
B.袋中有3白、2黑共5个大小相同的小球,依次有放回地摸两球,事件“第一次摸到白球”,事件“第二次摸到白球”
C.袋中有3白、2黑共5个大小相同的小球,依次不放回地摸两球,事件“第一次摸到白球”,事件“第二次摸到黑球”
D.甲组3名男生,2名女生;乙组2名男生,3名女生,现从甲、乙两组中各选1名同学参加演讲比赛,事件“从甲组中选出1名男生”,事件“从乙组中选出1名女生”
7.若连续抛掷两次质地均匀的骰子,得到的点数分别为m,n,则满足的概率是( )
A. B. C. D.
8.某学校共有教职工120人,对他们进行年龄结构和受教育程度的调查,其结果如下表:
本科 研究生 合计
35岁以下 40 30 70
35-50岁 27 13 40
50岁以上 8 2 10
现从该校教职工中任取1人,则下列结论正确的是( )A.该教职工具有本科学历的概率低于60%
B.该教职工具有研究生学历的概率超过50%
C.该教职工的年龄在50岁以上的概率超过10%
D.该教职工的年龄在35岁及以上且具有研究生学历的概率超过10%
二、多选题
9.下列有关古典概型的说法中,正确的是( )
A.试验的样本空间的样本点总数有限
B.每个事件出现的可能性相等
C.每个样本点出现的可能性相等
D.已知样本点总数为,若随机事件包含个样本点,则事件发生的概率
10.抛掷两枚质地均匀的骰子,记“第一枚骰子出现的点数小于3”为事件A,“第二枚骰子出现的点数不小于3”为事件B,则下列结论中正确的是( )
A.事件A与事件B互为对立事件
B.事件A与事件B相互独立
C.
D.
11.下列说法中正确的有( )
A.若事件A与事件B是互斥事件,则
B.若事件A与事件B是对立事件,则
C.某人打靶时连续射击三次,则事件“至少有两次中靶”与事件“至多有一次中靶”是对立事件
D.把红、橙、黄3张纸牌随机分给甲、乙、丙3人,每人分得1张,则事件“甲分得的不是红牌”与事件“乙分得的不是红牌”是互斥事件
12.下列说法错误的是( )
A.随着试验次数的增大,随机事件发生的频率会逐渐稳定于该随机事件发生的概率
B.某种福利彩票的中奖概率为,买1000张这种彩票一定能中奖
C.连续100次掷一枚硬币,结果出现了49次反面,则掷一枚硬币出现反面的概率为
D.某市气象台预报“明天本市降水概率为70%”,指的是:该市气象台专家中,有70%认为明天会降水,30%认为明天不会降水
三、填空题
13.甲、乙两人进行乒乓球比赛,比赛规则为“三局两胜制”(即先赢两局者为胜,若前两局某人连胜,则无需比第三局),根据以往两人的比赛数据分析,甲在每局比赛中获胜的概率为,则本次比赛中甲获胜的概率为___________.
14.已知小张每次射击命中十环的概率都为40%,现采用随机模拟的方法估计小张三次射击恰有两次命中十环的概率,先由计算器产生0到9之间取整数值的随机数,指定2,4,6,8表示命中十环,0,1,3,5,7,9表示未命中十环,再以每三个随机数为一组,代表三次射击的结果,经随机模拟产生了如下20组随机数:据此估计,小张三次射击恰有两次命中十环的概率约为__________.
15.连续掷一颗骰子两次,事件“向上的点数之和为”相对应的基本事件空间是____________________.
16.已知甲、乙两名篮球运动员投篮投中的概率分别为0.5和0.8,且甲、乙两人投篮的结果互不影响.若甲、乙两人各投篮一次,则至少有一人投中的概率为_____.
四、解答题
17.某种婴儿用品主要材质是橡胶,在加工过程中,可能会残留一些未挥发完全的溶剂,以及橡胶本身含有的化合物等,长期潜伏积累,对免疫力尚未健全的婴幼儿会危害甚大,为了测量此类新产品的挥发性物质含量,从生产的产品中随机抽取100个,得到如下频率分布直方图,若以频率作为概率,规定该婴儿用品的挥发性物质含量<18‰为合格产品.
(1)若这100个产品的挥发性物质含量的平均值大于16,则需进行技术改进,试问该新产品是否需要技术改进?
(2)为了解产品不合格的原因,用分层抽样的方法从与中抽取6个进行分析,然后从这6个中抽取2个进一步实验,求2个均在内的概率.
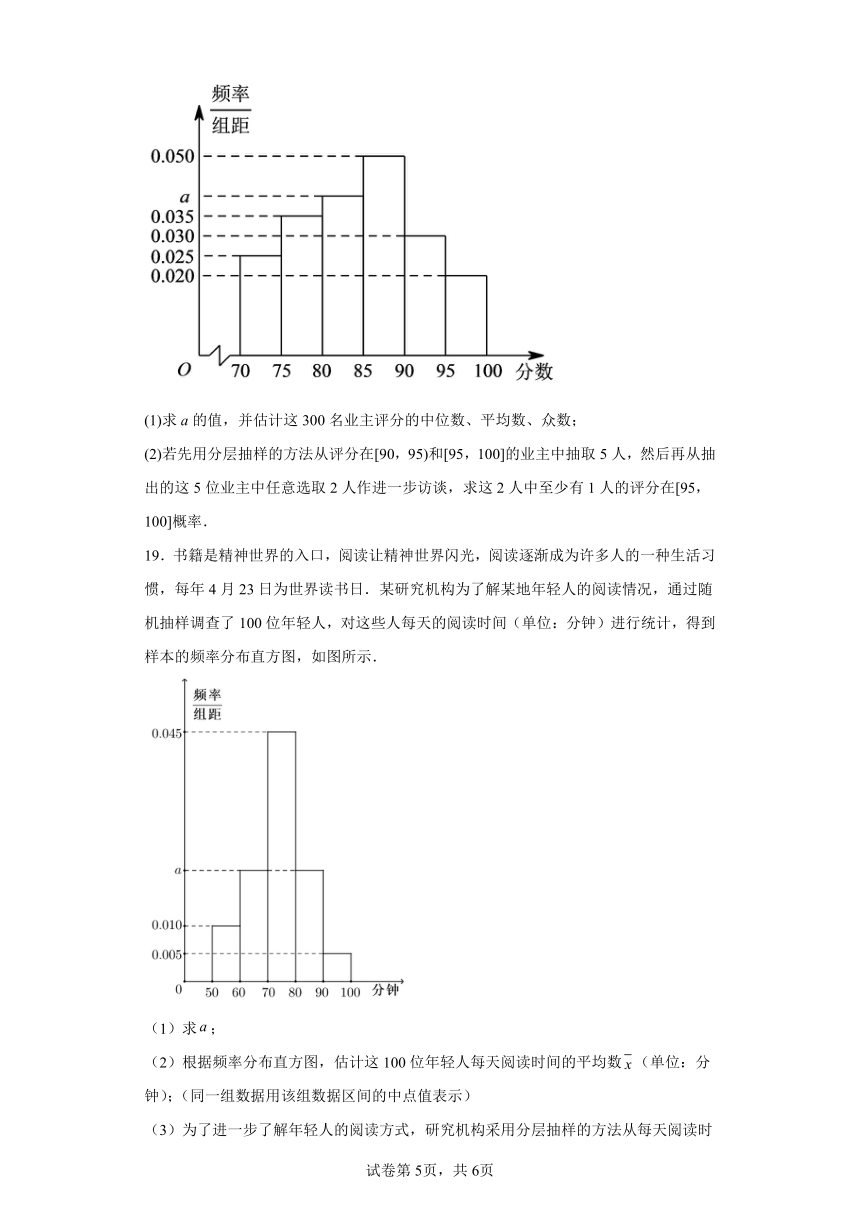
18.“2021年全国城市节约用水宣传周”已于5月9日至15日举行.成都市围绕“贯彻新发展理念,建设节水型城市”这一主题,开展了形式多样,内容丰富的活动,进一步增强全民保护水资源,防治水污染,节约用水的意识.为了解活动开展成效,某街道办事处工作人员赴一小区调查住户的节约用水情况,随机抽取了300名业主进行节约用水调查评分,将得到的分数分成6组:[70,75),[75,80),[80,85),[85,90),[90,95),[95,100],得到如图所示的频率分布直方图.
(1)求a的值,并估计这300名业主评分的中位数、平均数、众数;
(2)若先用分层抽样的方法从评分在[90,95)和[95,100]的业主中抽取5人,然后再从抽出的这5位业主中任意选取2人作进一步访谈,求这2人中至少有1人的评分在[95,100]概率.
19.书籍是精神世界的入口,阅读让精神世界闪光,阅读逐渐成为许多人的一种生活习惯,每年4月23日为世界读书日.某研究机构为了解某地年轻人的阅读情况,通过随机抽样调查了100位年轻人,对这些人每天的阅读时间(单位:分钟)进行统计,得到样本的频率分布直方图,如图所示.
(1)求;
(2)根据频率分布直方图,估计这100位年轻人每天阅读时间的平均数(单位:分钟);(同一组数据用该组数据区间的中点值表示)
(3)为了进一步了解年轻人的阅读方式,研究机构采用分层抽样的方法从每天阅读时间位于分组,和的年轻人中抽取5人,再从中任选2人进行调查,求其中至少有1人每天阅读时间位于的概率.
20.掷一个骰子,下列事件:,,,,.求:
(1), ;
(2),;
(3)记是事件的对立事件,求,,,.
21.某车间共有八名工人,为了保障安全生产,每月1号要从中选取四名工人参加同样的技能测试,每名工人通过每次测试的概率都是.甲从事的岗位比较特殊,每次他都必须参加技能测试.工厂规定:若工人连续两次没通过测试,则被撤销上岗资格.求甲恰好参加四次技能测试后被撤销上岗资格的概率.
22.在2016珠海航展志愿服务开始前,团珠海市委调查了北京师范大学珠海分校某班50名志愿者参加志愿服务礼仪培训和赛会应急救援培训的情况,数据如下表:单位:人
参加志愿服务礼仪培训 未参加志愿服务礼仪培训
参加赛会应急救援培训 8 8
未参加赛会应急救援培训 4 30
(1)从该班随机选1名同学,求该同学至少参加上述一个培训的概率;
(2)在既参加志愿服务礼仪培训又参加赛会应急救援培训的8名同学中,有5名男同学A,A,A,A,A名女同学B,B,B现从这5名男同学和3名女同学中各随机选1人,求A被选中且B未被选中的概率.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】利用互斥事件的加法公式及概率的基本性质列式即可作答.
【详解】因随机事件,互斥,则,
依题意及概率的性质得,即,解得,
所以实数的取值范围是.
故选:C
2.A
【分析】根据对立事件及相互独立事件的概率公式计算可得;
【详解】解:依题意敌方高速飞行器被拦截的概率为
故选:A
3.C
【分析】记“该中学学生喜欢足球”为事件,“该中学学生喜欢游泳”为事件,则“该中学学生喜欢足球或游泳”为事件,“该中学学生既喜欢足球又喜欢游泳”为事件,然后根据积事件的概率公式可得结果.
【详解】记“该中学学生喜欢足球”为事件,“该中学学生喜欢游泳”为事件,则“该中学学生喜欢足球或游泳”为事件,“该中学学生既喜欢足球又喜欢游泳”为事件,
则,,,
所以
所以该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例为.
故选:C.
【点睛】本题考查了积事件的概率公式,属于基础题.
4.C
【分析】利用对立事件、互斥事件的定义直接求解.
【详解】对于,二者能同时发生,不是互斥事件,故错误;
对于,二者不能同时发生,也不能同时不发生,是对立事件,故错误;
对于,二者不能同时发生,但能同时不发生,是互斥但不对立事件,故正确;
对于,二者不能同时发生,也不能同时不发生,是对立事件,故错误.
故选:.
5.D
【分析】根据互相独立事件的概率公式计算可得;
【详解】解:由题知,三个社团中他恰好能进入两个的概率为,则,所以,所以,所以该同学一个社团都不进入的概率.
故选:D.
6.C
【分析】利用对立事件和相互独立事件的概念求解.
【详解】解:对于选项A,事件,事件,事件,基本事件空间,所以,,,即,因此事件与事件N是相互独立事件;
对于选项B,袋中有3白、2黑共5个大小相同的小球,依次有放回地摸两球,事件“第一次摸到白球”,事件“第二次摸到白球”, 则事件发生与否与无关,同时,事件发生与否与无关,则事件与事件是相互独立事件;
对于选项C,袋中有3白、2黑,5个大小相同的小球,依次不放回地摸两球, 事件“第一次摸到白球”,事件“第二次摸到黑球”, 则事件发生与否和事件有关,故事件和事件与不是相互独立事件;
对于选项D,甲组3名男生,2名女生;乙组2名男生,3名女生,现从甲、乙两组中各选1名同学参加演讲比赛,事件“从甲组中选出1名男生”,事件“从乙组中选出1名女生”,则事件发生与否与无关,同时,事件发生与否与无关,则事件与事件是相互独立事件;
故选:C.
7.B
【分析】利用列举法列出所有可能结果,再根据古典概型的概率公式计算可得.
【详解】解:设连续投掷两次骰子,得到的点数依次为、,两次抛掷得到的结果可以用表示,
则结果有,,,,,,
,,,,,,
,,,,,,
,,,,,,
,,,,,,
,,,,,,
共有36种.
其中满足有:,,,,,,,,,,,,,共种,
所以满足的概率.
故选:B
8.D
【分析】根据表中数据,用频率代替概率求解.
【详解】A.该教职工具有本科学历的概率 ,故错误;
B.该教职工具有研究生学历的概率,故错误;
C.该教职工的年龄在50岁以上的概率,故错误;
D.该教职工的年龄在35岁及以上且具有研究生学历的概率,故正确.
【点睛】本题主要考查概率的求法,还考查了分析求解问题的能力,属于基础题.
9.ACD
【分析】根据古典概型的定义逐项判断即可.
【详解】由古典概型概念可知:试验的样本空间的样本点总数有限;每个样本点出现的可能性相等.
故AC正确;每个事件不一定是样本点,可能包含若干个样本点,所以B不正确;
根据古典概型的概率计算公式可知D正确.
故选:ACD
10.BCD
【分析】利用对立事件的意义判断A;利用相互独立事件的定义判断B;由事件A,B的概率计算判断C,D作答.
【详解】依题意,第一枚骰子出现的点数小于3与第二枚骰子出现的点数不小于3可以同时发生,
即事件A与事件B不互斥,则事件A与事件B不是对立事件,A不正确;
显然有,
抛掷两枚质地均匀的骰子的试验的所有结果:
,共36个,它们等可能,
事件AB所含的结果有:,共8个,
则有,即事件A与事件B相互独立,B正确;
显然,,C,D都正确.
故选:BCD
11.ABC
【分析】根据互斥事件、对立事件的概念判断即可.
【详解】解:事件与事件互斥,则不可能同时发生,所以,故A正确;
事件与事件是对立事件,则事件即为事件,所以,故B正确;
事件“至少两次中靶”与“至多一次中靶”不可能同时发生,且二者必发生其一,所以为对立事件,故C正确;
“甲分得的不是红牌”与事件“乙分得的不是红牌”可能同时发生,即“丙分得的是红牌”,所以不是互斥事件,故D错误.
故选:ABC
12.BCD
【分析】根据概率的定义和生活中的概率判断各选项的对错.
【详解】由频率和概率的关系可知随着试验次数的增大,随机事件发生的频率会逐渐稳定于该随机事件发生的概率,A正确,
某种福利彩票的中奖概率为,买1000张这种彩票不一定能中奖,B错误,
掷一枚硬币出现反面的概率为,C错误,
某市气象台预报“明天本市降水概率为70%”,指的是明天有70%的可能会降水,D错误,
故选:BCD.
13.
【分析】根据题意,利用相互独立事件的概率乘法公式分别求得甲前两局获胜的概率和前两局中一胜一负,第三局胜利的概率,结合互斥事件的概率加法公式,即可求解.
【详解】因为甲在每局比赛中获胜的概率为,
若甲前两局获胜,其概率为;
若甲前两局中一胜一负,第三局胜利,其概率为,
所以本次比赛中甲获胜的概率为.
故答案为:.
14.0.3
【分析】确定随机数组中以恰有两个数字是2,4,6,8,再由概率公式计算.
【详解】由题意,随机数组421,292,274,632,478,663共6个,表示恰有两次命中十环,
所以概率为.
故答案为:0.3.
15.
【分析】用列举法可得出两次点数之和为包含的基本事件.
【详解】将一颗骰子先后抛掷两次,观察向上的点数,
基本事件总数,
两次点数之和为包含的基本事件有:
故答案为:
16.0.9
【分析】根据对立事件的概率公式即可求出.
【详解】设“甲、乙两人各投篮一次,则至少有一人投中”,
则.
故答案为:0.9.
17.(1)该产品需要进行技术改进;(2).
【分析】(1)、由频率分布直方图求出平均值判断与16的大小关系即可得出结论;
(2)、先根据分层抽样求得在与中所抽取的个数,运用列举法列出事件的所有情况,由古典概率公式可求得答案.
【详解】(1)∵,故该产品需要进行技术改进;
(2)组的产品的个数为,组的产品的个数,所以从组中抽取个,从组中抽取个,
记组中抽取的5个分别为,组中抽取的一个为,
则从6个中抽取2个的所有情况如下:共15种情况,
其中在中恰有2个的有共10种情况,所以所求的概率.
18.(1),中位数为85,平均数为84.625,众数为87.5
(2)
【分析】(1)由频率分布直方图的的性质,所有小矩形的面积之和为1,可解得的值,由中位数的定义,找到频率之和为的点,平均数的估计值公式为每个小矩形的中点值与对应小矩形面积的乘积之和,众数估计值为最高小矩形的中点;
(2)首先根据两个分组的人数之比,采用分层抽样的方法,得到每个分组抽取的人数,则采用列举法,罗列多有情况和符合题意的情况,根据古典概型的概率计算公式得到答案.
(1)
∵第三组的频率为1-(0.020+0.025+0.030+0.035+0.050)×5=0.200,
又第一组的频率为0.025×5=0.125,第二组的频率为0.035×5=0.175,
第三组的频率为0.200.∵前三组的频率之和为0.125+0.175+0.200=0.500,
∴这300名业主评分的中位数为85.
平均数为72.5×0.025×5+77.5×0.035×5+82.5×0.040×5+87.5×0.050×5+92.5×0.030×5+97.5×0.020×5=84.625.
众数为(85+90)÷2=87.5.
(2)
由频率分布直方图,知评分在[90,95)的人数与评分在[95,100]的人数的比值为3:2.
∴采用分层抽样法抽取5人,评分在[90,95)的有3人,评分在[95,100]有2人.
不妨设评分在[90,95)的3人分别为;评分在[95,100]的2人分别为.
则从5人中任选2人的所有可能情况有:
{A1,A2},{A1,A3},{A1,B1},{A1,B2},{A2,A3},{A2,B1},{A2,B2},{A3,B1},{A3,B2},{B1,B2},共10种.
其中选取的2人中至少有1人的评分在[95,100]的情况有:
{A1,B1},{A1,B2},{A2,B1},{A2,B2},{A3,B1},{A3,B2},{B1,B2},共7种.
故这2人中至少有1人的评分在[95,100]的概率为.
19.(1);(2)74;(3).
【分析】(1)利用小矩形的面积之和等于即可求解.
(2)根据频率分布直方图,由小矩形底边中点横坐标与小矩形面积乘积之和即可求解.
(3)根据频率分布直方图得出频率比,从中任选2人列出基本事件个数,根据古典概型的概率计算公式即可求解.
【详解】解:(1)根据频率分布直方图得:
(2)根据频率分布直方图得:
,
(3)由于,和的频率之比为:1∶2∶2,
故抽取的5人中,和分别为:1人,2人,2人,
记的1人为,的2人为,,的2人为,
故随机抽取2人共有,,,,,,
,,,10种,
其中至少有1人每天阅读时间位于的包含7种,
故概率.
20.(1),.
(2),.
(3),,,.
【分析】(1)根据交事件(积事件)的概念求解即可;
(2)根据并事件(和事件)的概念求解即可;
(3)根据对立事件与交事件、并事件运算求解即可.
【详解】(1),,,
,.
(2),,,
,.
(3),,,,.
,,
,,,.
21.
【分析】结合独立事件公式直接计算即可.
【详解】设一次测试甲通过测试的事件为,由题可知,甲第三次,第四次一定没通过测试,则第二次一定通过测试,第一次通不通过测试不受影响,故甲恰好参加四次技能测试后被撤销上岗资格的概率.
22.(1);(2).
【分析】(1)根据表中数据知未参加志愿服务礼仪培训又未参加赛会应急救援培训的有30人,故至少参加上述一个培训的共有人.从而求得概率;
(2)从这5名男同学和3名女同学中各随机选1人,列出其一切可能的结果,从而求得被选中且未被选中的概率.
【详解】解:由调查数据可知,既未参加志愿服务礼仪培训又未参加赛会应急救援培训的有30人,
故至少参加上述一个培训的共有人.
从该班随机选1名同学,该同学至少参加上述一个培训的概率为;
从这5名男同学和3名女同学中各随机选1人,其一切可能的结果组成的基本事件有:
,
,
,
共15个,
根据题意,这些基本事件的出现是等可能的,
事件“被选中且未被选中”所包含的基本事件有:,共2个,
被选中且未被选中的概率为.
答案第1页,共2页
答案第1页,共2页
1.若随机事件,互斥,,发生的概率均不等于0,且,,则实数的取值范围是( )
A. B. C. D.
2.如图,“红旗-9”在国内外都被认为属于第三代防空导弹系统,其杀伤空域大,抗干扰和抗多目标饱和攻击能力强,导引系统先进(有两级指挥管制体制),最高速度4.2马赫,最大射程为200公里,射高0.5至30公里,主要攻击高空敌机或导弹,是我国高空防空导弹的杰出代表.现假设在一次实战对抗演习中,单发红旗-9防空导弹对敌方高速飞行器的拦截成功率为0.8,则两发齐射(是否成功拦截互不干扰),敌方高速飞行器被拦截的概率为( )
A.0.96 B.0.88 C.1.6 D.0.64
3.某中学的学生积极参加体育锻炼,其中有96%的学生喜欢足球或游泳,60%的学生喜欢足球,82%的学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是( )
A.62% B.56%
C.46% D.42%
4.抛掷两枚均匀的骰子,记录正面朝上的点数,则下列选项的两个事件中,互斥但不对立的是( )
A.事件“点数之和为奇数”与事件“点数之和为9”
B.事件“点数之和为偶数”与事件“点数之和为奇数”
C.事件“点数之和为6”与事件“点数之和为9”
D.事件“点数之和不小于9”与事件“点数之和小于等于8”
5.某大学进行“羽毛球”、“美术”、“音乐”三个社团选拔.某同学经过考核选拔通过该校的“羽毛球”“美术”、“音乐”三个社团的概率依次为,已知三个社团中他恰好能进入两个的概率为,假设该同学经过考核通过这三个社团选拔成功与否相互独立,则该同学一个社团都不能进入的概率为( )
A. B. C. D.
6.下列各对事件中,不互为相互独立事件的是( )
A.掷一枚骰子一次,事件“出现偶数点”;事件“出现3点或6点”
B.袋中有3白、2黑共5个大小相同的小球,依次有放回地摸两球,事件“第一次摸到白球”,事件“第二次摸到白球”
C.袋中有3白、2黑共5个大小相同的小球,依次不放回地摸两球,事件“第一次摸到白球”,事件“第二次摸到黑球”
D.甲组3名男生,2名女生;乙组2名男生,3名女生,现从甲、乙两组中各选1名同学参加演讲比赛,事件“从甲组中选出1名男生”,事件“从乙组中选出1名女生”
7.若连续抛掷两次质地均匀的骰子,得到的点数分别为m,n,则满足的概率是( )
A. B. C. D.
8.某学校共有教职工120人,对他们进行年龄结构和受教育程度的调查,其结果如下表:
本科 研究生 合计
35岁以下 40 30 70
35-50岁 27 13 40
50岁以上 8 2 10
现从该校教职工中任取1人,则下列结论正确的是( )A.该教职工具有本科学历的概率低于60%
B.该教职工具有研究生学历的概率超过50%
C.该教职工的年龄在50岁以上的概率超过10%
D.该教职工的年龄在35岁及以上且具有研究生学历的概率超过10%
二、多选题
9.下列有关古典概型的说法中,正确的是( )
A.试验的样本空间的样本点总数有限
B.每个事件出现的可能性相等
C.每个样本点出现的可能性相等
D.已知样本点总数为,若随机事件包含个样本点,则事件发生的概率
10.抛掷两枚质地均匀的骰子,记“第一枚骰子出现的点数小于3”为事件A,“第二枚骰子出现的点数不小于3”为事件B,则下列结论中正确的是( )
A.事件A与事件B互为对立事件
B.事件A与事件B相互独立
C.
D.
11.下列说法中正确的有( )
A.若事件A与事件B是互斥事件,则
B.若事件A与事件B是对立事件,则
C.某人打靶时连续射击三次,则事件“至少有两次中靶”与事件“至多有一次中靶”是对立事件
D.把红、橙、黄3张纸牌随机分给甲、乙、丙3人,每人分得1张,则事件“甲分得的不是红牌”与事件“乙分得的不是红牌”是互斥事件
12.下列说法错误的是( )
A.随着试验次数的增大,随机事件发生的频率会逐渐稳定于该随机事件发生的概率
B.某种福利彩票的中奖概率为,买1000张这种彩票一定能中奖
C.连续100次掷一枚硬币,结果出现了49次反面,则掷一枚硬币出现反面的概率为
D.某市气象台预报“明天本市降水概率为70%”,指的是:该市气象台专家中,有70%认为明天会降水,30%认为明天不会降水
三、填空题
13.甲、乙两人进行乒乓球比赛,比赛规则为“三局两胜制”(即先赢两局者为胜,若前两局某人连胜,则无需比第三局),根据以往两人的比赛数据分析,甲在每局比赛中获胜的概率为,则本次比赛中甲获胜的概率为___________.
14.已知小张每次射击命中十环的概率都为40%,现采用随机模拟的方法估计小张三次射击恰有两次命中十环的概率,先由计算器产生0到9之间取整数值的随机数,指定2,4,6,8表示命中十环,0,1,3,5,7,9表示未命中十环,再以每三个随机数为一组,代表三次射击的结果,经随机模拟产生了如下20组随机数:据此估计,小张三次射击恰有两次命中十环的概率约为__________.
15.连续掷一颗骰子两次,事件“向上的点数之和为”相对应的基本事件空间是____________________.
16.已知甲、乙两名篮球运动员投篮投中的概率分别为0.5和0.8,且甲、乙两人投篮的结果互不影响.若甲、乙两人各投篮一次,则至少有一人投中的概率为_____.
四、解答题
17.某种婴儿用品主要材质是橡胶,在加工过程中,可能会残留一些未挥发完全的溶剂,以及橡胶本身含有的化合物等,长期潜伏积累,对免疫力尚未健全的婴幼儿会危害甚大,为了测量此类新产品的挥发性物质含量,从生产的产品中随机抽取100个,得到如下频率分布直方图,若以频率作为概率,规定该婴儿用品的挥发性物质含量<18‰为合格产品.
(1)若这100个产品的挥发性物质含量的平均值大于16,则需进行技术改进,试问该新产品是否需要技术改进?
(2)为了解产品不合格的原因,用分层抽样的方法从与中抽取6个进行分析,然后从这6个中抽取2个进一步实验,求2个均在内的概率.
18.“2021年全国城市节约用水宣传周”已于5月9日至15日举行.成都市围绕“贯彻新发展理念,建设节水型城市”这一主题,开展了形式多样,内容丰富的活动,进一步增强全民保护水资源,防治水污染,节约用水的意识.为了解活动开展成效,某街道办事处工作人员赴一小区调查住户的节约用水情况,随机抽取了300名业主进行节约用水调查评分,将得到的分数分成6组:[70,75),[75,80),[80,85),[85,90),[90,95),[95,100],得到如图所示的频率分布直方图.
(1)求a的值,并估计这300名业主评分的中位数、平均数、众数;
(2)若先用分层抽样的方法从评分在[90,95)和[95,100]的业主中抽取5人,然后再从抽出的这5位业主中任意选取2人作进一步访谈,求这2人中至少有1人的评分在[95,100]概率.
19.书籍是精神世界的入口,阅读让精神世界闪光,阅读逐渐成为许多人的一种生活习惯,每年4月23日为世界读书日.某研究机构为了解某地年轻人的阅读情况,通过随机抽样调查了100位年轻人,对这些人每天的阅读时间(单位:分钟)进行统计,得到样本的频率分布直方图,如图所示.
(1)求;
(2)根据频率分布直方图,估计这100位年轻人每天阅读时间的平均数(单位:分钟);(同一组数据用该组数据区间的中点值表示)
(3)为了进一步了解年轻人的阅读方式,研究机构采用分层抽样的方法从每天阅读时间位于分组,和的年轻人中抽取5人,再从中任选2人进行调查,求其中至少有1人每天阅读时间位于的概率.
20.掷一个骰子,下列事件:,,,,.求:
(1), ;
(2),;
(3)记是事件的对立事件,求,,,.
21.某车间共有八名工人,为了保障安全生产,每月1号要从中选取四名工人参加同样的技能测试,每名工人通过每次测试的概率都是.甲从事的岗位比较特殊,每次他都必须参加技能测试.工厂规定:若工人连续两次没通过测试,则被撤销上岗资格.求甲恰好参加四次技能测试后被撤销上岗资格的概率.
22.在2016珠海航展志愿服务开始前,团珠海市委调查了北京师范大学珠海分校某班50名志愿者参加志愿服务礼仪培训和赛会应急救援培训的情况,数据如下表:单位:人
参加志愿服务礼仪培训 未参加志愿服务礼仪培训
参加赛会应急救援培训 8 8
未参加赛会应急救援培训 4 30
(1)从该班随机选1名同学,求该同学至少参加上述一个培训的概率;
(2)在既参加志愿服务礼仪培训又参加赛会应急救援培训的8名同学中,有5名男同学A,A,A,A,A名女同学B,B,B现从这5名男同学和3名女同学中各随机选1人,求A被选中且B未被选中的概率.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】利用互斥事件的加法公式及概率的基本性质列式即可作答.
【详解】因随机事件,互斥,则,
依题意及概率的性质得,即,解得,
所以实数的取值范围是.
故选:C
2.A
【分析】根据对立事件及相互独立事件的概率公式计算可得;
【详解】解:依题意敌方高速飞行器被拦截的概率为
故选:A
3.C
【分析】记“该中学学生喜欢足球”为事件,“该中学学生喜欢游泳”为事件,则“该中学学生喜欢足球或游泳”为事件,“该中学学生既喜欢足球又喜欢游泳”为事件,然后根据积事件的概率公式可得结果.
【详解】记“该中学学生喜欢足球”为事件,“该中学学生喜欢游泳”为事件,则“该中学学生喜欢足球或游泳”为事件,“该中学学生既喜欢足球又喜欢游泳”为事件,
则,,,
所以
所以该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例为.
故选:C.
【点睛】本题考查了积事件的概率公式,属于基础题.
4.C
【分析】利用对立事件、互斥事件的定义直接求解.
【详解】对于,二者能同时发生,不是互斥事件,故错误;
对于,二者不能同时发生,也不能同时不发生,是对立事件,故错误;
对于,二者不能同时发生,但能同时不发生,是互斥但不对立事件,故正确;
对于,二者不能同时发生,也不能同时不发生,是对立事件,故错误.
故选:.
5.D
【分析】根据互相独立事件的概率公式计算可得;
【详解】解:由题知,三个社团中他恰好能进入两个的概率为,则,所以,所以,所以该同学一个社团都不进入的概率.
故选:D.
6.C
【分析】利用对立事件和相互独立事件的概念求解.
【详解】解:对于选项A,事件,事件,事件,基本事件空间,所以,,,即,因此事件与事件N是相互独立事件;
对于选项B,袋中有3白、2黑共5个大小相同的小球,依次有放回地摸两球,事件“第一次摸到白球”,事件“第二次摸到白球”, 则事件发生与否与无关,同时,事件发生与否与无关,则事件与事件是相互独立事件;
对于选项C,袋中有3白、2黑,5个大小相同的小球,依次不放回地摸两球, 事件“第一次摸到白球”,事件“第二次摸到黑球”, 则事件发生与否和事件有关,故事件和事件与不是相互独立事件;
对于选项D,甲组3名男生,2名女生;乙组2名男生,3名女生,现从甲、乙两组中各选1名同学参加演讲比赛,事件“从甲组中选出1名男生”,事件“从乙组中选出1名女生”,则事件发生与否与无关,同时,事件发生与否与无关,则事件与事件是相互独立事件;
故选:C.
7.B
【分析】利用列举法列出所有可能结果,再根据古典概型的概率公式计算可得.
【详解】解:设连续投掷两次骰子,得到的点数依次为、,两次抛掷得到的结果可以用表示,
则结果有,,,,,,
,,,,,,
,,,,,,
,,,,,,
,,,,,,
,,,,,,
共有36种.
其中满足有:,,,,,,,,,,,,,共种,
所以满足的概率.
故选:B
8.D
【分析】根据表中数据,用频率代替概率求解.
【详解】A.该教职工具有本科学历的概率 ,故错误;
B.该教职工具有研究生学历的概率,故错误;
C.该教职工的年龄在50岁以上的概率,故错误;
D.该教职工的年龄在35岁及以上且具有研究生学历的概率,故正确.
【点睛】本题主要考查概率的求法,还考查了分析求解问题的能力,属于基础题.
9.ACD
【分析】根据古典概型的定义逐项判断即可.
【详解】由古典概型概念可知:试验的样本空间的样本点总数有限;每个样本点出现的可能性相等.
故AC正确;每个事件不一定是样本点,可能包含若干个样本点,所以B不正确;
根据古典概型的概率计算公式可知D正确.
故选:ACD
10.BCD
【分析】利用对立事件的意义判断A;利用相互独立事件的定义判断B;由事件A,B的概率计算判断C,D作答.
【详解】依题意,第一枚骰子出现的点数小于3与第二枚骰子出现的点数不小于3可以同时发生,
即事件A与事件B不互斥,则事件A与事件B不是对立事件,A不正确;
显然有,
抛掷两枚质地均匀的骰子的试验的所有结果:
,共36个,它们等可能,
事件AB所含的结果有:,共8个,
则有,即事件A与事件B相互独立,B正确;
显然,,C,D都正确.
故选:BCD
11.ABC
【分析】根据互斥事件、对立事件的概念判断即可.
【详解】解:事件与事件互斥,则不可能同时发生,所以,故A正确;
事件与事件是对立事件,则事件即为事件,所以,故B正确;
事件“至少两次中靶”与“至多一次中靶”不可能同时发生,且二者必发生其一,所以为对立事件,故C正确;
“甲分得的不是红牌”与事件“乙分得的不是红牌”可能同时发生,即“丙分得的是红牌”,所以不是互斥事件,故D错误.
故选:ABC
12.BCD
【分析】根据概率的定义和生活中的概率判断各选项的对错.
【详解】由频率和概率的关系可知随着试验次数的增大,随机事件发生的频率会逐渐稳定于该随机事件发生的概率,A正确,
某种福利彩票的中奖概率为,买1000张这种彩票不一定能中奖,B错误,
掷一枚硬币出现反面的概率为,C错误,
某市气象台预报“明天本市降水概率为70%”,指的是明天有70%的可能会降水,D错误,
故选:BCD.
13.
【分析】根据题意,利用相互独立事件的概率乘法公式分别求得甲前两局获胜的概率和前两局中一胜一负,第三局胜利的概率,结合互斥事件的概率加法公式,即可求解.
【详解】因为甲在每局比赛中获胜的概率为,
若甲前两局获胜,其概率为;
若甲前两局中一胜一负,第三局胜利,其概率为,
所以本次比赛中甲获胜的概率为.
故答案为:.
14.0.3
【分析】确定随机数组中以恰有两个数字是2,4,6,8,再由概率公式计算.
【详解】由题意,随机数组421,292,274,632,478,663共6个,表示恰有两次命中十环,
所以概率为.
故答案为:0.3.
15.
【分析】用列举法可得出两次点数之和为包含的基本事件.
【详解】将一颗骰子先后抛掷两次,观察向上的点数,
基本事件总数,
两次点数之和为包含的基本事件有:
故答案为:
16.0.9
【分析】根据对立事件的概率公式即可求出.
【详解】设“甲、乙两人各投篮一次,则至少有一人投中”,
则.
故答案为:0.9.
17.(1)该产品需要进行技术改进;(2).
【分析】(1)、由频率分布直方图求出平均值判断与16的大小关系即可得出结论;
(2)、先根据分层抽样求得在与中所抽取的个数,运用列举法列出事件的所有情况,由古典概率公式可求得答案.
【详解】(1)∵,故该产品需要进行技术改进;
(2)组的产品的个数为,组的产品的个数,所以从组中抽取个,从组中抽取个,
记组中抽取的5个分别为,组中抽取的一个为,
则从6个中抽取2个的所有情况如下:共15种情况,
其中在中恰有2个的有共10种情况,所以所求的概率.
18.(1),中位数为85,平均数为84.625,众数为87.5
(2)
【分析】(1)由频率分布直方图的的性质,所有小矩形的面积之和为1,可解得的值,由中位数的定义,找到频率之和为的点,平均数的估计值公式为每个小矩形的中点值与对应小矩形面积的乘积之和,众数估计值为最高小矩形的中点;
(2)首先根据两个分组的人数之比,采用分层抽样的方法,得到每个分组抽取的人数,则采用列举法,罗列多有情况和符合题意的情况,根据古典概型的概率计算公式得到答案.
(1)
∵第三组的频率为1-(0.020+0.025+0.030+0.035+0.050)×5=0.200,
又第一组的频率为0.025×5=0.125,第二组的频率为0.035×5=0.175,
第三组的频率为0.200.∵前三组的频率之和为0.125+0.175+0.200=0.500,
∴这300名业主评分的中位数为85.
平均数为72.5×0.025×5+77.5×0.035×5+82.5×0.040×5+87.5×0.050×5+92.5×0.030×5+97.5×0.020×5=84.625.
众数为(85+90)÷2=87.5.
(2)
由频率分布直方图,知评分在[90,95)的人数与评分在[95,100]的人数的比值为3:2.
∴采用分层抽样法抽取5人,评分在[90,95)的有3人,评分在[95,100]有2人.
不妨设评分在[90,95)的3人分别为;评分在[95,100]的2人分别为.
则从5人中任选2人的所有可能情况有:
{A1,A2},{A1,A3},{A1,B1},{A1,B2},{A2,A3},{A2,B1},{A2,B2},{A3,B1},{A3,B2},{B1,B2},共10种.
其中选取的2人中至少有1人的评分在[95,100]的情况有:
{A1,B1},{A1,B2},{A2,B1},{A2,B2},{A3,B1},{A3,B2},{B1,B2},共7种.
故这2人中至少有1人的评分在[95,100]的概率为.
19.(1);(2)74;(3).
【分析】(1)利用小矩形的面积之和等于即可求解.
(2)根据频率分布直方图,由小矩形底边中点横坐标与小矩形面积乘积之和即可求解.
(3)根据频率分布直方图得出频率比,从中任选2人列出基本事件个数,根据古典概型的概率计算公式即可求解.
【详解】解:(1)根据频率分布直方图得:
(2)根据频率分布直方图得:
,
(3)由于,和的频率之比为:1∶2∶2,
故抽取的5人中,和分别为:1人,2人,2人,
记的1人为,的2人为,,的2人为,
故随机抽取2人共有,,,,,,
,,,10种,
其中至少有1人每天阅读时间位于的包含7种,
故概率.
20.(1),.
(2),.
(3),,,.
【分析】(1)根据交事件(积事件)的概念求解即可;
(2)根据并事件(和事件)的概念求解即可;
(3)根据对立事件与交事件、并事件运算求解即可.
【详解】(1),,,
,.
(2),,,
,.
(3),,,,.
,,
,,,.
21.
【分析】结合独立事件公式直接计算即可.
【详解】设一次测试甲通过测试的事件为,由题可知,甲第三次,第四次一定没通过测试,则第二次一定通过测试,第一次通不通过测试不受影响,故甲恰好参加四次技能测试后被撤销上岗资格的概率.
22.(1);(2).
【分析】(1)根据表中数据知未参加志愿服务礼仪培训又未参加赛会应急救援培训的有30人,故至少参加上述一个培训的共有人.从而求得概率;
(2)从这5名男同学和3名女同学中各随机选1人,列出其一切可能的结果,从而求得被选中且未被选中的概率.
【详解】解:由调查数据可知,既未参加志愿服务礼仪培训又未参加赛会应急救援培训的有30人,
故至少参加上述一个培训的共有人.
从该班随机选1名同学,该同学至少参加上述一个培训的概率为;
从这5名男同学和3名女同学中各随机选1人,其一切可能的结果组成的基本事件有:
,
,
,
共15个,
根据题意,这些基本事件的出现是等可能的,
事件“被选中且未被选中”所包含的基本事件有:,共2个,
被选中且未被选中的概率为.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
