【新课标】1.2二次函数的图象与性质(1) 课件(共32张PPT)
文档属性
| 名称 | 【新课标】1.2二次函数的图象与性质(1) 课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-20 15:00:11 | ||
图片预览









文档简介
(共32张PPT)
1.2二次函数的图象与性质(1)
湘教版 九年级下
教学内容分析
掌握了二次函数的概念,熟悉二次函数的一般形式及自变量的取值范围,在此基础上,进一步认识二次函数y=ax2(a>0)图象的作图步骤,以及二次函数y=ax2(a>0)的性质。
教学目标
1.掌握二次函数y=ax2(a>0)图象的作图步骤;(重点)
2.通过画图,了解二次函数y=ax2的图象是一条曲线;
3.初步了解二次函数y=ax2(a>0)的性质(难点)
4.培养画图能力,增强合作意识,培养认真谨慎的习惯.
核心素养分析
熟悉二次函数的概念,让学生会画二次函数y=ax2(a>0)图象,学习和掌握二次函数y=ax2(a>0)的性质,锻炼学生动手操作能力,解决实际问题的能力。
新知导入
二次函数的一般形式是什么?二次项系数,一次项系数,常数项系数分别是什么?
一般形式是y=ax2+bx +c (a, b,c是常数,a≠0).
二次项系数,一次项系数,常数项系数分别是a, b,c
新知讲解
我们已经学习过用描点法画一次函数、反比例函数的图象, 如何画一个二次函数的图象呢?
新知讲解
画二次函数y=x2的图象.
探究
新知讲解
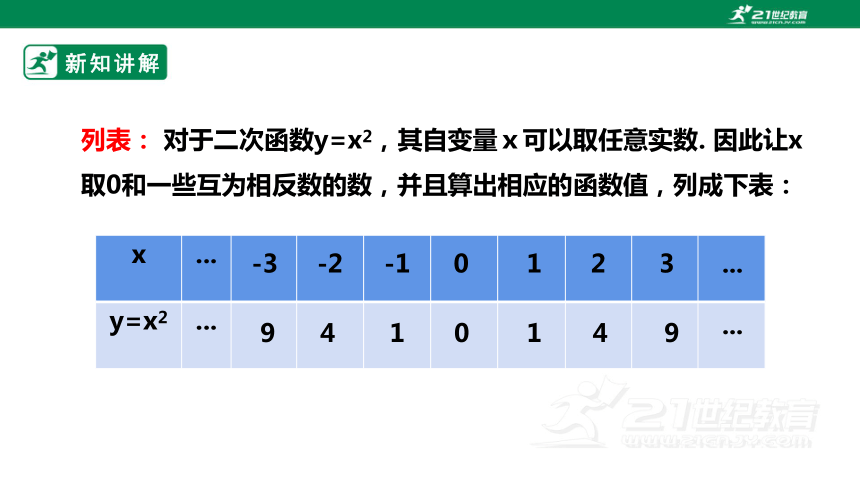
x ...
y=x2 ...
列表: 对于二次函数y=x2,其自变量x可以取任意实数. 因此让x取0和一些互为相反数的数,并且算出相应的函数值,列成下表:
-3
9
-2
4
-1
1
0
0
1
1
2
4
3
9
...
...
新知讲解
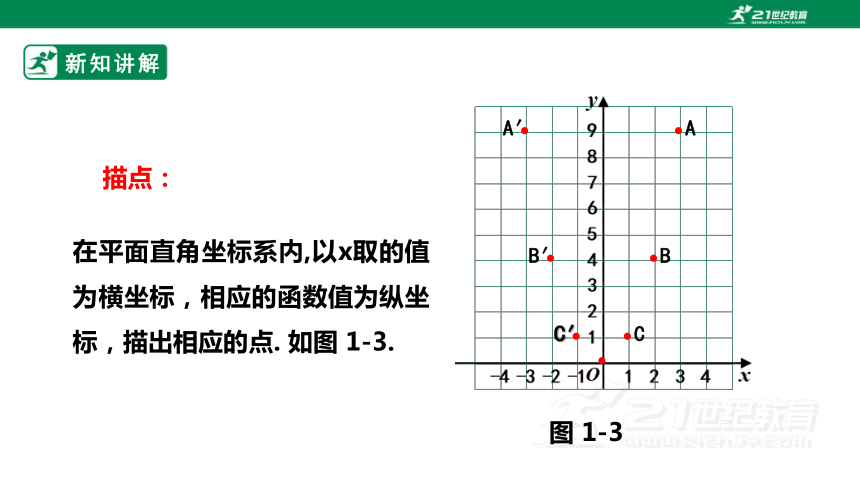
描点:
A
A′
B
B′
C
C′
图 1-3
在平面直角坐标系内,以x取的值为横坐标,相应的函数值为纵坐标,描出相应的点. 如图 1-3.
新知讲解
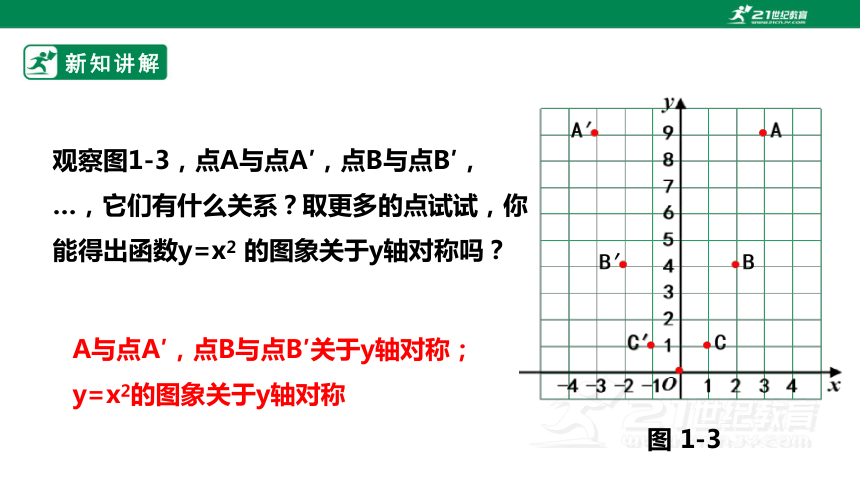
观察图1-3,点A与点A′,点B与点B′,
…,它们有什么关系?取更多的点试试,你能得出函数y=x2 的图象关于y轴对称吗?
A与点A′,点B与点B′关于y轴对称;y=x2的图象关于y轴对称
图 1-3
新知讲解
观察图1-3,
(1)y轴右边描出的各点,当横坐标增大时,纵坐标有什么变化
(2)y轴右边的所有点都具有纵坐标随着横坐标的增大而增大的特点吗
y轴右边的所有点都具有纵坐标随着横坐标的增大而增大的特点。
图 1-3
y轴右边描出的各点,当横坐标增大时,纵坐标增大;
新知讲解
y=x2的图象关于y轴对称;
图象在y轴右边的部分,函数值随自变量取值的增大而增大,简称为“右升”。
新知讲解
用一条光滑曲线把原点和y轴右边各点顺次连接起来;
然后利用对称性,画出图象在y轴左边的部分(把y轴左边的点和原点用一条光滑曲线顺次连接起来).
这样就得到了y=x2的图象,如图1-4.
图1-4
A
A′
B
B′
C
C′
连线:
注意:
(1)“连线”中“顺次”是指按自变量从小到大(或从大到小)的顺序,换句话说,就是从左到右(或从右到左)的顺序。
(2)描点法所画的图象只是整个图象的一部分,是近似的.
(3)在画图象时,一般来说,选点越多,图象越精确,但也要具体问题具体分析.
新知讲解
新知讲解
观察图1-4,函数y=x2的图象除了具有关于y轴对称和“右升”外,还具有哪些性质?
观察
图1-4
A
A′
B
B′
C
C′
新知讲解
二次函数y=x2的图象是一条曲线,它的开口向上,对称轴与图象的交点是原点(0,0);
图象在对称轴左边的部分, 函数值随自变量取值的增大而减小, 简称为“左降”;
当x=0时,函数值最小,最小值为 0.
新知讲解
画y=ax2(a>0)的图象时:
1、可以先画出图象在y轴右边的部分;
2、然后利用对称性,画出图象在y轴左边的部分;
3、在画右边部分时,只需”列表、描点、连线“三个步骤。
新知讲解
例 画二次函数 的图象
新知讲解
解 因为二次函数 的图象关于 y 轴对称,
因此列表时,自变量x可以从原点的横坐标0开始取值.
列表
x
0
1
2
3
...
0
2
...
新知讲解
描点和连线:
图1-5
(1)
A
B
C
画出图象在y轴右边的部分. 如图1-5(1).
(2)
新知讲解
利用对称性,画出图象在y轴左边的对称点,
并用一条光滑曲线把y 轴左边的点和原点顺次连接起来,这样就得到了的图象. 如图1-5(2).
图1-5
A
B
C
A′
B′
C′
新知讲解
y=x2
比较y=x2与 的开口程度,对于抛物线y=ax2,|a|的大小与抛物线的开口关系?
|a|的大小决定抛物线的开口程度,|a|相等说明抛物线的开口大小相同,即抛物线的形状相同;
|a|越大,抛物线的开口越小;
|a|越小,抛物线的开口越大;
课堂练习
1、关于函数y=3x2的性质表述正确的一项是 ( )
A. 无论x为任何实数,y的值总为正
B. 当x值增大时,y的值也增大
C. 它的图象关于y轴对称
D. 它的图象在第一、三象限内
C
课堂练习
解:
A、当x=0时,y=0,故此选项错误;
B、当x>0时,y随x的增大而增大;当x<0时,y随x的增大而减小,故此选项错误;
C、二次函数y=x2的图象开口向上,对称轴为y轴,此选项正确;
D、它的图象在第一、二象限内,故此选项错误.
课堂练习
2、画出二次函数y=6x2的图象,并填空:
(1)图象的对称轴是______,对称轴与图象的交点是______;
(2)图象的开口向______;
(3)图象在对称轴左边的部分,函数值随自变量取值的增大而______;图象在对称轴右边的部分,函数值随自变量取值的增大而______.
课堂练习
解:(1)由图象可得,图象的对称轴是直线x=0,对称轴与图象的交点(0,0),
(2)图象的开口向上,
(3)图象在对称轴左边的部分,函数值随自变量取值的增大而减小;图象在对称轴右边的部分,函数值随自变量取值的增大而增大.
课堂练习
3、已知抛物线y=ax2与y=4x2的形状相同,则a的值是 ( )
A. 4 B. -4 C. ±4 D. 1
C
解:对于抛物线y=ax2,|a|的大小决定抛物线的开口程度,|a|相等说明抛物线的开口大小相同,即抛物线的形状相同,
∴a=±4,
课堂总结
二次函数的
图象与性质
2.二次函数y=ax2(a>0)图象的性质:
开口向上的一条曲线,
关于y轴对称,
对称轴与图象的交点是原点(0,0),左降,右升
1. 画二次函数y=ax2图象的三步骤:
列表、描点、连线
板书设计
1.2二次函数的图象与性质
1.画二次函数的步骤:列表、描点、连线
2.二次函数y=ax2(a>0)的图象与性质
作业布置
必做题:课本第7页练习 的第1,2题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.2二次函数的图象与性质(1)
湘教版 九年级下
教学内容分析
掌握了二次函数的概念,熟悉二次函数的一般形式及自变量的取值范围,在此基础上,进一步认识二次函数y=ax2(a>0)图象的作图步骤,以及二次函数y=ax2(a>0)的性质。
教学目标
1.掌握二次函数y=ax2(a>0)图象的作图步骤;(重点)
2.通过画图,了解二次函数y=ax2的图象是一条曲线;
3.初步了解二次函数y=ax2(a>0)的性质(难点)
4.培养画图能力,增强合作意识,培养认真谨慎的习惯.
核心素养分析
熟悉二次函数的概念,让学生会画二次函数y=ax2(a>0)图象,学习和掌握二次函数y=ax2(a>0)的性质,锻炼学生动手操作能力,解决实际问题的能力。
新知导入
二次函数的一般形式是什么?二次项系数,一次项系数,常数项系数分别是什么?
一般形式是y=ax2+bx +c (a, b,c是常数,a≠0).
二次项系数,一次项系数,常数项系数分别是a, b,c
新知讲解
我们已经学习过用描点法画一次函数、反比例函数的图象, 如何画一个二次函数的图象呢?
新知讲解
画二次函数y=x2的图象.
探究
新知讲解
x ...
y=x2 ...
列表: 对于二次函数y=x2,其自变量x可以取任意实数. 因此让x取0和一些互为相反数的数,并且算出相应的函数值,列成下表:
-3
9
-2
4
-1
1
0
0
1
1
2
4
3
9
...
...
新知讲解
描点:
A
A′
B
B′
C
C′
图 1-3
在平面直角坐标系内,以x取的值为横坐标,相应的函数值为纵坐标,描出相应的点. 如图 1-3.
新知讲解
观察图1-3,点A与点A′,点B与点B′,
…,它们有什么关系?取更多的点试试,你能得出函数y=x2 的图象关于y轴对称吗?
A与点A′,点B与点B′关于y轴对称;y=x2的图象关于y轴对称
图 1-3
新知讲解
观察图1-3,
(1)y轴右边描出的各点,当横坐标增大时,纵坐标有什么变化
(2)y轴右边的所有点都具有纵坐标随着横坐标的增大而增大的特点吗
y轴右边的所有点都具有纵坐标随着横坐标的增大而增大的特点。
图 1-3
y轴右边描出的各点,当横坐标增大时,纵坐标增大;
新知讲解
y=x2的图象关于y轴对称;
图象在y轴右边的部分,函数值随自变量取值的增大而增大,简称为“右升”。
新知讲解
用一条光滑曲线把原点和y轴右边各点顺次连接起来;
然后利用对称性,画出图象在y轴左边的部分(把y轴左边的点和原点用一条光滑曲线顺次连接起来).
这样就得到了y=x2的图象,如图1-4.
图1-4
A
A′
B
B′
C
C′
连线:
注意:
(1)“连线”中“顺次”是指按自变量从小到大(或从大到小)的顺序,换句话说,就是从左到右(或从右到左)的顺序。
(2)描点法所画的图象只是整个图象的一部分,是近似的.
(3)在画图象时,一般来说,选点越多,图象越精确,但也要具体问题具体分析.
新知讲解
新知讲解
观察图1-4,函数y=x2的图象除了具有关于y轴对称和“右升”外,还具有哪些性质?
观察
图1-4
A
A′
B
B′
C
C′
新知讲解
二次函数y=x2的图象是一条曲线,它的开口向上,对称轴与图象的交点是原点(0,0);
图象在对称轴左边的部分, 函数值随自变量取值的增大而减小, 简称为“左降”;
当x=0时,函数值最小,最小值为 0.
新知讲解
画y=ax2(a>0)的图象时:
1、可以先画出图象在y轴右边的部分;
2、然后利用对称性,画出图象在y轴左边的部分;
3、在画右边部分时,只需”列表、描点、连线“三个步骤。
新知讲解
例 画二次函数 的图象
新知讲解
解 因为二次函数 的图象关于 y 轴对称,
因此列表时,自变量x可以从原点的横坐标0开始取值.
列表
x
0
1
2
3
...
0
2
...
新知讲解
描点和连线:
图1-5
(1)
A
B
C
画出图象在y轴右边的部分. 如图1-5(1).
(2)
新知讲解
利用对称性,画出图象在y轴左边的对称点,
并用一条光滑曲线把y 轴左边的点和原点顺次连接起来,这样就得到了的图象. 如图1-5(2).
图1-5
A
B
C
A′
B′
C′
新知讲解
y=x2
比较y=x2与 的开口程度,对于抛物线y=ax2,|a|的大小与抛物线的开口关系?
|a|的大小决定抛物线的开口程度,|a|相等说明抛物线的开口大小相同,即抛物线的形状相同;
|a|越大,抛物线的开口越小;
|a|越小,抛物线的开口越大;
课堂练习
1、关于函数y=3x2的性质表述正确的一项是 ( )
A. 无论x为任何实数,y的值总为正
B. 当x值增大时,y的值也增大
C. 它的图象关于y轴对称
D. 它的图象在第一、三象限内
C
课堂练习
解:
A、当x=0时,y=0,故此选项错误;
B、当x>0时,y随x的增大而增大;当x<0时,y随x的增大而减小,故此选项错误;
C、二次函数y=x2的图象开口向上,对称轴为y轴,此选项正确;
D、它的图象在第一、二象限内,故此选项错误.
课堂练习
2、画出二次函数y=6x2的图象,并填空:
(1)图象的对称轴是______,对称轴与图象的交点是______;
(2)图象的开口向______;
(3)图象在对称轴左边的部分,函数值随自变量取值的增大而______;图象在对称轴右边的部分,函数值随自变量取值的增大而______.
课堂练习
解:(1)由图象可得,图象的对称轴是直线x=0,对称轴与图象的交点(0,0),
(2)图象的开口向上,
(3)图象在对称轴左边的部分,函数值随自变量取值的增大而减小;图象在对称轴右边的部分,函数值随自变量取值的增大而增大.
课堂练习
3、已知抛物线y=ax2与y=4x2的形状相同,则a的值是 ( )
A. 4 B. -4 C. ±4 D. 1
C
解:对于抛物线y=ax2,|a|的大小决定抛物线的开口程度,|a|相等说明抛物线的开口大小相同,即抛物线的形状相同,
∴a=±4,
课堂总结
二次函数的
图象与性质
2.二次函数y=ax2(a>0)图象的性质:
开口向上的一条曲线,
关于y轴对称,
对称轴与图象的交点是原点(0,0),左降,右升
1. 画二次函数y=ax2图象的三步骤:
列表、描点、连线
板书设计
1.2二次函数的图象与性质
1.画二次函数的步骤:列表、描点、连线
2.二次函数y=ax2(a>0)的图象与性质
作业布置
必做题:课本第7页练习 的第1,2题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
