勾股定理的应用3[下学期]
图片预览


文档简介
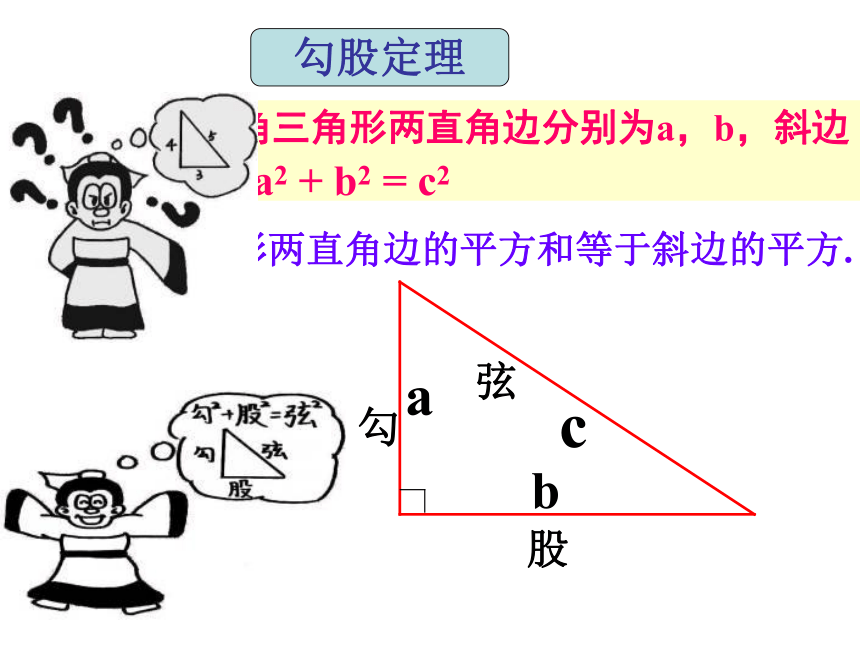
课件26张PPT。勾股定理3 如果直角三角形两直角边分别为a,b,斜边为c,那么a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方.勾股定理勾股弦(一)、填空题1、在Rt△ABC中,∠C=90°,
①若a=5,b=12,则c=______;
②若a=15,c=25,则b=_____;
③若c=61,b=60,则a=_____;
④若a∶b=3∶4,c=10则SRt△ABC=_____。 2.直角三角形两直角边长分别为5和12,则它斜边上的高为 13201124
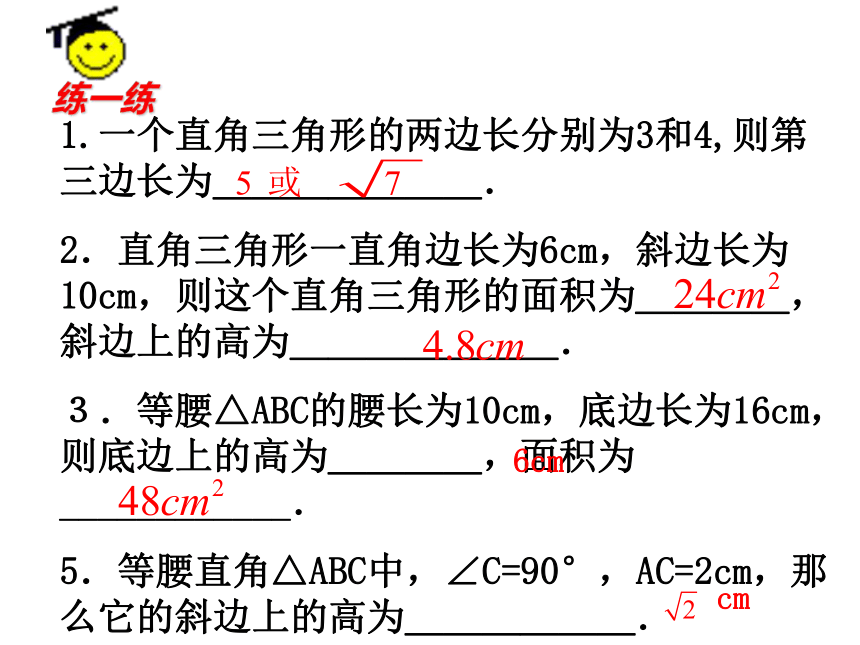
1.一个直角三角形的两边长分别为3和4,则第三边长为_______.
2.直角三角形一直角边长为6cm,斜边长为10cm,则这个直角三角形的面积为____,斜边上的高为_______.
3.等腰△ABC的腰长为10cm,底边长为16cm,则底边上的高为____,面积为____________.
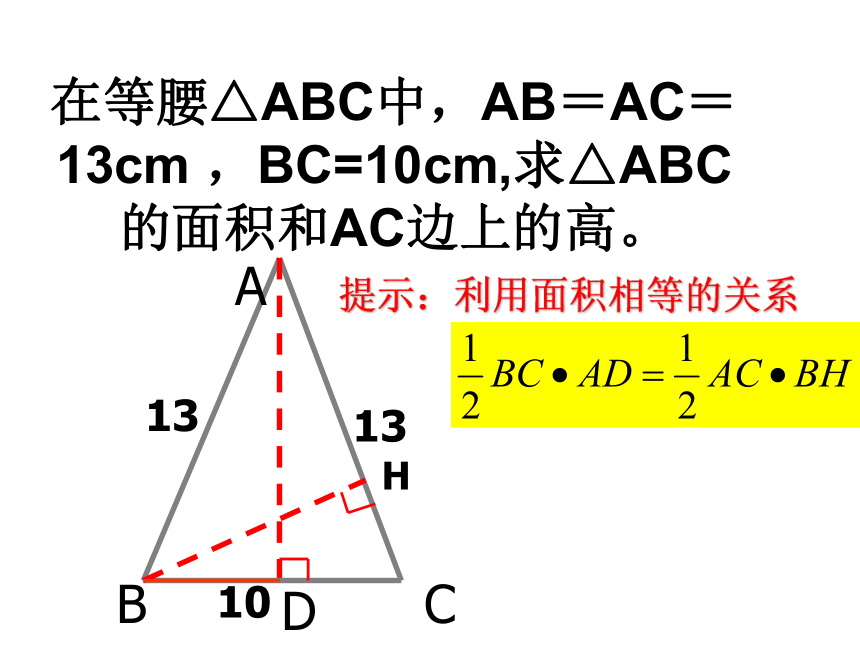
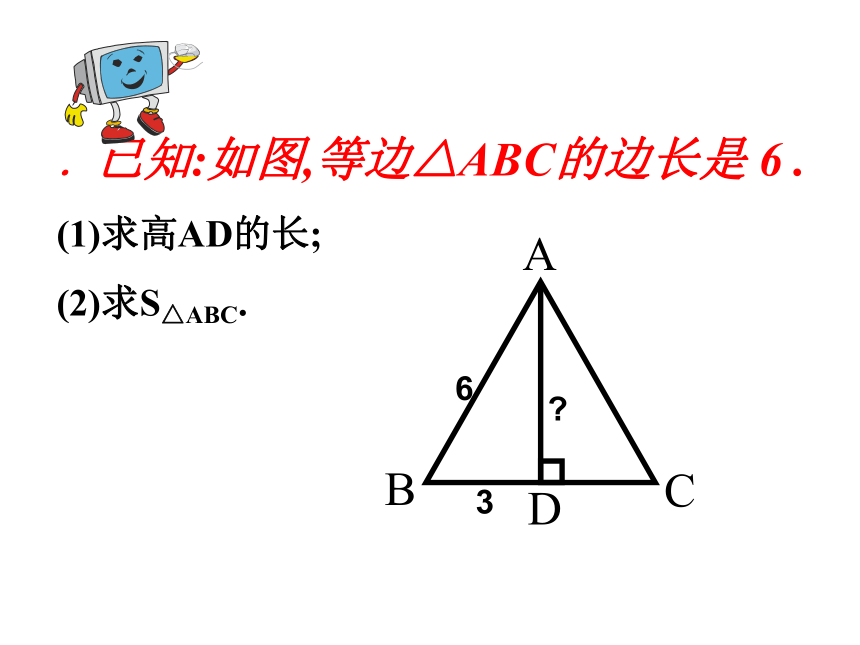
5.等腰直角△ABC中,∠C=90°,AC=2cm,那么它的斜边上的高为______.6cmcm 练一练在等腰△ABC中,AB=AC=13cm ,BC=10cm,求△ABC的面积和AC边上的高。ABCD131310H提示:利用面积相等的关系 .已知:如图,等边△ABC的边长是 6 .
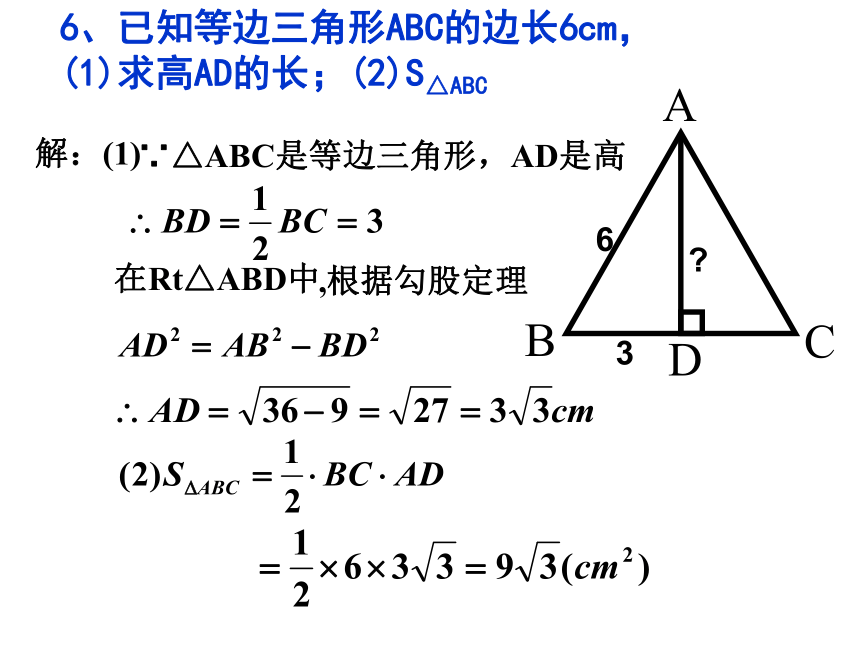
(1)求高AD的长;
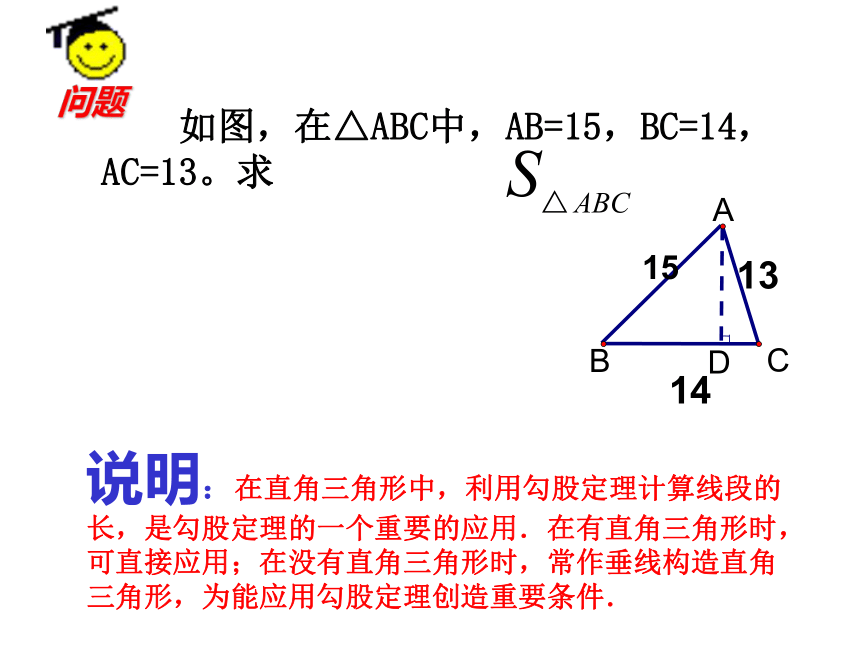
(2)求S△ABC.6、已知等边三角形ABC的边长6cm, (1)求高AD的长;(2)S△ABC解:(1)∵△ABC是等边三角形,AD是高在Rt△ABD中,根据勾股定理 如图,在△ABC中,AB=15,BC=14,AC=13。求DABC说明:在直角三角形中,利用勾股定理计算线段的长,是勾股定理的一个重要的应用.在有直角三角形时,可直接应用;在没有直角三角形时,常作垂线构造直角三角形,为能应用勾股定理创造重要条件. 问题1513141046810xEFDCBA8-x8-x 思维拓展: 有没有一种直角三角形,已知一边可以求另外两边长呢?在Rt△ABC中,∠C=90°(1)若∠A=300,a=6,则b= (2)若∠B=45,c=12,则a=(3)若∠B=60,c=8则00.如图,小方格都是边长为1的正方形,
求四边形ABCD的面积与周长.
如图,小方格都是边长为1的正方形,
求四边形ABCD的面积与周长.
EFGH实数数轴上的点一一对应说出下列数轴上各字母所表示的实数:点C表示 点D表示点B表示点A表示 我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上表示出 的点吗?01234步骤:lABC1、在数轴上找到点A,使OA=3;2、作直线l⊥OA,在l上取一点B,使AB=2;3,以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示 的点。探究3:数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?你能在数轴上画出表示 的点和 的点吗?∴点C即为表示 的点数学海螺图:利用勾股定理作出长为
的线段.11圆柱(锥)中的最值问题例 有一圆柱,底面圆的半径为3cm,高为12cm,一只蟑螂从底面的A处爬行到对角B处
吃偷食物,它爬行的最短路线长为多少?AB一只老鼠从距底面1cm的A处爬行到对角B处
偷吃食物,它爬行的最短路线长为多少?AB 例 如图是一个正方体土块,在正方体下底部的A点有一只蚂蚁,它想吃到上底面B点的食物(BC=3cm),需爬行的最短路程是多少?BACDC如果可以钻洞的话,最短路程是多少?例、如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?BA531512台阶中的最值问题∵ AB2=AC2+BC2=169,
∴ AB=13.再见
①若a=5,b=12,则c=______;
②若a=15,c=25,则b=_____;
③若c=61,b=60,则a=_____;
④若a∶b=3∶4,c=10则SRt△ABC=_____。 2.直角三角形两直角边长分别为5和12,则它斜边上的高为 13201124
1.一个直角三角形的两边长分别为3和4,则第三边长为_______.
2.直角三角形一直角边长为6cm,斜边长为10cm,则这个直角三角形的面积为____,斜边上的高为_______.
3.等腰△ABC的腰长为10cm,底边长为16cm,则底边上的高为____,面积为____________.
5.等腰直角△ABC中,∠C=90°,AC=2cm,那么它的斜边上的高为______.6cmcm 练一练在等腰△ABC中,AB=AC=13cm ,BC=10cm,求△ABC的面积和AC边上的高。ABCD131310H提示:利用面积相等的关系 .已知:如图,等边△ABC的边长是 6 .
(1)求高AD的长;
(2)求S△ABC.6、已知等边三角形ABC的边长6cm, (1)求高AD的长;(2)S△ABC解:(1)∵△ABC是等边三角形,AD是高在Rt△ABD中,根据勾股定理 如图,在△ABC中,AB=15,BC=14,AC=13。求DABC说明:在直角三角形中,利用勾股定理计算线段的长,是勾股定理的一个重要的应用.在有直角三角形时,可直接应用;在没有直角三角形时,常作垂线构造直角三角形,为能应用勾股定理创造重要条件. 问题1513141046810xEFDCBA8-x8-x 思维拓展: 有没有一种直角三角形,已知一边可以求另外两边长呢?在Rt△ABC中,∠C=90°(1)若∠A=300,a=6,则b= (2)若∠B=45,c=12,则a=(3)若∠B=60,c=8则00.如图,小方格都是边长为1的正方形,
求四边形ABCD的面积与周长.
如图,小方格都是边长为1的正方形,
求四边形ABCD的面积与周长.
EFGH实数数轴上的点一一对应说出下列数轴上各字母所表示的实数:点C表示 点D表示点B表示点A表示 我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上表示出 的点吗?01234步骤:lABC1、在数轴上找到点A,使OA=3;2、作直线l⊥OA,在l上取一点B,使AB=2;3,以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示 的点。探究3:数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?你能在数轴上画出表示 的点和 的点吗?∴点C即为表示 的点数学海螺图:利用勾股定理作出长为
的线段.11圆柱(锥)中的最值问题例 有一圆柱,底面圆的半径为3cm,高为12cm,一只蟑螂从底面的A处爬行到对角B处
吃偷食物,它爬行的最短路线长为多少?AB一只老鼠从距底面1cm的A处爬行到对角B处
偷吃食物,它爬行的最短路线长为多少?AB 例 如图是一个正方体土块,在正方体下底部的A点有一只蚂蚁,它想吃到上底面B点的食物(BC=3cm),需爬行的最短路程是多少?BACDC如果可以钻洞的话,最短路程是多少?例、如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?BA531512台阶中的最值问题∵ AB2=AC2+BC2=169,
∴ AB=13.再见
