勾股定理的应用[下学期]
文档属性
| 名称 | 勾股定理的应用[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 501.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-15 15:16:00 | ||
图片预览



文档简介
课件22张PPT。勾股定理的应用5
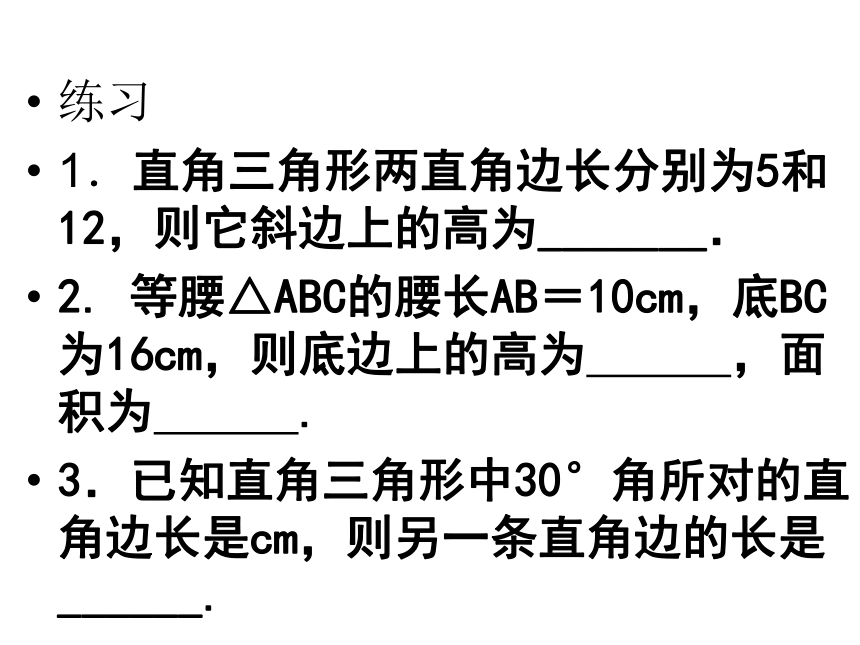
练习
1.直角三角形两直角边长分别为5和 12,则它斜边上的高为_______.
2. 等腰△ABC的腰长AB=10cm,底BC为16cm,则底边上的高为 ,面积为 .
3.已知直角三角形中30°角所对的直角边长是cm,则另一条直角边的长是 ______.4。如图,在高2米,坡角为30°的楼梯表面铺地毯,地毯的长度至少需要_____米.
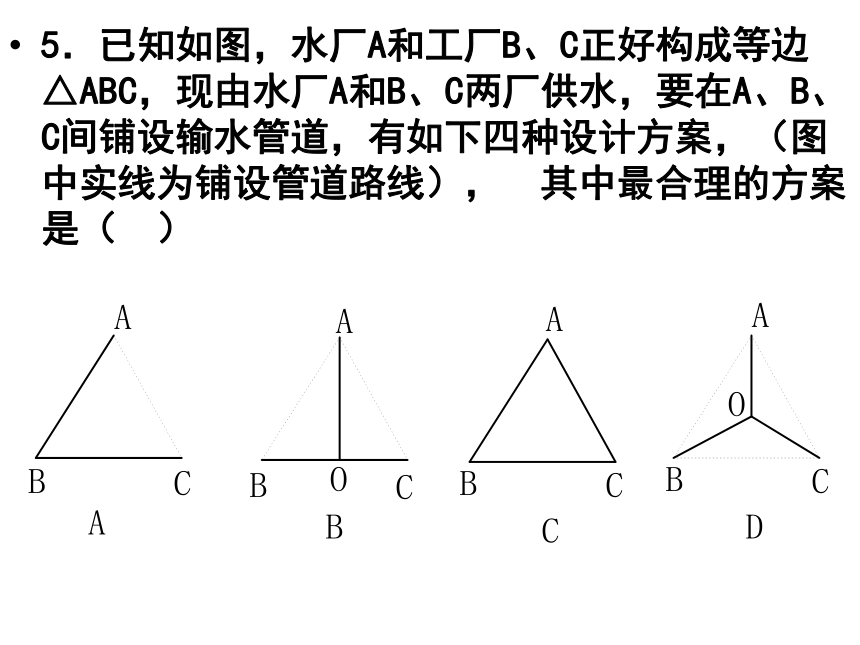
5.已知如图,水厂A和工厂B、C正好构成等边△ABC,现由水厂A和B、C两厂供水,要在A、B、C间铺设输水管道,有如下四种设计方案,(图中实线为铺设管道路线),其中最合理的方案是( )
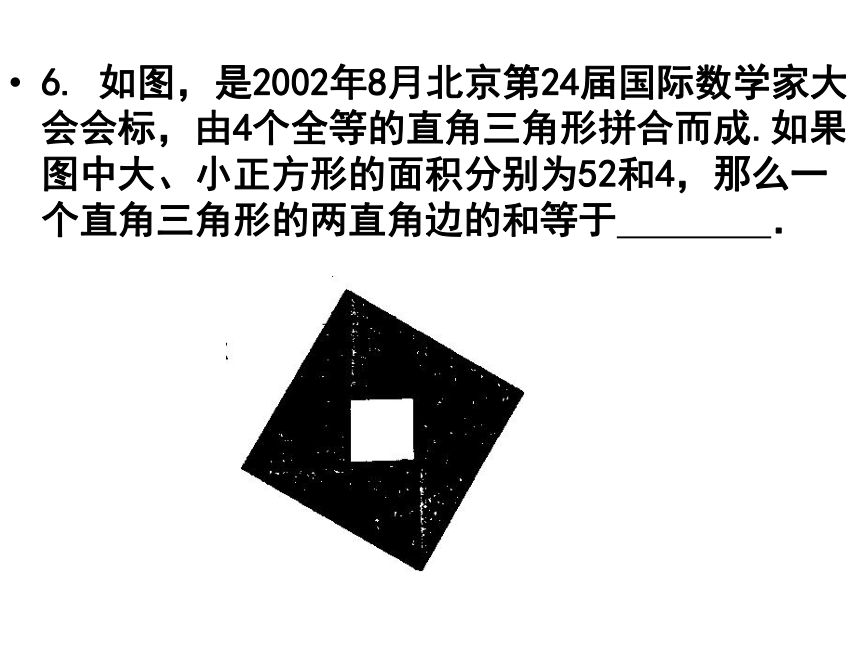
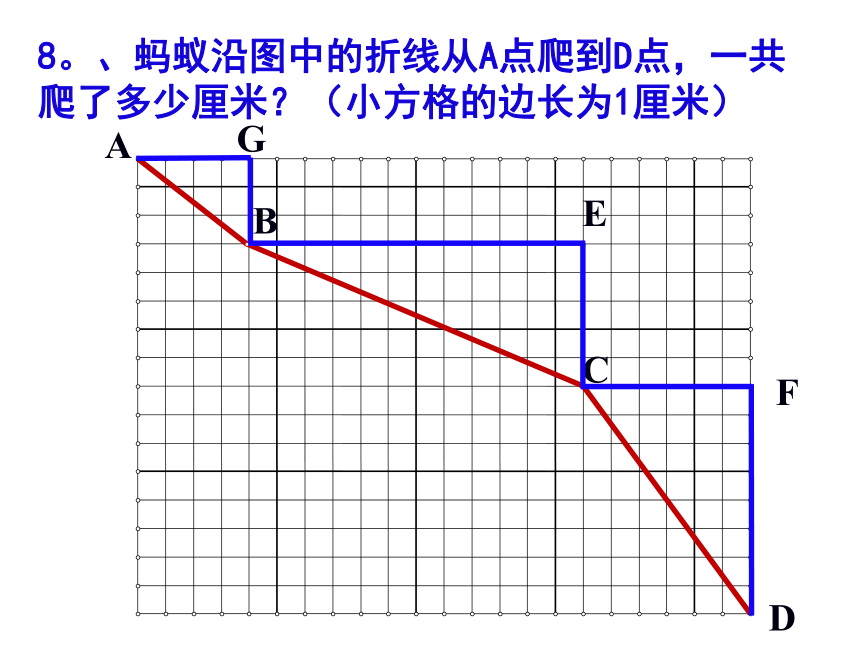
6. 如图,是2002年8月北京第24届国际数学家大会会标,由4个全等的直角三角形拼合而成.如果图中大、小正方形的面积分别为52和4,那么一个直角三角形的两直角边的和等于 .7.小刚准备测量河水的深度,他把一根竹竿插到离岸边1.5m远的水底,竹竿高出水面0.5m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,河水的深度为 .DA8。、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE圆柱(锥)中的最值问题例1。 有一圆柱,底面圆的半径为3cm,高为12cm,一只蟑螂从底面的A处爬行到对角B处
偷吃食物,它爬行的最短路线长为多少?AB一只老鼠从距底面1cm的A处爬行到对角B处
偷吃食物,它爬行的最短路线长为多少?AB 例2。 如图是一个正方体土块,在正方体下底部的A点有一只蚂蚁,它想吃到上底面B点的食物(BC=3cm),需爬行的最短路程是多少?BACDC如果可以钻洞的话,最短路程是多少? 如果盒子换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面需要爬行的最短路程又是多少呢? 变式分析:蚂蚁由A爬到B过程中较短的路线有多少种情况?(1)经过前面和上底面(2)经过前面和右面(3)经过下底面和右面 (1)当蚂蚁经过前面和上底面时,如图,最短路程为
AB= = =
(3)当蚂蚁经过下底面和右面时,如图,最短路程为
AB= = =
(2)当蚂蚁经过前面和右面时,如图,最短路程为
AB= =
=解:例3、如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?BA531512台阶中的最值问题∵ AB2=AC2+BC2=169,
∴ AB=13.练习1。在Rt△ABC中, ∠C=900,CD⊥AB于D, ∠A=600,CD= ,
求线段ABABCD2。在△ABC中,∠B=450,∠A=600,AC= 4
求线段ABABCD3。在四边形ABCD中, ∠A=600 , ∠B=∠D=900,AB= 4 ,CD=2
求:四边形ABCD的面积ABCDE 4。直角三角形的周长为30,斜边长为13,那么这个三角形的面积 为( )
A 15 B 30 C 60 D不能确定B 选一选5。已知,一轮船甲以16海里/时的速度从港口O出发向西北方向航行,另一轮船乙以12海里/时的速度同时从港口O出发向西南方向航行,离开港口2小时后,则两船相距( )
A、25海里 B、30海里 C、35海里 D、40海里
6。.台风是一种自然灾害,它以台风中心为圆心,在周围数十千米范围内形成气旋风暴,有极强的破坏力,据气象观测,距沿海某城市A的正南方向240km的B处有一台风中心,其中心风力为12级,每远离台风中心25km,风力就会减弱一级,该台风中心现正以20km/h的速度沿北偏东30°方向往C移动,如图所示,且台风中心的风力不变,若城市所受风力达到或超标四级,则称受台风影响.
(1)该城市是否受到台风影响?请说明理由;
(2)若会受到台风影响;那么台风影响该城市的持续时间有多长?
(3)该城市受到台风影响的最大风力为几级?7。如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?AB议一议 观察右图,用数格子的方法判断图中三角形的三边长是否满足 a2+b2=c2.由此: 你发现了什么规律?再见
练习
1.直角三角形两直角边长分别为5和 12,则它斜边上的高为_______.
2. 等腰△ABC的腰长AB=10cm,底BC为16cm,则底边上的高为 ,面积为 .
3.已知直角三角形中30°角所对的直角边长是cm,则另一条直角边的长是 ______.4。如图,在高2米,坡角为30°的楼梯表面铺地毯,地毯的长度至少需要_____米.
5.已知如图,水厂A和工厂B、C正好构成等边△ABC,现由水厂A和B、C两厂供水,要在A、B、C间铺设输水管道,有如下四种设计方案,(图中实线为铺设管道路线),其中最合理的方案是( )
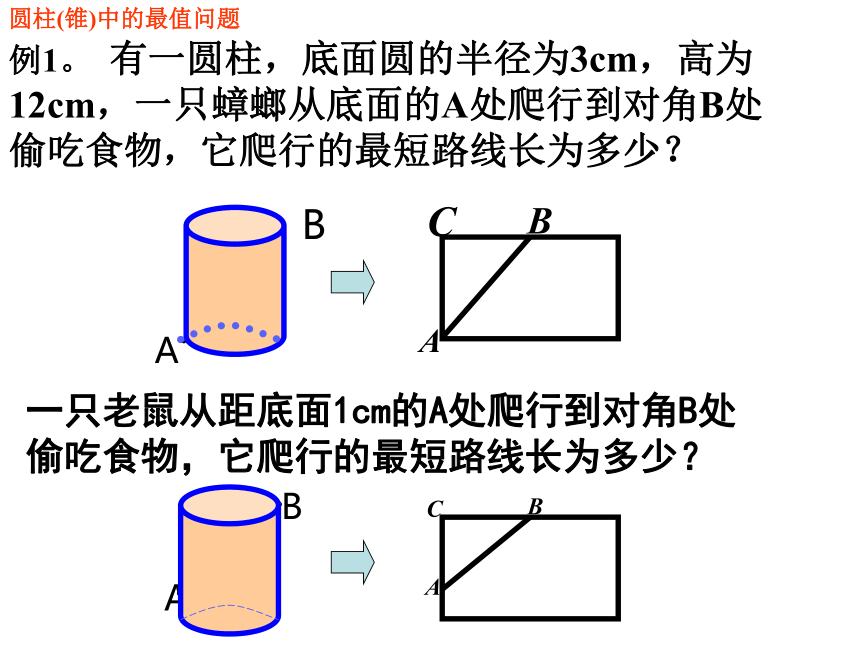
6. 如图,是2002年8月北京第24届国际数学家大会会标,由4个全等的直角三角形拼合而成.如果图中大、小正方形的面积分别为52和4,那么一个直角三角形的两直角边的和等于 .7.小刚准备测量河水的深度,他把一根竹竿插到离岸边1.5m远的水底,竹竿高出水面0.5m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,河水的深度为 .DA8。、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE圆柱(锥)中的最值问题例1。 有一圆柱,底面圆的半径为3cm,高为12cm,一只蟑螂从底面的A处爬行到对角B处
偷吃食物,它爬行的最短路线长为多少?AB一只老鼠从距底面1cm的A处爬行到对角B处
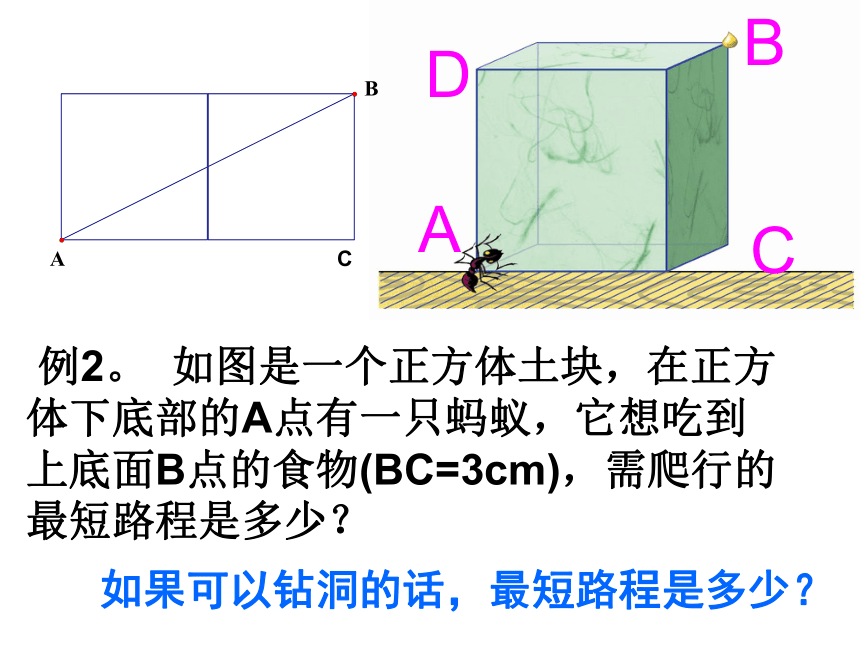
偷吃食物,它爬行的最短路线长为多少?AB 例2。 如图是一个正方体土块,在正方体下底部的A点有一只蚂蚁,它想吃到上底面B点的食物(BC=3cm),需爬行的最短路程是多少?BACDC如果可以钻洞的话,最短路程是多少? 如果盒子换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面需要爬行的最短路程又是多少呢? 变式分析:蚂蚁由A爬到B过程中较短的路线有多少种情况?(1)经过前面和上底面(2)经过前面和右面(3)经过下底面和右面 (1)当蚂蚁经过前面和上底面时,如图,最短路程为
AB= = =
(3)当蚂蚁经过下底面和右面时,如图,最短路程为
AB= = =
(2)当蚂蚁经过前面和右面时,如图,最短路程为
AB= =
=解:例3、如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?BA531512台阶中的最值问题∵ AB2=AC2+BC2=169,
∴ AB=13.练习1。在Rt△ABC中, ∠C=900,CD⊥AB于D, ∠A=600,CD= ,
求线段ABABCD2。在△ABC中,∠B=450,∠A=600,AC= 4
求线段ABABCD3。在四边形ABCD中, ∠A=600 , ∠B=∠D=900,AB= 4 ,CD=2
求:四边形ABCD的面积ABCDE 4。直角三角形的周长为30,斜边长为13,那么这个三角形的面积 为( )
A 15 B 30 C 60 D不能确定B 选一选5。已知,一轮船甲以16海里/时的速度从港口O出发向西北方向航行,另一轮船乙以12海里/时的速度同时从港口O出发向西南方向航行,离开港口2小时后,则两船相距( )
A、25海里 B、30海里 C、35海里 D、40海里
6。.台风是一种自然灾害,它以台风中心为圆心,在周围数十千米范围内形成气旋风暴,有极强的破坏力,据气象观测,距沿海某城市A的正南方向240km的B处有一台风中心,其中心风力为12级,每远离台风中心25km,风力就会减弱一级,该台风中心现正以20km/h的速度沿北偏东30°方向往C移动,如图所示,且台风中心的风力不变,若城市所受风力达到或超标四级,则称受台风影响.
(1)该城市是否受到台风影响?请说明理由;
(2)若会受到台风影响;那么台风影响该城市的持续时间有多长?
(3)该城市受到台风影响的最大风力为几级?7。如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?AB议一议 观察右图,用数格子的方法判断图中三角形的三边长是否满足 a2+b2=c2.由此: 你发现了什么规律?再见
