勾股定理的应用1[下学期]
文档属性
| 名称 | 勾股定理的应用1[下学期] |
|
|
| 格式 | rar | ||
| 文件大小 | 178.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-05-20 00:00:00 | ||
图片预览


文档简介
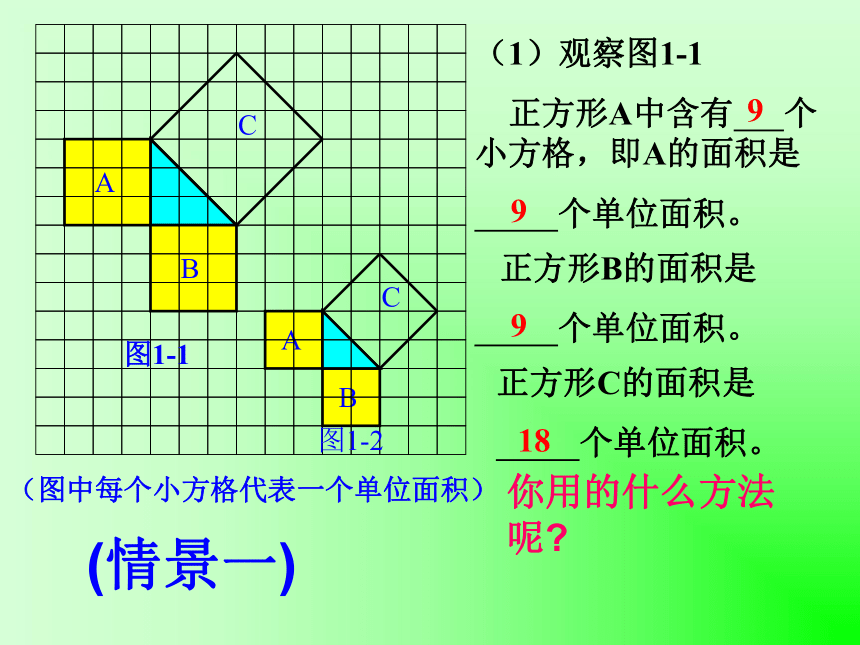
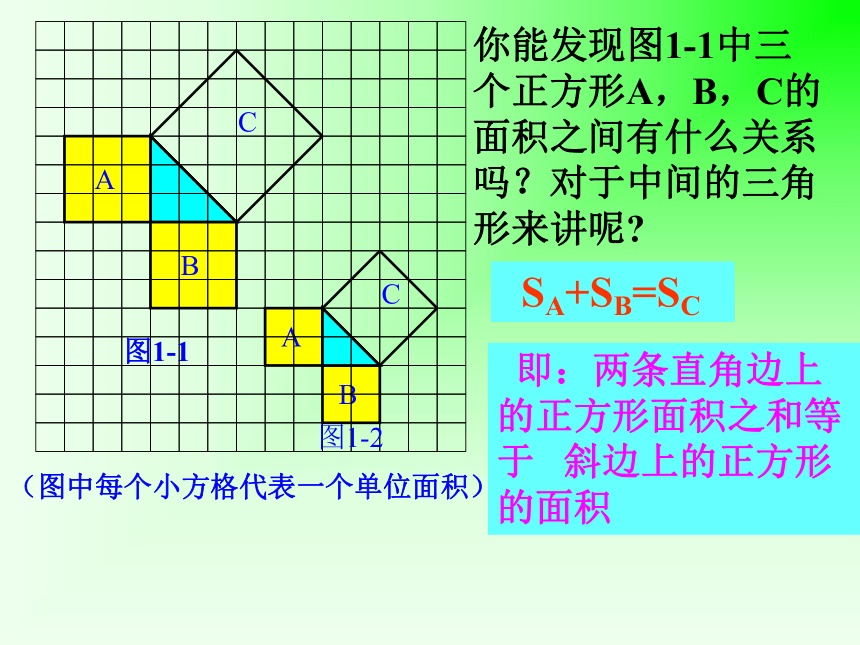
课件23张PPT。探索勾股定理涪陵十六中:湛小刚(1)观察图1-1
正方形A中含有 个小方格,即A的面积是
个单位面积。 正方形B的面积是
个单位面积。正方形C的面积是
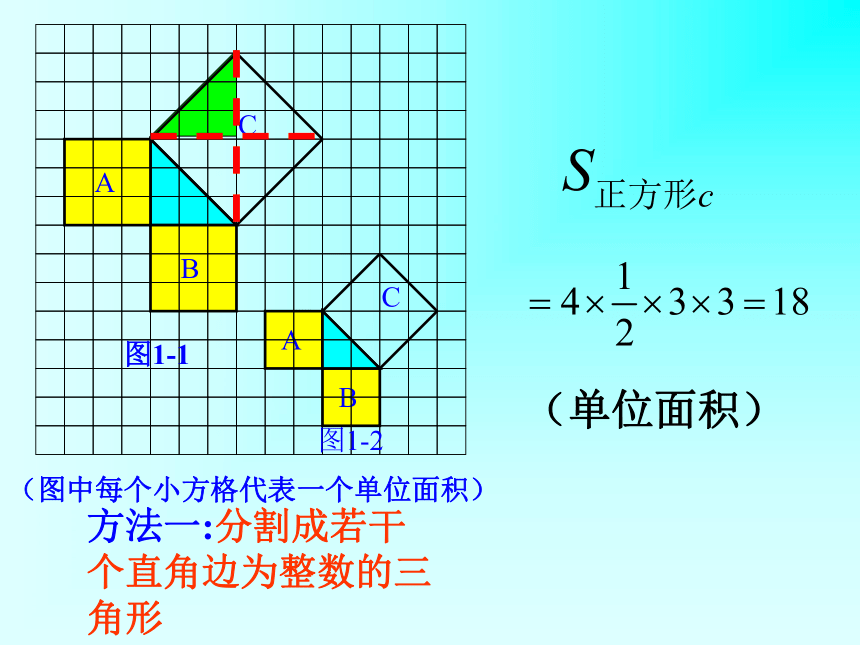
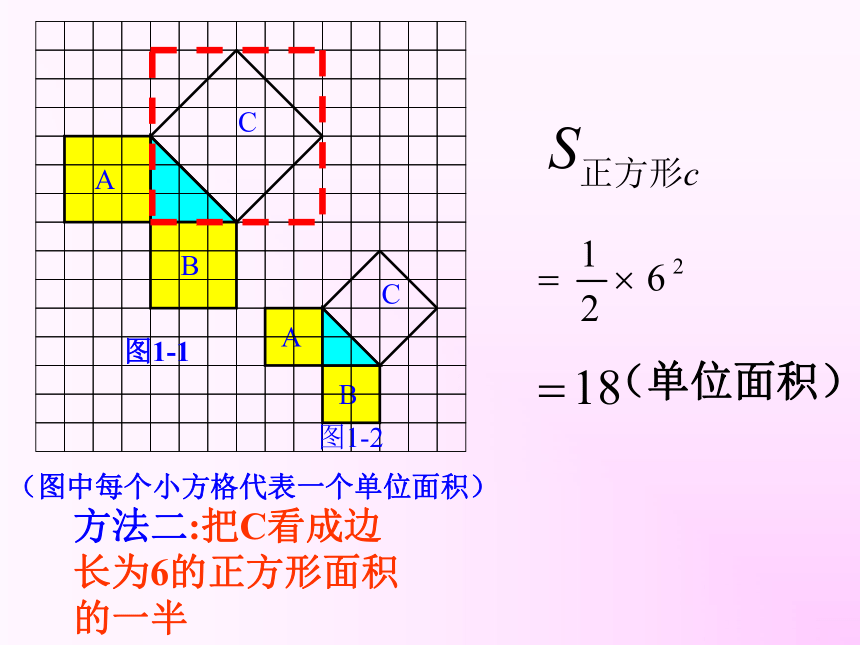
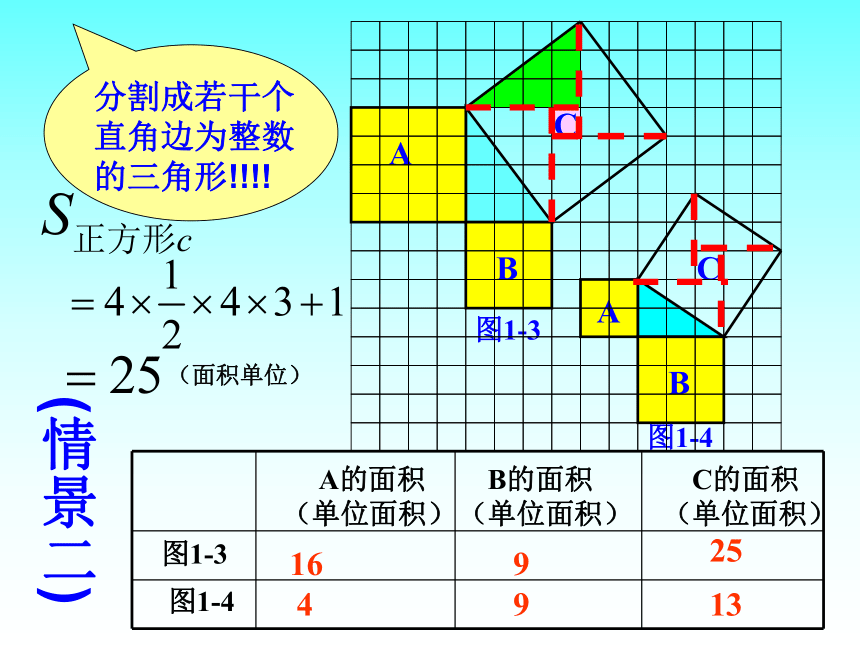
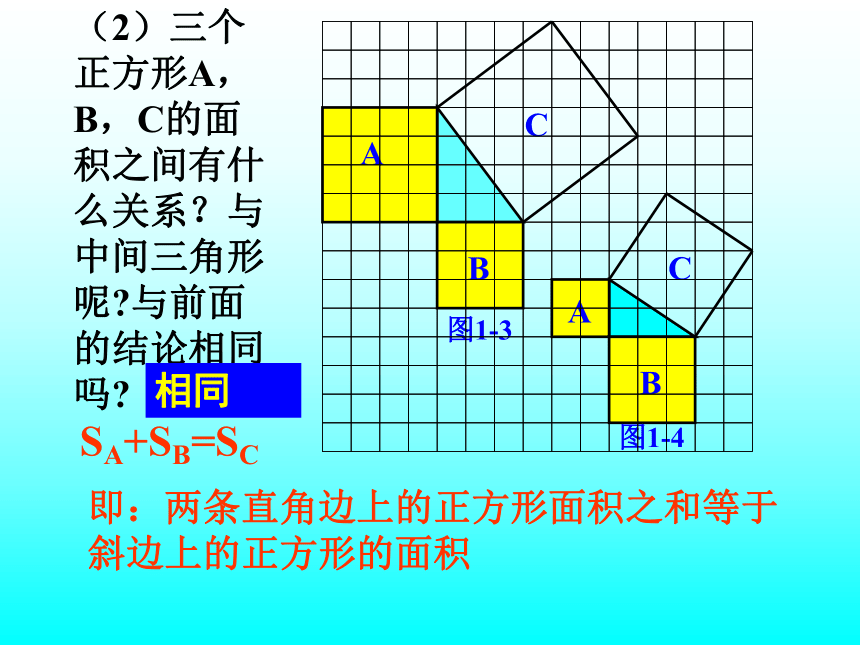
个单位面积。99918(情景一)你用的什么方法呢?方法一:分割成若干个直角边为整数的三角形(单位面积)(单位面积)方法二:把C看成边长为6的正方形面积的一半你能发现图1-1中三个正方形A,B,C的面积之间有什么关系吗?对于中间的三角形来讲呢? SA+SB=SC 即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积(面积单位)图1-3图1-4 A的面积(单位面积) B的面积(单位面积) C的面积(单位面积)169254913分割成若干个直角边为整数的三角形!!!!(情景二)(2)三个正方形A,B,C的面积之间有什么关系?与中间三角形呢?与前面的结论相同吗?SA+SB=SC
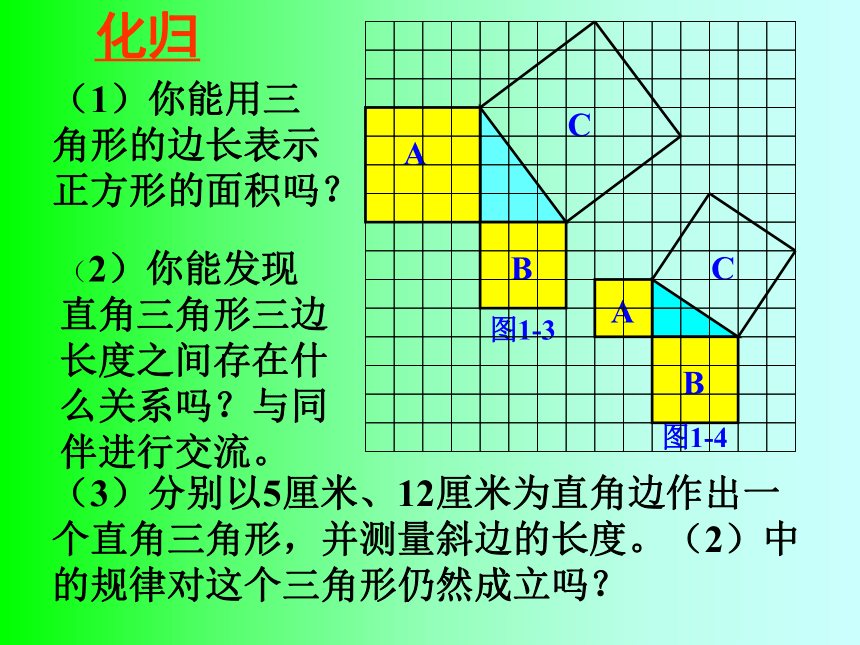
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积相同(1)你能用三角形的边长表示正方形的面积吗?(2)你能发现直角三角形三边长度之间存在什么关系吗?与同伴进行交流。(3)分别以5厘米、12厘米为直角边作出一个直角三角形,并测量斜边的长度。(2)中的规律对这个三角形仍然成立吗?化归 勾股定理: 如果直角三角形两直角边分别为a、b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。勾股弦世界上最先发现这个定理的人是我国的赵爽在△ABC中,∠C=90°.(1)若a=6,c=10,则b= ;(2)若a=12,b=9,则c = ;(3)若c=25,b=15,则 a = ;20(4)若c=10,a:b=3:4,则a=____,b=___. 68练习: 一判断题. 1.?ABC的两边AB=5,AC=12,则BC=13 ( ) 2.? ABC的a=6,b=8,则c=10 ( )二填空??没有注明到底是什么
三角形,所以是错误的在直角三角形中,一般a、b表示直边。C表示斜边三、如图,在Rt△ABC中, ∠C=90度,BC=24,AC=7,求AB的长.在Rt△ABC中,根据勾股定理解:(因为-25不合题意,故舍去)所以AB=25(变式)如果将题目变为:
在Rt△ABC中,AB=10, BC=8,求AC的长呢?ABCABC数学来源于生活, 又要服务到社会中去一、如图,要登上8米高的建筑物BC,为了安全需要,需使梯子底端离建筑物距离AB为6米,问至少需要多长的梯子?
8mBCA6m解:根据勾股定理得:
AC2= 62 + 82
=36+64
=100
即:AC= 10
(-10不合题意,故舍去)
所以AC=10(米)
答:梯子至少长10米。+_二、小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?∴售货员没搞错∵想一想荧屏对角线大约为74厘米三、如图,一根旗杆在“麦莎”飓风的作用下,离地面9米处断裂,旗杆顶部落在离旗杆底部12米处,旗杆折断前有多高。
六、飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶正上方4千米处,过了20秒,飞机距离这个男孩子头顶5千米,飞机每小时飞行多少千米?
20秒后4 km5 km探究趣闻 在1876年一个周末的傍晚,在美国首都华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景……他走着走着,突然发现附近的一个小石凳上,有两个小孩正在聚精会神地谈论着什么,时而大声争论,时而小声探讨.由于好奇心驱使他循声向两个小孩走去,想搞清楚两个小孩到底在干什么.只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形……于是这位中年人不再散步,立即回家,潜心探讨小男孩给他留下的难题。他经过反复的思考与演算,终于弄清楚了其中的道理,并给出了简洁的证明方法。? ???? 1876年4月1日,他在《新英格兰教育日志》上发表了他对勾股定理的这一证法。? ??? 1881年,这位中年人—伽菲尔德就任美国第二十任总统。后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为:“总统”证法┐┐小结说说这节课你有什么收获?再见
正方形A中含有 个小方格,即A的面积是
个单位面积。 正方形B的面积是
个单位面积。正方形C的面积是
个单位面积。99918(情景一)你用的什么方法呢?方法一:分割成若干个直角边为整数的三角形(单位面积)(单位面积)方法二:把C看成边长为6的正方形面积的一半你能发现图1-1中三个正方形A,B,C的面积之间有什么关系吗?对于中间的三角形来讲呢? SA+SB=SC 即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积(面积单位)图1-3图1-4 A的面积(单位面积) B的面积(单位面积) C的面积(单位面积)169254913分割成若干个直角边为整数的三角形!!!!(情景二)(2)三个正方形A,B,C的面积之间有什么关系?与中间三角形呢?与前面的结论相同吗?SA+SB=SC
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积相同(1)你能用三角形的边长表示正方形的面积吗?(2)你能发现直角三角形三边长度之间存在什么关系吗?与同伴进行交流。(3)分别以5厘米、12厘米为直角边作出一个直角三角形,并测量斜边的长度。(2)中的规律对这个三角形仍然成立吗?化归 勾股定理: 如果直角三角形两直角边分别为a、b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。勾股弦世界上最先发现这个定理的人是我国的赵爽在△ABC中,∠C=90°.(1)若a=6,c=10,则b= ;(2)若a=12,b=9,则c = ;(3)若c=25,b=15,则 a = ;20(4)若c=10,a:b=3:4,则a=____,b=___. 68练习: 一判断题. 1.?ABC的两边AB=5,AC=12,则BC=13 ( ) 2.? ABC的a=6,b=8,则c=10 ( )二填空??没有注明到底是什么
三角形,所以是错误的在直角三角形中,一般a、b表示直边。C表示斜边三、如图,在Rt△ABC中, ∠C=90度,BC=24,AC=7,求AB的长.在Rt△ABC中,根据勾股定理解:(因为-25不合题意,故舍去)所以AB=25(变式)如果将题目变为:
在Rt△ABC中,AB=10, BC=8,求AC的长呢?ABCABC数学来源于生活, 又要服务到社会中去一、如图,要登上8米高的建筑物BC,为了安全需要,需使梯子底端离建筑物距离AB为6米,问至少需要多长的梯子?
8mBCA6m解:根据勾股定理得:
AC2= 62 + 82
=36+64
=100
即:AC= 10
(-10不合题意,故舍去)
所以AC=10(米)
答:梯子至少长10米。+_二、小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?∴售货员没搞错∵想一想荧屏对角线大约为74厘米三、如图,一根旗杆在“麦莎”飓风的作用下,离地面9米处断裂,旗杆顶部落在离旗杆底部12米处,旗杆折断前有多高。
六、飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶正上方4千米处,过了20秒,飞机距离这个男孩子头顶5千米,飞机每小时飞行多少千米?
20秒后4 km5 km探究趣闻 在1876年一个周末的傍晚,在美国首都华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景……他走着走着,突然发现附近的一个小石凳上,有两个小孩正在聚精会神地谈论着什么,时而大声争论,时而小声探讨.由于好奇心驱使他循声向两个小孩走去,想搞清楚两个小孩到底在干什么.只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形……于是这位中年人不再散步,立即回家,潜心探讨小男孩给他留下的难题。他经过反复的思考与演算,终于弄清楚了其中的道理,并给出了简洁的证明方法。? ???? 1876年4月1日,他在《新英格兰教育日志》上发表了他对勾股定理的这一证法。? ??? 1881年,这位中年人—伽菲尔德就任美国第二十任总统。后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为:“总统”证法┐┐小结说说这节课你有什么收获?再见
