第七单元长方体和正方体整理复习(课件)-六年级上册数学苏教版(共33张PPT)
文档属性
| 名称 | 第七单元长方体和正方体整理复习(课件)-六年级上册数学苏教版(共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 991.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-19 16:46:55 | ||
图片预览










文档简介
(共33张PPT)
长方体、正方体整理复习
苏教版小学数学六年级下册第七单元
你是从哪几个方面进行整理的?
每个方面有哪些知识点?
交流要点:
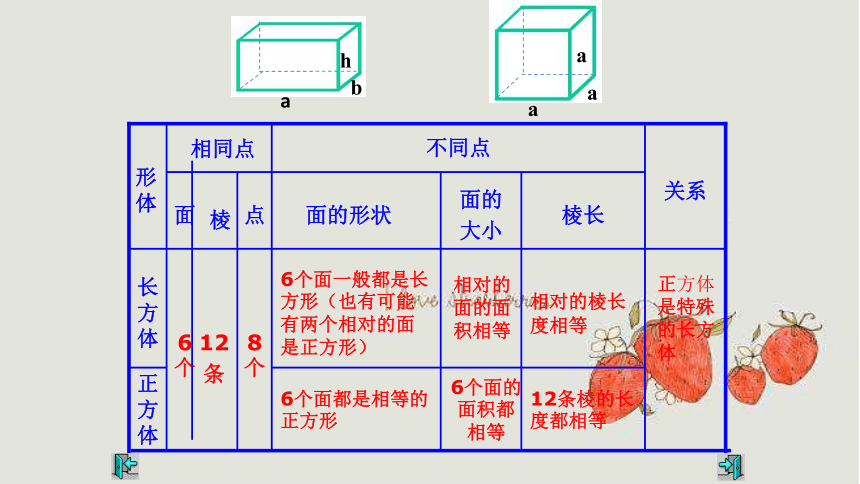
长方体和正方体有哪些特征?
说一说:
它们有哪些相同点和不同点?
8个
12
条
棱长
面的
大小
面的形状
点
棱
面
12条棱的长度都相等
6个面的面积都相等
6个面都是相等的正方形
正方体
正方体是特殊的长方体
相对的棱长度相等
相对的面的面积相等
6个面一般都是长方形(也有可能有两个相对的面是正方形)
6个
长方体
关系
不同点
相同点
形体
b
h
a
a
a
a
长方体或正方体表面积和体积的意义?
说一说:
表面积和体积的计算方法是什么?
1.( )叫做长方体或正方体的表面积。
2.长方体或正方体的体积( )
长、正方体6个面的总面积
长、正方体所占空间的大小。
名称 图形 表面积 体积
长方体
正方体
S=(ab+ah+bh)×2
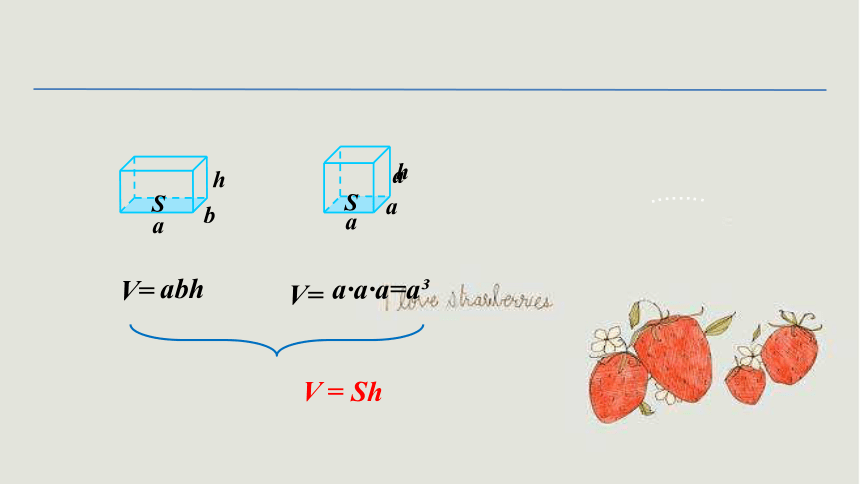
V=abh
S=6a2
V=a3
a
b
h
a
a
a
V=
ɑbh
V=
ɑ·ɑ·ɑ=ɑ
V = Sh
S
h
S
算一算:
一根长方体木料,长3米,横截面
是一个边长0.3米的正方形。这
根木料的横截面面积是多少平
方米?体积是多少立方米?
0.3×0.3=0.09(平方米)
0.09×3=0.27(立方米)
0.3米
3米
答:这根木料的横截面面积是0.09平方米。体积是0.27立方米。
我们学过哪些体积单位和容积单位?
说一说:
体积(容积)单位间的进率是怎样的?
1.( )常用的体积单位有。
2.常用的容积单位有
( )
立方厘米、立方分米、立方米
升、 毫升
1立方分米=1000立方厘米
1立方米=1000立方分米
相邻的两个体积单位间的进率都是
1000
1立方分米=1升
1立方厘米=1毫升
1升=1000毫升
相邻的两个容积单位间的进率都是
1000
3.05立方米=( )立方分米
0.8升=( )立方厘米
4500立方厘米=( )立方分米
60亳升=( )升
4.5
0.06
800
3050
填一填:
3.05×1000=
0.8×1000=
4500÷1000=
60÷1000=
实际生活中我们怎样求物体的表面积?
说一说:
超市售米用的木箱(上面没有盖),长1.2
米、宽1米、高0.8米。
1. 制作这样一个木箱至少要
用木板多少平方米?
2. 如果把木箱放在地上,占
地多少平方米?
3. 在木箱的四周贴上商标纸,
贴这个木箱要用商标纸多少
平方米?
一个无盖的长方体玻璃鱼缸,长5分米,宽4分米,高3分米。
(1)制作这个鱼缸至少需要玻璃多
少平方分米?
5×4+5×3×2+4×3 ×2
=20+30+24
=74(平方分米)
答:做这个鱼缸至少需要玻璃74平方分米。
一个无盖的长方体玻璃鱼缸,长5分米,宽4分米,高3分米。
(2)在鱼缸里注入40升水,水深多少分米?
40÷(5×4)
=40 ÷20
=2(分米)
答:水深2分米。
一个无盖的长方体玻璃鱼缸,长5分米,宽4分米,高3分米。
(3)再往水里放入一些鹅卵石,水面上升0.3分米,鹅卵石的体积一共多少立方分米?
5×4×0.3
=20×0.3
=6(立方分米)
答:鹅卵石的体积一共是6立方分米。
长、正方体棱长变化对表面积、体积变化有什么影响?
说一说:
正方体棱长扩大a倍,表面积扩大a2倍,体积扩大a3倍
长方体的长扩大a倍,宽扩大b倍,高扩大C倍,体积扩大a× b ×c的乘积倍。
长、正方体的展开图有什么特点?
说一说:
你能从不同角度观察立体图形吗?
你能找到其他的面在哪里吗?
前
后
上
下
左
右
如右图是由6个小立方体所搭几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数。
你能摆出这个几何体吗?
试画出这个几何体的正面与侧面看到的图形。
前面看:
左面看:
1
1
2
2
长方体或正方体切割拼合前后有关几何体表面积的变化有什么规律,你能用发现的规律解决一些简单实际问题吗?
说一说:
(如图)把这个长方体平均分成三个相等的小长方体,表面积增加了多少平方厘米?
3厘米
9厘米
6厘米
9厘米
3厘米
6厘米
9厘米
3厘米
6厘米
9厘米
3厘米
6厘米
把3个相同的正方体拼成一个长方体它的表面积有什么变化?
表面积减少了4个正方形的面积。
把八个棱长为1厘米的小正方体拼成一个长方体,有几种拼法?
★
28cm2
34cm2
24cm2
判断:
长方体中可以有两个面是正方形。
( )
② 3x=x·x·x ( )
用同样的小正方体拼成一个大正方
体,最少要用8个这样的小正方体。
( )
√
×
√
判断:
棱长为6厘米的正方体表面积和体积
相等。 ( )
4000平方分米=4平方米。
( )
⑥ 一个正方体的棱长是原来的2倍,
它的体积就是原来的4倍。 ( )
×
×
×
动脑筋:一个长方体,如果高增加2厘米,就变成一个正方体。这时表面积比原来增加56平方厘米。原来长方体的体积是多少立方厘米?
56÷4÷2=7(厘米)
7-2=5(厘米)
7×7×5=245(立方厘米)
答:原长方体的体积是245立方厘米。
长方体、正方体整理复习
苏教版小学数学六年级下册第七单元
你是从哪几个方面进行整理的?
每个方面有哪些知识点?
交流要点:
长方体和正方体有哪些特征?
说一说:
它们有哪些相同点和不同点?
8个
12
条
棱长
面的
大小
面的形状
点
棱
面
12条棱的长度都相等
6个面的面积都相等
6个面都是相等的正方形
正方体
正方体是特殊的长方体
相对的棱长度相等
相对的面的面积相等
6个面一般都是长方形(也有可能有两个相对的面是正方形)
6个
长方体
关系
不同点
相同点
形体
b
h
a
a
a
a
长方体或正方体表面积和体积的意义?
说一说:
表面积和体积的计算方法是什么?
1.( )叫做长方体或正方体的表面积。
2.长方体或正方体的体积( )
长、正方体6个面的总面积
长、正方体所占空间的大小。
名称 图形 表面积 体积
长方体
正方体
S=(ab+ah+bh)×2
V=abh
S=6a2
V=a3
a
b
h
a
a
a
V=
ɑbh
V=
ɑ·ɑ·ɑ=ɑ
V = Sh
S
h
S
算一算:
一根长方体木料,长3米,横截面
是一个边长0.3米的正方形。这
根木料的横截面面积是多少平
方米?体积是多少立方米?
0.3×0.3=0.09(平方米)
0.09×3=0.27(立方米)
0.3米
3米
答:这根木料的横截面面积是0.09平方米。体积是0.27立方米。
我们学过哪些体积单位和容积单位?
说一说:
体积(容积)单位间的进率是怎样的?
1.( )常用的体积单位有。
2.常用的容积单位有
( )
立方厘米、立方分米、立方米
升、 毫升
1立方分米=1000立方厘米
1立方米=1000立方分米
相邻的两个体积单位间的进率都是
1000
1立方分米=1升
1立方厘米=1毫升
1升=1000毫升
相邻的两个容积单位间的进率都是
1000
3.05立方米=( )立方分米
0.8升=( )立方厘米
4500立方厘米=( )立方分米
60亳升=( )升
4.5
0.06
800
3050
填一填:
3.05×1000=
0.8×1000=
4500÷1000=
60÷1000=
实际生活中我们怎样求物体的表面积?
说一说:
超市售米用的木箱(上面没有盖),长1.2
米、宽1米、高0.8米。
1. 制作这样一个木箱至少要
用木板多少平方米?
2. 如果把木箱放在地上,占
地多少平方米?
3. 在木箱的四周贴上商标纸,
贴这个木箱要用商标纸多少
平方米?
一个无盖的长方体玻璃鱼缸,长5分米,宽4分米,高3分米。
(1)制作这个鱼缸至少需要玻璃多
少平方分米?
5×4+5×3×2+4×3 ×2
=20+30+24
=74(平方分米)
答:做这个鱼缸至少需要玻璃74平方分米。
一个无盖的长方体玻璃鱼缸,长5分米,宽4分米,高3分米。
(2)在鱼缸里注入40升水,水深多少分米?
40÷(5×4)
=40 ÷20
=2(分米)
答:水深2分米。
一个无盖的长方体玻璃鱼缸,长5分米,宽4分米,高3分米。
(3)再往水里放入一些鹅卵石,水面上升0.3分米,鹅卵石的体积一共多少立方分米?
5×4×0.3
=20×0.3
=6(立方分米)
答:鹅卵石的体积一共是6立方分米。
长、正方体棱长变化对表面积、体积变化有什么影响?
说一说:
正方体棱长扩大a倍,表面积扩大a2倍,体积扩大a3倍
长方体的长扩大a倍,宽扩大b倍,高扩大C倍,体积扩大a× b ×c的乘积倍。
长、正方体的展开图有什么特点?
说一说:
你能从不同角度观察立体图形吗?
你能找到其他的面在哪里吗?
前
后
上
下
左
右
如右图是由6个小立方体所搭几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数。
你能摆出这个几何体吗?
试画出这个几何体的正面与侧面看到的图形。
前面看:
左面看:
1
1
2
2
长方体或正方体切割拼合前后有关几何体表面积的变化有什么规律,你能用发现的规律解决一些简单实际问题吗?
说一说:
(如图)把这个长方体平均分成三个相等的小长方体,表面积增加了多少平方厘米?
3厘米
9厘米
6厘米
9厘米
3厘米
6厘米
9厘米
3厘米
6厘米
9厘米
3厘米
6厘米
把3个相同的正方体拼成一个长方体它的表面积有什么变化?
表面积减少了4个正方形的面积。
把八个棱长为1厘米的小正方体拼成一个长方体,有几种拼法?
★
28cm2
34cm2
24cm2
判断:
长方体中可以有两个面是正方形。
( )
② 3x=x·x·x ( )
用同样的小正方体拼成一个大正方
体,最少要用8个这样的小正方体。
( )
√
×
√
判断:
棱长为6厘米的正方体表面积和体积
相等。 ( )
4000平方分米=4平方米。
( )
⑥ 一个正方体的棱长是原来的2倍,
它的体积就是原来的4倍。 ( )
×
×
×
动脑筋:一个长方体,如果高增加2厘米,就变成一个正方体。这时表面积比原来增加56平方厘米。原来长方体的体积是多少立方厘米?
56÷4÷2=7(厘米)
7-2=5(厘米)
7×7×5=245(立方厘米)
答:原长方体的体积是245立方厘米。
