湖北黄冈市黄梅县 18.1勾股定理习题课[下学期]
文档属性
| 名称 | 湖北黄冈市黄梅县 18.1勾股定理习题课[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 306.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-13 16:32:00 | ||
图片预览


文档简介
课件48张PPT。18.1 勾股定理(3)黄梅县晋梅中学
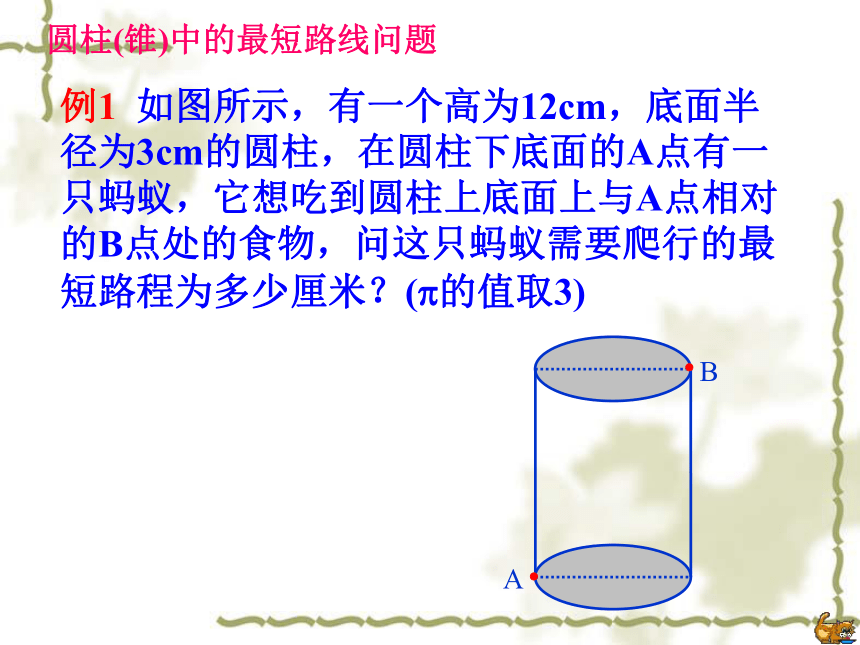
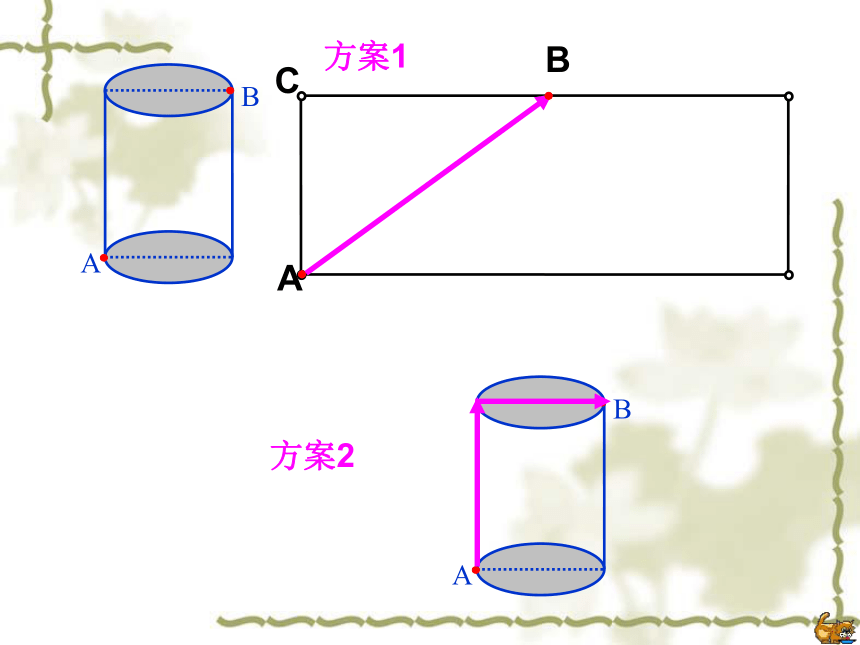
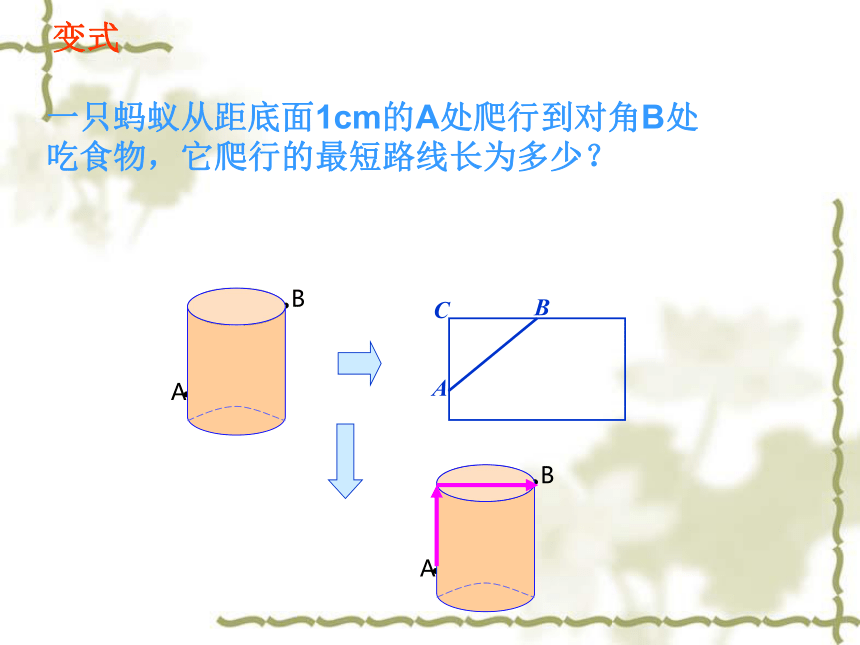
洪建明一、最短路线问题例1 如图所示,有一个高为12cm,底面半径为3cm的圆柱,在圆柱下底面的A点有一只蚂蚁,它想吃到圆柱上底面上与A点相对的B点处的食物,问这只蚂蚁需要爬行的最短路程为多少厘米?(?的值取3)圆柱(锥)中的最短路线问题B方案1方案2变式一只蚂蚁从距底面1cm的A处爬行到对角B处
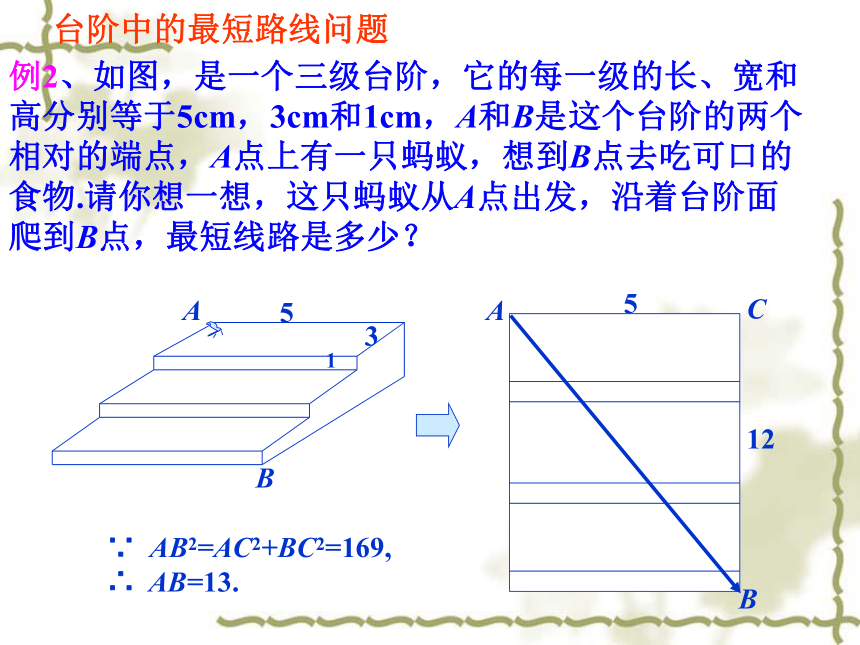
吃食物,它爬行的最短路线长为多少?ABAB例2、如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?BA531512台阶中的最短路线问题∵ AB2=AC2+BC2=169,
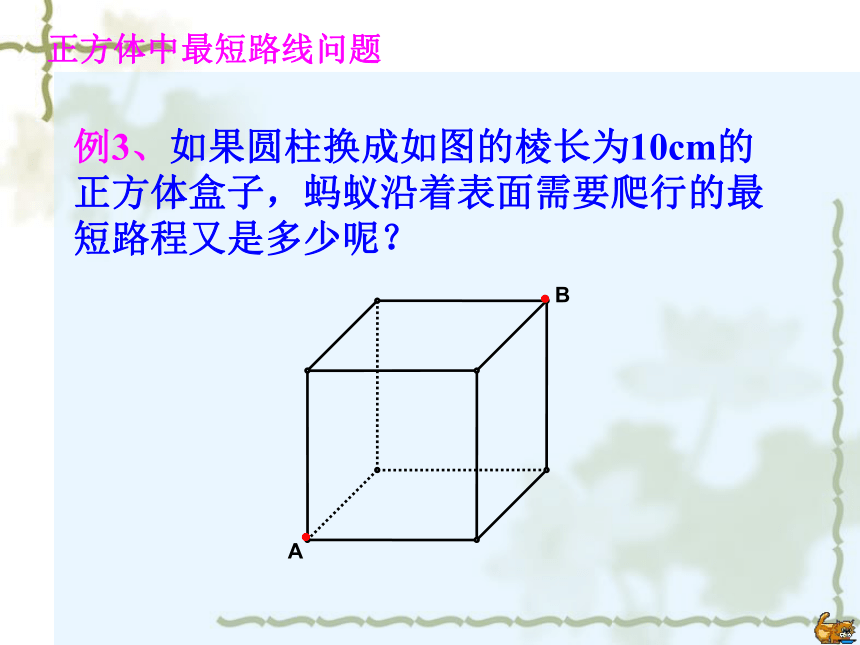
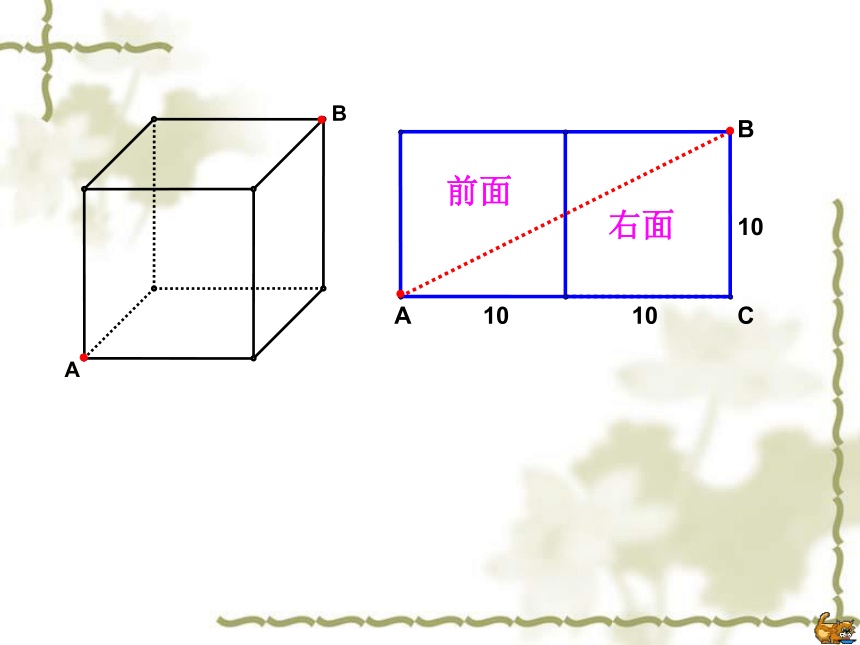
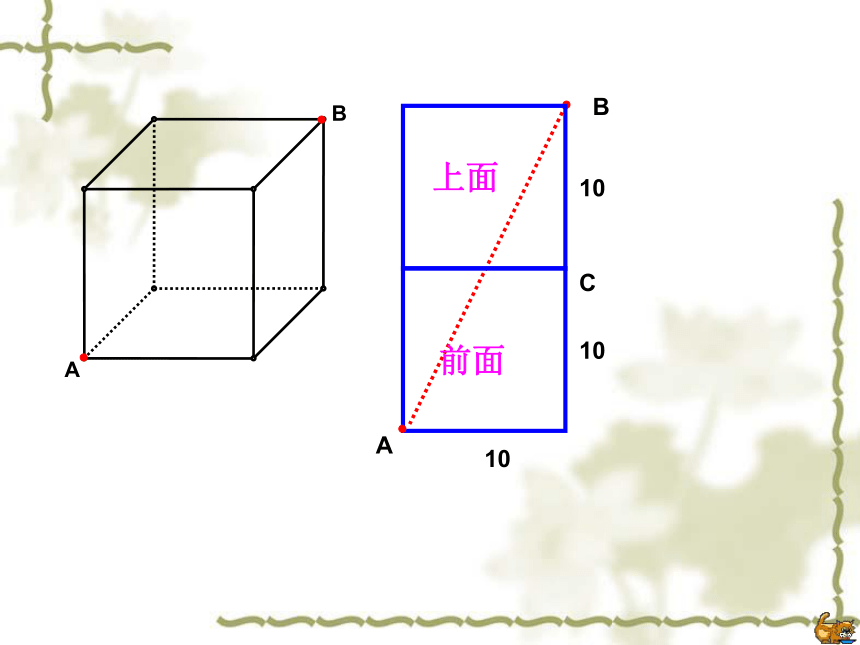
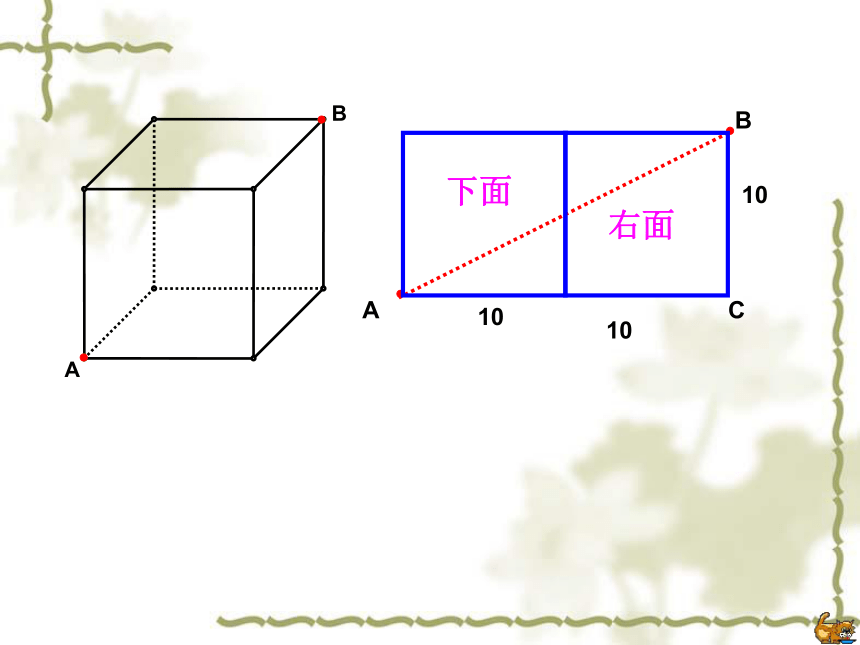
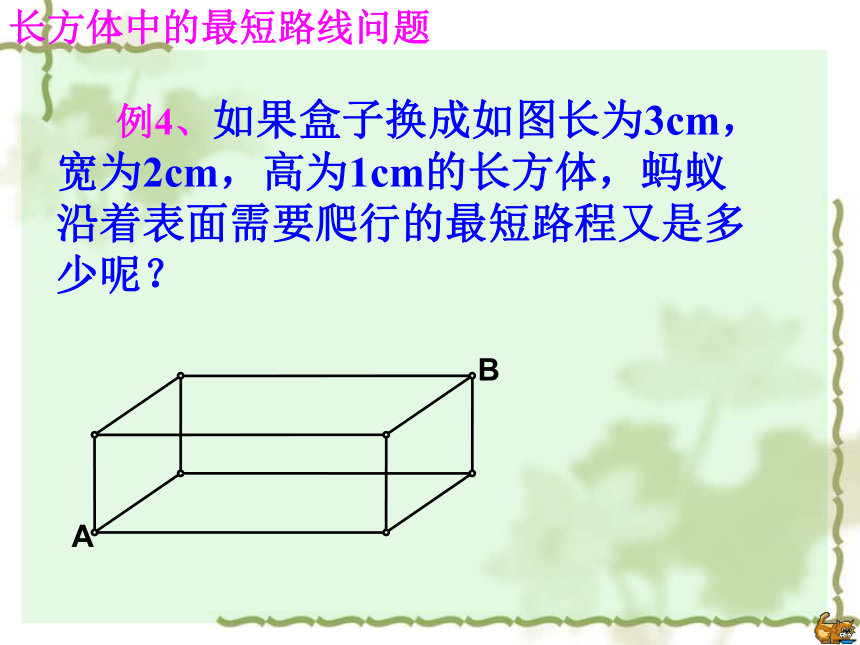
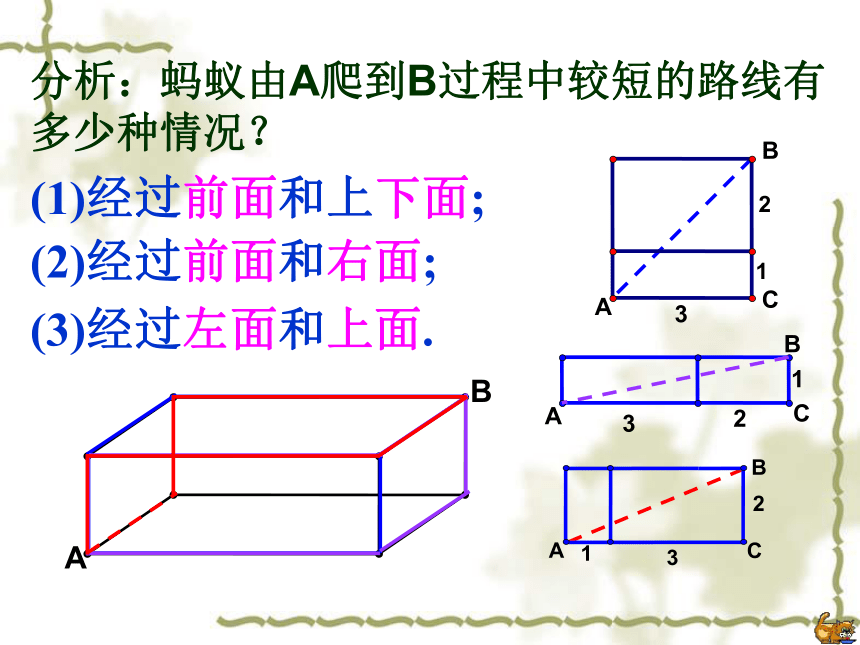
∴ AB=13.例3、如果圆柱换成如图的棱长为10cm的正方体盒子,蚂蚁沿着表面需要爬行的最短路程又是多少呢?正方体中最短路线问题前面右面1010BCA前面上面10101010BCA下面右面 例4、如果盒子换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面需要爬行的最短路程又是多少呢?长方体中的最短路线问题分析:蚂蚁由A爬到B过程中较短的路线有多少种情况?(1)经过前面和上下面;(2)经过前面和右面;(3)经过左面和上面. (1)当蚂蚁经过前面和上面时,如图,最短路程为解:AB===(2)当蚂蚁经过左面和上面时,如图,最短路程为AB===(3)当蚂蚁经过前面和右面时,如图,最短路程为AB===①②③观察下列哪个距离最小?你发现了什么? 如果长方形的长、宽、高分别是a、b、c(a>b>c),则从顶点A到B的最短线是:
如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?练习从A到C1的最短路径是变式练习:
如图,长方形中AC=3,CD=5,DF=6,求蚂蚁沿表面从A爬到F的最短距离.(二)、折叠四边形例5:矩形ABCD如图折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,求折痕AE的长。ABCDFE810106x8-x4x例6:折叠矩形纸片,先折出折痕对角线BD,在绕点D折叠,使点A落在BD的E处,折痕DG,若AB=2,BC=1,求AG的长。DAGBCE211BD=1X2-XX-1例7:边长为8和4的矩形OABC的两边分别在直角坐标系的X轴和Y轴上,若 沿对角线AC折叠后,点B落在第四象限B1处,设B1C交X轴于点D,求
(1)三角形ADC的面积;
(2)点B1的坐标;
(3)AB1所在的
直线解析式。E(三)折叠三角形例8、如图,小颍同学折叠一个直角三角形
的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?CABDE610-xx10-x例9:三角形ABC是等腰三角形AB=AC=13,BC=10,将AB向AC方向对折,再将CD折叠到CA边上,折痕CE,求三角形ACE的面积ABCDADCDCAD1E131213131266x67x12-x引申:勾股定理的拓展训 练四1.如图,在四边形ABCD中,∠BAD =900,∠DBC = 900 , AD = 3,AB = 4,BC = 12, 求CD;
2.已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,求四边形ABCD的面积。3、在等腰△ABC中,AB=AC=13cm ,BC=10cm,求△ABC的面积和AC边上的高。ABCD131310H提示:利用面积相等的关系4、 已知等边三角形ABC的边长是6cm,(1)求高AD的长;(2)S△ABC解:(1)∵△ABC是等边三角形,AD是高在Rt△ABD中,根据勾股定理5、 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。解:∵∠ABD=90°,∠DAB=30°∴BD= AD=4在Rt△ABD中,根据勾股定理在Rt△ABC中,又AD=8 6、 如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD证明:过A作AE⊥BC于EE∵AB=AC,∴BE=CE在Rt △ADE中,AD2=AE2+DE2在Rt △ABE中,AB2=AE2+BE2∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)= DE2- BE2= (DE+BE)·( DE- BE)= (DE+CE)·( DE- BE)=BD·CD7. 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水截面是一个边长为10尺的正方形.在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各为多少?解:设水池的水深AC为x尺,则这根芦苇长AD=AB=(x+1)尺,在直角三角形ABC中,BC=5尺由勾股定理得,BC2+AC2=AB2即 52+ x2= (x+1)225+ x2= x2+2 x+1,2 x=24,∴ x=12, x+1=13答:水池的水深12尺,这根芦苇长13尺。 8.如图,一只蚂蚁从0点出发,向正东方向走3米到达A1点,再向正北方向走6米到达A2点,再向正西方向走9米到达A3,再向正南方向走12米到达A4点,再向正东方向走15米到达A5点,按如此规律走,蚂蚁走到A6点时,离0点的距离是多少??? 挑战“试一试”:
9、一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门?说明理由。 2米2.3米OC┏D分析H2米2.3米 由于厂门宽度足够,所以卡车能否通过,只要看当卡车位于厂门正中间时其高度是否小于CH.如图所示,点D在离厂门中线0.8米处,且CD⊥AB, 与地面交于H.解CD=CH=0.6+2.3=2.9(米)>2.5(米).因此高度上有0.4米的余量,所以卡车能通过厂门.在Rt△OCD中,由勾股定理得==0.6米,2米2.3米10:细心观察,认真分析,回答问题:(1)用含有n的等式表示这个变化规律;
(2)推算OA10的长;
(3)求S12+S22+S32+….+S10211、小溪边长着两棵树,恰好隔岸相望,一棵树高30尺,另外一棵树高20尺;两棵树干间的距离是50尺,每棵树上都停着一只鸟,忽然两只鸟同时看到两树间水面上游出一条鱼,它们立刻以同样的速度飞去抓鱼,结果同时到达目标。问这条鱼出现在两树之间的何处?12、如图,等边三角形的边长是2。
(1)求高AD的长;
(2)求这个三角形的面积。若等边三角形的边长是a呢?13、如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积。14、如图,在△ABC中,∠ACB=900,AB=50cm,BC=30cm,CD⊥AB于D,求CD的长。15、已知,一轮船以16海里/时的速度从港口A出发向西北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东北方向航行,离开港口2小时后,则两船相距( )
A、25海里 B、30海里
C、35海里 D、40海里 16、一个圆柱状的杯子,由内部测得其底面直径为4cm,高为10cm,现有一支12cm的吸管任意斜放于杯中,则吸管 _露出杯口外. (填“能”或“不能”) 17、放学以后,小红和小颖从学校分手,分别沿着东方向和南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为 ( )
A、600米 B、800米
C、1000米 D、不能确定
18、直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是 ( )
A、6厘米 B、 8厘米
C、 80/13厘米; D、 60/13厘米; CD补充练习:19:
如图,求矩形零件上两孔中心A、B的距离.?20:矩形ABCD中,AB=6,BC=8,先把它对折,折痕为EF,展开后再沿BG折叠,使A落在EF上的A1,求第二次折痕BG的长。ABCDEFA1G正三角形AA1B
洪建明一、最短路线问题例1 如图所示,有一个高为12cm,底面半径为3cm的圆柱,在圆柱下底面的A点有一只蚂蚁,它想吃到圆柱上底面上与A点相对的B点处的食物,问这只蚂蚁需要爬行的最短路程为多少厘米?(?的值取3)圆柱(锥)中的最短路线问题B方案1方案2变式一只蚂蚁从距底面1cm的A处爬行到对角B处
吃食物,它爬行的最短路线长为多少?ABAB例2、如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?BA531512台阶中的最短路线问题∵ AB2=AC2+BC2=169,
∴ AB=13.例3、如果圆柱换成如图的棱长为10cm的正方体盒子,蚂蚁沿着表面需要爬行的最短路程又是多少呢?正方体中最短路线问题前面右面1010BCA前面上面10101010BCA下面右面 例4、如果盒子换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面需要爬行的最短路程又是多少呢?长方体中的最短路线问题分析:蚂蚁由A爬到B过程中较短的路线有多少种情况?(1)经过前面和上下面;(2)经过前面和右面;(3)经过左面和上面. (1)当蚂蚁经过前面和上面时,如图,最短路程为解:AB===(2)当蚂蚁经过左面和上面时,如图,最短路程为AB===(3)当蚂蚁经过前面和右面时,如图,最短路程为AB===①②③观察下列哪个距离最小?你发现了什么? 如果长方形的长、宽、高分别是a、b、c(a>b>c),则从顶点A到B的最短线是:
如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?练习从A到C1的最短路径是变式练习:
如图,长方形中AC=3,CD=5,DF=6,求蚂蚁沿表面从A爬到F的最短距离.(二)、折叠四边形例5:矩形ABCD如图折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,求折痕AE的长。ABCDFE810106x8-x4x例6:折叠矩形纸片,先折出折痕对角线BD,在绕点D折叠,使点A落在BD的E处,折痕DG,若AB=2,BC=1,求AG的长。DAGBCE211BD=1X2-XX-1例7:边长为8和4的矩形OABC的两边分别在直角坐标系的X轴和Y轴上,若 沿对角线AC折叠后,点B落在第四象限B1处,设B1C交X轴于点D,求
(1)三角形ADC的面积;
(2)点B1的坐标;
(3)AB1所在的
直线解析式。E(三)折叠三角形例8、如图,小颍同学折叠一个直角三角形
的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?CABDE610-xx10-x例9:三角形ABC是等腰三角形AB=AC=13,BC=10,将AB向AC方向对折,再将CD折叠到CA边上,折痕CE,求三角形ACE的面积ABCDADCDCAD1E131213131266x67x12-x引申:勾股定理的拓展训 练四1.如图,在四边形ABCD中,∠BAD =900,∠DBC = 900 , AD = 3,AB = 4,BC = 12, 求CD;
2.已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,求四边形ABCD的面积。3、在等腰△ABC中,AB=AC=13cm ,BC=10cm,求△ABC的面积和AC边上的高。ABCD131310H提示:利用面积相等的关系4、 已知等边三角形ABC的边长是6cm,(1)求高AD的长;(2)S△ABC解:(1)∵△ABC是等边三角形,AD是高在Rt△ABD中,根据勾股定理5、 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。解:∵∠ABD=90°,∠DAB=30°∴BD= AD=4在Rt△ABD中,根据勾股定理在Rt△ABC中,又AD=8 6、 如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD证明:过A作AE⊥BC于EE∵AB=AC,∴BE=CE在Rt △ADE中,AD2=AE2+DE2在Rt △ABE中,AB2=AE2+BE2∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)= DE2- BE2= (DE+BE)·( DE- BE)= (DE+CE)·( DE- BE)=BD·CD7. 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水截面是一个边长为10尺的正方形.在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各为多少?解:设水池的水深AC为x尺,则这根芦苇长AD=AB=(x+1)尺,在直角三角形ABC中,BC=5尺由勾股定理得,BC2+AC2=AB2即 52+ x2= (x+1)225+ x2= x2+2 x+1,2 x=24,∴ x=12, x+1=13答:水池的水深12尺,这根芦苇长13尺。 8.如图,一只蚂蚁从0点出发,向正东方向走3米到达A1点,再向正北方向走6米到达A2点,再向正西方向走9米到达A3,再向正南方向走12米到达A4点,再向正东方向走15米到达A5点,按如此规律走,蚂蚁走到A6点时,离0点的距离是多少??? 挑战“试一试”:
9、一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门?说明理由。 2米2.3米OC┏D分析H2米2.3米 由于厂门宽度足够,所以卡车能否通过,只要看当卡车位于厂门正中间时其高度是否小于CH.如图所示,点D在离厂门中线0.8米处,且CD⊥AB, 与地面交于H.解CD=CH=0.6+2.3=2.9(米)>2.5(米).因此高度上有0.4米的余量,所以卡车能通过厂门.在Rt△OCD中,由勾股定理得==0.6米,2米2.3米10:细心观察,认真分析,回答问题:(1)用含有n的等式表示这个变化规律;
(2)推算OA10的长;
(3)求S12+S22+S32+….+S10211、小溪边长着两棵树,恰好隔岸相望,一棵树高30尺,另外一棵树高20尺;两棵树干间的距离是50尺,每棵树上都停着一只鸟,忽然两只鸟同时看到两树间水面上游出一条鱼,它们立刻以同样的速度飞去抓鱼,结果同时到达目标。问这条鱼出现在两树之间的何处?12、如图,等边三角形的边长是2。
(1)求高AD的长;
(2)求这个三角形的面积。若等边三角形的边长是a呢?13、如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积。14、如图,在△ABC中,∠ACB=900,AB=50cm,BC=30cm,CD⊥AB于D,求CD的长。15、已知,一轮船以16海里/时的速度从港口A出发向西北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东北方向航行,离开港口2小时后,则两船相距( )
A、25海里 B、30海里
C、35海里 D、40海里 16、一个圆柱状的杯子,由内部测得其底面直径为4cm,高为10cm,现有一支12cm的吸管任意斜放于杯中,则吸管 _露出杯口外. (填“能”或“不能”) 17、放学以后,小红和小颖从学校分手,分别沿着东方向和南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为 ( )
A、600米 B、800米
C、1000米 D、不能确定
18、直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是 ( )
A、6厘米 B、 8厘米
C、 80/13厘米; D、 60/13厘米; CD补充练习:19:
如图,求矩形零件上两孔中心A、B的距离.?20:矩形ABCD中,AB=6,BC=8,先把它对折,折痕为EF,展开后再沿BG折叠,使A落在EF上的A1,求第二次折痕BG的长。ABCDEFA1G正三角形AA1B
