数学人教A版(2019)必修第一册4.5.1函数的零点与方程的解 课件(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.5.1函数的零点与方程的解 课件(共20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 847.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-19 19:38:08 | ||
图片预览








文档简介
(共20张PPT)
函数的零点与方程的解
在“函数的应用(一)”中,通过一些实例,我们初步了解了建立函数模型解决实际问题的过程,学习了用函数描述客观事物变化规律的方法,体会了函数作为解决数学问题的基本工具的重要性。本章我们将继续探究和学习运用函数性质求方程近似解的基本方法以及用函数构建数学模型的基本过程。首先我们来探究函数的零点与方程的解之间的关系。
一、整体感知,明确任务
判断下列方程是否有实数解?若有,是否有求根公式?
二、问题引入
三、回顾数学史展望课堂
回顾数学的发展史,古今中外的数学家们对方程的求解进行了一系列的探索,并取得了骄人的成绩。
约公元50~100年编成的《九章算术》记载了一次方程、二次方程、三次方程的求根方法;
南宋数学家秦九韶在《数书九章》中提出了“正负开方术”,提供了一种用算筹布列解任意数字方程的有效算法,此法可以求出任意次代数方程的正跟
三、回顾数学史展望课堂
9世纪,阿拉伯数学家花啦子米(Al-Khowarizmi,约780-850)给出了一次方程和二次方程的一般解法。
1541年,意大利数学家塔尔塔利亚(N.Tartaglia,约1499-1557)给出了三次方程的一般解法;1545 年,意大利数学家卡尔达诺(G.Cardano,1501-1576)的名著 《大术》一书中,把塔尔塔利亚的解法加以发展,并记载了费拉里(LFerrari,1522-1565)的四次方程的一般解法。
例如:一元二次方程 的根是什么?它们和相应的二次函数
有什么关系?
一般地,一元二次方程的根就是对应的二次函数的零点,也就是二次函数的图像与x轴交点的横坐标。
四、函数的零点定义探究
问题1:如何从二次函数的角度认识一元二次方程的根?
四、函数的零点定义探究
方程 的解就是函数 的图像与 轴的交点的横坐标。
对于一般函数 ,我们把使 的实数 叫做函数 的零点。
追问1:函数的零点是点吗
函数的零点不是点,而是方程 的解,是一个实数。
问题2:类比以上结论,对于一般的方程 我们是否也能从函数 的角度来探究其解的情况?
能
函数的零点:
追问2:方程 的根、函数 的零点与函数 的图像三者之间的关系是什么?
方程 的根
函数 的零点
函数 的图像与
轴交点的横坐标
方程 的解问题
函数 的零点问题
函数 的图与 轴的交点问题
四、函数的零点定义探究
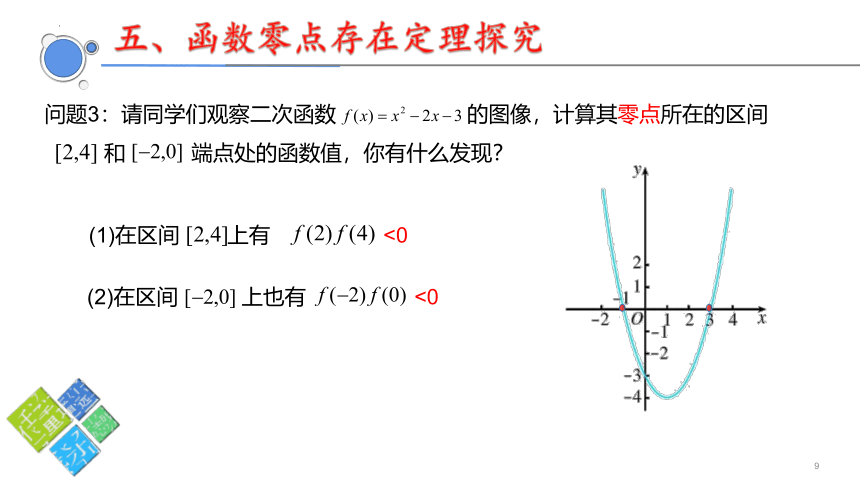
问题3:请同学们观察二次函数 的图像,计算其零点所在的区间
和 端点处的函数值,你有什么发现?
五、函数零点存在定理探究
(1)在区间 上有 <0
(2)在区间 上也有 <0
问题4:观察下列函数的图像,思考:对于一般的函数 ,在其零点所在的区
间 上 是否也有上面的结论?
a
b
x
y
五、函数零点存在定理探究
若保持端点处的函数值不变,请同学们尝试改变函数图像的形状,观察零点的变化情况,回答问题5,6?
①
②
③
④
⑤
①②③
④⑤
一个零点
三个零点
没有零点
是什么原因造成了没有零点?
问题5:当 时,函数 在区间 上的零点个数情况如何?
五、函数零点存在定理探究
图像不连续!
问题6:当 时函数 在区间 上的零点个数情况如何?
可能有零点,
也可能没有零点
五、函数零点存在定理探究
问题7:根据以上结论函数 满足什么条件时它在区间 上就一定有零点?
(2) 区间端点处的函数值异号,即
(1)函数 在区间 上的图象是一条连续不断的曲线;
函数零点存在定理:
如果函数 在区间 上的图象 ,且有 ,那么,函数 在区间 内一定有零点,即存在 ,使得 ,这个c也就是方程 的解。
五、函数零点存在定理探究
有几个零点呢?
至少有一个!
是一条连续不断的曲线
追问2:函数 在区间 上的图象是一条连续不断的曲线,且 ,是函数在区间 上有零点的什么条件?
充分不必要条件
五、函数零点存在定理探究
追问1:在零点存在定理的基础上再加上什么条件就能保证函数 在区间 上有且只有一个零点?
函数 在区间 上单调
六、初步应用,深化理解
例1. 函数 的零点所在的区间为( ).
C
例2.求方程 的实数解的个数.
六、初步应用,深化理解
方程的解个数
函数的零点的个数
函数零点存在定理
结合单调性
转化
运用定理
作图(函数图像与x轴的交点的个数)
数形结合
六、初步应用,深化理解
练习:方程 在区间 上的实数解的个数为( ).
B
七、课堂小结
方程
的根
函数
的零点
函数 的图像与
轴交点的横坐标
函数零点存在定理
1、课堂小结:
2、课堂感悟:
从特殊到一般抽象定义、归纳结论;根据定义(定理)再思考提出
问题辨析定义(定理);数形结合、转化化归解决问题。
转化
数形结合
八、课后作业与思考
作业:教材 习题 1,2
课后思考:我们已经知道函数 在区间(2,3)内有且只有一个零点,那么如何把零点所在的区间长度缩短?又如何求其零点的近似值呢?
谢谢 !
函数的零点与方程的解
在“函数的应用(一)”中,通过一些实例,我们初步了解了建立函数模型解决实际问题的过程,学习了用函数描述客观事物变化规律的方法,体会了函数作为解决数学问题的基本工具的重要性。本章我们将继续探究和学习运用函数性质求方程近似解的基本方法以及用函数构建数学模型的基本过程。首先我们来探究函数的零点与方程的解之间的关系。
一、整体感知,明确任务
判断下列方程是否有实数解?若有,是否有求根公式?
二、问题引入
三、回顾数学史展望课堂
回顾数学的发展史,古今中外的数学家们对方程的求解进行了一系列的探索,并取得了骄人的成绩。
约公元50~100年编成的《九章算术》记载了一次方程、二次方程、三次方程的求根方法;
南宋数学家秦九韶在《数书九章》中提出了“正负开方术”,提供了一种用算筹布列解任意数字方程的有效算法,此法可以求出任意次代数方程的正跟
三、回顾数学史展望课堂
9世纪,阿拉伯数学家花啦子米(Al-Khowarizmi,约780-850)给出了一次方程和二次方程的一般解法。
1541年,意大利数学家塔尔塔利亚(N.Tartaglia,约1499-1557)给出了三次方程的一般解法;1545 年,意大利数学家卡尔达诺(G.Cardano,1501-1576)的名著 《大术》一书中,把塔尔塔利亚的解法加以发展,并记载了费拉里(LFerrari,1522-1565)的四次方程的一般解法。
例如:一元二次方程 的根是什么?它们和相应的二次函数
有什么关系?
一般地,一元二次方程的根就是对应的二次函数的零点,也就是二次函数的图像与x轴交点的横坐标。
四、函数的零点定义探究
问题1:如何从二次函数的角度认识一元二次方程的根?
四、函数的零点定义探究
方程 的解就是函数 的图像与 轴的交点的横坐标。
对于一般函数 ,我们把使 的实数 叫做函数 的零点。
追问1:函数的零点是点吗
函数的零点不是点,而是方程 的解,是一个实数。
问题2:类比以上结论,对于一般的方程 我们是否也能从函数 的角度来探究其解的情况?
能
函数的零点:
追问2:方程 的根、函数 的零点与函数 的图像三者之间的关系是什么?
方程 的根
函数 的零点
函数 的图像与
轴交点的横坐标
方程 的解问题
函数 的零点问题
函数 的图与 轴的交点问题
四、函数的零点定义探究
问题3:请同学们观察二次函数 的图像,计算其零点所在的区间
和 端点处的函数值,你有什么发现?
五、函数零点存在定理探究
(1)在区间 上有 <0
(2)在区间 上也有 <0
问题4:观察下列函数的图像,思考:对于一般的函数 ,在其零点所在的区
间 上 是否也有上面的结论?
a
b
x
y
五、函数零点存在定理探究
若保持端点处的函数值不变,请同学们尝试改变函数图像的形状,观察零点的变化情况,回答问题5,6?
①
②
③
④
⑤
①②③
④⑤
一个零点
三个零点
没有零点
是什么原因造成了没有零点?
问题5:当 时,函数 在区间 上的零点个数情况如何?
五、函数零点存在定理探究
图像不连续!
问题6:当 时函数 在区间 上的零点个数情况如何?
可能有零点,
也可能没有零点
五、函数零点存在定理探究
问题7:根据以上结论函数 满足什么条件时它在区间 上就一定有零点?
(2) 区间端点处的函数值异号,即
(1)函数 在区间 上的图象是一条连续不断的曲线;
函数零点存在定理:
如果函数 在区间 上的图象 ,且有 ,那么,函数 在区间 内一定有零点,即存在 ,使得 ,这个c也就是方程 的解。
五、函数零点存在定理探究
有几个零点呢?
至少有一个!
是一条连续不断的曲线
追问2:函数 在区间 上的图象是一条连续不断的曲线,且 ,是函数在区间 上有零点的什么条件?
充分不必要条件
五、函数零点存在定理探究
追问1:在零点存在定理的基础上再加上什么条件就能保证函数 在区间 上有且只有一个零点?
函数 在区间 上单调
六、初步应用,深化理解
例1. 函数 的零点所在的区间为( ).
C
例2.求方程 的实数解的个数.
六、初步应用,深化理解
方程的解个数
函数的零点的个数
函数零点存在定理
结合单调性
转化
运用定理
作图(函数图像与x轴的交点的个数)
数形结合
六、初步应用,深化理解
练习:方程 在区间 上的实数解的个数为( ).
B
七、课堂小结
方程
的根
函数
的零点
函数 的图像与
轴交点的横坐标
函数零点存在定理
1、课堂小结:
2、课堂感悟:
从特殊到一般抽象定义、归纳结论;根据定义(定理)再思考提出
问题辨析定义(定理);数形结合、转化化归解决问题。
转化
数形结合
八、课后作业与思考
作业:教材 习题 1,2
课后思考:我们已经知道函数 在区间(2,3)内有且只有一个零点,那么如何把零点所在的区间长度缩短?又如何求其零点的近似值呢?
谢谢 !
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
