4.1.1 n次方根与分数指数幂 说课课件(共23张PPT)
文档属性
| 名称 | 4.1.1 n次方根与分数指数幂 说课课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-19 20:24:36 | ||
图片预览







文档简介
4.1 指数
4.1.1 ????次方根与分数指数幂
?
(一)了解背景,统领全章
问题1:请同学们先阅读教材第103页章头图与章引言,回答下面问题:
(1)本章将要学习的内容是什么?
(2)从文中你了解这些函数可以解决哪些实际问题?
(二)复习旧知,梳理路径
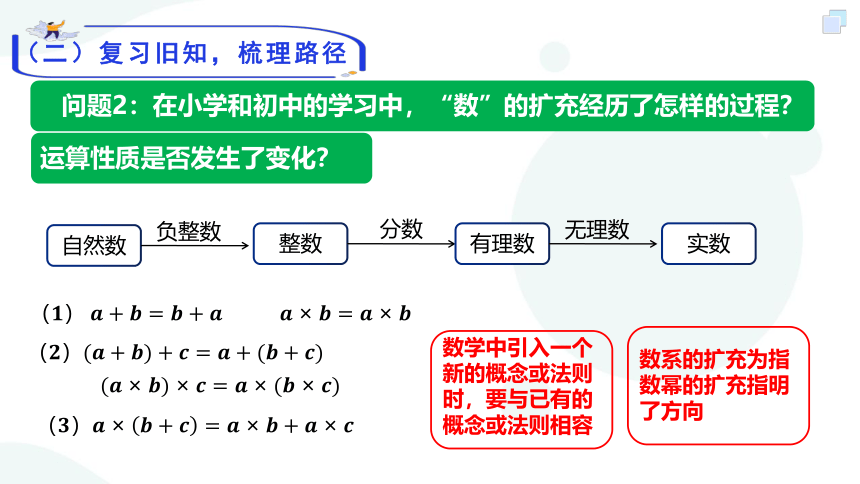
数学中引入一个新的概念或法则时,要与已有的概念或法则相容
问题2:在小学和初中的学习中,“数”的扩充经历了怎样的过程?
数系的扩充为指数幂的扩充指明了方向
(????) ????+????=????+???? ????×????=????×????
?
(????)????×????+????=????×????+????×????
?
(????)(????+????)+????=????+(????+????)
?
(????×????)×????=????×(????×????)
?
运算性质是否发生了变化?
自然数
负整数
整数
分数
有理数
无理数
实数
(二)复习旧知,梳理路径
(????)????????????????=????????+????(????>????,????,????∈?????);
(????)(????????)????=????????????(????>????,????,????∈?????);
(????)(????????)????=????????????????(????>????,????,????∈?????);
?
????????=????×????×????×??×????(????∈?????);
?
?????????=???? ????????(????∈?????);
?
(????)????????????????=????????+????(????>????,????,????∈????);
(????)(????????)????=????????????(????>????,????,????∈????);
(????)(????????)????=????????????????(????>????,????,????∈????);
?
问题3:谈到指数,在初中学习了正整数指数幂,你能说出正整数指数幂的意义和运算性质吗?
初中还把指数进行了扩充,使其可以取负整数,你能说出负整数指数幂意义是什么呢?
(二)复习旧知,梳理路径
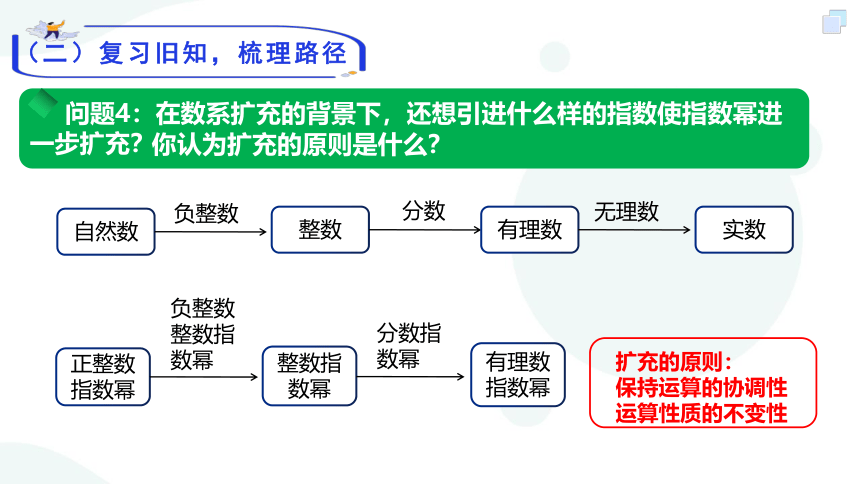
问题4:在数系扩充的背景下,还想引进什么样的指数使指数幂进一步扩充?
自然数
负整数
整数
分数
有理数
无理数
实数
正整数指数幂
负整数整数指数幂
整数指数幂
分数指数幂
有理数指数幂
扩充的原则:
保持运算的协调性
运算性质的不变性
你认为扩充的原则是什么?
(三)类比学习,形成概念
????=±????
?
????=3????
?
如果????????=????,那么????叫做????的平方根(二次方根).记作 ;
?
如果????????=????,那么????叫做????的立方根(三次方根).记作 ;
?
比如:±????????=????,那么±????叫做4的平方根.
?
比如:?????????=?????,那么?????叫做?8的立方根.
?
问题5:在初中我们由平方、立方的运算,引入了平方根、立方根。你能举例说明它们的概念吗?
(三)类比学习,形成概念
如果 ,那么????叫做????的四次方根.记作 ;
?
????4=????
?
????=±4????
?
如果 ,那么????叫做????的五次方根.记作 ;
?
????5=????
?
????=5????
?
如果 ,那么????叫做????的????次方根.其中????>????,且????∈????? .
?
????????=????
?
追问1:类比二次方根、三次方根的定义,你能说出四次方根,五次方根的定义吗?
追问2:你能归纳出更一般的n次方根的定义吗?并举例说明.
比如:±????????=????????,那么±????叫做64的6次方根.
?
(三)类比学习,形成概念
如果 ,那么????叫做????的二次方根.记作 ;
?
如果 ,那么????叫做????的五次方根.记作 ;
?
如果 ,那么????叫做????的四次方根.记作 ;
?
如果 ,那么????叫做????的三次方根.记作 ;
?
????2=????
?
????=±????
?
????3=????
?
????=3????
?
????4=????
?
????5=????
?
????=±4????
?
????=5????
?
追问3:讨论任意实数????都有n次方根吗?有几个?该如何表示实数????的n次方根?可以举例说明.
?
如果 ,那么????叫做????的????次方根.其中????>????,且????∈????? .
?
????????=????
?
(三)类比学习,形成概念
分????为奇数与偶数
分????为正数、负数、零
?
????????叫做根式,
????叫做根指数,
????叫做被开方数
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
????为奇数
????为偶数
????>????
????????=????
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
存在,有一个,是正数????????
?
存在,有两个,是相反数±????????
?
存在,有一个,是负数????????
?
不存在
????????=????
?
比如:
10的5次方根是_______;
10的6次方根是________;
????(????>????)的6次方根是______;
????????(????>????)的7次方根是_____;
?
510
?
±610
?
±6????
?
7????2
?
(四)回归定义,发现性质
问题6:回顾二次根式的学习过程,我们先定义了二次根式,又探究了二次根式的性质(????)????=????,????????=????,那么n次根式有什么性质呢?
?
(四)回归定义,发现性质
????
?
????
?
????
?
?????
?
?????
?
问题6:回顾二次根式的学习过程,我们先定义了二次根式,又探究了二次根式的性质(????)????=????,????????=????,那么n次根式有什么性质呢?
?
(????????)????=????
?
追问:根据(????)????=????,你认为????次根式????????有什么类似性质?
?
(四)回归定义,感悟性质
追问:根据????????=????,你认为????次根式????????也有这样的性质吗?
?
????
?
????
?
????
?
????
?
????
?
?????
?
????
?
?????
?
根据运算中地不变性,得出
????????????=
?
计算下列根式的值?
????,????为奇数????,????为偶数
?
(五)深思熟虑,深化概念
例1.利用????次方根的性质,计算下列值
?
追问:观察????????????????=????????,2与5,10之间有什么关系?
????????????????=????????,3与4,12之间有什么关系?
?
当根式的被开方数的指数能被根指数整除时,
根式可以表示为分数指数幂的形式.
5????25=????2
?
4????34=??3
?
=????????????????
?
由此你能得出什么结论?
=????????????????
?
=????????????×????????
?
=????????????????????
?
=????????????×????????=????????????????????
?
(五)深思熟虑,深化概念
问题7:当根式的被开方数的指数不能被根指数整除时,根式是否也可以表示为分数指数幂的形式?
????????????
?
????????????
?
????????????
?
????????????
?
????????????
?
????????=????
?
= ? ????
?
指数幂的运算性质不发生变化
????????????=????=(???????? ????)????
?
????????????=????=(????????????)????
?
????????????????=????????=(???????? ????)????
?
????????????????=????????=(???????? ????)????
?
(五)深思熟虑,深化概念
?????????????=_________ (????>??,????,????∈?????,????>????)
?
1????????????
?
0的正分数指数幂等于0,0负分数指数幂不存在
追问1:类比?????????=????????????(????∈????,????≠????),你能得到负分数指数幂的定义吗?
?
追问2:0的正分数指数幂等于几?0有负分数指数幂吗?
规定:正数的正分数指数幂????????????=_________ (????>????,????,????∈?????,????>????)
?
????????????
?
整数指数幂的运算性质确实对有理数指数幂的运算适用,我们用计算机来加以验证.
(????)????????????????=????????+????(????>????,????,????∈????);
(????)(????????)????=????????????(????>????,????,????∈????);
(????)(????????)????=????????????????(????>????,????,????∈????);
?
(五)深思熟虑,深化概念
有理数指数幂的其他性质(????>????,????∈????)
?
1.若????>????时,????????随????的增大而增大.
?
2.若?????
(六)巩固知识,典例应用
例2.求值
(六)巩固知识,典例应用
例3.用分数指数幂的形式表示并计算下列各式(其中????>????)
?
(七)归纳总结,强化思想
1.回顾本节的内容和学习过程谈谈你的收获?
n次方根
定义
表示
性质
根式
整数指数幂
有理数指数幂
分数指数幂
二次方根
三次方根
……
(七)归纳总结,强化思想
2.在数系扩充的背景下,你还希望将指数的范围如何扩充?扩充的原则是什么?
实数
有理数
整数
自然数
?
有理数指数幂
整数指数幂
正整数指数幂
(八)强化训练,布置作业
1.基础性作业
P107页1,2,3
P109页1,4
2.探究性作业
P110页拓广探索10题
3.课前任务
估算????的值
?
感谢聆听
4.1.1 ????次方根与分数指数幂
?
(一)了解背景,统领全章
问题1:请同学们先阅读教材第103页章头图与章引言,回答下面问题:
(1)本章将要学习的内容是什么?
(2)从文中你了解这些函数可以解决哪些实际问题?
(二)复习旧知,梳理路径
数学中引入一个新的概念或法则时,要与已有的概念或法则相容
问题2:在小学和初中的学习中,“数”的扩充经历了怎样的过程?
数系的扩充为指数幂的扩充指明了方向
(????) ????+????=????+???? ????×????=????×????
?
(????)????×????+????=????×????+????×????
?
(????)(????+????)+????=????+(????+????)
?
(????×????)×????=????×(????×????)
?
运算性质是否发生了变化?
自然数
负整数
整数
分数
有理数
无理数
实数
(二)复习旧知,梳理路径
(????)????????????????=????????+????(????>????,????,????∈?????);
(????)(????????)????=????????????(????>????,????,????∈?????);
(????)(????????)????=????????????????(????>????,????,????∈?????);
?
????????=????×????×????×??×????(????∈?????);
?
?????????=???? ????????(????∈?????);
?
(????)????????????????=????????+????(????>????,????,????∈????);
(????)(????????)????=????????????(????>????,????,????∈????);
(????)(????????)????=????????????????(????>????,????,????∈????);
?
问题3:谈到指数,在初中学习了正整数指数幂,你能说出正整数指数幂的意义和运算性质吗?
初中还把指数进行了扩充,使其可以取负整数,你能说出负整数指数幂意义是什么呢?
(二)复习旧知,梳理路径
问题4:在数系扩充的背景下,还想引进什么样的指数使指数幂进一步扩充?
自然数
负整数
整数
分数
有理数
无理数
实数
正整数指数幂
负整数整数指数幂
整数指数幂
分数指数幂
有理数指数幂
扩充的原则:
保持运算的协调性
运算性质的不变性
你认为扩充的原则是什么?
(三)类比学习,形成概念
????=±????
?
????=3????
?
如果????????=????,那么????叫做????的平方根(二次方根).记作 ;
?
如果????????=????,那么????叫做????的立方根(三次方根).记作 ;
?
比如:±????????=????,那么±????叫做4的平方根.
?
比如:?????????=?????,那么?????叫做?8的立方根.
?
问题5:在初中我们由平方、立方的运算,引入了平方根、立方根。你能举例说明它们的概念吗?
(三)类比学习,形成概念
如果 ,那么????叫做????的四次方根.记作 ;
?
????4=????
?
????=±4????
?
如果 ,那么????叫做????的五次方根.记作 ;
?
????5=????
?
????=5????
?
如果 ,那么????叫做????的????次方根.其中????>????,且????∈????? .
?
????????=????
?
追问1:类比二次方根、三次方根的定义,你能说出四次方根,五次方根的定义吗?
追问2:你能归纳出更一般的n次方根的定义吗?并举例说明.
比如:±????????=????????,那么±????叫做64的6次方根.
?
(三)类比学习,形成概念
如果 ,那么????叫做????的二次方根.记作 ;
?
如果 ,那么????叫做????的五次方根.记作 ;
?
如果 ,那么????叫做????的四次方根.记作 ;
?
如果 ,那么????叫做????的三次方根.记作 ;
?
????2=????
?
????=±????
?
????3=????
?
????=3????
?
????4=????
?
????5=????
?
????=±4????
?
????=5????
?
追问3:讨论任意实数????都有n次方根吗?有几个?该如何表示实数????的n次方根?可以举例说明.
?
如果 ,那么????叫做????的????次方根.其中????>????,且????∈????? .
?
????????=????
?
(三)类比学习,形成概念
分????为奇数与偶数
分????为正数、负数、零
?
????????叫做根式,
????叫做根指数,
????叫做被开方数
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
????为奇数
????为偶数
????>????
????????=????
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
存在,有一个,是正数????????
?
存在,有两个,是相反数±????????
?
存在,有一个,是负数????????
?
不存在
????????=????
?
比如:
10的5次方根是_______;
10的6次方根是________;
????(????>????)的6次方根是______;
????????(????>????)的7次方根是_____;
?
510
?
±610
?
±6????
?
7????2
?
(四)回归定义,发现性质
问题6:回顾二次根式的学习过程,我们先定义了二次根式,又探究了二次根式的性质(????)????=????,????????=????,那么n次根式有什么性质呢?
?
(四)回归定义,发现性质
????
?
????
?
????
?
?????
?
?????
?
问题6:回顾二次根式的学习过程,我们先定义了二次根式,又探究了二次根式的性质(????)????=????,????????=????,那么n次根式有什么性质呢?
?
(????????)????=????
?
追问:根据(????)????=????,你认为????次根式????????有什么类似性质?
?
(四)回归定义,感悟性质
追问:根据????????=????,你认为????次根式????????也有这样的性质吗?
?
????
?
????
?
????
?
????
?
????
?
?????
?
????
?
?????
?
根据运算中地不变性,得出
????????????=
?
计算下列根式的值?
????,????为奇数????,????为偶数
?
(五)深思熟虑,深化概念
例1.利用????次方根的性质,计算下列值
?
追问:观察????????????????=????????,2与5,10之间有什么关系?
????????????????=????????,3与4,12之间有什么关系?
?
当根式的被开方数的指数能被根指数整除时,
根式可以表示为分数指数幂的形式.
5????25=????2
?
4????34=??3
?
=????????????????
?
由此你能得出什么结论?
=????????????????
?
=????????????×????????
?
=????????????????????
?
=????????????×????????=????????????????????
?
(五)深思熟虑,深化概念
问题7:当根式的被开方数的指数不能被根指数整除时,根式是否也可以表示为分数指数幂的形式?
????????????
?
????????????
?
????????????
?
????????????
?
????????????
?
????????=????
?
= ? ????
?
指数幂的运算性质不发生变化
????????????=????=(???????? ????)????
?
????????????=????=(????????????)????
?
????????????????=????????=(???????? ????)????
?
????????????????=????????=(???????? ????)????
?
(五)深思熟虑,深化概念
?????????????=_________ (????>??,????,????∈?????,????>????)
?
1????????????
?
0的正分数指数幂等于0,0负分数指数幂不存在
追问1:类比?????????=????????????(????∈????,????≠????),你能得到负分数指数幂的定义吗?
?
追问2:0的正分数指数幂等于几?0有负分数指数幂吗?
规定:正数的正分数指数幂????????????=_________ (????>????,????,????∈?????,????>????)
?
????????????
?
整数指数幂的运算性质确实对有理数指数幂的运算适用,我们用计算机来加以验证.
(????)????????????????=????????+????(????>????,????,????∈????);
(????)(????????)????=????????????(????>????,????,????∈????);
(????)(????????)????=????????????????(????>????,????,????∈????);
?
(五)深思熟虑,深化概念
有理数指数幂的其他性质(????>????,????∈????)
?
1.若????>????时,????????随????的增大而增大.
?
2.若?????
(六)巩固知识,典例应用
例2.求值
(六)巩固知识,典例应用
例3.用分数指数幂的形式表示并计算下列各式(其中????>????)
?
(七)归纳总结,强化思想
1.回顾本节的内容和学习过程谈谈你的收获?
n次方根
定义
表示
性质
根式
整数指数幂
有理数指数幂
分数指数幂
二次方根
三次方根
……
(七)归纳总结,强化思想
2.在数系扩充的背景下,你还希望将指数的范围如何扩充?扩充的原则是什么?
实数
有理数
整数
自然数
?
有理数指数幂
整数指数幂
正整数指数幂
(八)强化训练,布置作业
1.基础性作业
P107页1,2,3
P109页1,4
2.探究性作业
P110页拓广探索10题
3.课前任务
估算????的值
?
感谢聆听
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
