九年级数学北师大版上册 《6.2反比例函数的图像与性质》 同步学案(无答案)
文档属性
| 名称 | 九年级数学北师大版上册 《6.2反比例函数的图像与性质》 同步学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 403.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-19 22:01:41 | ||
图片预览


文档简介
反比例函数的图象与性质
【学习目标】
1.能描点画出反比例函数的图象。
2.根据反比例函数的图象和解析式,探索并理解其性质。
【学习重难点】
根据反比例函数的图象和解析式,探索并理解其性质。
【学习过程】
一、知识回顾
1.下列哪些等式中的y是x的反比例函数?若是,请指出系数k 的值
(1) (2) (3)xy=21 (4)
(5) (6) (7)y=x-4 (8)
2.已知y与x成反比例,且当x=-2时,y=3,则y与x之间的函数关系式是 ,当x=-3时,y=
3.函数的图象是________,它经过第_________象限,函数值y随x的增大而_____;函数的图象是_________,它经过第_________象限,函数值y随x的增大而_____
二、学习新知
知识要点一:反比例函数的图象和性质
1.探索活动:
(1)请用描点法画出函数和的图象
分析:由于反比例函数和,自变量的取值范围是_______________
因此,列表取值时,自变量可取 ,并求出对应的函数值
x … …
… …
… …
描点、连线:
(2)请用描点法画出函数和的图象
列表:
x … …
… …
… …
描点、连线:
观察图象,归纳性质:
函数 反比例函数
k 的符号 k>0 k<0
图象
经过象限 图象经过第______象限 图象经过第______象限
性质 在每一象限内,y随x的增大而___________ 在每一象限内,y随x的增大而___________
知识要点二:反比例函数性质的运用
例1.已知反比例函数的图象经过点A(2,6)
(1)这个函数的图象位于第几象限?y随x的增大如何变化?
(2)点B(3,4),C(2,5),D(,)、E(-2,-6)是否在这个函数图象上?
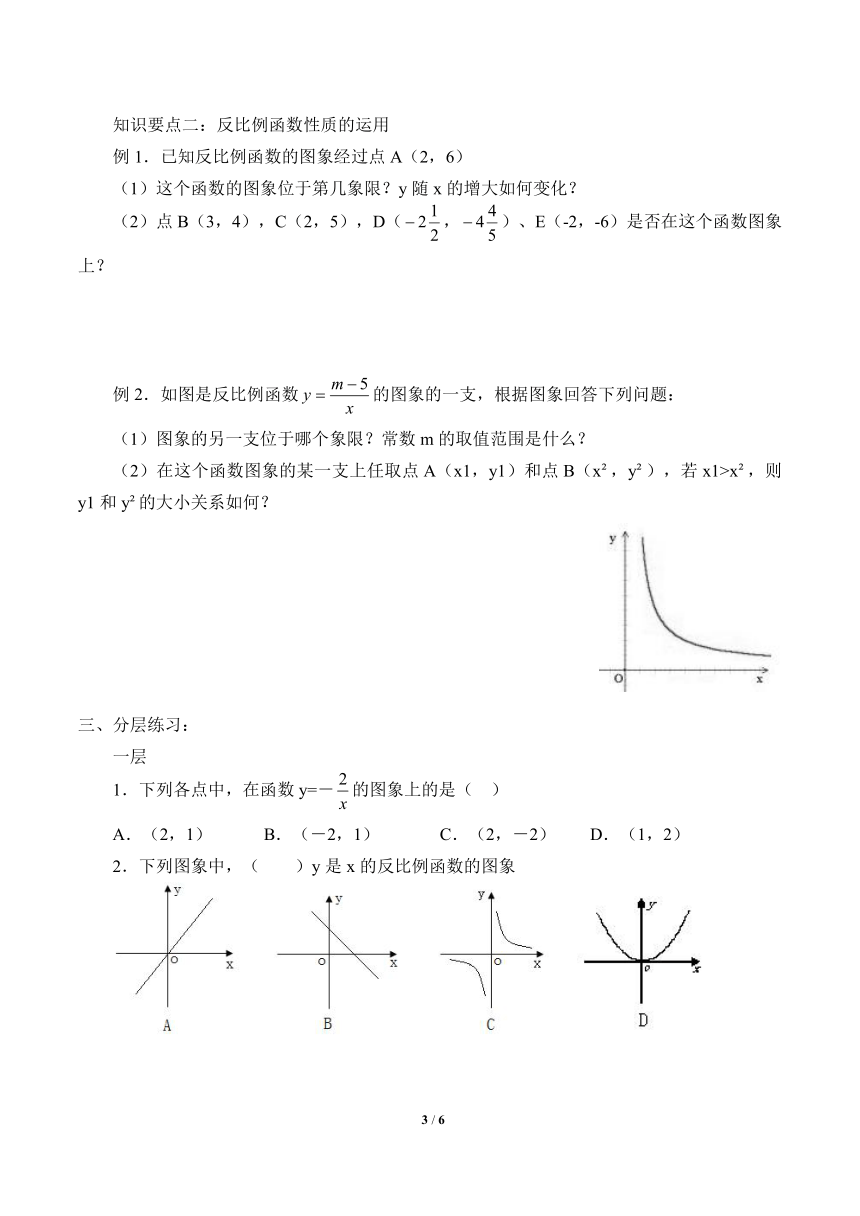
例2.如图是反比例函数的图象的一支,根据图象回答下列问题:
(1)图象的另一支位于哪个象限?常数m的取值范围是什么?
(2)在这个函数图象的某一支上任取点A(x1,y1)和点B(x ,y ),若x1>x ,则y1和y 的大小关系如何?
三、分层练习:
一层
1.下列各点中,在函数y=-的图象上的是( )
A.(2,1) B.(-2,1) C.(2,-2) D.(1,2)
2.下列图象中,( )y是x的反比例函数的图象
3.如图为某函数的图象,这个函数的解析式是( )
A. B.
C. D.
4.反比例函数的图象位于第 象限,在每个象限内y随x的增大而 。
二层:
5.反比例函数y=的图象经过点(―2,―3),那么函数的图象应该位于( )
A.第一、三象限 B.第一、二象限 C.第二、四象限 D.第三、四象限
6.(1)若反比例函数y=的图象如图所示,则k的取值范围是___________
(2)若反比例函数y=在每个象限内,y随x的增大而增大,则k的取值范围是___________。
7.若点(-2,y1)、(-1,y )都在反比例函数y=-的图像上,则y1.y 的大小关系是
_。
三层:
8.(1)已知,在同一平面直角坐标系中,函数与的图象大致是( )
(2)已知,在同一平面直角坐标系中,函数与的图象大致是( )
9.若点(x1,y1)、(x ,y )(x ,y )都在反比例函数y=的图像上,且x1< x <0< x ,则y1.y 和y 的大小关系是________________
四、小结
函数 反比例函数 正比例函数
k 的符号 k>0 k<0 k>0 k<0
图象
性质
【达标检测】
一、必做题
1.(1)已知反比例函数的图象如图所示,则k______0,在图象的每一支上,y随x的增大而________
(2)已知反比例函数的图象如图所示,则k______0,在图象的每一支上,y随x的增大而________
2.已知函数的图象经过点(—1,3),若点(2,m)在这个图象上,则m=___________
3.老师给出了一个函数,甲、乙、丙三位同学分别指出了它的一个性质:甲:第一象限内有它的图象;乙:第三象限内有它的图象;丙:在每一个象限内,y随x的增大而减少。请你写出一个满足以上条件的函数解析式:________ ___
4.(1)画出反比例函数的图象
(2)求当-4 < x < -1时,反比例函数y的范围。
5.已知反比例函数的图象经过(m,—m),那么它的图象在第_________象限
6.已知反比例函数的图象经过点(-3,-12),且双曲线位于第二、四象限,则函数的图象必定不经过第_________象限
7.已知点(a,b)是反比例函数的图象上的任一点,则下列各点中,不一定在这个函数的图象上的是( )
A.(-a,-b) B.(b,a) C.(-b,-a) D.(,)
8.已知点A(0,2)和点B(0,-2),点P在函数的图象上,若△PAB的面积为6,求点P的坐标。
6 / 6
【学习目标】
1.能描点画出反比例函数的图象。
2.根据反比例函数的图象和解析式,探索并理解其性质。
【学习重难点】
根据反比例函数的图象和解析式,探索并理解其性质。
【学习过程】
一、知识回顾
1.下列哪些等式中的y是x的反比例函数?若是,请指出系数k 的值
(1) (2) (3)xy=21 (4)
(5) (6) (7)y=x-4 (8)
2.已知y与x成反比例,且当x=-2时,y=3,则y与x之间的函数关系式是 ,当x=-3时,y=
3.函数的图象是________,它经过第_________象限,函数值y随x的增大而_____;函数的图象是_________,它经过第_________象限,函数值y随x的增大而_____
二、学习新知
知识要点一:反比例函数的图象和性质
1.探索活动:
(1)请用描点法画出函数和的图象
分析:由于反比例函数和,自变量的取值范围是_______________
因此,列表取值时,自变量可取 ,并求出对应的函数值
x … …
… …
… …
描点、连线:
(2)请用描点法画出函数和的图象
列表:
x … …
… …
… …
描点、连线:
观察图象,归纳性质:
函数 反比例函数
k 的符号 k>0 k<0
图象
经过象限 图象经过第______象限 图象经过第______象限
性质 在每一象限内,y随x的增大而___________ 在每一象限内,y随x的增大而___________
知识要点二:反比例函数性质的运用
例1.已知反比例函数的图象经过点A(2,6)
(1)这个函数的图象位于第几象限?y随x的增大如何变化?
(2)点B(3,4),C(2,5),D(,)、E(-2,-6)是否在这个函数图象上?
例2.如图是反比例函数的图象的一支,根据图象回答下列问题:
(1)图象的另一支位于哪个象限?常数m的取值范围是什么?
(2)在这个函数图象的某一支上任取点A(x1,y1)和点B(x ,y ),若x1>x ,则y1和y 的大小关系如何?
三、分层练习:
一层
1.下列各点中,在函数y=-的图象上的是( )
A.(2,1) B.(-2,1) C.(2,-2) D.(1,2)
2.下列图象中,( )y是x的反比例函数的图象
3.如图为某函数的图象,这个函数的解析式是( )
A. B.
C. D.
4.反比例函数的图象位于第 象限,在每个象限内y随x的增大而 。
二层:
5.反比例函数y=的图象经过点(―2,―3),那么函数的图象应该位于( )
A.第一、三象限 B.第一、二象限 C.第二、四象限 D.第三、四象限
6.(1)若反比例函数y=的图象如图所示,则k的取值范围是___________
(2)若反比例函数y=在每个象限内,y随x的增大而增大,则k的取值范围是___________。
7.若点(-2,y1)、(-1,y )都在反比例函数y=-的图像上,则y1.y 的大小关系是
_。
三层:
8.(1)已知,在同一平面直角坐标系中,函数与的图象大致是( )
(2)已知,在同一平面直角坐标系中,函数与的图象大致是( )
9.若点(x1,y1)、(x ,y )(x ,y )都在反比例函数y=的图像上,且x1< x <0< x ,则y1.y 和y 的大小关系是________________
四、小结
函数 反比例函数 正比例函数
k 的符号 k>0 k<0 k>0 k<0
图象
性质
【达标检测】
一、必做题
1.(1)已知反比例函数的图象如图所示,则k______0,在图象的每一支上,y随x的增大而________
(2)已知反比例函数的图象如图所示,则k______0,在图象的每一支上,y随x的增大而________
2.已知函数的图象经过点(—1,3),若点(2,m)在这个图象上,则m=___________
3.老师给出了一个函数,甲、乙、丙三位同学分别指出了它的一个性质:甲:第一象限内有它的图象;乙:第三象限内有它的图象;丙:在每一个象限内,y随x的增大而减少。请你写出一个满足以上条件的函数解析式:________ ___
4.(1)画出反比例函数的图象
(2)求当-4 < x < -1时,反比例函数y的范围。
5.已知反比例函数的图象经过(m,—m),那么它的图象在第_________象限
6.已知反比例函数的图象经过点(-3,-12),且双曲线位于第二、四象限,则函数的图象必定不经过第_________象限
7.已知点(a,b)是反比例函数的图象上的任一点,则下列各点中,不一定在这个函数的图象上的是( )
A.(-a,-b) B.(b,a) C.(-b,-a) D.(,)
8.已知点A(0,2)和点B(0,-2),点P在函数的图象上,若△PAB的面积为6,求点P的坐标。
6 / 6
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
