九年级数学北师大版上册 《6.2反比例函数的图像与性质》 学案 (无答案)
文档属性
| 名称 | 九年级数学北师大版上册 《6.2反比例函数的图像与性质》 学案 (无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 372.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-20 07:58:58 | ||
图片预览

文档简介
反比例函数的图象与性质
【学习目标】
1.进一步熟悉画函数图像的主要步骤会画反比例函数图像;
2.体会函数三种表示方式的相互转换,对函数进行认识上的审核;
3.理解反比例函数的性质。
【学习过程】
一、自主学习:
1.若ab < 0,则函数y = ax与y = 在同一平面直角坐标系中的图象大致是( )
2.如图是三个反比例函数y = ,y = ,y = ,在x轴的上方
的图象,由此观察得到k1.k2.k3的大小关系为( )
A. k1 > k2 > k3 B. k2 > k3 > k1 C. k3 > k2 > k1 D. k3 > k1 > k2
3.已知点P、Q在反比函数y =的图象上。
(1)若P(1,a),Q (2,b), 比较a.b的大小;
(2)若P( 1,a),Q( 2,b),比较a.b的大小;
(3)你能从中发现y随x增大时的变化规律吗?
(4)若P(x1,y1),Q(x2,y2),x1二、小组交流,合作探究
反比例函数的图象是由 组成的。(通常称为 )
当>时,两支曲线分别位于第 象限内,在每一象限内,的值
当<时,两支曲线分别位于第 象限内,在每一象限内,的值
三、全班交流,例题学习
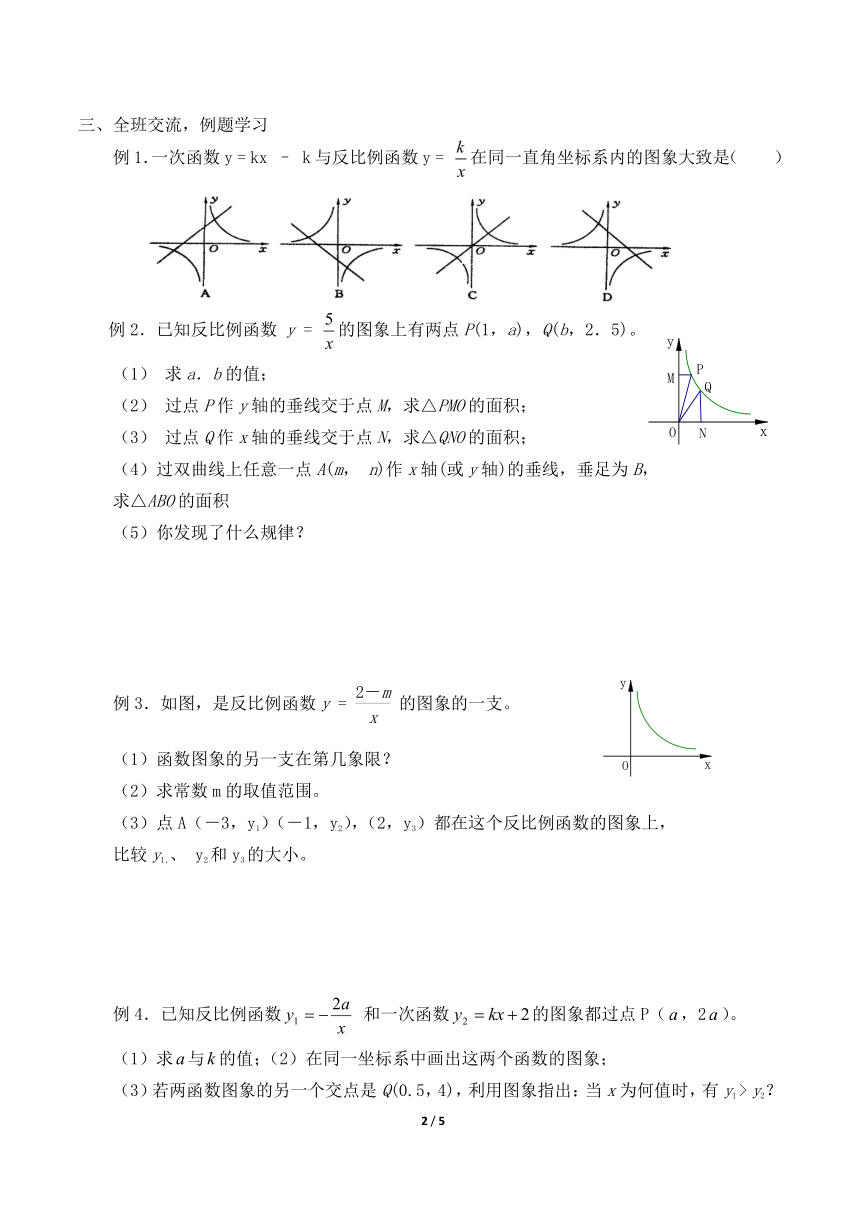
例1.一次函数y = kx – k与反比例函数y = 在同一直角坐标系内的图象大致是( )
例2.已知反比例函数 y = 的图象上有两点P(1,a),Q(b,2.5)。
(1) 求a.b的值;
(2) 过点P作y轴的垂线交于点M,求△PMO的面积;
(3) 过点Q作x轴的垂线交于点N,求△QNO的面积;
(4)过双曲线上任意一点A(m, n)作x轴(或y轴)的垂线,垂足为B,
求△ABO的面积
(5)你发现了什么规律?
例3.如图,是反比例函数y = 的图象的一支。
(1)函数图象的另一支在第几象限?
(2)求常数m的取值范围。
(3)点A(-3,y1)(-1,y2),(2,y3)都在这个反比例函数的图象上,
比较y1.、 y2和y3的大小。
例4.已知反比例函数 和一次函数的图象都过点P(,2)。
(1)求与的值;(2)在同一坐标系中画出这两个函数的图象;
(3)若两函数图象的另一个交点是Q(0.5,4),利用图象指出:当x为何值时,有y1 > y2?
【达标检测】
1.已知反比例函数的图象在第二、四象限内,函数图象上有两点,,则与的大小关系为( )
A. B. C. D.无法确定
2.已知一次函数y=kx+b的图象经过第二、三、四象限,则反比例函数 的图象在( )
A.第一、二象限; B.第三、四象限; C.第一、三象限; D.第二、四象限。
3.若反比例函数y=的图象经过第二、四象限,则函数的解析式为 。
4.已知反比例函数的图像与一次函数y=kx+m的图像相交于点A(2,1)。
(1)分别求出这两个函数的解析式;
(2)当x取什么范围时,反比例函数值大于0;
(3)若一次函数与反比例函数另一交点为B,且纵坐标为-4,当x取什么范围时,反比例函数值大于一次函数的值;
(4)试判断点P(—1,5)关于x轴的对称点P‘是否在一次函数y=kx+m的图像上。
【作业布置】
一、选择题
1.已知函数,则其图象在平面直角坐标系中可能是( )
2.如图1,A.B是函数的图象上关于原点对称的任意两点,BC∥轴,AC∥轴,△ABC的面积记为,则( )
A. B. C. D.
3. (知识点1)如图2,在直角坐标系中,点是轴正半轴上的一个定点,点是双曲线()上的一个动点,当点的横坐标逐渐增大时,的面积将会 ( )
A.逐渐增大 B.不变 C.逐渐减小 D.先增大后减小
二、填空题:
1.如图3,直线l与双曲线交于A.C两点,将直线l绕点O顺时针旋转度角(0°<≤45°),与双曲线交于B.D两点,则四边形ABCD的形状一定是_______________形。
三、解答题:
1.点(-2,)、(-1,)、(1,)在反比例函数 = (k < 0)的图象上,比较、、的大小。
2.已知反比例函数 =与一次函数= mx + b的图象交于P(-2,1)和Q(1,n)两点。
(1)求反比例函数的解析式;(2)求n的值;(3)求一次函数 = mx + b的解析式。
3.正比例函数 = 2x的图象与反比例函数=的图象有一个交点的横坐标是3,
(1)求k的值;
(2)根据反比例函数的图象,当-3 < x < -1时,求的取值范围;
(3)当-3 < < -1时,求x的取值范围;
(4)当0 < x < 3时, > ;当x > 3时,0 < < ,即是小于 的正数;当x > 时,是小于1的正数。
(5)当x为何值时,> ? 当x为何值时,<?
选做题:
4.已知一次函数= kx + b (k ≠ 0)的图象与x轴、轴交于A.B两点,且与反比例函数= (m ≠ 0)的图象在第一象限交于点C,CD⊥x轴于D,且OA = OB = OD =1。
(1)求点A、B、D的坐标;
(2)求一次函数和反比例函数的解析式。
5 / 5
【学习目标】
1.进一步熟悉画函数图像的主要步骤会画反比例函数图像;
2.体会函数三种表示方式的相互转换,对函数进行认识上的审核;
3.理解反比例函数的性质。
【学习过程】
一、自主学习:
1.若ab < 0,则函数y = ax与y = 在同一平面直角坐标系中的图象大致是( )
2.如图是三个反比例函数y = ,y = ,y = ,在x轴的上方
的图象,由此观察得到k1.k2.k3的大小关系为( )
A. k1 > k2 > k3 B. k2 > k3 > k1 C. k3 > k2 > k1 D. k3 > k1 > k2
3.已知点P、Q在反比函数y =的图象上。
(1)若P(1,a),Q (2,b), 比较a.b的大小;
(2)若P( 1,a),Q( 2,b),比较a.b的大小;
(3)你能从中发现y随x增大时的变化规律吗?
(4)若P(x1,y1),Q(x2,y2),x1
反比例函数的图象是由 组成的。(通常称为 )
当>时,两支曲线分别位于第 象限内,在每一象限内,的值
当<时,两支曲线分别位于第 象限内,在每一象限内,的值
三、全班交流,例题学习
例1.一次函数y = kx – k与反比例函数y = 在同一直角坐标系内的图象大致是( )
例2.已知反比例函数 y = 的图象上有两点P(1,a),Q(b,2.5)。
(1) 求a.b的值;
(2) 过点P作y轴的垂线交于点M,求△PMO的面积;
(3) 过点Q作x轴的垂线交于点N,求△QNO的面积;
(4)过双曲线上任意一点A(m, n)作x轴(或y轴)的垂线,垂足为B,
求△ABO的面积
(5)你发现了什么规律?
例3.如图,是反比例函数y = 的图象的一支。
(1)函数图象的另一支在第几象限?
(2)求常数m的取值范围。
(3)点A(-3,y1)(-1,y2),(2,y3)都在这个反比例函数的图象上,
比较y1.、 y2和y3的大小。
例4.已知反比例函数 和一次函数的图象都过点P(,2)。
(1)求与的值;(2)在同一坐标系中画出这两个函数的图象;
(3)若两函数图象的另一个交点是Q(0.5,4),利用图象指出:当x为何值时,有y1 > y2?
【达标检测】
1.已知反比例函数的图象在第二、四象限内,函数图象上有两点,,则与的大小关系为( )
A. B. C. D.无法确定
2.已知一次函数y=kx+b的图象经过第二、三、四象限,则反比例函数 的图象在( )
A.第一、二象限; B.第三、四象限; C.第一、三象限; D.第二、四象限。
3.若反比例函数y=的图象经过第二、四象限,则函数的解析式为 。
4.已知反比例函数的图像与一次函数y=kx+m的图像相交于点A(2,1)。
(1)分别求出这两个函数的解析式;
(2)当x取什么范围时,反比例函数值大于0;
(3)若一次函数与反比例函数另一交点为B,且纵坐标为-4,当x取什么范围时,反比例函数值大于一次函数的值;
(4)试判断点P(—1,5)关于x轴的对称点P‘是否在一次函数y=kx+m的图像上。
【作业布置】
一、选择题
1.已知函数,则其图象在平面直角坐标系中可能是( )
2.如图1,A.B是函数的图象上关于原点对称的任意两点,BC∥轴,AC∥轴,△ABC的面积记为,则( )
A. B. C. D.
3. (知识点1)如图2,在直角坐标系中,点是轴正半轴上的一个定点,点是双曲线()上的一个动点,当点的横坐标逐渐增大时,的面积将会 ( )
A.逐渐增大 B.不变 C.逐渐减小 D.先增大后减小
二、填空题:
1.如图3,直线l与双曲线交于A.C两点,将直线l绕点O顺时针旋转度角(0°<≤45°),与双曲线交于B.D两点,则四边形ABCD的形状一定是_______________形。
三、解答题:
1.点(-2,)、(-1,)、(1,)在反比例函数 = (k < 0)的图象上,比较、、的大小。
2.已知反比例函数 =与一次函数= mx + b的图象交于P(-2,1)和Q(1,n)两点。
(1)求反比例函数的解析式;(2)求n的值;(3)求一次函数 = mx + b的解析式。
3.正比例函数 = 2x的图象与反比例函数=的图象有一个交点的横坐标是3,
(1)求k的值;
(2)根据反比例函数的图象,当-3 < x < -1时,求的取值范围;
(3)当-3 < < -1时,求x的取值范围;
(4)当0 < x < 3时, > ;当x > 3时,0 < < ,即是小于 的正数;当x > 时,是小于1的正数。
(5)当x为何值时,> ? 当x为何值时,<?
选做题:
4.已知一次函数= kx + b (k ≠ 0)的图象与x轴、轴交于A.B两点,且与反比例函数= (m ≠ 0)的图象在第一象限交于点C,CD⊥x轴于D,且OA = OB = OD =1。
(1)求点A、B、D的坐标;
(2)求一次函数和反比例函数的解析式。
5 / 5
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
