湘教版八年级上册5.3.2 二次根式的加法和减法 课件(共27张PPT)
文档属性
| 名称 | 湘教版八年级上册5.3.2 二次根式的加法和减法 课件(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-20 08:30:58 | ||
图片预览








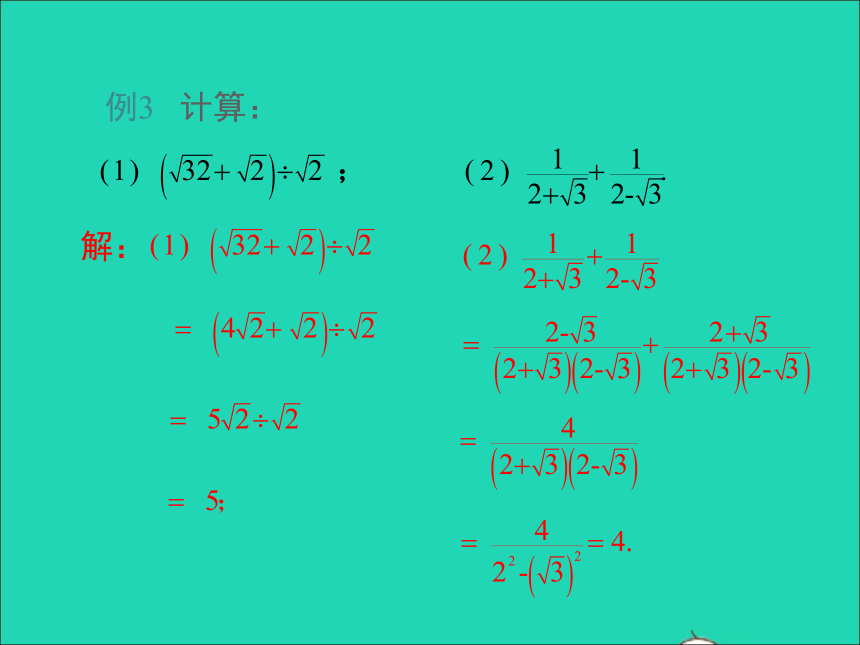
文档简介
(共27张PPT)
第5章
二次根式
5.3二次根式的加法和减法
第2课时
1.掌握二次根式的混合运算及其应用;(重点、难点)
2.掌握乘法公式在二次根式混合运算中的作用.
学习目标
导入新课
问题1 单项式与多项式、多项式与多项式的乘法法则法则分别是什么
问题2 多项式与单项式的除法法则是什么
m(a+b+c)=ma+mb+mc;
(m+n)(a+b)=ma+mb+na+nb
复习引入
(ma+mb+mc)÷m=a+b+c
分配律
单×多
转化
前面两个问题的思路是:
思考 若把字母a,b,c,m都用二次根式代替(每个同学任选一组),然后对比归纳,你们发现了什么?
单×单
二次根式的加、减、乘、除混合运算与整式运算一样,体现在:运算律、运算顺序、乘法法则仍然适用.
引例:甲、乙两个城市间计划修建一条城际铁路, 其中有一段路基的横断面设计为上底宽 ,下底宽 ,高 的梯形,这段路基长 500 m,那么这段路基的土石方 (路基的土石方即等于路基的体积)为多少立方米呢?
讲授新课
二次根式的混合运算
解:路基的土石方等于路基横断面面积乘以路基的长度,所以,这段路基的土石方为:
答:这段路基的土石方为
从上面的解答过程可以看到,二次根式的混合运算是根据实数的运算律进行的.
例1 计算:
例2 计算:
利用平方差公式展开
利用完全平方公式展开
例3 计算:
解:
解法一:
(3)
你还有其他解法吗?
计算:
试一试
解法二: 原式=
二次根式的混合运算,一般先将二次根式转化为最简二次根式,再灵活运用乘法公式等知识来简化计算.
要点归纳
例4 已知 试求x2+2xy+y2的值.
解: x2+2xy+y2=(x+y)2
把 代入上式得
原式=
二次根式的应用
解:∵ ,
∴
∴x3y+xy3=xy(x2+y2)=xy[(x+y)2-2xy]
【变式题】 已知 ,求x3y+xy3.
用整体代入法求代数式值的方法:求关于x,y的对称式(即交换任意两个字母的位置后,代数式不变)的值,一般先求x+y,xy,x-y, 等的值,然后将所求代数式适当变形成知含x+y,xy,x-y, 等式子,再代入求值.
归纳
在前面我们学习了二次根式的除法法则时,学会了怎样去掉分母的二次根式的方法,比如:
拓展探究
思考 如果分母不是单个的二次根式,而是含二次根式的式子,如: 等,该怎样去掉分母中的二次根式呢?
根据整式的乘法公式在二次根式中也适用,你能想到什么好方法吗?
例5 计算:
解:
分母形如 的式子,分子、分母同乘以 的式子,构成平方差公式,可以使分母不含根号.
归纳
【变式题】 已知 ,求 .
解:∵
解决二次根式的化简求值问题时,先化简已知条件,再用乘法公式变形、代入求值即可.
归纳
已知 的整数部分是a,小数部分是b,求a2-b2的值.
解:
练一练
例6:教师节就要到了,李欣同学准备做两张大小不同的正方形贺卡送给老师以表示祝贺,其中一张面积为288平方厘米,另一张面积为338平方厘米.如果用彩带把贺卡镶边会更漂亮,她现在有1.5米的彩带,请你帮忙算一算她的彩带够不够用.
分析:可以通过两个正方形的面积分别计算出正方形的边长,进一步求出两个正方形的周长之和,与1.5米比较即可得出结论.
解:贺卡的周长为
答:李欣的彩带够用.
本题是利用二次根式的加法来解决实际生活中的问题,解答本题的关键在于理解题意并列出算式.
方法总结
当堂练习
1.下列计算中正确的是( )
B
2.已知 试求x2+2xy+y2的值.
解: x2+2xy+y2=(x+y)2
把 代入上式得
原式=
(1) ;
(2) ;
(3) .
解:
(1)
(2)
3.计算.
解:
(3)
=10 .
4.在一个边长为 cm的正方形内部,挖去一个边长为 cm的正方形,求剩余部分的面积.
解:由题意得,
即剩余部分的面积是
5.阅读下列材料,然后回答问题:
在进行类似于二次根式 的运算时,通常有如下两种方法将其进一步化简:
方法一:
方法二:
能力提升:
(1)请用两种不同的方法化简:
(2)化简:
解:(1)
二次根式的运算
乘除法则
课堂小结
加减法则
乘除公式
第5章
二次根式
5.3二次根式的加法和减法
第2课时
1.掌握二次根式的混合运算及其应用;(重点、难点)
2.掌握乘法公式在二次根式混合运算中的作用.
学习目标
导入新课
问题1 单项式与多项式、多项式与多项式的乘法法则法则分别是什么
问题2 多项式与单项式的除法法则是什么
m(a+b+c)=ma+mb+mc;
(m+n)(a+b)=ma+mb+na+nb
复习引入
(ma+mb+mc)÷m=a+b+c
分配律
单×多
转化
前面两个问题的思路是:
思考 若把字母a,b,c,m都用二次根式代替(每个同学任选一组),然后对比归纳,你们发现了什么?
单×单
二次根式的加、减、乘、除混合运算与整式运算一样,体现在:运算律、运算顺序、乘法法则仍然适用.
引例:甲、乙两个城市间计划修建一条城际铁路, 其中有一段路基的横断面设计为上底宽 ,下底宽 ,高 的梯形,这段路基长 500 m,那么这段路基的土石方 (路基的土石方即等于路基的体积)为多少立方米呢?
讲授新课
二次根式的混合运算
解:路基的土石方等于路基横断面面积乘以路基的长度,所以,这段路基的土石方为:
答:这段路基的土石方为
从上面的解答过程可以看到,二次根式的混合运算是根据实数的运算律进行的.
例1 计算:
例2 计算:
利用平方差公式展开
利用完全平方公式展开
例3 计算:
解:
解法一:
(3)
你还有其他解法吗?
计算:
试一试
解法二: 原式=
二次根式的混合运算,一般先将二次根式转化为最简二次根式,再灵活运用乘法公式等知识来简化计算.
要点归纳
例4 已知 试求x2+2xy+y2的值.
解: x2+2xy+y2=(x+y)2
把 代入上式得
原式=
二次根式的应用
解:∵ ,
∴
∴x3y+xy3=xy(x2+y2)=xy[(x+y)2-2xy]
【变式题】 已知 ,求x3y+xy3.
用整体代入法求代数式值的方法:求关于x,y的对称式(即交换任意两个字母的位置后,代数式不变)的值,一般先求x+y,xy,x-y, 等的值,然后将所求代数式适当变形成知含x+y,xy,x-y, 等式子,再代入求值.
归纳
在前面我们学习了二次根式的除法法则时,学会了怎样去掉分母的二次根式的方法,比如:
拓展探究
思考 如果分母不是单个的二次根式,而是含二次根式的式子,如: 等,该怎样去掉分母中的二次根式呢?
根据整式的乘法公式在二次根式中也适用,你能想到什么好方法吗?
例5 计算:
解:
分母形如 的式子,分子、分母同乘以 的式子,构成平方差公式,可以使分母不含根号.
归纳
【变式题】 已知 ,求 .
解:∵
解决二次根式的化简求值问题时,先化简已知条件,再用乘法公式变形、代入求值即可.
归纳
已知 的整数部分是a,小数部分是b,求a2-b2的值.
解:
练一练
例6:教师节就要到了,李欣同学准备做两张大小不同的正方形贺卡送给老师以表示祝贺,其中一张面积为288平方厘米,另一张面积为338平方厘米.如果用彩带把贺卡镶边会更漂亮,她现在有1.5米的彩带,请你帮忙算一算她的彩带够不够用.
分析:可以通过两个正方形的面积分别计算出正方形的边长,进一步求出两个正方形的周长之和,与1.5米比较即可得出结论.
解:贺卡的周长为
答:李欣的彩带够用.
本题是利用二次根式的加法来解决实际生活中的问题,解答本题的关键在于理解题意并列出算式.
方法总结
当堂练习
1.下列计算中正确的是( )
B
2.已知 试求x2+2xy+y2的值.
解: x2+2xy+y2=(x+y)2
把 代入上式得
原式=
(1) ;
(2) ;
(3) .
解:
(1)
(2)
3.计算.
解:
(3)
=10 .
4.在一个边长为 cm的正方形内部,挖去一个边长为 cm的正方形,求剩余部分的面积.
解:由题意得,
即剩余部分的面积是
5.阅读下列材料,然后回答问题:
在进行类似于二次根式 的运算时,通常有如下两种方法将其进一步化简:
方法一:
方法二:
能力提升:
(1)请用两种不同的方法化简:
(2)化简:
解:(1)
二次根式的运算
乘除法则
课堂小结
加减法则
乘除公式
同课章节目录
