勾股定理(1)[下学期]
文档属性
| 名称 | 勾股定理(1)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 610.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-08 19:08:00 | ||
图片预览






文档简介
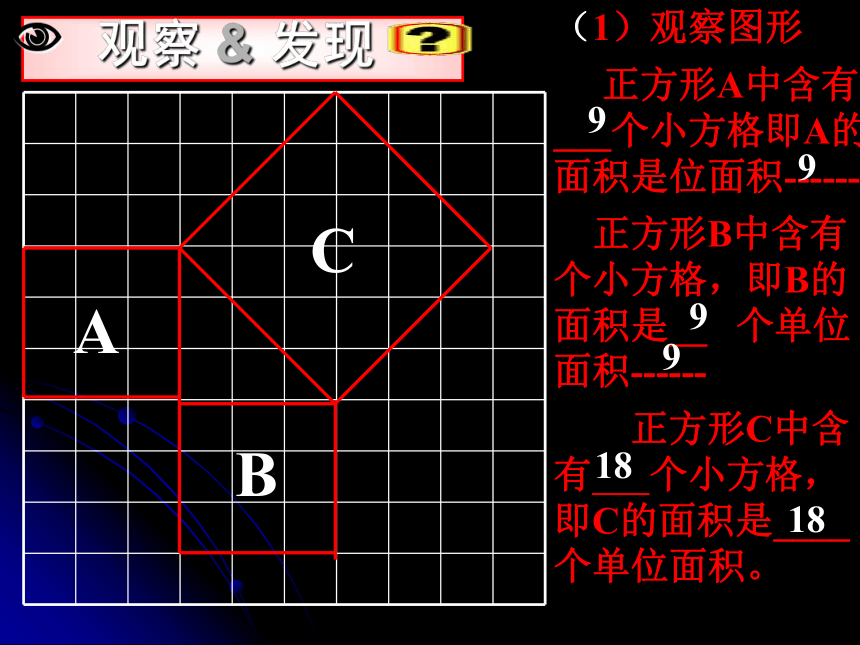
课件22张PPT。18.1.1 勾股定理2002年,在北京举行的国际数学家大会会标讲故事同学们,我们也来观察图中的地面,看看你能发现什么?是否和大哲学家有同样的发现呢?你能发现图中的等腰直角三角形有什么性质吗?(1)观察图形
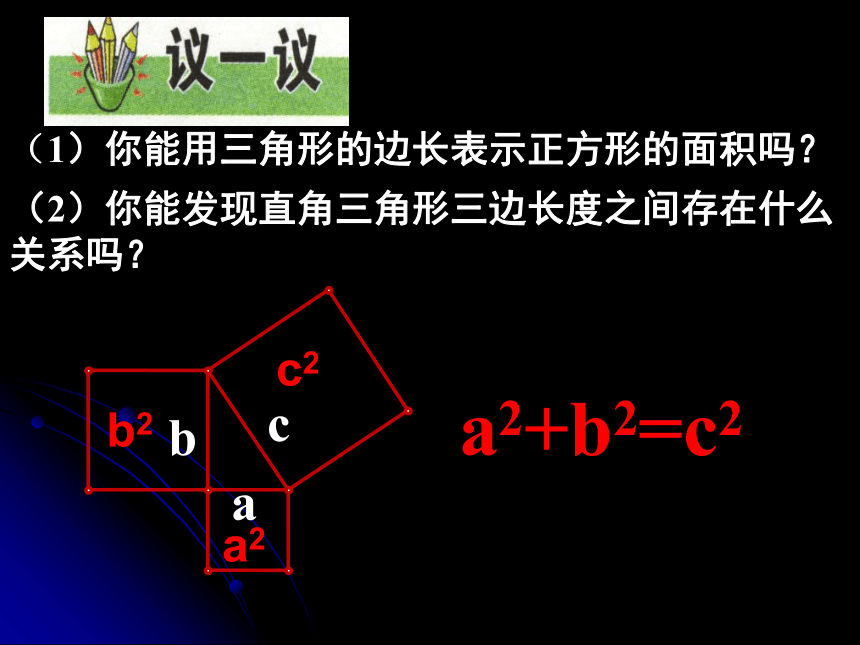
正方形A中含有 ___个小方格即A的面积是位面积------
正方形B中含有 个小方格,即B的面积是__ 个单位面积------
正方形C中含有 个小方格,即C的面积是____个单位面积。 99181899CAB(1)你能用三角形的边长表示正方形的面积吗?
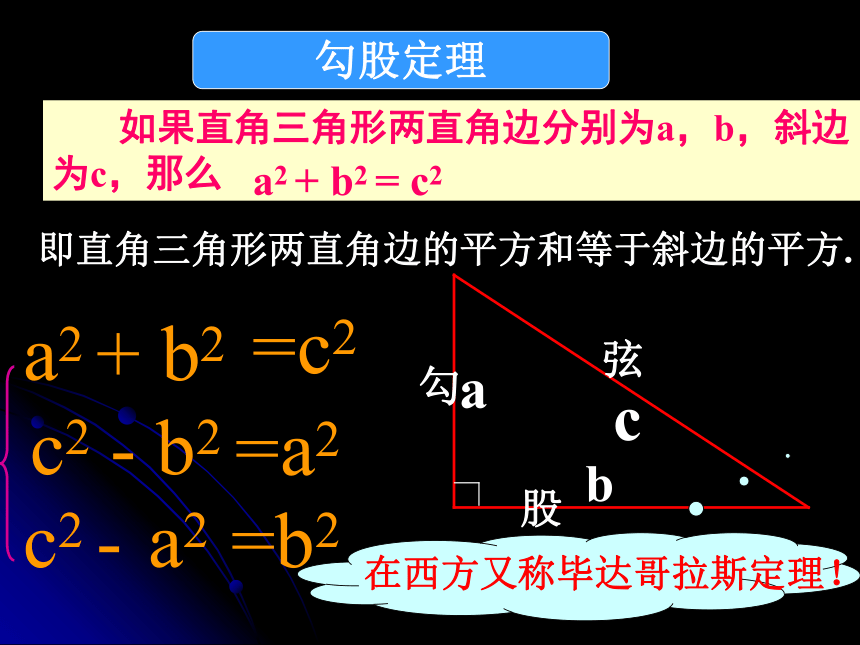
(2)你能发现直角三角形三边长度之间存在什么关系吗?baca2+b2=c2c2a2b2在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”. 如果直角三角形两直角边分别为a,b,斜边为c,那么a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方.勾股定理在西方又称毕达哥拉斯定理!a2 + b2c2 - b2c2 - a2=c2 =a2=b2 证法(一) 有人利用这4个直角三角形拼出了右图,你能用两种方法表示大正方形的面积吗?大正方形的面积可以表示为 —————————— 又可以表示为:———————对比两种表示方法,你得到勾股定理了吗?(a+b)2验证勾股定理:证法(二) 弦图赵爽
东汉末至三国时代吴国人
为《周髀算经》作注,并著有《勾股圆方图说》。cb ? a c2 = (b ?a)2 +
= a2 ? 2ab + b2 + 2abab? c2= a2 + b2 ?(a + b)(b + a) = ?c2 + 2(?ab)
?a2 + ab + ?b2 = ?c2 + ab
? a2 + b2 = c2aabbcc伽菲尔德的证明方法.1881年,伽菲尔德就任美国第二十任总统后,人们为了纪念他对勾股定理的证明,就称这一证法称为“总统”证法。
∟∟∟证法(三)
总统证法 你还有其他证明方法吗? 例 1.在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.例题分析(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.方法小结例2:如图将长为5.41米的梯子AC斜靠在墙上,BC长
为2.16米,求梯子上端A到墙的底端B的距离AB(精确
到0.01米)分析:先把实际问题转化成数学问题。求:AB的长。解:在Rt⊿ABC中,∠ABC = 90o ,
BC = 2.16 , CA = 5.41
根据勾股定理得: AB =答:梯子上端A到墙的底端B的距离AB长约4.96米。(米)1、如图:一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木板,则木板的长为 ( )A.3 米 B.4 米 C.5米 D.6米C试一试:
342、隔湖有两点A、B,从与BA方向成直角 的BC方向上的点C测得CA=13米,CB=12米,则AB为 ( )A.5米 B.12米 C.10米 D.13米1312?A试一试:
3、一个直角三角形的三边长为三个连续偶数,则它的三边长分别为 ( )A 2、4、6C 4、6、8B试一试:B 6、8、10D 8、10、124、求下列2个三角形中的第三条边的长。试一试:比一比,看谁做的快 32511464如图,在Rt△ABC中,
∠c = 90°练习1.在△ABC中,∠C=90°.(1)若a=6,c=10,则b= ;(2)若a=12,b=9,则c=—— (3)若c=25,b=15,则 a = ;20练一练4. 已知△ABC中,∠C=Rt ∠,AB=c, BC=a,AC=b.
⑴如果a=12,c=13,求b;
⑵如果c=34, a∶b=8∶15,
求a,b.小结1、利用数格子的方法,探索了以直角三角形三边为边长的正方形面积的关系(即两个小正方形的面积之和等于大正方形的面积)2、探索了直角三角形的三边关系, 得到勾股定理:即直角三角形两直角边的平方和等于斜边的平方平A的面积+B的面积=C的面积a2+b2=c2
正方形A中含有 ___个小方格即A的面积是位面积------
正方形B中含有 个小方格,即B的面积是__ 个单位面积------
正方形C中含有 个小方格,即C的面积是____个单位面积。 99181899CAB(1)你能用三角形的边长表示正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?baca2+b2=c2c2a2b2在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”. 如果直角三角形两直角边分别为a,b,斜边为c,那么a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方.勾股定理在西方又称毕达哥拉斯定理!a2 + b2c2 - b2c2 - a2=c2 =a2=b2 证法(一) 有人利用这4个直角三角形拼出了右图,你能用两种方法表示大正方形的面积吗?大正方形的面积可以表示为 —————————— 又可以表示为:———————对比两种表示方法,你得到勾股定理了吗?(a+b)2验证勾股定理:证法(二) 弦图赵爽
东汉末至三国时代吴国人
为《周髀算经》作注,并著有《勾股圆方图说》。cb ? a c2 = (b ?a)2 +
= a2 ? 2ab + b2 + 2abab? c2= a2 + b2 ?(a + b)(b + a) = ?c2 + 2(?ab)
?a2 + ab + ?b2 = ?c2 + ab
? a2 + b2 = c2aabbcc伽菲尔德的证明方法.1881年,伽菲尔德就任美国第二十任总统后,人们为了纪念他对勾股定理的证明,就称这一证法称为“总统”证法。
∟∟∟证法(三)
总统证法 你还有其他证明方法吗? 例 1.在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.例题分析(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.方法小结例2:如图将长为5.41米的梯子AC斜靠在墙上,BC长
为2.16米,求梯子上端A到墙的底端B的距离AB(精确
到0.01米)分析:先把实际问题转化成数学问题。求:AB的长。解:在Rt⊿ABC中,∠ABC = 90o ,
BC = 2.16 , CA = 5.41
根据勾股定理得: AB =答:梯子上端A到墙的底端B的距离AB长约4.96米。(米)1、如图:一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木板,则木板的长为 ( )A.3 米 B.4 米 C.5米 D.6米C试一试:
342、隔湖有两点A、B,从与BA方向成直角 的BC方向上的点C测得CA=13米,CB=12米,则AB为 ( )A.5米 B.12米 C.10米 D.13米1312?A试一试:
3、一个直角三角形的三边长为三个连续偶数,则它的三边长分别为 ( )A 2、4、6C 4、6、8B试一试:B 6、8、10D 8、10、124、求下列2个三角形中的第三条边的长。试一试:比一比,看谁做的快 32511464如图,在Rt△ABC中,
∠c = 90°练习1.在△ABC中,∠C=90°.(1)若a=6,c=10,则b= ;(2)若a=12,b=9,则c=—— (3)若c=25,b=15,则 a = ;20练一练4. 已知△ABC中,∠C=Rt ∠,AB=c, BC=a,AC=b.
⑴如果a=12,c=13,求b;
⑵如果c=34, a∶b=8∶15,
求a,b.小结1、利用数格子的方法,探索了以直角三角形三边为边长的正方形面积的关系(即两个小正方形的面积之和等于大正方形的面积)2、探索了直角三角形的三边关系, 得到勾股定理:即直角三角形两直角边的平方和等于斜边的平方平A的面积+B的面积=C的面积a2+b2=c2
