勾股定理[下学期]
图片预览




文档简介
课件16张PPT。勾股定理李红娟毕达哥拉斯(公元前572-前
492年),古希腊著名的哲学家
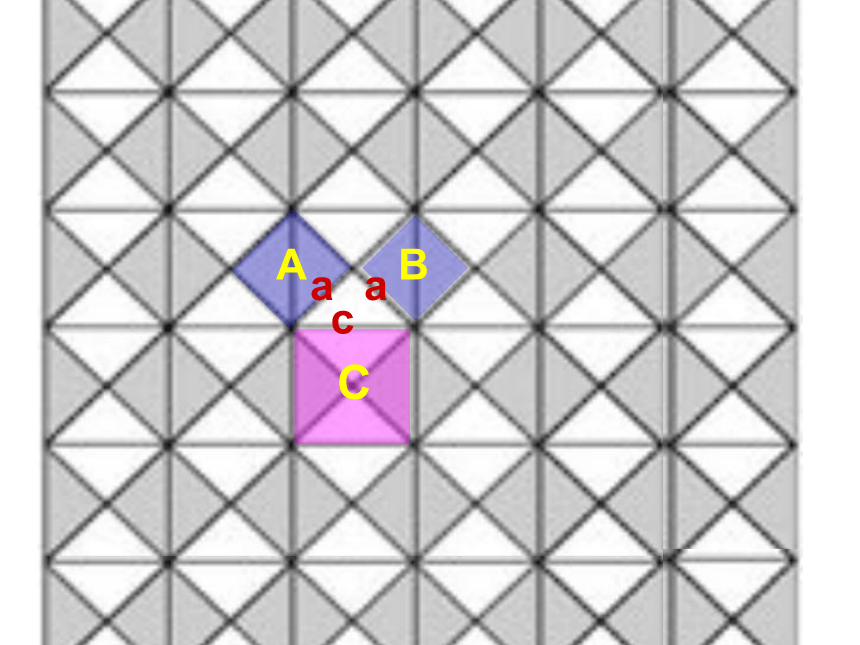
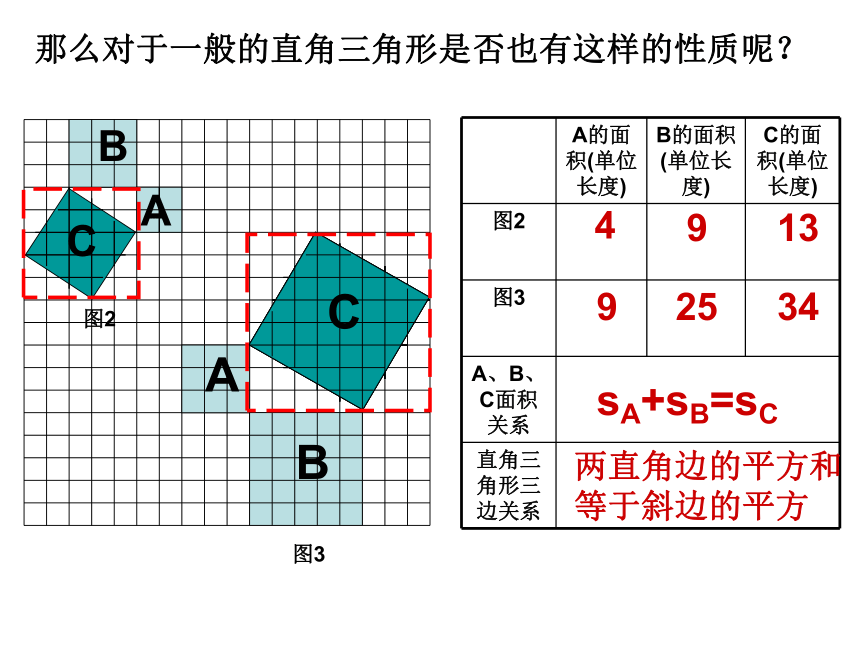
数学家,天文学家. ABCaac那么对于一般的直角三角形是否也有这样的性质呢?ABC图2图3491392534sA+sB=sC两直角边的平方和
等于斜边的平方小组活动:(1)先用你们手中的图形拼
成一大一小两个正方形。
(2)然后把两个正方形拼成
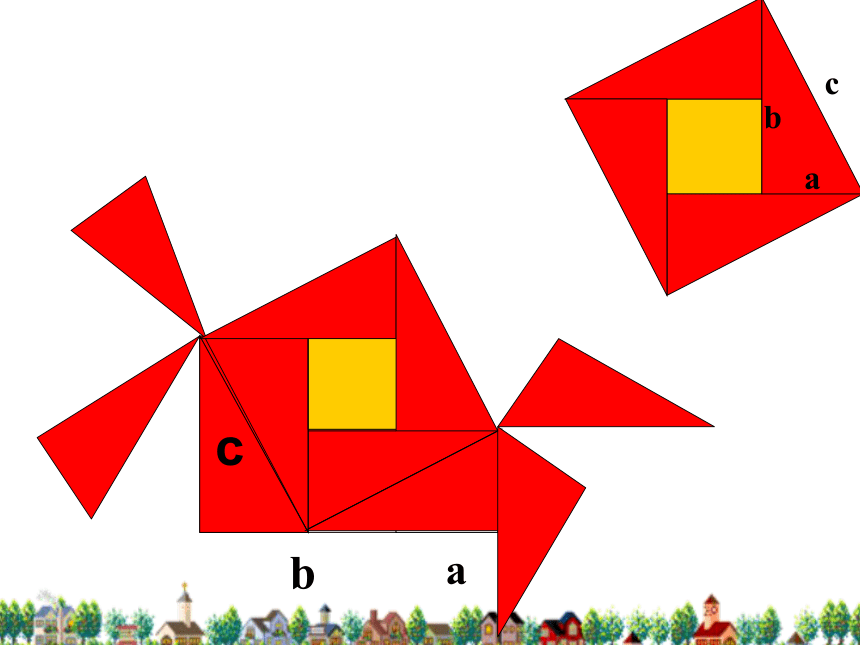
一个大正方形c 如果直角三角形两直角边分别为a,b,斜边为c,那么a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方.勾股定理毕达哥拉斯定理 驴桥定理(百牛定理)埃及三角形abc 结论变形 106ACBABC815求出下列直角三角形中未知边的边长817ABC6810今天你有什么收获?(1)通过探索发现勾股定理。(2) 会用勾股定理进行简单的计算。1、如图已知:a=3,
b=4,求c2、如图已知: c =10,a=6,求b3、如图已知: c =13,a=5,求阴影 部分的面积b笨人执竿要进屋,无奈门框拦住竿,
横多四尺竖多二,没法急得放声哭.
有个邻居聪明者,教他斜竿对两角,
笨伯依言试一试,不多不少刚抵足.
借问竿长多少数,谁人算出我佩服.执竿进屋(4) 读这首诗,并回答其中的问题。作业:收集有关勾股定理的证明方法。
492年),古希腊著名的哲学家
数学家,天文学家. ABCaac那么对于一般的直角三角形是否也有这样的性质呢?ABC图2图3491392534sA+sB=sC两直角边的平方和
等于斜边的平方小组活动:(1)先用你们手中的图形拼
成一大一小两个正方形。
(2)然后把两个正方形拼成
一个大正方形c 如果直角三角形两直角边分别为a,b,斜边为c,那么a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方.勾股定理毕达哥拉斯定理 驴桥定理(百牛定理)埃及三角形abc 结论变形 106ACBABC815求出下列直角三角形中未知边的边长817ABC6810今天你有什么收获?(1)通过探索发现勾股定理。(2) 会用勾股定理进行简单的计算。1、如图已知:a=3,
b=4,求c2、如图已知: c =10,a=6,求b3、如图已知: c =13,a=5,求阴影 部分的面积b笨人执竿要进屋,无奈门框拦住竿,
横多四尺竖多二,没法急得放声哭.
有个邻居聪明者,教他斜竿对两角,
笨伯依言试一试,不多不少刚抵足.
借问竿长多少数,谁人算出我佩服.执竿进屋(4) 读这首诗,并回答其中的问题。作业:收集有关勾股定理的证明方法。
