浙江温岭 勾股定理(2)[下学期]
文档属性
| 名称 | 浙江温岭 勾股定理(2)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-09 00:00:00 | ||
图片预览



文档简介
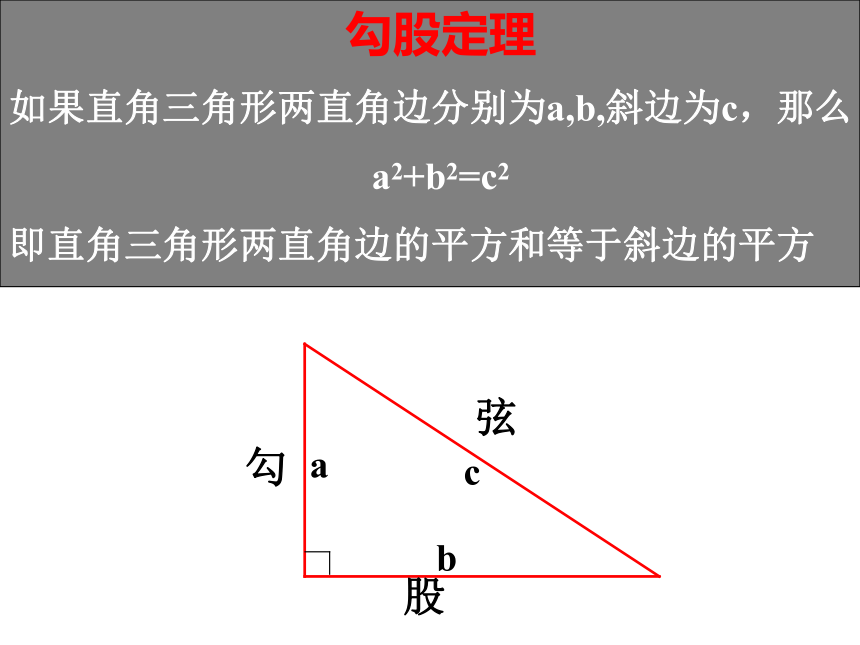
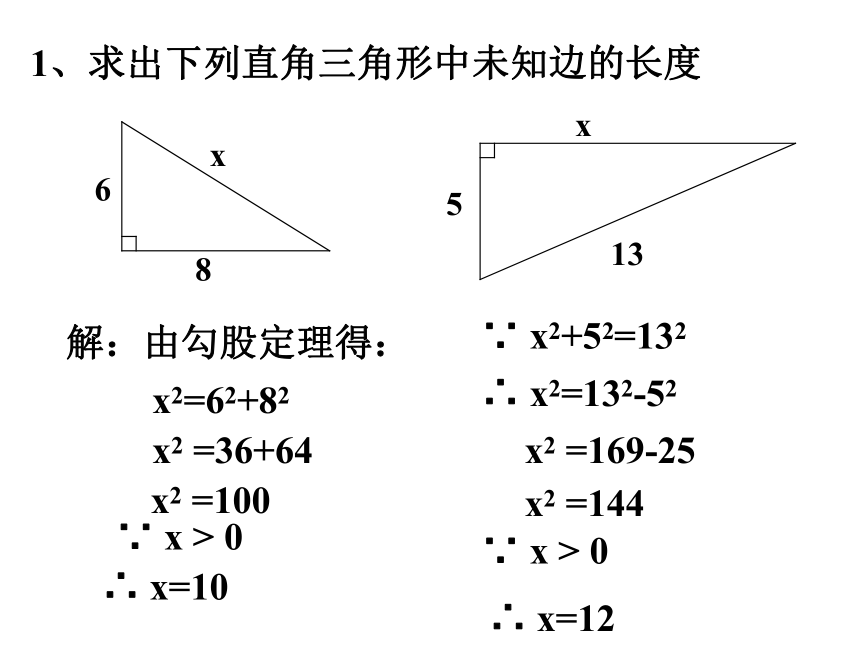
课件18张PPT。勾股定理(2)勾股弦1、求出下列直角三角形中未知边的长度解:由勾股定理得:x2 =36+64x2 =100x2=62+82∴ x=10∵ x2+52=132∴ x2=132-52x2 =169-25x2 =144∴ x=12∵ x > 0∵ x > 02、在直角三角形ABC中, ∠C=900,
已知: a=5, b=12, 求c;
已知: b=6,c=10 , 求a;
已知: a=7, c=25, 求b ;
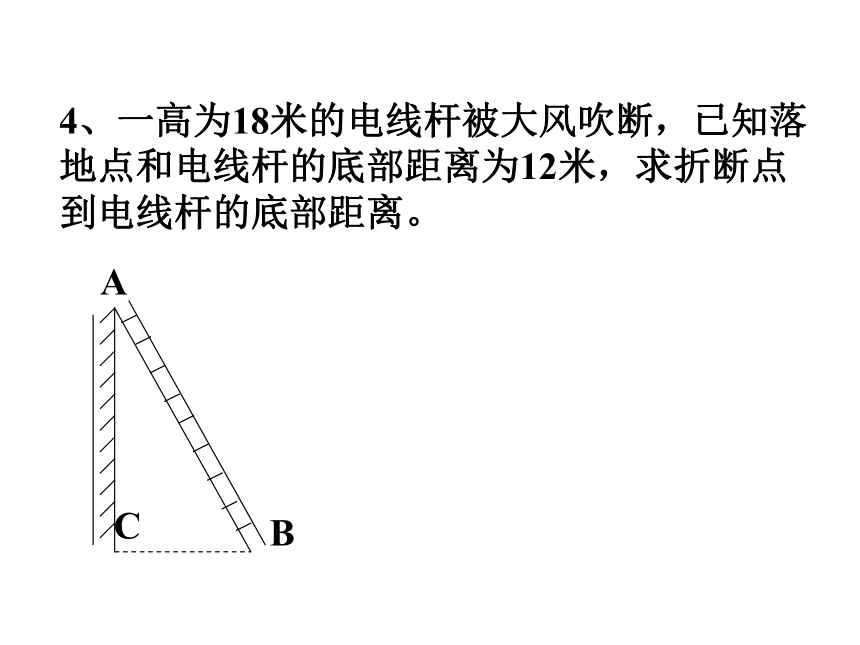
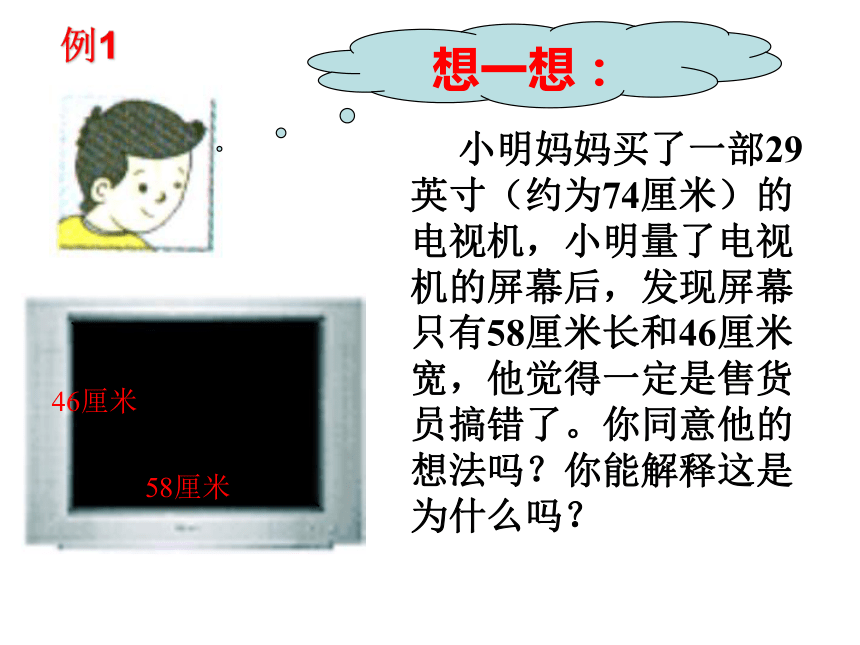
已知: a=7, c=8, 求b .3、一直角三角形的一直角边长为7, 另两条边长为两个连续整数,求这个直角三角形的周长.4、一高为18米的电线杆被大风吹断,已知落地点和电线杆的底部距离为12米,求折断点到电线杆的底部距离。 小明妈妈买了一部29英寸(约为74厘米)的电视机,小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?想一想:58厘米46厘米74厘米例1 “引葭赴岸”是《九章算术》中的一道题:
“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,
适与岸齐。问水深、葭长各几何?”例2(古题鉴赏)有一个边长为10尺的正方形池塘,
在水池正中央有一根新生的芦苇,
它高出水面1尺,如果把这根芦苇
沿与水池边垂直的方向拉向岸边,
它的顶端恰好到达岸边。请问这个
水池的深度和这根芦苇的长度各是
多少?题意是: BC为芦苇长, AB为水深, AC为池中心点距岸边的距离。 解:如图5xX+1设AB =x尺,则BC =(X+1)
尺,根据勾股定理得:
x2+52=(x+1)2即:(x+1)2- x2 =52解得:x=12
所以芦苇长为12+1=13(尺)答:水深为12尺,芦苇长为13尺。?反思:(在直角三角形中,已知一边及另两边的大小关系,也可以求出未知的边.)1、一个门框的尺寸如图所示,一块长3m、宽2.2m的薄木板能否从门框内通过?为什么?ABCD1m2m试一试,你掌握了吗?
薄 木 板
2.2m3m2.一种盛饮料的圆柱形杯(如图),测得内部底面直径为5㎝,高为12㎝,吸管放进杯里,杯口外面露出5㎝,问吸管要做多长? 5㎝12㎝5㎝?13㎝吸管长
18cm3.小明想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,求旗杆的高度1mXX+1X+1这是测量旗杆高的一种好方法哦(05年宿迁市)如图,将一根25㎝长的细木棒放入长、宽、高分别为8㎝、6㎝和10㎝的长方体无盖盒子中,则细木棒露在盒外面的最短长度是 ㎝.
思考题:8㎝6㎝10㎝?10㎝?如图,是一个三级台阶,它的每一级的长、宽
和高分别等于5cm,3cm和1cm,A和B是这个台
阶的两个相对的端点,A点上有一只蚂蚁,想
到B点去吃可口的食物.请你想一想,这只蚂蚁
从A点出发,沿着台阶面爬到B点,最短线路是
多少?思考题:古算趣题:“执竿进屋”
笨人执竿要进屋,无奈门框拦住竹,
横多四尺竖多二,没法急得放声哭。
有个邻居聪明者,教他斜竿对两角,
笨伯依言试一试,不多不少刚抵足。
借问竿长多少数,谁人算出我佩服。思考题:? 印度数学家什迦逻(1141年-1225年)曾提出过“荷花问题”:
“平平湖水清可鉴,面上半尺生红莲;
出泥不染亭亭立,忽被强风吹一边,
渔人观看忙向前,花离原位二尺远;
能算诸君请解题,湖水如何知深浅?”
请用学过的数学知识回答这个问题。你能解决?一架云梯长25米,如图斜靠在一面墙上,梯子底端离墙7米。
(1)、梯子的顶端距地面有多高?
(2)、如果 梯子的顶端下滑了4米,那么梯子的底部在水平方向滑动了4米吗?练一练?
谈一谈你的收获是。。。?你的困惑是。。。?
已知: a=5, b=12, 求c;
已知: b=6,c=10 , 求a;
已知: a=7, c=25, 求b ;
已知: a=7, c=8, 求b .3、一直角三角形的一直角边长为7, 另两条边长为两个连续整数,求这个直角三角形的周长.4、一高为18米的电线杆被大风吹断,已知落地点和电线杆的底部距离为12米,求折断点到电线杆的底部距离。 小明妈妈买了一部29英寸(约为74厘米)的电视机,小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?想一想:58厘米46厘米74厘米例1 “引葭赴岸”是《九章算术》中的一道题:
“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,
适与岸齐。问水深、葭长各几何?”例2(古题鉴赏)有一个边长为10尺的正方形池塘,
在水池正中央有一根新生的芦苇,
它高出水面1尺,如果把这根芦苇
沿与水池边垂直的方向拉向岸边,
它的顶端恰好到达岸边。请问这个
水池的深度和这根芦苇的长度各是
多少?题意是: BC为芦苇长, AB为水深, AC为池中心点距岸边的距离。 解:如图5xX+1设AB =x尺,则BC =(X+1)
尺,根据勾股定理得:
x2+52=(x+1)2即:(x+1)2- x2 =52解得:x=12
所以芦苇长为12+1=13(尺)答:水深为12尺,芦苇长为13尺。?反思:(在直角三角形中,已知一边及另两边的大小关系,也可以求出未知的边.)1、一个门框的尺寸如图所示,一块长3m、宽2.2m的薄木板能否从门框内通过?为什么?ABCD1m2m试一试,你掌握了吗?
薄 木 板
2.2m3m2.一种盛饮料的圆柱形杯(如图),测得内部底面直径为5㎝,高为12㎝,吸管放进杯里,杯口外面露出5㎝,问吸管要做多长? 5㎝12㎝5㎝?13㎝吸管长
18cm3.小明想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,求旗杆的高度1mXX+1X+1这是测量旗杆高的一种好方法哦(05年宿迁市)如图,将一根25㎝长的细木棒放入长、宽、高分别为8㎝、6㎝和10㎝的长方体无盖盒子中,则细木棒露在盒外面的最短长度是 ㎝.
思考题:8㎝6㎝10㎝?10㎝?如图,是一个三级台阶,它的每一级的长、宽
和高分别等于5cm,3cm和1cm,A和B是这个台
阶的两个相对的端点,A点上有一只蚂蚁,想
到B点去吃可口的食物.请你想一想,这只蚂蚁
从A点出发,沿着台阶面爬到B点,最短线路是
多少?思考题:古算趣题:“执竿进屋”
笨人执竿要进屋,无奈门框拦住竹,
横多四尺竖多二,没法急得放声哭。
有个邻居聪明者,教他斜竿对两角,
笨伯依言试一试,不多不少刚抵足。
借问竿长多少数,谁人算出我佩服。思考题:? 印度数学家什迦逻(1141年-1225年)曾提出过“荷花问题”:
“平平湖水清可鉴,面上半尺生红莲;
出泥不染亭亭立,忽被强风吹一边,
渔人观看忙向前,花离原位二尺远;
能算诸君请解题,湖水如何知深浅?”
请用学过的数学知识回答这个问题。你能解决?一架云梯长25米,如图斜靠在一面墙上,梯子底端离墙7米。
(1)、梯子的顶端距地面有多高?
(2)、如果 梯子的顶端下滑了4米,那么梯子的底部在水平方向滑动了4米吗?练一练?
谈一谈你的收获是。。。?你的困惑是。。。?
