鲁教版(五四学制)九年级上册1.1反比例函数课件 (共20张PPT)
文档属性
| 名称 | 鲁教版(五四学制)九年级上册1.1反比例函数课件 (共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-20 08:46:05 | ||
图片预览







文档简介
(共20张PPT)
引入新课
老师从家开车到东营区第一中学,路程大约20千米,在老师行驶的过程中想到了一些问题,想和同学们一起交流一下:
东营区第一中学
引入新课
路程(20)
速度(v)、时间(t)
1、找出变量与常量
变量:_______________
常量:______________
2、表示上述过程中几个量之间的关系_____________
vt=20
3、利用所列关系式,填写下列表格
4、观察表格,你能得出什么结论?
引入新课
vt=20
①时间t随着速度v的变化而变化
②速度×时间是一个定值
1.1 反比例函数
数学鲁教版 九上
1.理解反比例函数的概念.
2.能判断一个给定的函数是否为反比例函数.
3.会用待定系数法求反比例函数的解析式.
学习目标
1、学校要建一个面积为100m2的矩形花坛,花坛的长y(m)随宽x(m)的变化而变化.
2、已知两个实数的乘积为-8,如果其中一个因数为p,另一个因数为q,则q与p的函数关系是什么?
探究一
用函数关系式表示下列问题中两个量之间的关系
探究一
观察三个表达式,它们在形式上有什么共同特点?
1、都有2个变量
2、等号右边是分式的形式且分子是一个常数
t
概念形成
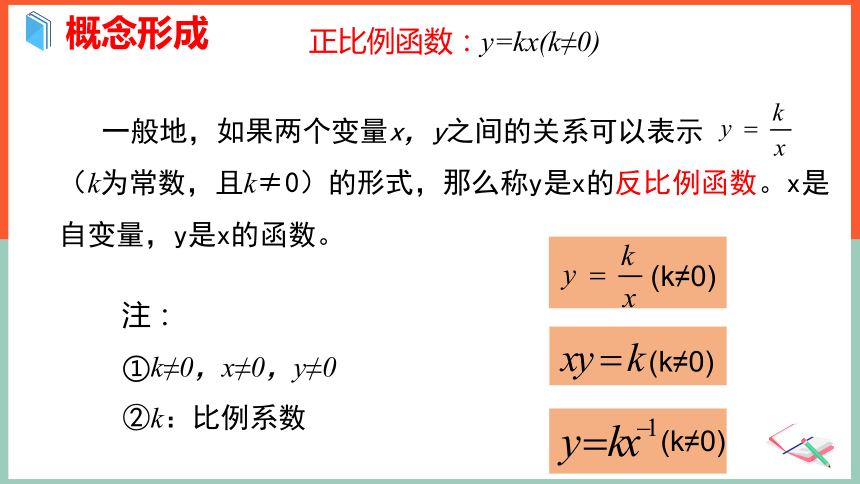
注:
①k≠0,x≠0,y≠0
②k:比例系数
一般地,如果两个变量x,y之间的关系可以表示 (k为常数,且k≠0)的形式,那么称y是x的反比例函数。x是自变量,y是x的函数。
(k≠0)
(k≠0)
(k≠0)
正比例函数:y=kx(k≠0)
下列式子是不是反比例函数,若是,指出k的值?
跟踪练习
y=x-2
xy=2
√ k=5
√ k=2
×
×
×
√ k=-2
×
√
×
观察发现
xy=2
(k≠0)
(k≠0)
(k≠0)
(1)已知函数 是反比例函数,则m______
(2)已知函数y=3xm-7是反比例函数,则m=______
(3)已知函数 是反比例函数,则m=______
6
≠3
1
小结:判断判断字母的取值应注意的条件
(1)自变量的指数为-1
(2)k≠0
同桌合作,1人写反比例函数的例子,另1人说出k的值
showtime
例:已知y是x的反比例函数,当x=-3时,y=4
(1)写出y与x之间的函数关系式;
(2)当x=6时,求y的值
待定系数法
探究二
解:
求
写
设
代
(2)把x=6代入
(1)设 (k≠0)
当x=-3时,y=4,
有
所以k=-12
所以
(1)写出这个反比例函数的表达式;
(2)根据函数表达式完成表格.
变式:y是x的反比例函数,下表给出了x与y的一些值:
x -2 -1 1 3
y 2 -1
-3
1
4
-4
-2
2
小组讨论:列举实际生活学习中具有反比例函数的例子(自己给出常数k的值),并列出函数表达式
showtime
谈收获
这节课你学会了什么?
你有哪些收获?
还有哪些疑问?
定义
待定系数法
反比例函数
1、设
2、代
3、求
4、写
建模、类比思想
1、定义
2、3种形式
课堂检测
1、当m=_______时,函数 是x的反比例函数?
2、一定体积的面团做成拉面,拉面的总长度y(m)是拉面的横截面面积
S(mm2)的反比例函数,已知当S=4mm2时,y=32m,
(1)求y与S的表达式。
(2)若工人师傅将面团拉成160根拉面,每根长0.5m时为成品,求此时的
横截面面积.
-2
1.6mm2
布置作业
必做题: 习题1.1 T1-5
选做题:
列举实际生活中具有反比例函数的例子
谢谢大家
引入新课
老师从家开车到东营区第一中学,路程大约20千米,在老师行驶的过程中想到了一些问题,想和同学们一起交流一下:
东营区第一中学
引入新课
路程(20)
速度(v)、时间(t)
1、找出变量与常量
变量:_______________
常量:______________
2、表示上述过程中几个量之间的关系_____________
vt=20
3、利用所列关系式,填写下列表格
4、观察表格,你能得出什么结论?
引入新课
vt=20
①时间t随着速度v的变化而变化
②速度×时间是一个定值
1.1 反比例函数
数学鲁教版 九上
1.理解反比例函数的概念.
2.能判断一个给定的函数是否为反比例函数.
3.会用待定系数法求反比例函数的解析式.
学习目标
1、学校要建一个面积为100m2的矩形花坛,花坛的长y(m)随宽x(m)的变化而变化.
2、已知两个实数的乘积为-8,如果其中一个因数为p,另一个因数为q,则q与p的函数关系是什么?
探究一
用函数关系式表示下列问题中两个量之间的关系
探究一
观察三个表达式,它们在形式上有什么共同特点?
1、都有2个变量
2、等号右边是分式的形式且分子是一个常数
t
概念形成
注:
①k≠0,x≠0,y≠0
②k:比例系数
一般地,如果两个变量x,y之间的关系可以表示 (k为常数,且k≠0)的形式,那么称y是x的反比例函数。x是自变量,y是x的函数。
(k≠0)
(k≠0)
(k≠0)
正比例函数:y=kx(k≠0)
下列式子是不是反比例函数,若是,指出k的值?
跟踪练习
y=x-2
xy=2
√ k=5
√ k=2
×
×
×
√ k=-2
×
√
×
观察发现
xy=2
(k≠0)
(k≠0)
(k≠0)
(1)已知函数 是反比例函数,则m______
(2)已知函数y=3xm-7是反比例函数,则m=______
(3)已知函数 是反比例函数,则m=______
6
≠3
1
小结:判断判断字母的取值应注意的条件
(1)自变量的指数为-1
(2)k≠0
同桌合作,1人写反比例函数的例子,另1人说出k的值
showtime
例:已知y是x的反比例函数,当x=-3时,y=4
(1)写出y与x之间的函数关系式;
(2)当x=6时,求y的值
待定系数法
探究二
解:
求
写
设
代
(2)把x=6代入
(1)设 (k≠0)
当x=-3时,y=4,
有
所以k=-12
所以
(1)写出这个反比例函数的表达式;
(2)根据函数表达式完成表格.
变式:y是x的反比例函数,下表给出了x与y的一些值:
x -2 -1 1 3
y 2 -1
-3
1
4
-4
-2
2
小组讨论:列举实际生活学习中具有反比例函数的例子(自己给出常数k的值),并列出函数表达式
showtime
谈收获
这节课你学会了什么?
你有哪些收获?
还有哪些疑问?
定义
待定系数法
反比例函数
1、设
2、代
3、求
4、写
建模、类比思想
1、定义
2、3种形式
课堂检测
1、当m=_______时,函数 是x的反比例函数?
2、一定体积的面团做成拉面,拉面的总长度y(m)是拉面的横截面面积
S(mm2)的反比例函数,已知当S=4mm2时,y=32m,
(1)求y与S的表达式。
(2)若工人师傅将面团拉成160根拉面,每根长0.5m时为成品,求此时的
横截面面积.
-2
1.6mm2
布置作业
必做题: 习题1.1 T1-5
选做题:
列举实际生活中具有反比例函数的例子
谢谢大家
