勾股定理[下学期]
图片预览




文档简介
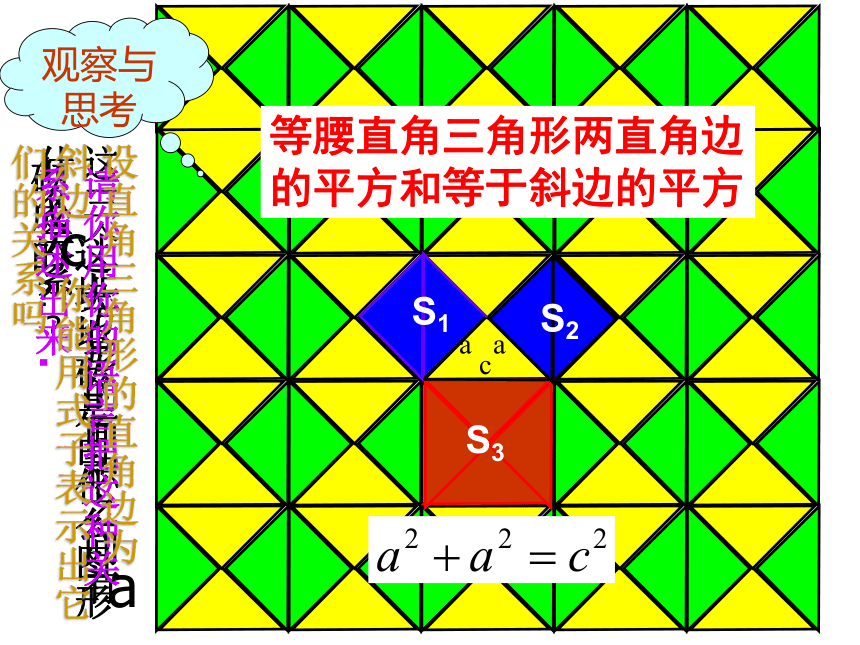
课件21张PPT。探索勾股定理 相传2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家的用砖铺成的地面中反映了直角三角形三边的某种数量关系。同学们我们也来观察下图中的地面,试试看你能发现这个规律吗?观察与思考请你用你的语言把这种关系描述出来.等腰直角三角形两直角边的平方和等于斜边的平方aacS1S2S3aac探究:
等腰三角形有上述性质,其它
的直角三角形也有这个性质吗?
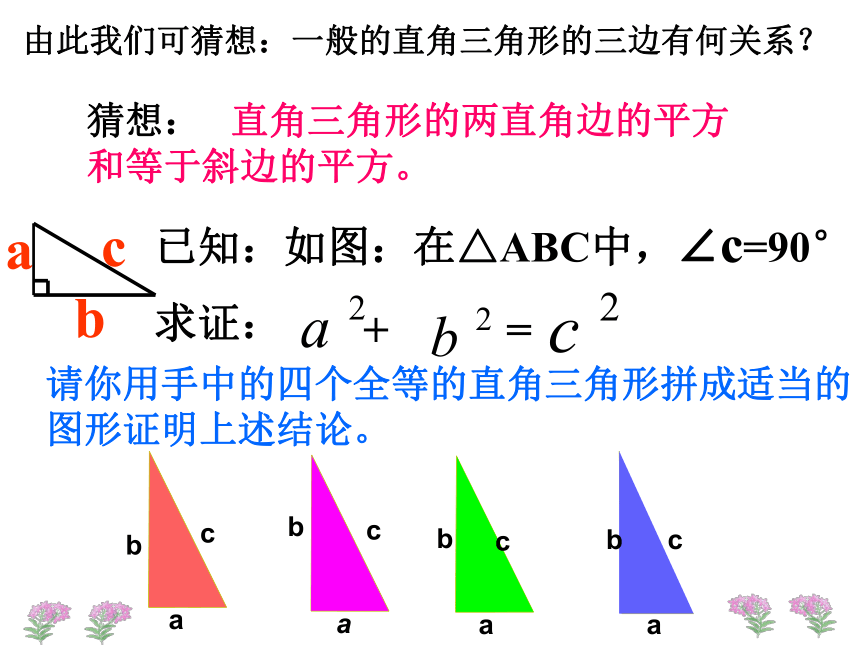
等腰直角三角形两直角边的平方和等于斜边的平方S1S2S3abc由此我们可猜想:一般的直角三角形的三边有何关系?猜想: 直角三角形的两直角边的平方和等于斜边的平方。已知:如图:在△ABC中,∠c=90°
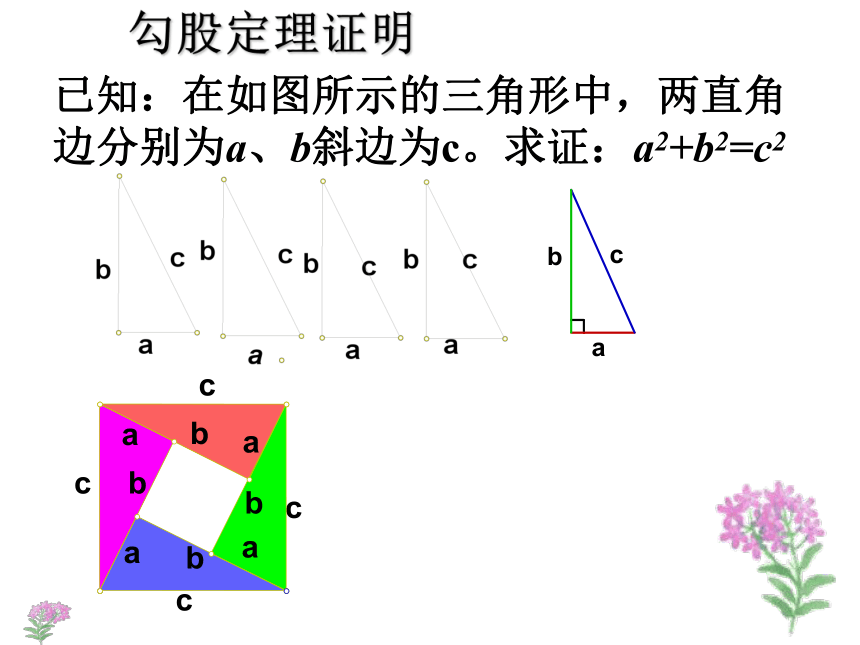
求证:请你用手中的四个全等的直角三角形拼成适当的
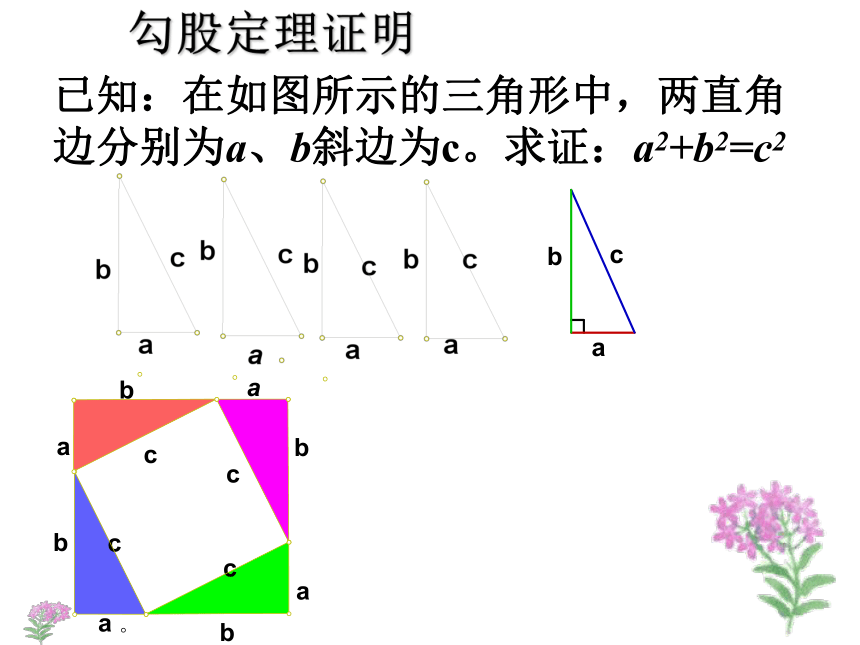
图形证明上述结论。勾股定理证明已知:在如图所示的三角形中,两直角边分别为a、b斜边为c。求证:a2+b2=c2勾股定理证明已知:在如图所示的三角形中,两直角边分别为a、b斜边为c。求证:a2+b2=c2有趣的总统证法aabbcc∴ a2 + b2 = c2用赵爽弦图证明勾股定理=毕达哥拉斯证法c2a2b2? a2 + b2 = c2 如图,将梯子AC斜靠在墙上,梯子的下端到墙角的距离BC长为5米, 梯子上端A到墙的底边的垂直距离AB为12,求梯子AC的长.ABCC1A1 现有一个同学不小心碰到梯子,使其下端C向左滑动1米到了C1点,问梯子的上端A下滑了多少?学以致用1、本节课我们经历了怎样的过程? 经历了从实际问题引入数学问题然后发现定理,再到探索定理,最后学会验证定理及应用定理解决实际问题的过程。 2、本节课我们学到了什么? 通过本节课的学习我们不但知道了著名的勾股定理,还知道从特殊到一般的探索方法及借助于图形的面积来探索、验证数学结论的数形结合思想。3、学了本节课后你有什么感想? 很多的数学结论存在于平常的生活中,需要我们用数学的眼光去观察、思考、发现,这节课我们还受到了数学文化辉煌历史的教育。1、作业本(1) 第19 页
2 、利用方格纸探索锐角三角形
或钝角三角形的三边关系。作 业无字证明青出 ab无字证明c青出华罗庚青朱出入图无字证明a2b2证明三证明三证明4c2? a2 + b2 = c2c著名画家达芬奇
等腰三角形有上述性质,其它
的直角三角形也有这个性质吗?
等腰直角三角形两直角边的平方和等于斜边的平方S1S2S3abc由此我们可猜想:一般的直角三角形的三边有何关系?猜想: 直角三角形的两直角边的平方和等于斜边的平方。已知:如图:在△ABC中,∠c=90°
求证:请你用手中的四个全等的直角三角形拼成适当的
图形证明上述结论。勾股定理证明已知:在如图所示的三角形中,两直角边分别为a、b斜边为c。求证:a2+b2=c2勾股定理证明已知:在如图所示的三角形中,两直角边分别为a、b斜边为c。求证:a2+b2=c2有趣的总统证法aabbcc∴ a2 + b2 = c2用赵爽弦图证明勾股定理=毕达哥拉斯证法c2a2b2? a2 + b2 = c2 如图,将梯子AC斜靠在墙上,梯子的下端到墙角的距离BC长为5米, 梯子上端A到墙的底边的垂直距离AB为12,求梯子AC的长.ABCC1A1 现有一个同学不小心碰到梯子,使其下端C向左滑动1米到了C1点,问梯子的上端A下滑了多少?学以致用1、本节课我们经历了怎样的过程? 经历了从实际问题引入数学问题然后发现定理,再到探索定理,最后学会验证定理及应用定理解决实际问题的过程。 2、本节课我们学到了什么? 通过本节课的学习我们不但知道了著名的勾股定理,还知道从特殊到一般的探索方法及借助于图形的面积来探索、验证数学结论的数形结合思想。3、学了本节课后你有什么感想? 很多的数学结论存在于平常的生活中,需要我们用数学的眼光去观察、思考、发现,这节课我们还受到了数学文化辉煌历史的教育。1、作业本(1) 第19 页
2 、利用方格纸探索锐角三角形
或钝角三角形的三边关系。作 业无字证明青出 ab无字证明c青出华罗庚青朱出入图无字证明a2b2证明三证明三证明4c2? a2 + b2 = c2c著名画家达芬奇
