2021-2022学年河北省沧州市孟村县九年级(上)期末数学试卷 (word解析版)
文档属性
| 名称 | 2021-2022学年河北省沧州市孟村县九年级(上)期末数学试卷 (word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 770.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-20 08:41:11 | ||
图片预览




文档简介
2021-2022学年河北省沧州市孟村县九年级(上)期末数学试卷
一、选择题.(本大题有16个小题,共42分.1~10小题各3分;11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(3分)抛物线y=x2+2x﹣3与y轴的交点坐标是( )
A.(0,﹣3) B.(﹣3,0) C.(0,2) D.(2,0)
2.(3分)已知在 Rt△ABC中,∠C=90°,cosA=,则∠B的度数为( )
A.30° B.45° C.60° D.无法确定
3.(3分)已知△ABC∽△DEF,相似比为,若△ABC的周长为3,则△DEF的周长为( )
A.1 B.3 C.9 D.27
4.(3分)如图,AB是⊙O的直径,CO⊥AB,点D在直径AB上方的⊙O上,连接BD,CD,则∠CDB的度数是( )
A.30° B.45° C.60° D.75°
5.(3分)三张质地、大小、背面完全相同的卡片上,正面分别画有圆、平行四边形和等边三角形三个图案.现把它们的正面向下随机摆放在桌面上,从中任意抽出一张,则抽出的卡片正面图案是中心对称图形的概率为( )
A. B. C. D.
6.(3分)如图是东西流向且河岸平行的一段河道,点A,B分别为两岸上一点,且点B在点A正南方向,由点B向正西方向走a米到达点C,此时测得点C在点A的南偏西50°方向上,则河宽AB的长为( )
A.atan50°米 B.米 C.米 D.米
7.(3分)关于抛物线y=﹣3(x﹣1)2+5,下列说法正确的是( )
A.开口向上
B.对称轴为直线x=﹣1
C.当x≥1时,y随x的增大而减小
D.该抛物线向上平移2个单位长度后可经过原点
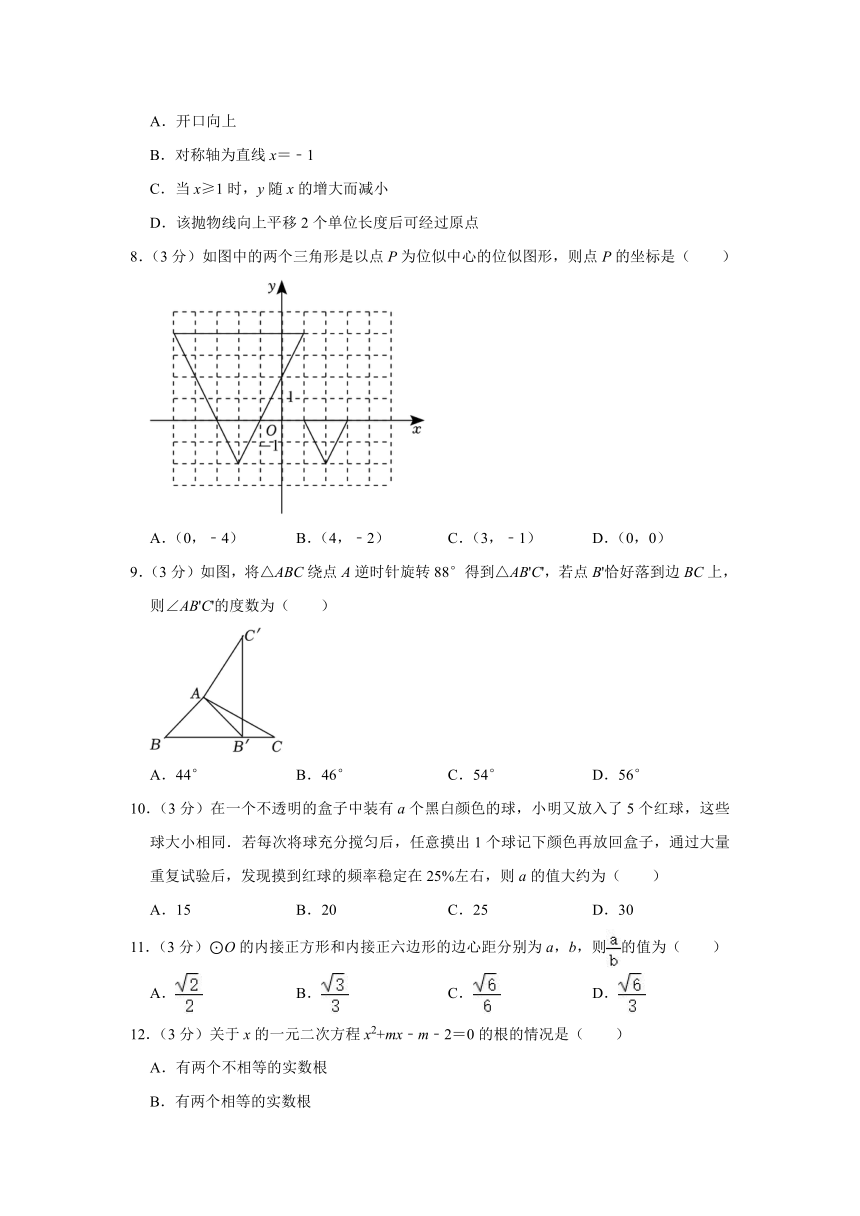
8.(3分)如图中的两个三角形是以点P为位似中心的位似图形,则点P的坐标是( )
A.(0,﹣4) B.(4,﹣2) C.(3,﹣1) D.(0,0)
9.(3分)如图,将△ABC绕点A逆时针旋转88°得到△AB'C',若点B'恰好落到边BC上,则∠AB'C'的度数为( )
A.44° B.46° C.54° D.56°
10.(3分)在一个不透明的盒子中装有a个黑白颜色的球,小明又放入了5个红球,这些球大小相同.若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子,通过大量重复试验后,发现摸到红球的频率稳定在25%左右,则a的值大约为( )
A.15 B.20 C.25 D.30
11.(3分)⊙O的内接正方形和内接正六边形的边心距分别为a,b,则的值为( )
A. B. C. D.
12.(3分)关于x的一元二次方程x2+mx﹣m﹣2=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.实数根的个数由m的值确定
13.(3分)如图,矩形ABCD在平面直角坐标系中,点A,D分别在反比例函数和的图象上,点B,C在x轴上,若S矩形ABCD=4,则k的值为( )
A.12 B.7 C.﹣12 D.﹣7
14.(3分)如图,⊙O是Rt△ABC的内切圆,点D,E是切点,则下列说法不正确的是( )
A.CD=CE
B.∠ABO=45°
C.△BCO的外心在△BCO的外面
D.四边形ODCE没有外接圆
15.(3分)如图,在△ABC中,∠B=90°,AB=6cm,BC=7cm.点P从点B开始沿边BA向点A以2cm/s的速度移动,同时点Q从点C开始沿边CB向点B以1cm/s的速度移动,当其中一点到达终点时,另一点随即停止.当四边形APQC的面积为11cm2时,点P的运动时间为( )
A.1s B.1s或2.5s C.2s D.2s或5s
16.(3分)若直线y=m(m为常数)与函数的图象恒有三个不同的交点,则m的取值范围是( )
A.0<m<2 B.0<m≤2 C.0<m<4 D.0<m≤4
二、填空题.(本大题有3个小题,每小题有2个空,每空2分,共12分.把答案写在题中横线上)
17.(4分)若点A(a﹣2,b+2)与点B(4,﹣3)关于原点对称.
(1)点A在第 象限;
(2)a﹣b的值为 .
18.(4分)已知y与x成反比例,当x=﹣1时,y=﹣6.
(1)y与x的函数解析式为 ;
(2)若点A(a,﹣4),B(b,﹣8)都在该反比例函数的图象上,则a,b的大小关系是 .
19.(4分)如图,已知在△ABC中,AB=AC=5,BC=8,点P在边BC上(点P与点B,C不重合),∠APF=∠B,射线PF与边AC交于点F,过点A作BC的平行线,交射线PF于点Q.
(1)若BP=2,则CF的长为 ;
(2)当△AFQ是等腰三角形时,BP的长为 .
三、解答题.(本大题共7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
20.(8分)用适当的方法解下列方程.
(1)x2﹣2x﹣4=0;
(2)(x﹣5)(x+2)=8.
21.(9分)如图,在△ABC中,∠C=90°,AC=3,点D在边BC上,且tan∠CAD=.
(1)求cos∠CAD的值;
(2)若BD=2CD,求sinB的值.
22.(9分)某新冠疫苗接种点有4个完全相同的冷藏箱用来储存疫苗,同一冷藏箱里的疫苗都来自同一厂家,其有两箱储存A厂家的疫苗,另两箱分别储存B厂家和C厂家的疫苗.
(1)如果将4个箱子随机送往4个接种台,每个接种台接受一个箱子,那么1号台恰好收到A厂家疫苗的概率是 ;
(2)如果从中随机拿出两个箱子,送往1号和2号接种台,请用列表或画树状图的方法求拿出的两个冷藏箱里有A厂家疫苗的概率.
23.(9分)如图,已知点A(a,2),B(﹣1,b)是直线y=2x﹣6与反比例函数y=图象的交点,且该直线与y轴交于点C.
(1)求该反比例函数的解析式;
(2)连接OA,OB,求△AOB的面积;
(3)根据图象,直接写出不等式2x﹣6的解集.
24.(9分)如图,正方形ABCD的边长为4,动点P在边AB上从点B沿BA向点A运动(点P不与点A,B重合),连接PC.过点P作PE⊥PC,PE交AD于点Q.
(1)求证:△APQ∽△BCP;
(2)若S△APQ:S△BCP=1:16,求AQ的长度;
(3)连接CQ.试判断当点P运动到边AB的什么位置时,△PCQ∽△BCP?并说明理由.
25.(10分)如图1,已知∠ABC=60°,点O在射线BC上,且OB=4.以点O为圆心,r(r>0)为半径作⊙O,交直线BC于点D,E.
(1)当⊙O与∠ABC只有两个交点时,r的取值范围是 ;
(2)当时,将射线BA绕点B按顺时针方向旋转α(0°<α<180°).
①当α为多少时,射线BA与⊙O相切;
②如图2,射线BA与⊙O交于M,N两点,若MN=OB,求阴影部分的面积.
26.(12分)一小球M从斜坡OA上的点O处抛出,球的抛出路线是抛物线的一部分,建立如图所示的平面直角坐标系,斜坡可以用一次函数刻画.若小球到达最高点的坐标为(4,8).
(1)求抛物线的函数解析式(不写自变量x的取值范围);
(2)小球在斜坡上的落点A的垂直高度为 米;
(3)若要在斜坡OA上的点B处竖直立一个高4米的广告牌,点B的横坐标为2,请判断小球M能否飞过这个广告牌?通过计算说明理由;
(4)求小球M在飞行的过程中离斜坡OA的最大高度.
2021-2022学年河北省沧州市孟村县九年级(上)期末数学试卷
参考答案与试题解析
一、选择题.(本大题有16个小题,共42分.1~10小题各3分;11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(3分)抛物线y=x2+2x﹣3与y轴的交点坐标是( )
A.(0,﹣3) B.(﹣3,0) C.(0,2) D.(2,0)
【分析】令x=0,求出相应的y的值,即可得到抛物线y=x2+4x﹣1与y轴的交点坐标.
【解答】解:∵抛物线y=x2+2x﹣3,
∴当x=0时,y=﹣3,
即抛物线y=x2+2x﹣3与y轴的交点坐标是(0,﹣3),
故选:A.
2.(3分)已知在 Rt△ABC中,∠C=90°,cosA=,则∠B的度数为( )
A.30° B.45° C.60° D.无法确定
【分析】直接利用特殊角的三角函数值得出∠A的度数,进而利用直角三角形的性质得出答案.
【解答】解:在 Rt△ABC中,∠C=90°,
∵cosA=,
∴∠A=60°,
∴∠B的度数为:90°﹣60°=30°.
故选:A.
3.(3分)已知△ABC∽△DEF,相似比为,若△ABC的周长为3,则△DEF的周长为( )
A.1 B.3 C.9 D.27
【分析】根据相似三角形的性质得△ABC的周长:△DEF的周长=1:3,然后把△ABC的周长=3代入可计算出△DEF的周长.
【解答】解:∵△ABC与△DEF的相似比为1:3,
∴△ABC的周长:△DEF的周长=1:3,
∴△DEF的周长=3×3=9.
故选:C.
4.(3分)如图,AB是⊙O的直径,CO⊥AB,点D在直径AB上方的⊙O上,连接BD,CD,则∠CDB的度数是( )
A.30° B.45° C.60° D.75°
【分析】利用圆周角定理∠CDB==45°.
【解答】解:∵AB是⊙O的直径,CO⊥AB,
∴∠AOC=∠BOC=90°,
∴∠CDB===45°.
故选:B.
5.(3分)三张质地、大小、背面完全相同的卡片上,正面分别画有圆、平行四边形和等边三角形三个图案.现把它们的正面向下随机摆放在桌面上,从中任意抽出一张,则抽出的卡片正面图案是中心对称图形的概率为( )
A. B. C. D.
【分析】共有3个等可能的结果,抽出的卡片正面图案都是中心对称图形的结果有2个,再由概率公式求解即可.
【解答】解:圆、平行四边形和等边三角形三个图案是中心对称图形的是圆、平行四边形.从中任意抽出一张,抽出的卡片正面图案都是中心对称图形的结果有2个,
∴抽出的卡片正面图案都是中心对称图形的概率为,
故选:D.
6.(3分)如图是东西流向且河岸平行的一段河道,点A,B分别为两岸上一点,且点B在点A正南方向,由点B向正西方向走a米到达点C,此时测得点C在点A的南偏西50°方向上,则河宽AB的长为( )
A.atan50°米 B.米 C.米 D.米
【分析】根据正切的定义解答即可.
【解答】解:在Rt△ABC中,∠C=90°,∠BAC=50°,BC=a米,
∵tan∠BAC=,
∴AB==(米),
故选:D.
7.(3分)关于抛物线y=﹣3(x﹣1)2+5,下列说法正确的是( )
A.开口向上
B.对称轴为直线x=﹣1
C.当x≥1时,y随x的增大而减小
D.该抛物线向上平移2个单位长度后可经过原点
【分析】由二次函数顶点式解析式,根据二次函数的性质进行解答即可.
【解答】解:由抛物线解析式可得,
a<0,
∴开口向下,A错误;
对称轴x=1,B错误;
∴当x≥1时,y随x的增大而减小,C正确;
∵顶点坐标为(1,5),
∴该抛物线向上平移2个单位后顶点为(1,7),
∴平移后抛物线解析式为y=﹣3(x﹣1)2+7,
令x=0,则y=4≠0,
∴平移后抛物线不经过原点,
故D错误.
故选:C.
8.(3分)如图中的两个三角形是以点P为位似中心的位似图形,则点P的坐标是( )
A.(0,﹣4) B.(4,﹣2) C.(3,﹣1) D.(0,0)
【分析】根据位似变换的概念找出位似中心.
【解答】解:对应点所连线段所在的直线交于(4,﹣2)
∴点P的坐标为(4,﹣2),
故选:B.
9.(3分)如图,将△ABC绕点A逆时针旋转88°得到△AB'C',若点B'恰好落到边BC上,则∠AB'C'的度数为( )
A.44° B.46° C.54° D.56°
【分析】根据旋转的性质可求得AB=AB′,∠AB′C′的度数.
【解答】解:由旋转的性质可知:AB=AB′,旋转角∠BAB′=88°,
∴∠B=∠AB′C′,
∵AB=AB′,
∴∠B=∠BB′A=46°,
∴∠AB'C'=46°.
故选:B.
10.(3分)在一个不透明的盒子中装有a个黑白颜色的球,小明又放入了5个红球,这些球大小相同.若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子,通过大量重复试验后,发现摸到红球的频率稳定在25%左右,则a的值大约为( )
A.15 B.20 C.25 D.30
【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手,列出方程求解.
【解答】解:由题意可得,×100%=25%,
解得,a=15,
经检验:a=15是原分式方程的解,
所以a=15,
故选:A.
11.(3分)⊙O的内接正方形和内接正六边形的边心距分别为a,b,则的值为( )
A. B. C. D.
【分析】设⊙O的半径为R,如图,连接OB,OC,根据正六边形的性质得到∠BOC=60°,求得OB=OC=BC=R,根据勾股定理得到OM==,如图,连接OB,OC,根据正方形的性质得到∠BOC=90°,求得BC=OB=R,根据等腰直角三角形的性质得到ON=BC=R,于是得到结论.
【解答】解:设⊙O的半径为R,
如图,连接OB,OC,
∵多边形ABCDEF是正六边形,
∴∠BOC=60°,
∴OB=OC=BC=R,
∵OM⊥BC,
∴BM=BC=,
∴OM==,
如图,连接OB,OC,
∵四边形ABCD是正方形,
∴∠BOC=90°,
∴BC=OB=R,
∵ON⊥BC,
∴ON=BC=R,
∴==,
故选:D.
12.(3分)关于x的一元二次方程x2+mx﹣m﹣2=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.实数根的个数由m的值确定
【分析】先计算判别式的值,再配方得到Δ=(m+2)2+4>0,从而可判断方程根的情况.
【解答】解:∵Δ=m2﹣4(﹣m﹣2)
=m2+4m+8
=(m+2)2+4>0,
∴方程有两个不相等的实数根.
故选:A.
13.(3分)如图,矩形ABCD在平面直角坐标系中,点A,D分别在反比例函数和的图象上,点B,C在x轴上,若S矩形ABCD=4,则k的值为( )
A.12 B.7 C.﹣12 D.﹣7
【分析】延长AD,交y轴于E,如图,利用矩形的性质得AE∥x轴,AB⊥x轴,DC⊥x轴,则利用反比例函数的比例系数k的几何意义得到S矩形CDEO=|﹣3|=3,S矩形ABOE=|k|,进而得出|k|=3+4=7,即可求出k=﹣7.
【解答】解:延长AD,交y轴于E,如图,
∵四边形ABCD为矩形,
∴AE∥x轴,AB⊥x轴,DC⊥x轴,
∵点A,D分别在反比例函数和的图象上,点B,C在x轴上,
∴S矩形CDEO=|﹣3|=3,S矩形ABOE=|k|,
∵S矩形ABCD=4,
∴|k|=3+4=7,
∵k<0.
∴k=﹣7.
故选:D.
14.(3分)如图,⊙O是Rt△ABC的内切圆,点D,E是切点,则下列说法不正确的是( )
A.CD=CE
B.∠ABO=45°
C.△BCO的外心在△BCO的外面
D.四边形ODCE没有外接圆
【分析】根据三角形内切圆的性质得到OC平分∠ACB,OD⊥BC,OE⊥AC,根据角平分线的性质得到CD=CE,故A正确;根据角平分线的定义得到∠ABO=∠CBO==45°,故B正确;根据全等三角形的性质得到∠COD=∠COE,根据三角形的内角和定理得到∠BOC=90°+A>90°是钝角三角形,推出△BCO的外心在△BCO的外面,故C正确;推出点O、D、C、E四点共圆,得到四边形ODCE有外接圆,故D错误.
【解答】解:∵⊙O是Rt△ABC的内切圆,
∴OC平分∠ACB,OD⊥BC,OE⊥AC,
∴CD=CE,故A正确;
∵⊙O是Rt△ABC的内切圆,
∴OB平分∠ABC,
∵∠ABC=90°,
∴∠ABO=∠CBO==45°,故B正确;
∵OD⊥BC,
∴∠BOD=45°,
在Rt△CDO与Rt△CEO中,
,
∴Rt△CDO≌Rt△CEO(HL),
∴∠COD=∠COE,
∵OB平分∠ABC,OC平分∠ACB,
∴∠BOC=90°+A>90°是钝角三角形,
∴△BCO的外心在△BCO的外面,故C正确;
∵⊙O是Rt△ABC的内切圆,点D,E是切点,
∴OD⊥BC,OE⊥AC,
∴∠ODC=∠OEC=90°,
∴点O、D、C、E四点共圆,
∴四边形ODCE有外接圆,故D错误,
故选:D.
15.(3分)如图,在△ABC中,∠B=90°,AB=6cm,BC=7cm.点P从点B开始沿边BA向点A以2cm/s的速度移动,同时点Q从点C开始沿边CB向点B以1cm/s的速度移动,当其中一点到达终点时,另一点随即停止.当四边形APQC的面积为11cm2时,点P的运动时间为( )
A.1s B.1s或2.5s C.2s D.2s或5s
【分析】设当四边形APQC的面积为11cm2时,点P的运动时间为xs,由题意:四边形APQC的面积为11 cm2,列出一元二次方程,解方程,即可解决问题.
【解答】解:由题意得:PB=2xcm,CQ=xcm,
则BQ=BC﹣CQ=(7﹣x)cm,
设当四边形APQC的面积为11cm2时,点P的运动时间为xs,
由题意得:×6×7﹣ 2x(7﹣x)=11,
整理得:x2﹣7x+10=0,
解得:x1=2,x2=5(不符合题意舍去),
∴x=2,
即当四边形APQC的面积为11cm2时,点P的运动时间为2s,
故选:C.
16.(3分)若直线y=m(m为常数)与函数的图象恒有三个不同的交点,则m的取值范围是( )
A.0<m<2 B.0<m≤2 C.0<m<4 D.0<m≤4
【分析】根据已知解析式画出函数图象,进而得出常数m的取值范围.
【解答】解:如图所示:当x=2时,y=2,
故直线y=m(m为常数)与函数的图象恒有三个不同的交点,
则常数m的取值范围是:0<m<2.
故选:A.
二、填空题.(本大题有3个小题,每小题有2个空,每空2分,共12分.把答案写在题中横线上)
17.(4分)若点A(a﹣2,b+2)与点B(4,﹣3)关于原点对称.
(1)点A在第 二 象限;
(2)a﹣b的值为 ﹣3 .
【分析】两个点关于原点对称时,它们的横坐标互为相反数,纵坐标也互为相反数,直接利用关于原点对称点的性质得出a,b的值,进而得出答案.
【解答】解:(1)∵点A(a﹣2,b+2)与点B(4,﹣3)关于原点成中心对称,B在第四象限,
∴A在第二象限;
故答案为:二.
(2)由题意可知:
a﹣2=﹣4,b+2=3,
∴a=﹣2,b=1.
∴a﹣b=﹣2﹣1=﹣3.
故答案为:﹣3.
18.(4分)已知y与x成反比例,当x=﹣1时,y=﹣6.
(1)y与x的函数解析式为 ;
(2)若点A(a,﹣4),B(b,﹣8)都在该反比例函数的图象上,则a,b的大小关系是 b>a .
【分析】(1)首先设反比例函数解析式为y=(k≠0),再把x=﹣1,y=﹣6代入即可算出k的值,进而得到解析式;
(2)根据反比例函数的性质即可判断.
【解答】解:(1)设所求函数解析式为y=(k≠0),
由题意得:k=﹣1×(﹣6)=6,
故解析式为;
故答案为:;
(2)∵k=6>0,
∴反比例函数的图象在一、三象限,在每个象限y随x的增大而减小,
∵点A(a,﹣4),B(b,﹣8)都在该反比例函数的图象上,
∴点A(a,﹣4),B(b,﹣8)都在第三象限,
∵﹣4>﹣8,
∴b>a,
故答案为:b>a.
19.(4分)如图,已知在△ABC中,AB=AC=5,BC=8,点P在边BC上(点P与点B,C不重合),∠APF=∠B,射线PF与边AC交于点F,过点A作BC的平行线,交射线PF于点Q.
(1)若BP=2,则CF的长为 ;
(2)当△AFQ是等腰三角形时,BP的长为 5或 .
【分析】(1)由AB=AC得到∠B=∠C,又∠APF=∠B可得到∠BAP=∠CPF,故△ABP∽△PCF,从而有=,即可得到CF的长;
(2)分类讨论,①AF=FQ,②AQ=AF,③AQ=FQ,然后利用相似三角形的性质进行求解.
【解答】解:(1)∵AB=AC,
∴∠B=∠C,
∵∠B=∠APF,∠APF+∠FPC=∠B+∠BAP,
∴∠FPC=∠BAP,
∴△ABP∽△PCF,
∴=,
∵BP=2,BC=8,
∴CP=BC﹣BP=8﹣2=6,
∴=,
∴CF=;
故答案为:;
(2)①如图1,当AF=FQ时,∠FAQ=∠FQA,
∵AQ∥BC,
∴∠FQA=∠FPC,∠FAQ=∠C,
∵AB=AC,
∴∠B=∠C,
∴∠FQA=∠FPC=∠FAQ=∠C=∠B,
∴AB∥PQ,
∵∠APQ=∠B,
∴△APQ∽△ABC,
∴=,
∵AQ∥BC,AB∥PQ,
∴四边形ABPQ是平行四边形,
∴PQ=AB=5,AQ=BP,
∴=,
∴BP=;
②如图2,当AQ=AF时,∠AQF=∠AFQ,
∵∠AFQ=∠PFC,∠AQF=∠FPC,
∴∠CFP=∠CPF,
∴CP=CF,
由(1)得∠FPC=∠PAB,
∵∠B=∠C,
∴△BAP∽△CPF,
∴=,
∴AB=BP=5;
③如图3,当AQ=QF时,∠QAF=∠QFA,
∵∠QFA=∠PFC,∠QAF=∠C,
∴∠PFC=∠C,
∵∠C=∠B=∠APQ,
∴∠APQ=∠PFC,
∴AP∥CF,矛盾,舍去,
综上所述,BP的长为5或,
故答案为:5或.
三、解答题.(本大题共7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
20.(8分)用适当的方法解下列方程.
(1)x2﹣2x﹣4=0;
(2)(x﹣5)(x+2)=8.
【分析】(1)利用配方法得到(x﹣1)2=5,然后利用直接开平方法解方程;
(2)先把方程变形为x2﹣3x﹣18=0,然后利用因式分解法解方程.
【解答】解:(1)x2﹣2x﹣4=0,
x2﹣2x=4,
x2﹣2x+1=5,即(x﹣1)2=5,
∴x﹣1=±,
∴x1=1+,x2=1﹣;
(2)(x﹣5)(x+2)=8,
x2﹣3x﹣18=0,
(x﹣6)(x+3)=0,
∴x﹣6=0或x+3=0,
∴x1=6,x2=﹣3.
21.(9分)如图,在△ABC中,∠C=90°,AC=3,点D在边BC上,且tan∠CAD=.
(1)求cos∠CAD的值;
(2)若BD=2CD,求sinB的值.
【分析】(1)在Rt△ACD中,利用锐角三角函数的定义求出CD=2,从而利用勾股定理求出AD=,然后再利用锐角三角函数的定义进行计算即可解答;
(2)根据已知可得BC=3CD=6,然后在Rt△ABC中,利用勾股定理求出AB的长,从而利用锐角三角函数的定义进行计算即可解答.
【解答】解:(1)在Rt△ACD中,tan∠CAD=,AC=3,
∴CD=AC tan∠CAD=3×=2,
∴AD===,
∴cos∠CAD===,
∴cos∠CAD的值为;
(2)∵BD=2CD,CD=2,
∴BC=3CD=6,
在Rt△ABC中,根据勾股定理可得:AB===3,
∴sinB===,
∴sinB的值为.
22.(9分)某新冠疫苗接种点有4个完全相同的冷藏箱用来储存疫苗,同一冷藏箱里的疫苗都来自同一厂家,其有两箱储存A厂家的疫苗,另两箱分别储存B厂家和C厂家的疫苗.
(1)如果将4个箱子随机送往4个接种台,每个接种台接受一个箱子,那么1号台恰好收到A厂家疫苗的概率是 ;
(2)如果从中随机拿出两个箱子,送往1号和2号接种台,请用列表或画树状图的方法求拿出的两个冷藏箱里有A厂家疫苗的概率.
【分析】(1)根据有两箱储存A厂家的疫苗,4个箱子随机送往4个接种台,得出1号台恰好收到A厂家疫苗的概率;
(2)根据4个箱子随机拿出两个箱子,列树形图,从图中可知,共有12种等可能的结果,其中有A厂家疫苗的结果有10种,从而求出拿出的两个冷藏箱里有A厂家疫苗的概率.
【解答】解:(1)根据题意,得P1==,
故答案为:;
(2)树状图如图,
,
由树状图可知,共有12种等可能的结果,其中有A厂家疫苗的结果有10种,
∴P(拿出的两个冷藏箱里有A厂家疫苗)==,
答:拿出的两个冷藏箱里有A厂家疫苗的概率是.
23.(9分)如图,已知点A(a,2),B(﹣1,b)是直线y=2x﹣6与反比例函数y=图象的交点,且该直线与y轴交于点C.
(1)求该反比例函数的解析式;
(2)连接OA,OB,求△AOB的面积;
(3)根据图象,直接写出不等式2x﹣6的解集.
【分析】(1)由一次函数的解析式求得A、B的坐标,然后利用待定系数法即可求得反比例函数的解析式;
(2)由于直线AB与y轴交于点C,所以三角形AOB的面积是三角形AOC和三角形OCB的面积之和,依此列式计算即可;
(3)根据图象求解即可.
【解答】解:(1)∵点A(a,2),B(﹣1,b)是直线y=2x﹣6上的点,
∴2=2a﹣6,b=﹣2﹣6,
∴a=4,b=﹣8,
∴A(4,2),B(﹣1,﹣8),
把A的坐标代入y=得,2=,
∴m=8,
∴反比例函数的解析式为y=;
(2)∵直线AB与y轴交于点C,
∴当x=0时,y=﹣6.
∴点C(0,﹣6),
∴OC=6,
∴S△AOB=S△ACO+S△BCO=×4+=15;
(3)观察图象,不等式2x﹣6的解集﹣1≤x<0或x≥4.
24.(9分)如图,正方形ABCD的边长为4,动点P在边AB上从点B沿BA向点A运动(点P不与点A,B重合),连接PC.过点P作PE⊥PC,PE交AD于点Q.
(1)求证:△APQ∽△BCP;
(2)若S△APQ:S△BCP=1:16,求AQ的长度;
(3)连接CQ.试判断当点P运动到边AB的什么位置时,△PCQ∽△BCP?并说明理由.
【分析】(1)利用等角的余角相等得到∠AQP=∠BPC,再证明三角形相似即可;
(2)根据相似的性质可得==,设BP=x,则AP=4﹣x,求出x的值即可求AQ;
(3)根据△APQ∽△BCP,求出AQ=1,即可分别求出PQ=,PC=2,再由==,∠CPQ=∠B=90°,可得到△PCQ∽△BCP.
【解答】(1)证明:∵四边形ABCD是正方形,
∴∠A=∠B=90°,
∴∠APQ+∠AQP=90°,
∵PE⊥PC,
∴∠APQ+∠BPC=90°,
∴∠AQP=∠BPC,
∴△APQ∽△BCP;
(2)解:∵S△APQ:S△BCP=1:16,△APQ∽△BCP,
∴==,
设BP=x,则AP=4﹣x,
∴=,
解得x=3,
∴AQ=;
(3)解:当点P运动到边AB的中点时,△PCQ∽△BCP,理由如下:
∵P是AB的中点,
∴AP=BP=2,
∵△APQ∽△BCP,
∴=,即=,
∴AQ=1,
∴PQ=,PC=2,
∴==,
又∵∠CPQ=∠B=90°,
∴△PCQ∽△BCP.
25.(10分)如图1,已知∠ABC=60°,点O在射线BC上,且OB=4.以点O为圆心,r(r>0)为半径作⊙O,交直线BC于点D,E.
(1)当⊙O与∠ABC只有两个交点时,r的取值范围是 0<r<2或r>4 ;
(2)当时,将射线BA绕点B按顺时针方向旋转α(0°<α<180°).
①当α为多少时,射线BA与⊙O相切;
②如图2,射线BA与⊙O交于M,N两点,若MN=OB,求阴影部分的面积.
【分析】(1)根据题意,需要分两种情况:①在点D未到达点B前,圆O与射线BC有两个交点;②在点D到达点B后,圆O分别与射线BA,BC有一个交点,求出临界状态的r即可得出结论;
(2)①需要分两种情况:当射线BA在射线BC的上方与⊙O相切时,当射线BA在射线BC的下方与⊙O相切时,分别求出对应的α即可;
②连接OM,ON,过点O作OQ⊥MN于点Q由垂径定理可知,MQ=NQ=MN=2,进而根据三角形三边关系可得出∠MON=90°,再利用弓形的面积公式可得出结论.
【解答】解:(1)根据题意,需要分两种情况:①在点D未到达点B前,圆O与射线BC有两个交点;
当圆O与AB相切与点G,连接OG,则OG⊥AB,
∵∠ABC=60°,
∴∠BOG=30°,
∴BG=OB=2,OG=BG=2.
即此时r=2.
②在点D到达点B后,圆O分别与射线BA,BC有一个交点,
如图,当点D刚好于点B重合,
此时r=4,
结合图形可知,r的取值范围为:0<r<2或r>4;
(2)①如图,当射线BA在射线BC的上方与⊙O相切时,设切点为P,连接OP.
∵OB=4,OP=2,
∴sin∠ABC==,
∴∠ABC=45°,
∴α=60°﹣45°=15°.
如图,当射线BA在射线BC的下方与⊙O相切时,设切点为P,连接OP.
同理可得,∠ABC=45°,
∴α=60°+45°=105°.
综上所述,当α为15°或105°时,射线BA与⊙O相切;
②如图,连接OM,ON,过点O作OQ⊥MN于点Q,
∴MQ=NQ=MN=2.
∵OM=2,
∴sin∠MOQ==,
∴∠MOQ=45°,
∴∠MON=2∠MOQ=90°,
∴S阴影=﹣×(2)2=2π﹣4.
26.(12分)一小球M从斜坡OA上的点O处抛出,球的抛出路线是抛物线的一部分,建立如图所示的平面直角坐标系,斜坡可以用一次函数刻画.若小球到达最高点的坐标为(4,8).
(1)求抛物线的函数解析式(不写自变量x的取值范围);
(2)小球在斜坡上的落点A的垂直高度为 米;
(3)若要在斜坡OA上的点B处竖直立一个高4米的广告牌,点B的横坐标为2,请判断小球M能否飞过这个广告牌?通过计算说明理由;
(4)求小球M在飞行的过程中离斜坡OA的最大高度.
【分析】(1)设抛物线的表达式为y=a(x﹣4)2+8,把(0,0)代入即可得到答案;
(2)联立抛物线解析式和一次函数解析式,解方程组求出A点坐标即可;
(3)把x=2分别代入y=﹣(x﹣4)2+8和y=x,即可得到答案;
(4)根据二次函数的性质即可得到结论.
【解答】解:(1)∵小球到达的最高的点坐标为(4,8),
∴设抛物线的表达式为y=a(x﹣4)2+8,
把(0,0)代入得,0=a(0﹣4)2+8,
解得:a=﹣,
∴抛物线的表达式为y=﹣(x﹣4)2+8;
(2)联立方程组,
解得或,
∴A(7,),
∴小球在斜坡上的落点A的垂直高度为米,
故答案为:;
(3)当x=2时,y1=x=1,y2=﹣(x﹣4)2+8=6,
∵6﹣1>4,
∴小球M能飞过这棵树;
(4)小球M在飞行的过程中离斜坡OA的高度h=﹣(x﹣4)2+8﹣x=﹣(x﹣)2+,
∴小球M在飞行的过程中离斜坡OA的最大高度为 .
一、选择题.(本大题有16个小题,共42分.1~10小题各3分;11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(3分)抛物线y=x2+2x﹣3与y轴的交点坐标是( )
A.(0,﹣3) B.(﹣3,0) C.(0,2) D.(2,0)
2.(3分)已知在 Rt△ABC中,∠C=90°,cosA=,则∠B的度数为( )
A.30° B.45° C.60° D.无法确定
3.(3分)已知△ABC∽△DEF,相似比为,若△ABC的周长为3,则△DEF的周长为( )
A.1 B.3 C.9 D.27
4.(3分)如图,AB是⊙O的直径,CO⊥AB,点D在直径AB上方的⊙O上,连接BD,CD,则∠CDB的度数是( )
A.30° B.45° C.60° D.75°
5.(3分)三张质地、大小、背面完全相同的卡片上,正面分别画有圆、平行四边形和等边三角形三个图案.现把它们的正面向下随机摆放在桌面上,从中任意抽出一张,则抽出的卡片正面图案是中心对称图形的概率为( )
A. B. C. D.
6.(3分)如图是东西流向且河岸平行的一段河道,点A,B分别为两岸上一点,且点B在点A正南方向,由点B向正西方向走a米到达点C,此时测得点C在点A的南偏西50°方向上,则河宽AB的长为( )
A.atan50°米 B.米 C.米 D.米
7.(3分)关于抛物线y=﹣3(x﹣1)2+5,下列说法正确的是( )
A.开口向上
B.对称轴为直线x=﹣1
C.当x≥1时,y随x的增大而减小
D.该抛物线向上平移2个单位长度后可经过原点
8.(3分)如图中的两个三角形是以点P为位似中心的位似图形,则点P的坐标是( )
A.(0,﹣4) B.(4,﹣2) C.(3,﹣1) D.(0,0)
9.(3分)如图,将△ABC绕点A逆时针旋转88°得到△AB'C',若点B'恰好落到边BC上,则∠AB'C'的度数为( )
A.44° B.46° C.54° D.56°
10.(3分)在一个不透明的盒子中装有a个黑白颜色的球,小明又放入了5个红球,这些球大小相同.若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子,通过大量重复试验后,发现摸到红球的频率稳定在25%左右,则a的值大约为( )
A.15 B.20 C.25 D.30
11.(3分)⊙O的内接正方形和内接正六边形的边心距分别为a,b,则的值为( )
A. B. C. D.
12.(3分)关于x的一元二次方程x2+mx﹣m﹣2=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.实数根的个数由m的值确定
13.(3分)如图,矩形ABCD在平面直角坐标系中,点A,D分别在反比例函数和的图象上,点B,C在x轴上,若S矩形ABCD=4,则k的值为( )
A.12 B.7 C.﹣12 D.﹣7
14.(3分)如图,⊙O是Rt△ABC的内切圆,点D,E是切点,则下列说法不正确的是( )
A.CD=CE
B.∠ABO=45°
C.△BCO的外心在△BCO的外面
D.四边形ODCE没有外接圆
15.(3分)如图,在△ABC中,∠B=90°,AB=6cm,BC=7cm.点P从点B开始沿边BA向点A以2cm/s的速度移动,同时点Q从点C开始沿边CB向点B以1cm/s的速度移动,当其中一点到达终点时,另一点随即停止.当四边形APQC的面积为11cm2时,点P的运动时间为( )
A.1s B.1s或2.5s C.2s D.2s或5s
16.(3分)若直线y=m(m为常数)与函数的图象恒有三个不同的交点,则m的取值范围是( )
A.0<m<2 B.0<m≤2 C.0<m<4 D.0<m≤4
二、填空题.(本大题有3个小题,每小题有2个空,每空2分,共12分.把答案写在题中横线上)
17.(4分)若点A(a﹣2,b+2)与点B(4,﹣3)关于原点对称.
(1)点A在第 象限;
(2)a﹣b的值为 .
18.(4分)已知y与x成反比例,当x=﹣1时,y=﹣6.
(1)y与x的函数解析式为 ;
(2)若点A(a,﹣4),B(b,﹣8)都在该反比例函数的图象上,则a,b的大小关系是 .
19.(4分)如图,已知在△ABC中,AB=AC=5,BC=8,点P在边BC上(点P与点B,C不重合),∠APF=∠B,射线PF与边AC交于点F,过点A作BC的平行线,交射线PF于点Q.
(1)若BP=2,则CF的长为 ;
(2)当△AFQ是等腰三角形时,BP的长为 .
三、解答题.(本大题共7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
20.(8分)用适当的方法解下列方程.
(1)x2﹣2x﹣4=0;
(2)(x﹣5)(x+2)=8.
21.(9分)如图,在△ABC中,∠C=90°,AC=3,点D在边BC上,且tan∠CAD=.
(1)求cos∠CAD的值;
(2)若BD=2CD,求sinB的值.
22.(9分)某新冠疫苗接种点有4个完全相同的冷藏箱用来储存疫苗,同一冷藏箱里的疫苗都来自同一厂家,其有两箱储存A厂家的疫苗,另两箱分别储存B厂家和C厂家的疫苗.
(1)如果将4个箱子随机送往4个接种台,每个接种台接受一个箱子,那么1号台恰好收到A厂家疫苗的概率是 ;
(2)如果从中随机拿出两个箱子,送往1号和2号接种台,请用列表或画树状图的方法求拿出的两个冷藏箱里有A厂家疫苗的概率.
23.(9分)如图,已知点A(a,2),B(﹣1,b)是直线y=2x﹣6与反比例函数y=图象的交点,且该直线与y轴交于点C.
(1)求该反比例函数的解析式;
(2)连接OA,OB,求△AOB的面积;
(3)根据图象,直接写出不等式2x﹣6的解集.
24.(9分)如图,正方形ABCD的边长为4,动点P在边AB上从点B沿BA向点A运动(点P不与点A,B重合),连接PC.过点P作PE⊥PC,PE交AD于点Q.
(1)求证:△APQ∽△BCP;
(2)若S△APQ:S△BCP=1:16,求AQ的长度;
(3)连接CQ.试判断当点P运动到边AB的什么位置时,△PCQ∽△BCP?并说明理由.
25.(10分)如图1,已知∠ABC=60°,点O在射线BC上,且OB=4.以点O为圆心,r(r>0)为半径作⊙O,交直线BC于点D,E.
(1)当⊙O与∠ABC只有两个交点时,r的取值范围是 ;
(2)当时,将射线BA绕点B按顺时针方向旋转α(0°<α<180°).
①当α为多少时,射线BA与⊙O相切;
②如图2,射线BA与⊙O交于M,N两点,若MN=OB,求阴影部分的面积.
26.(12分)一小球M从斜坡OA上的点O处抛出,球的抛出路线是抛物线的一部分,建立如图所示的平面直角坐标系,斜坡可以用一次函数刻画.若小球到达最高点的坐标为(4,8).
(1)求抛物线的函数解析式(不写自变量x的取值范围);
(2)小球在斜坡上的落点A的垂直高度为 米;
(3)若要在斜坡OA上的点B处竖直立一个高4米的广告牌,点B的横坐标为2,请判断小球M能否飞过这个广告牌?通过计算说明理由;
(4)求小球M在飞行的过程中离斜坡OA的最大高度.
2021-2022学年河北省沧州市孟村县九年级(上)期末数学试卷
参考答案与试题解析
一、选择题.(本大题有16个小题,共42分.1~10小题各3分;11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(3分)抛物线y=x2+2x﹣3与y轴的交点坐标是( )
A.(0,﹣3) B.(﹣3,0) C.(0,2) D.(2,0)
【分析】令x=0,求出相应的y的值,即可得到抛物线y=x2+4x﹣1与y轴的交点坐标.
【解答】解:∵抛物线y=x2+2x﹣3,
∴当x=0时,y=﹣3,
即抛物线y=x2+2x﹣3与y轴的交点坐标是(0,﹣3),
故选:A.
2.(3分)已知在 Rt△ABC中,∠C=90°,cosA=,则∠B的度数为( )
A.30° B.45° C.60° D.无法确定
【分析】直接利用特殊角的三角函数值得出∠A的度数,进而利用直角三角形的性质得出答案.
【解答】解:在 Rt△ABC中,∠C=90°,
∵cosA=,
∴∠A=60°,
∴∠B的度数为:90°﹣60°=30°.
故选:A.
3.(3分)已知△ABC∽△DEF,相似比为,若△ABC的周长为3,则△DEF的周长为( )
A.1 B.3 C.9 D.27
【分析】根据相似三角形的性质得△ABC的周长:△DEF的周长=1:3,然后把△ABC的周长=3代入可计算出△DEF的周长.
【解答】解:∵△ABC与△DEF的相似比为1:3,
∴△ABC的周长:△DEF的周长=1:3,
∴△DEF的周长=3×3=9.
故选:C.
4.(3分)如图,AB是⊙O的直径,CO⊥AB,点D在直径AB上方的⊙O上,连接BD,CD,则∠CDB的度数是( )
A.30° B.45° C.60° D.75°
【分析】利用圆周角定理∠CDB==45°.
【解答】解:∵AB是⊙O的直径,CO⊥AB,
∴∠AOC=∠BOC=90°,
∴∠CDB===45°.
故选:B.
5.(3分)三张质地、大小、背面完全相同的卡片上,正面分别画有圆、平行四边形和等边三角形三个图案.现把它们的正面向下随机摆放在桌面上,从中任意抽出一张,则抽出的卡片正面图案是中心对称图形的概率为( )
A. B. C. D.
【分析】共有3个等可能的结果,抽出的卡片正面图案都是中心对称图形的结果有2个,再由概率公式求解即可.
【解答】解:圆、平行四边形和等边三角形三个图案是中心对称图形的是圆、平行四边形.从中任意抽出一张,抽出的卡片正面图案都是中心对称图形的结果有2个,
∴抽出的卡片正面图案都是中心对称图形的概率为,
故选:D.
6.(3分)如图是东西流向且河岸平行的一段河道,点A,B分别为两岸上一点,且点B在点A正南方向,由点B向正西方向走a米到达点C,此时测得点C在点A的南偏西50°方向上,则河宽AB的长为( )
A.atan50°米 B.米 C.米 D.米
【分析】根据正切的定义解答即可.
【解答】解:在Rt△ABC中,∠C=90°,∠BAC=50°,BC=a米,
∵tan∠BAC=,
∴AB==(米),
故选:D.
7.(3分)关于抛物线y=﹣3(x﹣1)2+5,下列说法正确的是( )
A.开口向上
B.对称轴为直线x=﹣1
C.当x≥1时,y随x的增大而减小
D.该抛物线向上平移2个单位长度后可经过原点
【分析】由二次函数顶点式解析式,根据二次函数的性质进行解答即可.
【解答】解:由抛物线解析式可得,
a<0,
∴开口向下,A错误;
对称轴x=1,B错误;
∴当x≥1时,y随x的增大而减小,C正确;
∵顶点坐标为(1,5),
∴该抛物线向上平移2个单位后顶点为(1,7),
∴平移后抛物线解析式为y=﹣3(x﹣1)2+7,
令x=0,则y=4≠0,
∴平移后抛物线不经过原点,
故D错误.
故选:C.
8.(3分)如图中的两个三角形是以点P为位似中心的位似图形,则点P的坐标是( )
A.(0,﹣4) B.(4,﹣2) C.(3,﹣1) D.(0,0)
【分析】根据位似变换的概念找出位似中心.
【解答】解:对应点所连线段所在的直线交于(4,﹣2)
∴点P的坐标为(4,﹣2),
故选:B.
9.(3分)如图,将△ABC绕点A逆时针旋转88°得到△AB'C',若点B'恰好落到边BC上,则∠AB'C'的度数为( )
A.44° B.46° C.54° D.56°
【分析】根据旋转的性质可求得AB=AB′,∠AB′C′的度数.
【解答】解:由旋转的性质可知:AB=AB′,旋转角∠BAB′=88°,
∴∠B=∠AB′C′,
∵AB=AB′,
∴∠B=∠BB′A=46°,
∴∠AB'C'=46°.
故选:B.
10.(3分)在一个不透明的盒子中装有a个黑白颜色的球,小明又放入了5个红球,这些球大小相同.若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子,通过大量重复试验后,发现摸到红球的频率稳定在25%左右,则a的值大约为( )
A.15 B.20 C.25 D.30
【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手,列出方程求解.
【解答】解:由题意可得,×100%=25%,
解得,a=15,
经检验:a=15是原分式方程的解,
所以a=15,
故选:A.
11.(3分)⊙O的内接正方形和内接正六边形的边心距分别为a,b,则的值为( )
A. B. C. D.
【分析】设⊙O的半径为R,如图,连接OB,OC,根据正六边形的性质得到∠BOC=60°,求得OB=OC=BC=R,根据勾股定理得到OM==,如图,连接OB,OC,根据正方形的性质得到∠BOC=90°,求得BC=OB=R,根据等腰直角三角形的性质得到ON=BC=R,于是得到结论.
【解答】解:设⊙O的半径为R,
如图,连接OB,OC,
∵多边形ABCDEF是正六边形,
∴∠BOC=60°,
∴OB=OC=BC=R,
∵OM⊥BC,
∴BM=BC=,
∴OM==,
如图,连接OB,OC,
∵四边形ABCD是正方形,
∴∠BOC=90°,
∴BC=OB=R,
∵ON⊥BC,
∴ON=BC=R,
∴==,
故选:D.
12.(3分)关于x的一元二次方程x2+mx﹣m﹣2=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.实数根的个数由m的值确定
【分析】先计算判别式的值,再配方得到Δ=(m+2)2+4>0,从而可判断方程根的情况.
【解答】解:∵Δ=m2﹣4(﹣m﹣2)
=m2+4m+8
=(m+2)2+4>0,
∴方程有两个不相等的实数根.
故选:A.
13.(3分)如图,矩形ABCD在平面直角坐标系中,点A,D分别在反比例函数和的图象上,点B,C在x轴上,若S矩形ABCD=4,则k的值为( )
A.12 B.7 C.﹣12 D.﹣7
【分析】延长AD,交y轴于E,如图,利用矩形的性质得AE∥x轴,AB⊥x轴,DC⊥x轴,则利用反比例函数的比例系数k的几何意义得到S矩形CDEO=|﹣3|=3,S矩形ABOE=|k|,进而得出|k|=3+4=7,即可求出k=﹣7.
【解答】解:延长AD,交y轴于E,如图,
∵四边形ABCD为矩形,
∴AE∥x轴,AB⊥x轴,DC⊥x轴,
∵点A,D分别在反比例函数和的图象上,点B,C在x轴上,
∴S矩形CDEO=|﹣3|=3,S矩形ABOE=|k|,
∵S矩形ABCD=4,
∴|k|=3+4=7,
∵k<0.
∴k=﹣7.
故选:D.
14.(3分)如图,⊙O是Rt△ABC的内切圆,点D,E是切点,则下列说法不正确的是( )
A.CD=CE
B.∠ABO=45°
C.△BCO的外心在△BCO的外面
D.四边形ODCE没有外接圆
【分析】根据三角形内切圆的性质得到OC平分∠ACB,OD⊥BC,OE⊥AC,根据角平分线的性质得到CD=CE,故A正确;根据角平分线的定义得到∠ABO=∠CBO==45°,故B正确;根据全等三角形的性质得到∠COD=∠COE,根据三角形的内角和定理得到∠BOC=90°+A>90°是钝角三角形,推出△BCO的外心在△BCO的外面,故C正确;推出点O、D、C、E四点共圆,得到四边形ODCE有外接圆,故D错误.
【解答】解:∵⊙O是Rt△ABC的内切圆,
∴OC平分∠ACB,OD⊥BC,OE⊥AC,
∴CD=CE,故A正确;
∵⊙O是Rt△ABC的内切圆,
∴OB平分∠ABC,
∵∠ABC=90°,
∴∠ABO=∠CBO==45°,故B正确;
∵OD⊥BC,
∴∠BOD=45°,
在Rt△CDO与Rt△CEO中,
,
∴Rt△CDO≌Rt△CEO(HL),
∴∠COD=∠COE,
∵OB平分∠ABC,OC平分∠ACB,
∴∠BOC=90°+A>90°是钝角三角形,
∴△BCO的外心在△BCO的外面,故C正确;
∵⊙O是Rt△ABC的内切圆,点D,E是切点,
∴OD⊥BC,OE⊥AC,
∴∠ODC=∠OEC=90°,
∴点O、D、C、E四点共圆,
∴四边形ODCE有外接圆,故D错误,
故选:D.
15.(3分)如图,在△ABC中,∠B=90°,AB=6cm,BC=7cm.点P从点B开始沿边BA向点A以2cm/s的速度移动,同时点Q从点C开始沿边CB向点B以1cm/s的速度移动,当其中一点到达终点时,另一点随即停止.当四边形APQC的面积为11cm2时,点P的运动时间为( )
A.1s B.1s或2.5s C.2s D.2s或5s
【分析】设当四边形APQC的面积为11cm2时,点P的运动时间为xs,由题意:四边形APQC的面积为11 cm2,列出一元二次方程,解方程,即可解决问题.
【解答】解:由题意得:PB=2xcm,CQ=xcm,
则BQ=BC﹣CQ=(7﹣x)cm,
设当四边形APQC的面积为11cm2时,点P的运动时间为xs,
由题意得:×6×7﹣ 2x(7﹣x)=11,
整理得:x2﹣7x+10=0,
解得:x1=2,x2=5(不符合题意舍去),
∴x=2,
即当四边形APQC的面积为11cm2时,点P的运动时间为2s,
故选:C.
16.(3分)若直线y=m(m为常数)与函数的图象恒有三个不同的交点,则m的取值范围是( )
A.0<m<2 B.0<m≤2 C.0<m<4 D.0<m≤4
【分析】根据已知解析式画出函数图象,进而得出常数m的取值范围.
【解答】解:如图所示:当x=2时,y=2,
故直线y=m(m为常数)与函数的图象恒有三个不同的交点,
则常数m的取值范围是:0<m<2.
故选:A.
二、填空题.(本大题有3个小题,每小题有2个空,每空2分,共12分.把答案写在题中横线上)
17.(4分)若点A(a﹣2,b+2)与点B(4,﹣3)关于原点对称.
(1)点A在第 二 象限;
(2)a﹣b的值为 ﹣3 .
【分析】两个点关于原点对称时,它们的横坐标互为相反数,纵坐标也互为相反数,直接利用关于原点对称点的性质得出a,b的值,进而得出答案.
【解答】解:(1)∵点A(a﹣2,b+2)与点B(4,﹣3)关于原点成中心对称,B在第四象限,
∴A在第二象限;
故答案为:二.
(2)由题意可知:
a﹣2=﹣4,b+2=3,
∴a=﹣2,b=1.
∴a﹣b=﹣2﹣1=﹣3.
故答案为:﹣3.
18.(4分)已知y与x成反比例,当x=﹣1时,y=﹣6.
(1)y与x的函数解析式为 ;
(2)若点A(a,﹣4),B(b,﹣8)都在该反比例函数的图象上,则a,b的大小关系是 b>a .
【分析】(1)首先设反比例函数解析式为y=(k≠0),再把x=﹣1,y=﹣6代入即可算出k的值,进而得到解析式;
(2)根据反比例函数的性质即可判断.
【解答】解:(1)设所求函数解析式为y=(k≠0),
由题意得:k=﹣1×(﹣6)=6,
故解析式为;
故答案为:;
(2)∵k=6>0,
∴反比例函数的图象在一、三象限,在每个象限y随x的增大而减小,
∵点A(a,﹣4),B(b,﹣8)都在该反比例函数的图象上,
∴点A(a,﹣4),B(b,﹣8)都在第三象限,
∵﹣4>﹣8,
∴b>a,
故答案为:b>a.
19.(4分)如图,已知在△ABC中,AB=AC=5,BC=8,点P在边BC上(点P与点B,C不重合),∠APF=∠B,射线PF与边AC交于点F,过点A作BC的平行线,交射线PF于点Q.
(1)若BP=2,则CF的长为 ;
(2)当△AFQ是等腰三角形时,BP的长为 5或 .
【分析】(1)由AB=AC得到∠B=∠C,又∠APF=∠B可得到∠BAP=∠CPF,故△ABP∽△PCF,从而有=,即可得到CF的长;
(2)分类讨论,①AF=FQ,②AQ=AF,③AQ=FQ,然后利用相似三角形的性质进行求解.
【解答】解:(1)∵AB=AC,
∴∠B=∠C,
∵∠B=∠APF,∠APF+∠FPC=∠B+∠BAP,
∴∠FPC=∠BAP,
∴△ABP∽△PCF,
∴=,
∵BP=2,BC=8,
∴CP=BC﹣BP=8﹣2=6,
∴=,
∴CF=;
故答案为:;
(2)①如图1,当AF=FQ时,∠FAQ=∠FQA,
∵AQ∥BC,
∴∠FQA=∠FPC,∠FAQ=∠C,
∵AB=AC,
∴∠B=∠C,
∴∠FQA=∠FPC=∠FAQ=∠C=∠B,
∴AB∥PQ,
∵∠APQ=∠B,
∴△APQ∽△ABC,
∴=,
∵AQ∥BC,AB∥PQ,
∴四边形ABPQ是平行四边形,
∴PQ=AB=5,AQ=BP,
∴=,
∴BP=;
②如图2,当AQ=AF时,∠AQF=∠AFQ,
∵∠AFQ=∠PFC,∠AQF=∠FPC,
∴∠CFP=∠CPF,
∴CP=CF,
由(1)得∠FPC=∠PAB,
∵∠B=∠C,
∴△BAP∽△CPF,
∴=,
∴AB=BP=5;
③如图3,当AQ=QF时,∠QAF=∠QFA,
∵∠QFA=∠PFC,∠QAF=∠C,
∴∠PFC=∠C,
∵∠C=∠B=∠APQ,
∴∠APQ=∠PFC,
∴AP∥CF,矛盾,舍去,
综上所述,BP的长为5或,
故答案为:5或.
三、解答题.(本大题共7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
20.(8分)用适当的方法解下列方程.
(1)x2﹣2x﹣4=0;
(2)(x﹣5)(x+2)=8.
【分析】(1)利用配方法得到(x﹣1)2=5,然后利用直接开平方法解方程;
(2)先把方程变形为x2﹣3x﹣18=0,然后利用因式分解法解方程.
【解答】解:(1)x2﹣2x﹣4=0,
x2﹣2x=4,
x2﹣2x+1=5,即(x﹣1)2=5,
∴x﹣1=±,
∴x1=1+,x2=1﹣;
(2)(x﹣5)(x+2)=8,
x2﹣3x﹣18=0,
(x﹣6)(x+3)=0,
∴x﹣6=0或x+3=0,
∴x1=6,x2=﹣3.
21.(9分)如图,在△ABC中,∠C=90°,AC=3,点D在边BC上,且tan∠CAD=.
(1)求cos∠CAD的值;
(2)若BD=2CD,求sinB的值.
【分析】(1)在Rt△ACD中,利用锐角三角函数的定义求出CD=2,从而利用勾股定理求出AD=,然后再利用锐角三角函数的定义进行计算即可解答;
(2)根据已知可得BC=3CD=6,然后在Rt△ABC中,利用勾股定理求出AB的长,从而利用锐角三角函数的定义进行计算即可解答.
【解答】解:(1)在Rt△ACD中,tan∠CAD=,AC=3,
∴CD=AC tan∠CAD=3×=2,
∴AD===,
∴cos∠CAD===,
∴cos∠CAD的值为;
(2)∵BD=2CD,CD=2,
∴BC=3CD=6,
在Rt△ABC中,根据勾股定理可得:AB===3,
∴sinB===,
∴sinB的值为.
22.(9分)某新冠疫苗接种点有4个完全相同的冷藏箱用来储存疫苗,同一冷藏箱里的疫苗都来自同一厂家,其有两箱储存A厂家的疫苗,另两箱分别储存B厂家和C厂家的疫苗.
(1)如果将4个箱子随机送往4个接种台,每个接种台接受一个箱子,那么1号台恰好收到A厂家疫苗的概率是 ;
(2)如果从中随机拿出两个箱子,送往1号和2号接种台,请用列表或画树状图的方法求拿出的两个冷藏箱里有A厂家疫苗的概率.
【分析】(1)根据有两箱储存A厂家的疫苗,4个箱子随机送往4个接种台,得出1号台恰好收到A厂家疫苗的概率;
(2)根据4个箱子随机拿出两个箱子,列树形图,从图中可知,共有12种等可能的结果,其中有A厂家疫苗的结果有10种,从而求出拿出的两个冷藏箱里有A厂家疫苗的概率.
【解答】解:(1)根据题意,得P1==,
故答案为:;
(2)树状图如图,
,
由树状图可知,共有12种等可能的结果,其中有A厂家疫苗的结果有10种,
∴P(拿出的两个冷藏箱里有A厂家疫苗)==,
答:拿出的两个冷藏箱里有A厂家疫苗的概率是.
23.(9分)如图,已知点A(a,2),B(﹣1,b)是直线y=2x﹣6与反比例函数y=图象的交点,且该直线与y轴交于点C.
(1)求该反比例函数的解析式;
(2)连接OA,OB,求△AOB的面积;
(3)根据图象,直接写出不等式2x﹣6的解集.
【分析】(1)由一次函数的解析式求得A、B的坐标,然后利用待定系数法即可求得反比例函数的解析式;
(2)由于直线AB与y轴交于点C,所以三角形AOB的面积是三角形AOC和三角形OCB的面积之和,依此列式计算即可;
(3)根据图象求解即可.
【解答】解:(1)∵点A(a,2),B(﹣1,b)是直线y=2x﹣6上的点,
∴2=2a﹣6,b=﹣2﹣6,
∴a=4,b=﹣8,
∴A(4,2),B(﹣1,﹣8),
把A的坐标代入y=得,2=,
∴m=8,
∴反比例函数的解析式为y=;
(2)∵直线AB与y轴交于点C,
∴当x=0时,y=﹣6.
∴点C(0,﹣6),
∴OC=6,
∴S△AOB=S△ACO+S△BCO=×4+=15;
(3)观察图象,不等式2x﹣6的解集﹣1≤x<0或x≥4.
24.(9分)如图,正方形ABCD的边长为4,动点P在边AB上从点B沿BA向点A运动(点P不与点A,B重合),连接PC.过点P作PE⊥PC,PE交AD于点Q.
(1)求证:△APQ∽△BCP;
(2)若S△APQ:S△BCP=1:16,求AQ的长度;
(3)连接CQ.试判断当点P运动到边AB的什么位置时,△PCQ∽△BCP?并说明理由.
【分析】(1)利用等角的余角相等得到∠AQP=∠BPC,再证明三角形相似即可;
(2)根据相似的性质可得==,设BP=x,则AP=4﹣x,求出x的值即可求AQ;
(3)根据△APQ∽△BCP,求出AQ=1,即可分别求出PQ=,PC=2,再由==,∠CPQ=∠B=90°,可得到△PCQ∽△BCP.
【解答】(1)证明:∵四边形ABCD是正方形,
∴∠A=∠B=90°,
∴∠APQ+∠AQP=90°,
∵PE⊥PC,
∴∠APQ+∠BPC=90°,
∴∠AQP=∠BPC,
∴△APQ∽△BCP;
(2)解:∵S△APQ:S△BCP=1:16,△APQ∽△BCP,
∴==,
设BP=x,则AP=4﹣x,
∴=,
解得x=3,
∴AQ=;
(3)解:当点P运动到边AB的中点时,△PCQ∽△BCP,理由如下:
∵P是AB的中点,
∴AP=BP=2,
∵△APQ∽△BCP,
∴=,即=,
∴AQ=1,
∴PQ=,PC=2,
∴==,
又∵∠CPQ=∠B=90°,
∴△PCQ∽△BCP.
25.(10分)如图1,已知∠ABC=60°,点O在射线BC上,且OB=4.以点O为圆心,r(r>0)为半径作⊙O,交直线BC于点D,E.
(1)当⊙O与∠ABC只有两个交点时,r的取值范围是 0<r<2或r>4 ;
(2)当时,将射线BA绕点B按顺时针方向旋转α(0°<α<180°).
①当α为多少时,射线BA与⊙O相切;
②如图2,射线BA与⊙O交于M,N两点,若MN=OB,求阴影部分的面积.
【分析】(1)根据题意,需要分两种情况:①在点D未到达点B前,圆O与射线BC有两个交点;②在点D到达点B后,圆O分别与射线BA,BC有一个交点,求出临界状态的r即可得出结论;
(2)①需要分两种情况:当射线BA在射线BC的上方与⊙O相切时,当射线BA在射线BC的下方与⊙O相切时,分别求出对应的α即可;
②连接OM,ON,过点O作OQ⊥MN于点Q由垂径定理可知,MQ=NQ=MN=2,进而根据三角形三边关系可得出∠MON=90°,再利用弓形的面积公式可得出结论.
【解答】解:(1)根据题意,需要分两种情况:①在点D未到达点B前,圆O与射线BC有两个交点;
当圆O与AB相切与点G,连接OG,则OG⊥AB,
∵∠ABC=60°,
∴∠BOG=30°,
∴BG=OB=2,OG=BG=2.
即此时r=2.
②在点D到达点B后,圆O分别与射线BA,BC有一个交点,
如图,当点D刚好于点B重合,
此时r=4,
结合图形可知,r的取值范围为:0<r<2或r>4;
(2)①如图,当射线BA在射线BC的上方与⊙O相切时,设切点为P,连接OP.
∵OB=4,OP=2,
∴sin∠ABC==,
∴∠ABC=45°,
∴α=60°﹣45°=15°.
如图,当射线BA在射线BC的下方与⊙O相切时,设切点为P,连接OP.
同理可得,∠ABC=45°,
∴α=60°+45°=105°.
综上所述,当α为15°或105°时,射线BA与⊙O相切;
②如图,连接OM,ON,过点O作OQ⊥MN于点Q,
∴MQ=NQ=MN=2.
∵OM=2,
∴sin∠MOQ==,
∴∠MOQ=45°,
∴∠MON=2∠MOQ=90°,
∴S阴影=﹣×(2)2=2π﹣4.
26.(12分)一小球M从斜坡OA上的点O处抛出,球的抛出路线是抛物线的一部分,建立如图所示的平面直角坐标系,斜坡可以用一次函数刻画.若小球到达最高点的坐标为(4,8).
(1)求抛物线的函数解析式(不写自变量x的取值范围);
(2)小球在斜坡上的落点A的垂直高度为 米;
(3)若要在斜坡OA上的点B处竖直立一个高4米的广告牌,点B的横坐标为2,请判断小球M能否飞过这个广告牌?通过计算说明理由;
(4)求小球M在飞行的过程中离斜坡OA的最大高度.
【分析】(1)设抛物线的表达式为y=a(x﹣4)2+8,把(0,0)代入即可得到答案;
(2)联立抛物线解析式和一次函数解析式,解方程组求出A点坐标即可;
(3)把x=2分别代入y=﹣(x﹣4)2+8和y=x,即可得到答案;
(4)根据二次函数的性质即可得到结论.
【解答】解:(1)∵小球到达的最高的点坐标为(4,8),
∴设抛物线的表达式为y=a(x﹣4)2+8,
把(0,0)代入得,0=a(0﹣4)2+8,
解得:a=﹣,
∴抛物线的表达式为y=﹣(x﹣4)2+8;
(2)联立方程组,
解得或,
∴A(7,),
∴小球在斜坡上的落点A的垂直高度为米,
故答案为:;
(3)当x=2时,y1=x=1,y2=﹣(x﹣4)2+8=6,
∵6﹣1>4,
∴小球M能飞过这棵树;
(4)小球M在飞行的过程中离斜坡OA的高度h=﹣(x﹣4)2+8﹣x=﹣(x﹣)2+,
∴小球M在飞行的过程中离斜坡OA的最大高度为 .
同课章节目录
