浙教版2022学年九上科学期末复习课件六:杠杆及其应用(课件 25张ppt)
文档属性
| 名称 | 浙教版2022学年九上科学期末复习课件六:杠杆及其应用(课件 25张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2022-12-20 19:01:41 | ||
图片预览


文档简介
(共25张PPT)
浙教版 科学(初中)
九上期末复习课(六)
杠杆及其应用
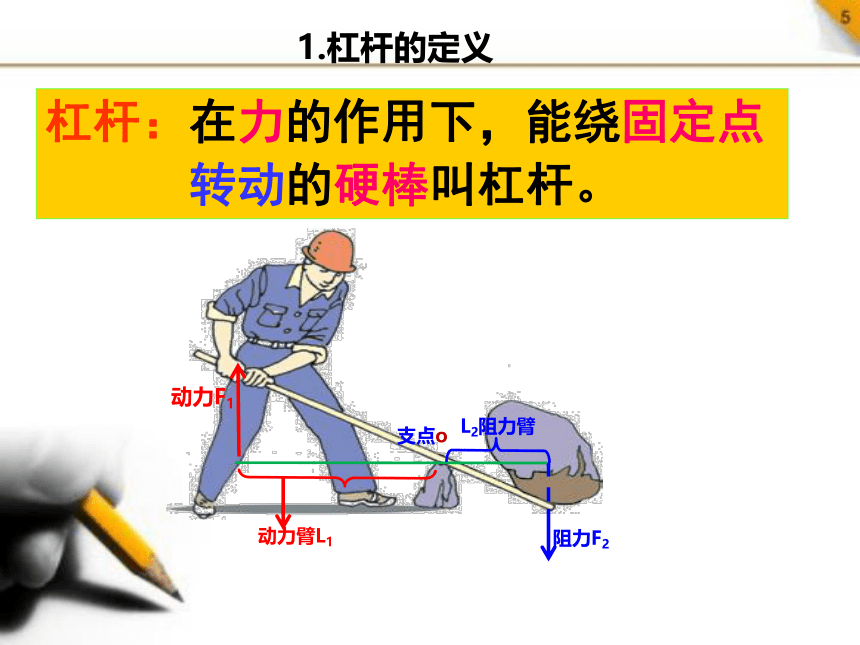
杠杆:在力的作用下,能绕固定点
转动的硬棒叫杠杆。
1.杠杆的定义
支点o
动力臂L1
L2阻力臂
阻力F2
动力F1
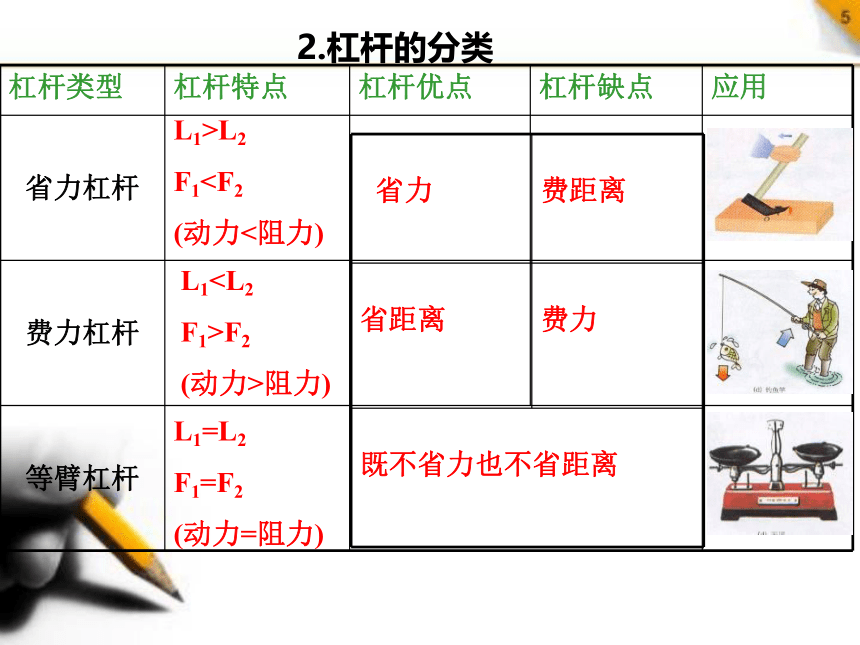
杠杆类型 杠杆特点 杠杆优点 杠杆缺点 应用
省力杠杆
费力杠杆
等臂杠杆
L1>L2
F1(动力<阻力)
省力
费距离
省距离
费力
既不省力也不省距离
L1F1>F2
(动力>阻力)
L1=L2
F1=F2
(动力=阻力)
2.杠杆的分类
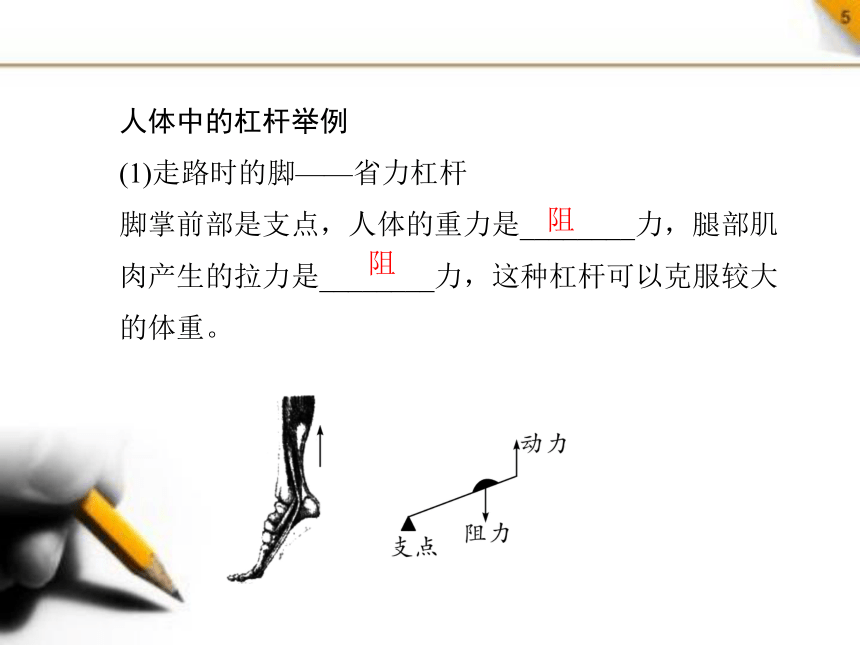
人体中的杠杆举例
(1)走路时的脚——省力杠杆
脚掌前部是支点,人体的重力是________力,腿部肌肉产生的拉力是________力,这种杠杆可以克服较大的体重。
阻
阻
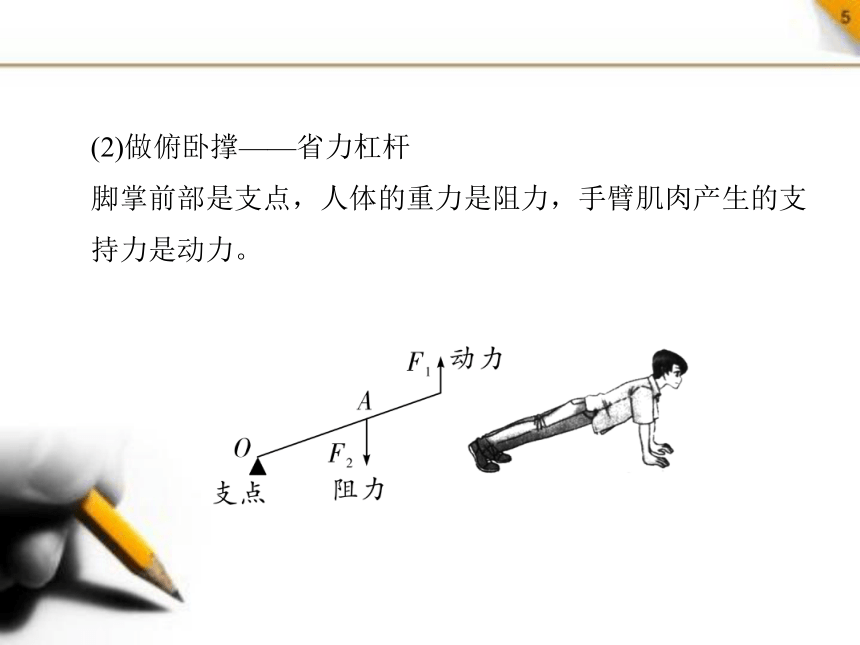
(2)做俯卧撑——省力杠杆
脚掌前部是支点,人体的重力是阻力,手臂肌肉产生的支持力是动力。
(3)仰卧起坐
仰卧起坐(腿部不动,用腹肌使整个上身起来):支点是臀部与支持面的接触点,阻力是上半身的重力,动力是腹肌肌肉产生的拉力,动力臂小于阻力臂,是费力杠杆。
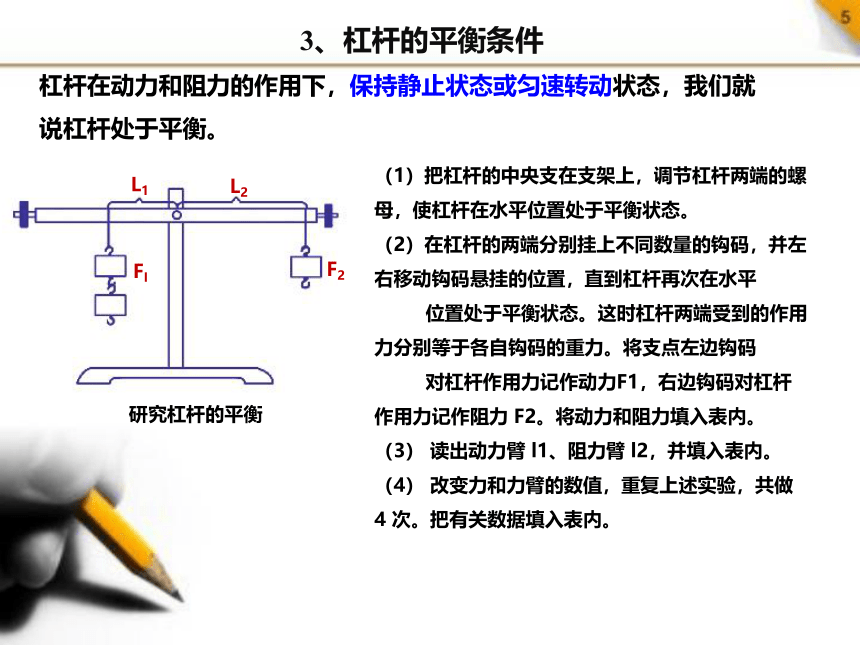
3、杠杆的平衡条件
杠杆在动力和阻力的作用下,保持静止状态或匀速转动状态,我们就说杠杆处于平衡。
L1
L2
FI
F2
研究杠杆的平衡
(1)把杠杆的中央支在支架上,调节杠杆两端的螺母,使杠杆在水平位置处于平衡状态。
(2)在杠杆的两端分别挂上不同数量的钩码,并左右移动钩码悬挂的位置,直到杠杆再次在水平
位置处于平衡状态。这时杠杆两端受到的作用力分别等于各自钩码的重力。将支点左边钩码
对杠杆作用力记作动力F1,右边钩码对杠杆作用力记作阻力 F2。将动力和阻力填入表内。
(3) 读出动力臂 l1、阻力臂 l2,并填入表内。
(4) 改变力和力臂的数值,重复上述实验,共做 4 次。把有关数据填入表内。
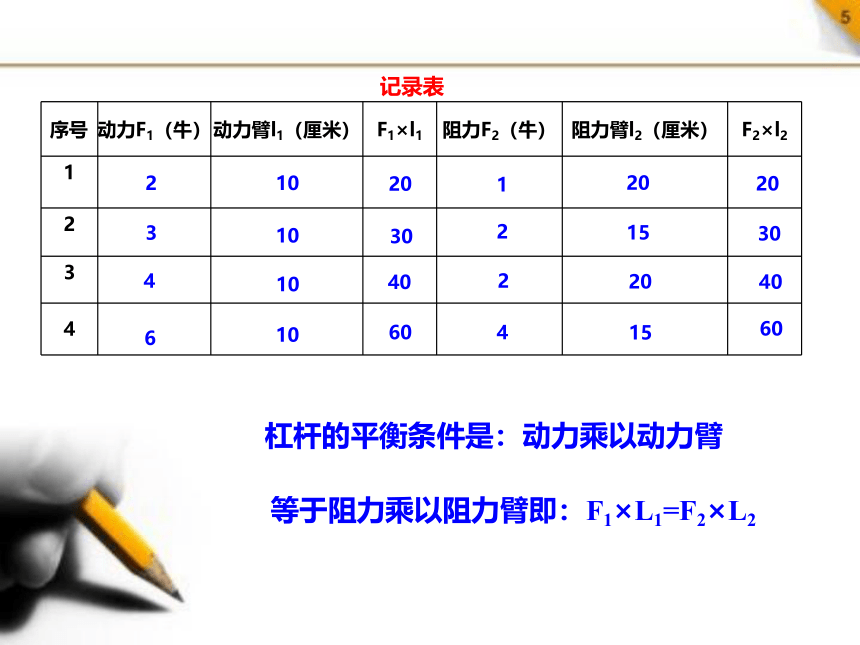
序号 动力F1(牛) 动力臂l1(厘米) F1×l1 阻力F2(牛) 阻力臂l2(厘米) F2×l2
1
2
3
4
3
10
2
15
4
20
2
10
6
10
4
15
2
20
10
1
20
30
40
60
20
30
40
60
记录表
杠杆的平衡条件是:动力乘以动力臂
等于阻力乘以阻力臂即:F1×L1=F2×L2
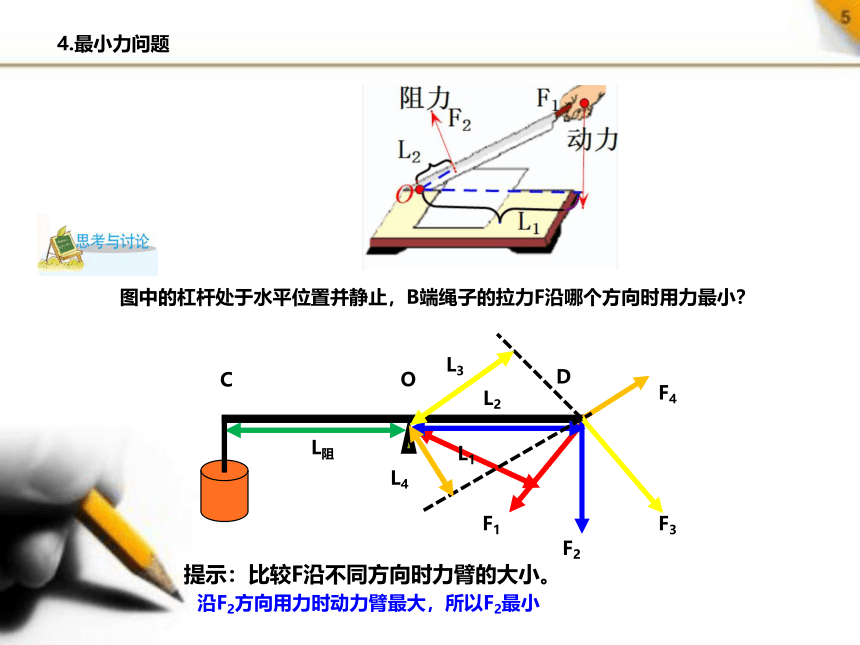
4.最小力问题
图中的杠杆处于水平位置并静止,B端绳子的拉力F沿哪个方向时用力最小?
L阻
L1
F1
F2
F4
F3
C
D
O
沿F2方向用力时动力臂最大,所以F2最小
L2
L3
L4
提示:比较F沿不同方向时力臂的大小。
F阻一般是不能改变的。
由杠杆平衡条件得:F动×L动=F阻×L阻
减小动力的方法:
1、减小阻力臂L阻
2、增大动力臂L动
通过对省力杠杆和费力杠杆的进一步分析,可以发现:
使用省力杠杆虽然省力,但是动力移动的距离比阻力移动的距离大。
而使用费力杠杆虽然费力,但是动力移动的距离比阻力移动的距离小。
基础过关
1、如图所示的杠杆中,O是支点,在B端挂一个重物,为使杠杆水平平衡,要在A端加一个力,下列说法中正确的是( )
A.在水平方向用力F1最小
B.在竖直方向用力F2最小
C.在跟OA连线垂直的方向F3最小
D.在各个方向上用力一样大
C
基础过关
2. 小金将长为0.6米、质量可忽略不计的木棒搁在肩上,棒的后端A挂一个40牛的物体,肩上支点O离后端A为0.2米,他用手压住前端B使木棒保持水平平衡,如图所示,小金的质量为50千克,则此时手压木棒的力大小为______牛,肩对木棒的支持力大小为________牛,人对地面的压力大小为________牛(g=10牛/千克)。
20
60
540
基础过关
3.如图所示,将长为1.2米的轻质木棒平放在水平方形台面上,左右两端点分别为A、B,它们距台面边缘处的距离均为0.3米。在A端挂一个重为30牛的物体,在B端挂一个重为G的物体。
(1)若G=30牛,台面受到木棒的压力为________牛。
(2)若要使木棒右端下沉,B端挂的物体至少要大于________牛。
(3)若B端挂物体后,木棒仍在水平台面上静止,则G的取值范围为________牛。
60
90
10~90
基础过关
4.在“探究杠杆的平衡条件”实验中:
(1)实验前调节杠杆在水平位置平衡,目的是____________________________.
(2)通过多次实验得出表格数据:
方便直接在杠杆上读出力臂
次数 F1/N l1/cm F2/N l2/cm
1 2 2 1 4
2 2 4 1 8
3 2 6 1 12
4 1 16 2 8
5 2 10 1 20
6 3 8 2 12
基础过关
分析1、2、3次实验数据,可以发现实验中存在的问题是:没有改变________的大小.
(3)分析4、5、6次实验数据,得出杠杆的平衡条件是____________(用字母表示)
(4)如图甲所示是某次实验中的情形,把图中杠杆
两侧的钩码各取下一个,为使杠杆再次在水平位
置平衡,应将左侧钩码向________移动一个格同
时右侧钩码向________移动一个格.(选填“左”
或“右”)
例题图甲
力
F1l1=F2l2
右
左
基础过关
(5)实验前在调节杠杆平衡时,若杠杆静止时左端高右端低,此时杠杆处于________(选填“平衡”或“非平衡”)状态,此时应将杠杆两端的平衡螺母向________(选填“左”或“右”)调节.
(6)实验中改变钩码质量和力臂进行多次实验的目的是_____________________.
平衡
左
使得出的结论具有普遍性
基础过关
拓展设问题图乙
(7)将杠杆一侧的钩码换成弹簧测力计,先后进行如图乙所示的两次实验,第一次弹簧测力计竖直向下拉,示数为F1;第二次弹
簧测力计斜着拉,示数为F2.若两次杠杆保持水平
平衡,则当弹簧测力计由第一种位置转至第二种
位置的过程中,弹簧测力计的示数F1________(选
填“>”“<”或“=”)F2.
(8)进行完实验后,探讨以下三个因素对实验
的影响:①支架自身的重力足够大;②单个钩码的重力不完全相等;③杠杆与转轴之间的摩擦偏大.其中不会带来实验误差的是________(填序号).
<
①
基础过关
(9)小明同学所在的实验小组在完成规定实验后,他们想进一步研究,如果杠杆受到F2、F3两个阻力,结果会怎样?通过实验,
他们得到了如图丙所示的结果,根据这个结果,
可以初步得出,在这种情况下杠杆的平衡条件
为:F1L1=____________(用F2、F3、L2、L3表示).
相比图乙所示的方法,利用这种方法进行探究
的不足之处是____________________________
________________________________________.
图丙
F2L2+F3L3
杠杆右端力臂数量太多,不便于得出实验结论
提高训练
1、衣服夹是一种常用物品,如图所示,给出了用手捏开和夹住物品时的两种情况。下列说法中,正确的是( )
A.当用手将其捏开时,它是费力杠杆
B.当用其夹住物品时,它是费力杠杆
C.无论用手将其捏开还是夹住物品时,它都是费力杠杆
D.无论用手将其捏开还是夹住物品时,它都是省力杠杆
B
提高训练
2、如图所示,足够长的杠杆上放着质量不相等(m1>m2)的两个球,杠杆在水平位置平衡,若两球以相同速度同时向远离支点的方向运动相等的时间,则杠杆 ( )
A.仍平衡
B.大球那端下沉
C.小球那端下沉
D.无法确定
B
提高训练
3、如图所示,某同学发现了一个金属块。他想知道它的重力和密度。他手中只有一只量程较小的弹簧秤,当他用此弹簧秤测量此金属块的重力时,发现已超过弹簧秤的最大量程,于是他设计了如图所示的装置。OA∶AB=1∶3,用弹簧秤在B点施加一个竖直向上的力,当OB杠杆水平静止时,弹簧秤读数为1.8 N,当向容器中加水,金属块浸没于水中后,弹簧秤读数为1.2 N,则金属块受到的重力是__________N;密度是_____________kg/m3。
7.2
3×103
提高训练
4.如图甲,有一轻质杆,左右各挂由同种金属制成、质量分别为m1和m2(m1>m2)的实心物块后恰好水平平衡。
(1)求左右悬挂点到支点O的距离L1与L2之比。
(2)将两物分别浸没于水中(如图乙),杆
将会__________(选填“左端下降”“右端
下降”或“仍然平衡”),试通过推导说明。
解:∵杠杆平衡时,有:F1×L1=F2×L2
∴m1g×L1=m2g×L2
变形得到L1∶L2=m2∶m1
仍然平衡
提高训练
解:以浸没于水的物体为研究对象进行受力分析:
F拉+F浮=m物g
F拉=m物g-F浮=m物g-ρ水gV物=(1- )m物g
所以:F拉1×L1=(1- )m1gL1
F拉2×L2=(1- )m2gL2
∵m1gL1=m2gL2
∴F拉1×L1=F拉2×L2
因此杠杆仍然平衡
提高训练
5.在“大力士”比赛中,需要把一质量m=400 kg,边长l=1 m,质量分布均匀的立方体,利用翻滚的方法沿直线移动一段距离,如图所示,g取10 N/kg.求:翻滚立方体时,使立方体一边刚刚离开地面,所用最小力F的大小.
解:根据杠杆平衡条件得F×l1=G×l2,代入数据得F= ≈1.414×103 N
提高训练
6. 如图所示,一根质量分布均匀的木棒,质量为m,长度为L,竖直悬挂在转轴O处。在木棒最下端用一方向始终水平向右的拉力F缓慢将木棒拉动到与竖直方向夹角为θ的位置(转轴处摩擦不计)。问:
(1)画出θ=60°时拉力F的力臂l,并计算力臂的大小;
(2)木棒的重力作用点在其长度的二分之一处,随拉
开角度θ的增加,拉力F将如何变化?并推导拉力F
与角度θ的关系式。
解:l=L×cos60°=0.5L
(2)F随拉开角度θ的增加将变大
根据杠杆平衡条件可得
mg×0.5×L×sinθ=F×cosθ×L
F=0.5mg tanθ
浙教版 科学(初中)
九上期末复习课(六)
杠杆及其应用
杠杆:在力的作用下,能绕固定点
转动的硬棒叫杠杆。
1.杠杆的定义
支点o
动力臂L1
L2阻力臂
阻力F2
动力F1
杠杆类型 杠杆特点 杠杆优点 杠杆缺点 应用
省力杠杆
费力杠杆
等臂杠杆
L1>L2
F1
省力
费距离
省距离
费力
既不省力也不省距离
L1
(动力>阻力)
L1=L2
F1=F2
(动力=阻力)
2.杠杆的分类
人体中的杠杆举例
(1)走路时的脚——省力杠杆
脚掌前部是支点,人体的重力是________力,腿部肌肉产生的拉力是________力,这种杠杆可以克服较大的体重。
阻
阻
(2)做俯卧撑——省力杠杆
脚掌前部是支点,人体的重力是阻力,手臂肌肉产生的支持力是动力。
(3)仰卧起坐
仰卧起坐(腿部不动,用腹肌使整个上身起来):支点是臀部与支持面的接触点,阻力是上半身的重力,动力是腹肌肌肉产生的拉力,动力臂小于阻力臂,是费力杠杆。
3、杠杆的平衡条件
杠杆在动力和阻力的作用下,保持静止状态或匀速转动状态,我们就说杠杆处于平衡。
L1
L2
FI
F2
研究杠杆的平衡
(1)把杠杆的中央支在支架上,调节杠杆两端的螺母,使杠杆在水平位置处于平衡状态。
(2)在杠杆的两端分别挂上不同数量的钩码,并左右移动钩码悬挂的位置,直到杠杆再次在水平
位置处于平衡状态。这时杠杆两端受到的作用力分别等于各自钩码的重力。将支点左边钩码
对杠杆作用力记作动力F1,右边钩码对杠杆作用力记作阻力 F2。将动力和阻力填入表内。
(3) 读出动力臂 l1、阻力臂 l2,并填入表内。
(4) 改变力和力臂的数值,重复上述实验,共做 4 次。把有关数据填入表内。
序号 动力F1(牛) 动力臂l1(厘米) F1×l1 阻力F2(牛) 阻力臂l2(厘米) F2×l2
1
2
3
4
3
10
2
15
4
20
2
10
6
10
4
15
2
20
10
1
20
30
40
60
20
30
40
60
记录表
杠杆的平衡条件是:动力乘以动力臂
等于阻力乘以阻力臂即:F1×L1=F2×L2
4.最小力问题
图中的杠杆处于水平位置并静止,B端绳子的拉力F沿哪个方向时用力最小?
L阻
L1
F1
F2
F4
F3
C
D
O
沿F2方向用力时动力臂最大,所以F2最小
L2
L3
L4
提示:比较F沿不同方向时力臂的大小。
F阻一般是不能改变的。
由杠杆平衡条件得:F动×L动=F阻×L阻
减小动力的方法:
1、减小阻力臂L阻
2、增大动力臂L动
通过对省力杠杆和费力杠杆的进一步分析,可以发现:
使用省力杠杆虽然省力,但是动力移动的距离比阻力移动的距离大。
而使用费力杠杆虽然费力,但是动力移动的距离比阻力移动的距离小。
基础过关
1、如图所示的杠杆中,O是支点,在B端挂一个重物,为使杠杆水平平衡,要在A端加一个力,下列说法中正确的是( )
A.在水平方向用力F1最小
B.在竖直方向用力F2最小
C.在跟OA连线垂直的方向F3最小
D.在各个方向上用力一样大
C
基础过关
2. 小金将长为0.6米、质量可忽略不计的木棒搁在肩上,棒的后端A挂一个40牛的物体,肩上支点O离后端A为0.2米,他用手压住前端B使木棒保持水平平衡,如图所示,小金的质量为50千克,则此时手压木棒的力大小为______牛,肩对木棒的支持力大小为________牛,人对地面的压力大小为________牛(g=10牛/千克)。
20
60
540
基础过关
3.如图所示,将长为1.2米的轻质木棒平放在水平方形台面上,左右两端点分别为A、B,它们距台面边缘处的距离均为0.3米。在A端挂一个重为30牛的物体,在B端挂一个重为G的物体。
(1)若G=30牛,台面受到木棒的压力为________牛。
(2)若要使木棒右端下沉,B端挂的物体至少要大于________牛。
(3)若B端挂物体后,木棒仍在水平台面上静止,则G的取值范围为________牛。
60
90
10~90
基础过关
4.在“探究杠杆的平衡条件”实验中:
(1)实验前调节杠杆在水平位置平衡,目的是____________________________.
(2)通过多次实验得出表格数据:
方便直接在杠杆上读出力臂
次数 F1/N l1/cm F2/N l2/cm
1 2 2 1 4
2 2 4 1 8
3 2 6 1 12
4 1 16 2 8
5 2 10 1 20
6 3 8 2 12
基础过关
分析1、2、3次实验数据,可以发现实验中存在的问题是:没有改变________的大小.
(3)分析4、5、6次实验数据,得出杠杆的平衡条件是____________(用字母表示)
(4)如图甲所示是某次实验中的情形,把图中杠杆
两侧的钩码各取下一个,为使杠杆再次在水平位
置平衡,应将左侧钩码向________移动一个格同
时右侧钩码向________移动一个格.(选填“左”
或“右”)
例题图甲
力
F1l1=F2l2
右
左
基础过关
(5)实验前在调节杠杆平衡时,若杠杆静止时左端高右端低,此时杠杆处于________(选填“平衡”或“非平衡”)状态,此时应将杠杆两端的平衡螺母向________(选填“左”或“右”)调节.
(6)实验中改变钩码质量和力臂进行多次实验的目的是_____________________.
平衡
左
使得出的结论具有普遍性
基础过关
拓展设问题图乙
(7)将杠杆一侧的钩码换成弹簧测力计,先后进行如图乙所示的两次实验,第一次弹簧测力计竖直向下拉,示数为F1;第二次弹
簧测力计斜着拉,示数为F2.若两次杠杆保持水平
平衡,则当弹簧测力计由第一种位置转至第二种
位置的过程中,弹簧测力计的示数F1________(选
填“>”“<”或“=”)F2.
(8)进行完实验后,探讨以下三个因素对实验
的影响:①支架自身的重力足够大;②单个钩码的重力不完全相等;③杠杆与转轴之间的摩擦偏大.其中不会带来实验误差的是________(填序号).
<
①
基础过关
(9)小明同学所在的实验小组在完成规定实验后,他们想进一步研究,如果杠杆受到F2、F3两个阻力,结果会怎样?通过实验,
他们得到了如图丙所示的结果,根据这个结果,
可以初步得出,在这种情况下杠杆的平衡条件
为:F1L1=____________(用F2、F3、L2、L3表示).
相比图乙所示的方法,利用这种方法进行探究
的不足之处是____________________________
________________________________________.
图丙
F2L2+F3L3
杠杆右端力臂数量太多,不便于得出实验结论
提高训练
1、衣服夹是一种常用物品,如图所示,给出了用手捏开和夹住物品时的两种情况。下列说法中,正确的是( )
A.当用手将其捏开时,它是费力杠杆
B.当用其夹住物品时,它是费力杠杆
C.无论用手将其捏开还是夹住物品时,它都是费力杠杆
D.无论用手将其捏开还是夹住物品时,它都是省力杠杆
B
提高训练
2、如图所示,足够长的杠杆上放着质量不相等(m1>m2)的两个球,杠杆在水平位置平衡,若两球以相同速度同时向远离支点的方向运动相等的时间,则杠杆 ( )
A.仍平衡
B.大球那端下沉
C.小球那端下沉
D.无法确定
B
提高训练
3、如图所示,某同学发现了一个金属块。他想知道它的重力和密度。他手中只有一只量程较小的弹簧秤,当他用此弹簧秤测量此金属块的重力时,发现已超过弹簧秤的最大量程,于是他设计了如图所示的装置。OA∶AB=1∶3,用弹簧秤在B点施加一个竖直向上的力,当OB杠杆水平静止时,弹簧秤读数为1.8 N,当向容器中加水,金属块浸没于水中后,弹簧秤读数为1.2 N,则金属块受到的重力是__________N;密度是_____________kg/m3。
7.2
3×103
提高训练
4.如图甲,有一轻质杆,左右各挂由同种金属制成、质量分别为m1和m2(m1>m2)的实心物块后恰好水平平衡。
(1)求左右悬挂点到支点O的距离L1与L2之比。
(2)将两物分别浸没于水中(如图乙),杆
将会__________(选填“左端下降”“右端
下降”或“仍然平衡”),试通过推导说明。
解:∵杠杆平衡时,有:F1×L1=F2×L2
∴m1g×L1=m2g×L2
变形得到L1∶L2=m2∶m1
仍然平衡
提高训练
解:以浸没于水的物体为研究对象进行受力分析:
F拉+F浮=m物g
F拉=m物g-F浮=m物g-ρ水gV物=(1- )m物g
所以:F拉1×L1=(1- )m1gL1
F拉2×L2=(1- )m2gL2
∵m1gL1=m2gL2
∴F拉1×L1=F拉2×L2
因此杠杆仍然平衡
提高训练
5.在“大力士”比赛中,需要把一质量m=400 kg,边长l=1 m,质量分布均匀的立方体,利用翻滚的方法沿直线移动一段距离,如图所示,g取10 N/kg.求:翻滚立方体时,使立方体一边刚刚离开地面,所用最小力F的大小.
解:根据杠杆平衡条件得F×l1=G×l2,代入数据得F= ≈1.414×103 N
提高训练
6. 如图所示,一根质量分布均匀的木棒,质量为m,长度为L,竖直悬挂在转轴O处。在木棒最下端用一方向始终水平向右的拉力F缓慢将木棒拉动到与竖直方向夹角为θ的位置(转轴处摩擦不计)。问:
(1)画出θ=60°时拉力F的力臂l,并计算力臂的大小;
(2)木棒的重力作用点在其长度的二分之一处,随拉
开角度θ的增加,拉力F将如何变化?并推导拉力F
与角度θ的关系式。
解:l=L×cos60°=0.5L
(2)F随拉开角度θ的增加将变大
根据杠杆平衡条件可得
mg×0.5×L×sinθ=F×cosθ×L
F=0.5mg tanθ
同课章节目录
