5.1.1相交线同步习题及答案
文档属性
| 名称 | 5.1.1相交线同步习题及答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 62.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-01-18 00:00:00 | ||
图片预览


文档简介
5.1.1 相交线
一、选择题:
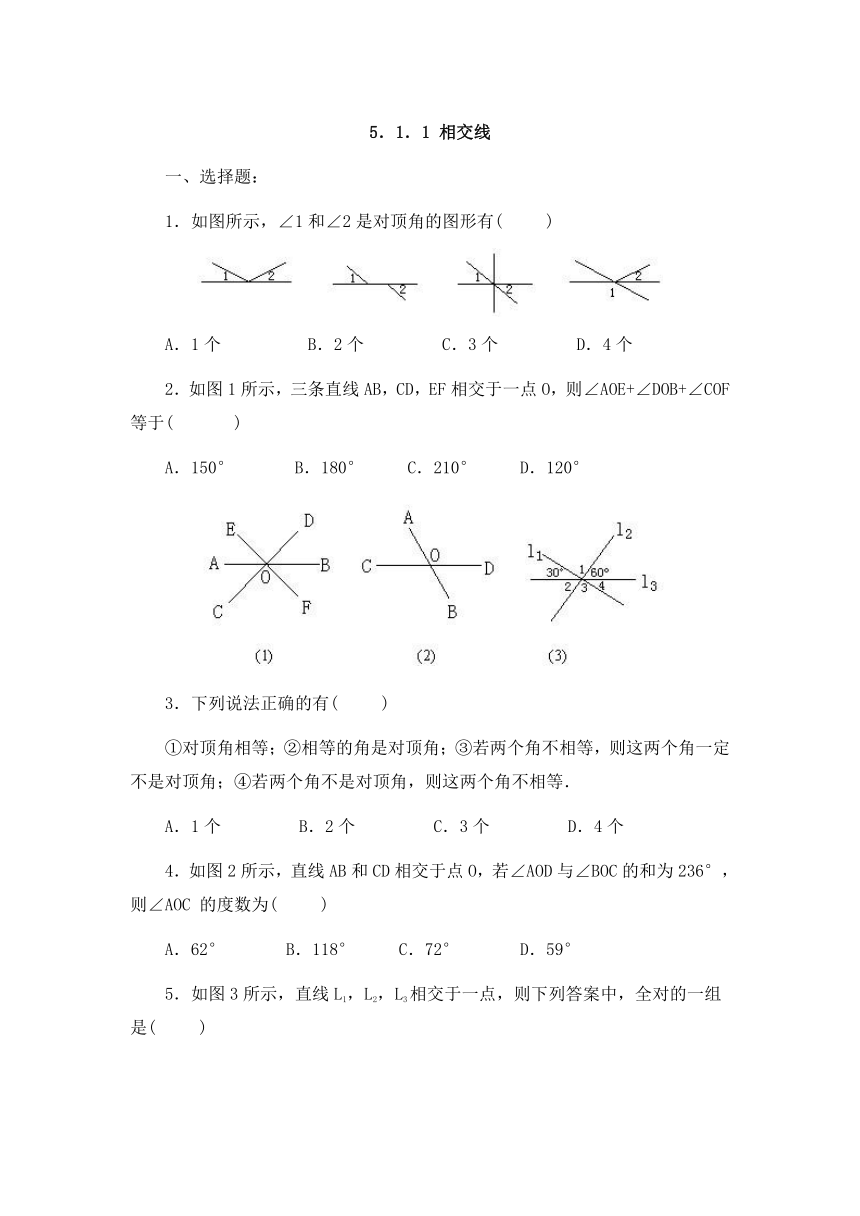
1.如图所示,∠1和∠2是对顶角的图形有( )毛
A.1个 B.2个 C.3个 D.4个
2.如图1所示,三条直线AB,CD,EF相交于一点O,则∠AOE+∠DOB+∠COF等于( )
A.150° B.180° C.210° D.120°
3.下列说法正确的有( )
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个 B.2个 C.3个 D.4个
4.如图2所示,直线AB和CD相交于点O,若∠AOD与∠BOC的和为236°,则∠AOC的度数为( )
A.62° B.118° C.72° D.59°
5.如图3所示,直线L1,L2,L3相交于一点,则下列答案中,全对的一组是( )
A.∠1=90°,∠2=30°,∠3=∠4=60°; B.∠1=∠3=90°,∠2=∠4=30
C.∠1=∠3=90°,∠2=∠4=60°;
D.∠1=∠3=90°,∠2=60°,∠4=30°
二、填空题:
1.如图4所示,AB与CD相交所成的四个角中,∠1的邻补角是______,∠1的对顶角___.
2.如图4所示,若∠1=25°,则∠2=_______,∠3=______,∠4=_______.
3.如图5所示,直线AB,CD,EF相交于点O,则∠AOD的对顶角是_____,∠AOC的邻补角是_______;若∠AOC=50°,则∠BOD=______,∠COB=_______.
4.如图6所示,已知直线AB,CD相交于O,OA平分∠EOC,∠EOC=70°,则∠BOD=______.
5.对顶角的性质是______________________.
6.如图7所示,直线AB,CD相交于点O,若∠1 ∠2=70 ,则∠BOD=_____,∠2=____.
7.如图8所示,直线AB,CD相交于点O,OE平分∠AOC,若∠AOD ∠DOB=50°,则∠EOB=______________.
8.如图9所示,直线AB,CD相交于点O,已知∠AOC=70°,OE把∠BOD分成两部分,且∠BOE:∠EOD=2:3,则∠EOD=________.
三、训练平台:
1.如图所示,AB,CD,EF交于点O,∠1=20°,∠BOC=80°,求∠2的度数.
2.如图所示,L1,L2,L3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.
四、提高训练:
1.如图所示,AB,CD相交于点O,OE平分∠AOD,∠AOC=120°,求∠BOD,∠AOE的度数.
2.如图所示,直线AB与CD相交于点O,∠AOC:∠AOD=2:3,求∠BOD的度数.
3.如图所示,直线a,b,c两两相交,∠1=2∠3,∠2=65°,求∠4的度数.
五、探索发现:
1.若4条不同的直线相交于一点,则图中共有几对对顶角?若n条不同的直线相交于一点呢?
2.在一个平面内任意画出6条直线,最多可以把平面分成几个部分?n条直线呢?
六、能力提高:
已知点O是直线AB上一点,OC,OD是两条射线,且∠AOC=∠BOD,则∠AOC与∠BOD是对顶角吗?为什么?
七、中考题与竞赛题:
(2001.南通)如图16所示,直线AB,CD相交于O,若∠1=40°,则∠2的度数为____
参考答案
一、1.A 2.B 3.B 4.A 5.D
二、1.∠2和∠4 ∠3 2.155° 25° 155° 4.35° 5.对顶角相等
6 .125° 55° 7.147.5° 8.42°
三、1.∠2=60° 2.∠4=36°
四、1.∠BOD=120°,∠AOE=30° 2.∠BOD=72° 3.∠4=32.5°
五、
1.4条不同的直线相交于一点,图中共有12对对顶角(平角除外),n条不同的直线相交于一点,图中共有(n2 n)对对顶角(平角除外).
2.6条直线最多可以把平面分成22个部分,n条直线最多可以把平面分成个部分.
六、∠AOC与∠BOD不一定是对顶角.如图1所示,当射线OC,OD位于直线AB的一侧时,不是对顶角;如图2所示,当射线OC,OD位于直线AB的两侧时,是对顶角.
七、140°.毛
一、选择题:
1.如图所示,∠1和∠2是对顶角的图形有( )毛
A.1个 B.2个 C.3个 D.4个
2.如图1所示,三条直线AB,CD,EF相交于一点O,则∠AOE+∠DOB+∠COF等于( )
A.150° B.180° C.210° D.120°
3.下列说法正确的有( )
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个 B.2个 C.3个 D.4个
4.如图2所示,直线AB和CD相交于点O,若∠AOD与∠BOC的和为236°,则∠AOC的度数为( )
A.62° B.118° C.72° D.59°
5.如图3所示,直线L1,L2,L3相交于一点,则下列答案中,全对的一组是( )
A.∠1=90°,∠2=30°,∠3=∠4=60°; B.∠1=∠3=90°,∠2=∠4=30
C.∠1=∠3=90°,∠2=∠4=60°;
D.∠1=∠3=90°,∠2=60°,∠4=30°
二、填空题:
1.如图4所示,AB与CD相交所成的四个角中,∠1的邻补角是______,∠1的对顶角___.
2.如图4所示,若∠1=25°,则∠2=_______,∠3=______,∠4=_______.
3.如图5所示,直线AB,CD,EF相交于点O,则∠AOD的对顶角是_____,∠AOC的邻补角是_______;若∠AOC=50°,则∠BOD=______,∠COB=_______.
4.如图6所示,已知直线AB,CD相交于O,OA平分∠EOC,∠EOC=70°,则∠BOD=______.
5.对顶角的性质是______________________.
6.如图7所示,直线AB,CD相交于点O,若∠1 ∠2=70 ,则∠BOD=_____,∠2=____.
7.如图8所示,直线AB,CD相交于点O,OE平分∠AOC,若∠AOD ∠DOB=50°,则∠EOB=______________.
8.如图9所示,直线AB,CD相交于点O,已知∠AOC=70°,OE把∠BOD分成两部分,且∠BOE:∠EOD=2:3,则∠EOD=________.
三、训练平台:
1.如图所示,AB,CD,EF交于点O,∠1=20°,∠BOC=80°,求∠2的度数.
2.如图所示,L1,L2,L3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.
四、提高训练:
1.如图所示,AB,CD相交于点O,OE平分∠AOD,∠AOC=120°,求∠BOD,∠AOE的度数.
2.如图所示,直线AB与CD相交于点O,∠AOC:∠AOD=2:3,求∠BOD的度数.
3.如图所示,直线a,b,c两两相交,∠1=2∠3,∠2=65°,求∠4的度数.
五、探索发现:
1.若4条不同的直线相交于一点,则图中共有几对对顶角?若n条不同的直线相交于一点呢?
2.在一个平面内任意画出6条直线,最多可以把平面分成几个部分?n条直线呢?
六、能力提高:
已知点O是直线AB上一点,OC,OD是两条射线,且∠AOC=∠BOD,则∠AOC与∠BOD是对顶角吗?为什么?
七、中考题与竞赛题:
(2001.南通)如图16所示,直线AB,CD相交于O,若∠1=40°,则∠2的度数为____
参考答案
一、1.A 2.B 3.B 4.A 5.D
二、1.∠2和∠4 ∠3 2.155° 25° 155° 4.35° 5.对顶角相等
6 .125° 55° 7.147.5° 8.42°
三、1.∠2=60° 2.∠4=36°
四、1.∠BOD=120°,∠AOE=30° 2.∠BOD=72° 3.∠4=32.5°
五、
1.4条不同的直线相交于一点,图中共有12对对顶角(平角除外),n条不同的直线相交于一点,图中共有(n2 n)对对顶角(平角除外).
2.6条直线最多可以把平面分成22个部分,n条直线最多可以把平面分成个部分.
六、∠AOC与∠BOD不一定是对顶角.如图1所示,当射线OC,OD位于直线AB的一侧时,不是对顶角;如图2所示,当射线OC,OD位于直线AB的两侧时,是对顶角.
七、140°.毛
