平移同步练习
图片预览

文档简介
5.4 平移
◆回顾归纳
1.平移的要素:(1)平移的_________;(2)平移的_________.
2.(1)平移:将一个图形沿某个方向_________叫平移.
(2)平移的性质:对应点的连结线段_________且_________.
3.平移作图方法:
(1)找出已知图形上的关键点;
(2)过这些点沿指定_______平移,使平移_______等于已知距离;
(3)依次作出各个_______点,连结所平移后的点得平移图形.
◆课堂测控
知识点 平移
1.(1)将线段AB向北偏东方向平移5cm,则点A平移方向_______,平移距离为______.(2)经过平移后的图形与______形状和大小都不改变.
2.下列物体运动中平移的是_________(填序号).
(1)打乒乓球的运动;(2)手表上指针的运动;
(3)汽车在笔直公路上运动;(4)车轮的滚动.
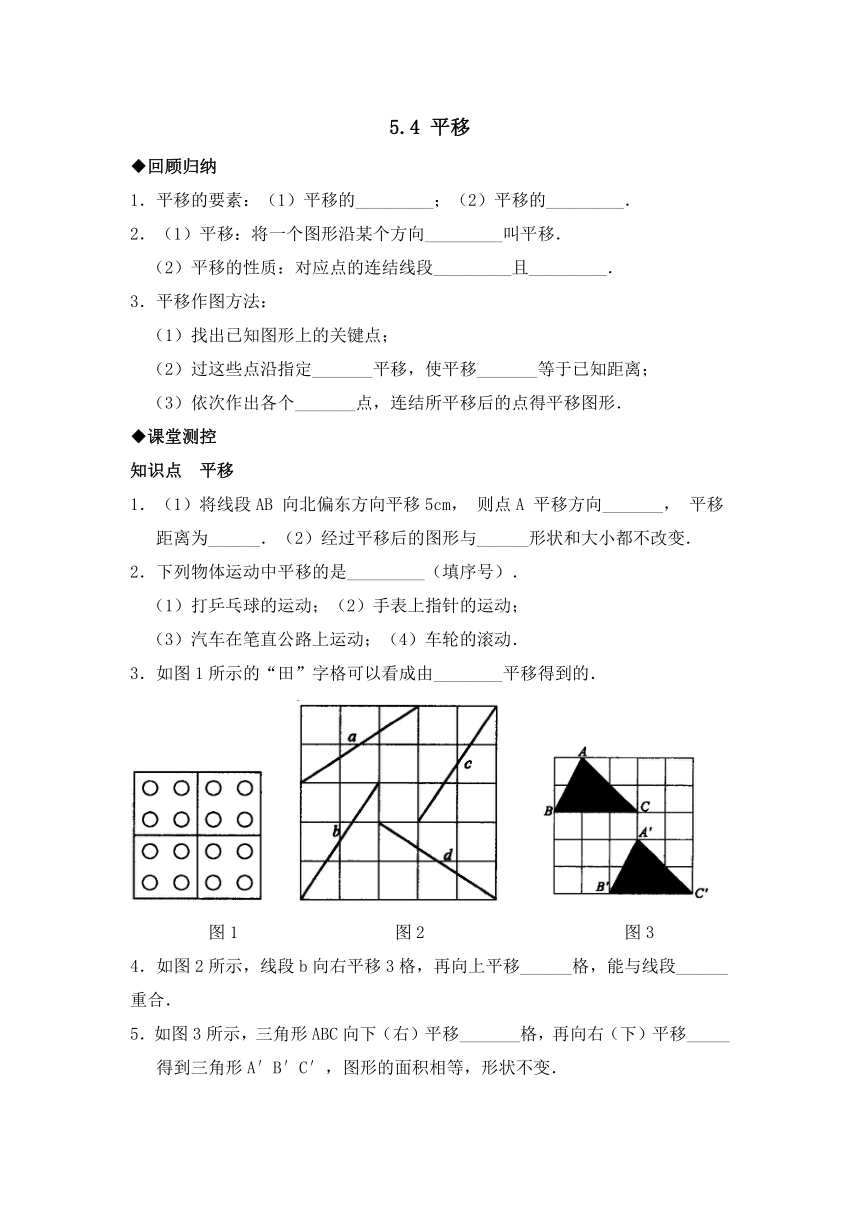
3.如图1所示的“田”字格可以看成由________平移得到的.
图1 图2 图3
4.如图2所示,线段b向右平移3格,再向上平移______格,能与线段______重合.
5.如图3所示,三角形ABC向下(右)平移_______格,再向右(下)平移_____得到三角形A′B′C′,图形的面积相等,形状不变.
6.下列各组图形可以通过平移得到另一个图形的是( )
A B C D
7.(经典题)如图4所示,长方形ABCD中,对角线AC,BD交于点O.DE∥AC,CE∥BC.那么三角形EDC可以看成什么三角形平移得到的,指出平移方向,并求出平移距离?
图4
◆课后测控
1.将正方形ABCD向北偏东30°方向平移4cm,则对角线交点O向________平移______cm.
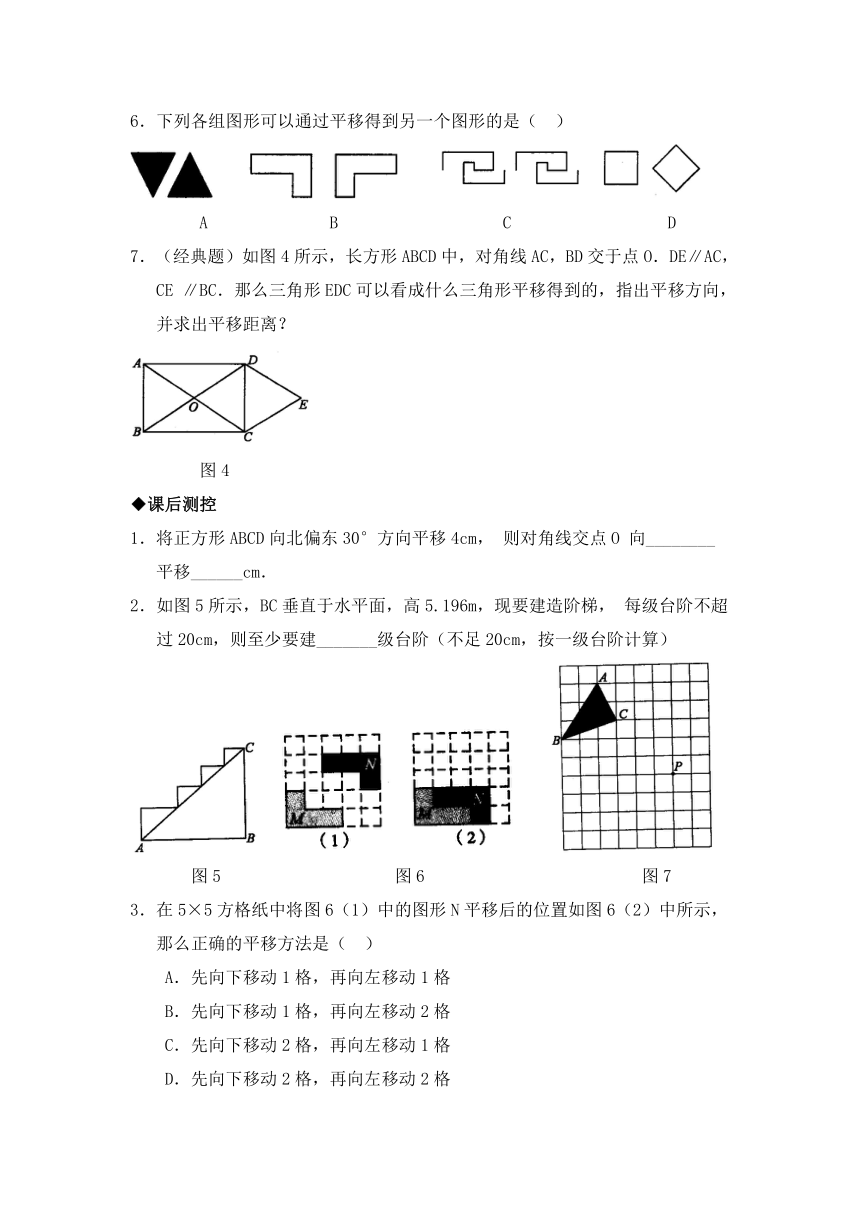
2.如图5所示,BC垂直于水平面,高5.196m,现要建造阶梯,每级台阶不超过20cm,则至少要建_______级台阶(不足20cm,按一级台阶计算)
图5 图6 图7
3.在5×5方格纸中将图6(1)中的图形N平移后的位置如图6(2)中所示,那么正确的平移方法是( )
A.先向下移动1格,再向左移动1格
B.先向下移动1格,再向左移动2格
C.先向下移动2格,再向左移动1格
D.先向下移动2格,再向左移动2格
4.(互动探究题)如图7所示,在网格中,有三角形ABC,将A点平移到P点,画出三角形ABC平移后的图形.
[解答]
(1)将A点向_______(或向______)平移______格(或_____格).
(2)再向_____(或向_____)平移______格(或_______格),得点P.
(3)同理B,C与A点平移次数方向距离一样,易得B′,C′.
(4)连结PB′,PC′,B′C′得到三角形ABC平移后的三角形PB′C′.
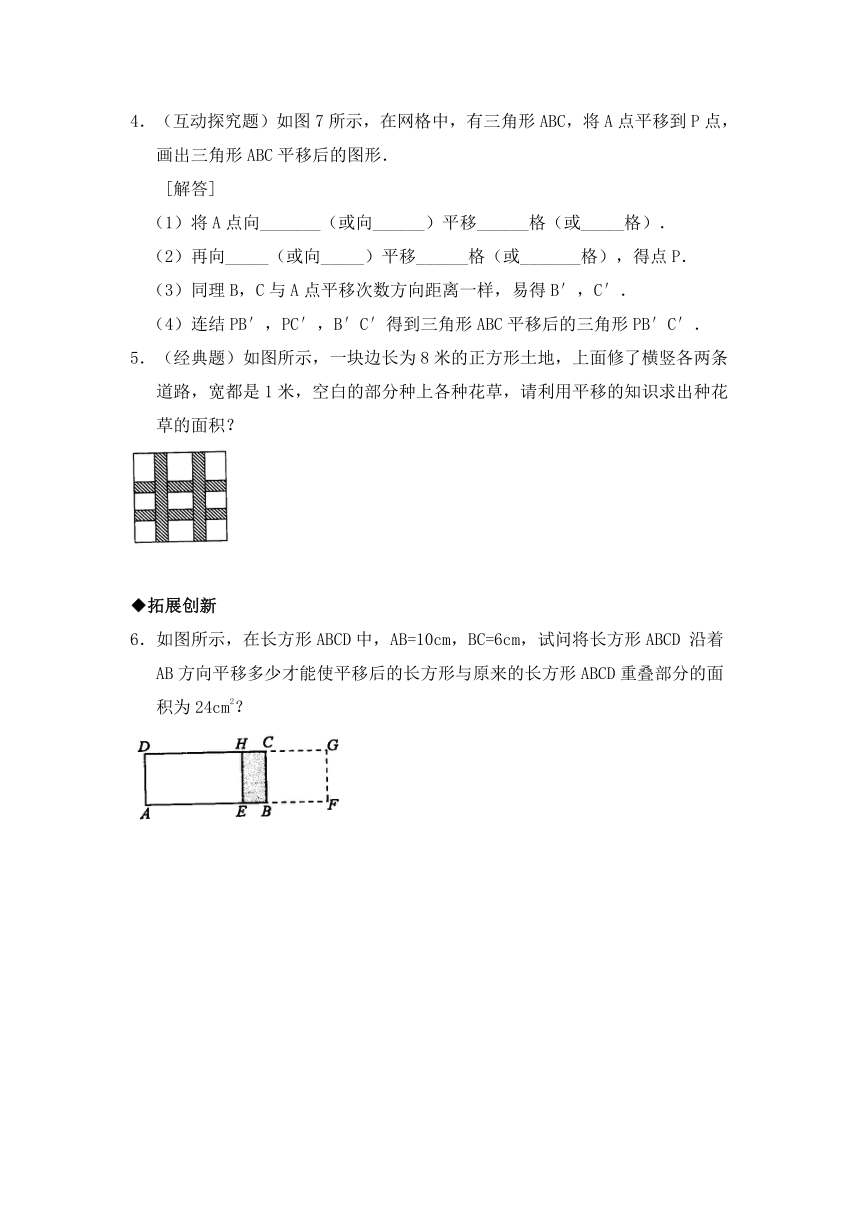
5.(经典题)如图所示,一块边长为8米的正方形土地,上面修了横竖各两条道路,宽都是1米,空白的部分种上各种花草,请利用平移的知识求出种花草的面积?
◆拓展创新
6.如图所示,在长方形ABCD中,AB=10cm,BC=6cm,试问将长方形ABCD沿着AB方向平移多少才能使平移后的长方形与原来的长方形ABCD重叠部分的面积为24cm2?
参考答案
回顾归纳
1.(1)方向 (2)距离
2.(1)移动 (2)平行或在同一条直线上,相等
3.(2)方向;距离(3)对应
课堂测控
1.(1)北偏东;5cm (2)原图形 2.(3)
3.小正方形包括中间四个小圆圈为基本图形
4.2,c 5.3(或2),2(或3)
6.C(点拨:A,B,D都不能通过平移得到)
7.由三角形AOB,向右平移,平移距离为AD长.
解题技巧:由平移图形的特征:大小,形状不变,猜想是△AOB.
课后测控
1.北偏东30°;4 2.26(点拨:=26)
3.C(点拨:或向左平移1格,再向下平移2格)
4.(1)右;(下);4;(5) (2)下;(右);5;(4) (3),(4)图略
5.将两条道路平移得到如图所示,则空白面积为(8-2)(8-2)=36(m2)
思路点拨:运用平移思想方法是求这类面积问题最佳途径.
6.设平行线段AE=x,A到E,E到F,则BE=AB-AE=10-x,因为BC=6,所以6(10-x)=24,解得x=6,向右平移6cm.
解题规律:扣住HEBC面积为24cm2,运用方程思想求解.
5.4 平移同步练习2
一、选择题:(每小题3分,共15分)毛
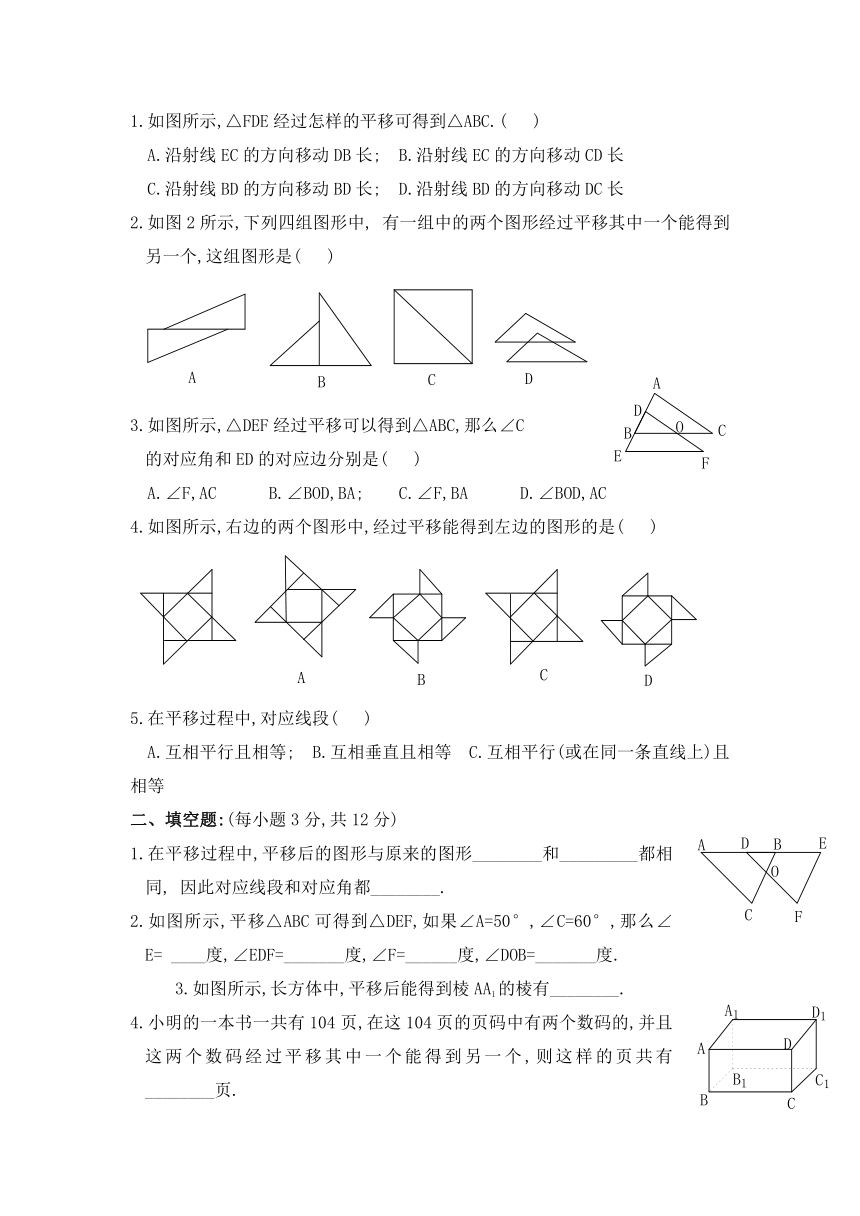
1.如图所示,△FDE经过怎样的平移可得到△ABC.( )
A.沿射线EC的方向移动DB长; B.沿射线EC的方向移动CD长
C.沿射线BD的方向移动BD长; D.沿射线BD的方向移动DC长
2.如图2所示,下列四组图形中,有一组中的两个图形经过平移其中一个能得到 另一个,这组图形是( )
3.如图所示,△DEF经过平移可以得到△ABC,那么∠C
的对应角和ED的对应边分 别是( )
A.∠F,AC B.∠BOD,BA; C.∠F,BA D.∠BOD,AC
4.如图所示,右边的两个图形中,经过平移能得到左边的图形的是( )
5.在平移过程中,对应线段( )
A.互相平行且相等; B.互相垂直且相等 C.互相平行(或在同一条直线上)且相等
二、填空题:(每小题3分,共12分)
1.在平移过程中,平移后的图形与原来的图形________和_________都相同,因 此对应线段和对应角都________.
2.如图所示,平移△ABC可得到△DEF,如果∠A=50°,∠C=60°,那么∠E=____ 度,∠EDF=_______度,∠F=______度,∠DOB=_______度.
3.如图所示,长方体中,平移后能得到棱AA1的棱有________.
4.小明的一本书一共有104页,在这104页的页码中有两个数码的,并且这两个数 码经过平移其中一个能得到另一个,则这样的页共有________页.
三、训练平台:(每小题5分,共15分)
1.如图所示,请将图中的“蘑菇”向左平移6个格,再向下平移2个格.
(第1题) (第2题) (第3题)
2.如图所示,将△ABC平移,可以得到△DEF,点B的对应点为点E,请画出点A的对 应点D、点C的对应点F的位置.
3.如图所示,画出平行四边形ABCD向上平移1厘米后的图形.
四、提高训练:(每小题6分,共12分)
1.如图所示的是某商品包装盒上图案的一部分,请分析这个图案的基本图形 和形成过程.
2.如图所示,四边形ABCD中,AD∥BC,AB=DC=AD,将DC向左平移AD长,平移后你 得到的两个图形是什么样的
五、探索发现:(共8分)
公路上同向而行的两辆汽车,从后车车头与前车车尾“相遇”到原后车车尾离 开原车车头这段时间为超车时间,如果原前、后两车车长分别为a,b,那么在超车时 间内两车行驶的路程与两车车长有何关系
六、能力提高:(每小题9分,共18分)
1.如图所示,四边形ABCD中,AD∥BC,AB=DC,∠B=80°,求∠A,∠D,∠C的度数.
2.如图所示,大圆O内有一小圆O1,小圆O1从现在的位置沿O1O的方向平移4个 单位后,得到小圆O2,已知小圆半径为1.
(1)求大圆的面积;(2)求小圆在平移过程中扫过的面积.
七、中考题与竞赛题:(每小题10分,共20分)
1.(2013.福建)如图14所示,点A,B,C,D在同一条直线上,AB=CD,∠D=∠ECA,EC= FD.试说明AE=BF.
2.如图15所示的是用火柴杆摆的一只向左飞行的小鸟,你能只平移3根火柴杆就 使它向右飞吗
参考答案:
一、1.A 2.D 3.C 4.C 5.C
二、1.形状 大小 相等 2.70 50 60 60 3.BB1,CC1,DD1 4.9
三、1.提示:先画出主要点的对应点,然后再连线.
2.提示:过点E作BA,BC的平行线,再截取DE=AB,FE=CB.
3.略
四、1.提示:基本图形是 ,由这个图形平移得到.
2.如图7所示,△ABC′是等腰三角形,四边形AC′CD是菱形.
五、解:如图8所示,两车行驶的路程即平移的距离,从图中很容易看出:在超车 时间内两车的路程差等于a+b.
六、1.解:将CD沿DA方向平移DA长(如图9所示),显然BA=CD=EA,所以△ABE是等 腰三角形,∠AEB=∠B=80°,又AE∥CD,∴∠C=∠AEB=80°,又AD∥BC,∴∠D+∠C=18 0°,∠D=100°,同理可得∠BAD=100°.
2.解:(1)根据平移知识可知MN=4(如图10所示),又∵小圆半径为1,∴大圆直 径PN=大圆面积为 =;
(2)小圆平移时扫过的面积为长方形ABCD的面积+小圆面积 =2×4+.
七、1.提示:根据已知条件可知,将△AEC平移后可得到△BFD,根据对应线段相 等,可得AE=BF.
2.解:如图11所示.毛
◆回顾归纳
1.平移的要素:(1)平移的_________;(2)平移的_________.
2.(1)平移:将一个图形沿某个方向_________叫平移.
(2)平移的性质:对应点的连结线段_________且_________.
3.平移作图方法:
(1)找出已知图形上的关键点;
(2)过这些点沿指定_______平移,使平移_______等于已知距离;
(3)依次作出各个_______点,连结所平移后的点得平移图形.
◆课堂测控
知识点 平移
1.(1)将线段AB向北偏东方向平移5cm,则点A平移方向_______,平移距离为______.(2)经过平移后的图形与______形状和大小都不改变.
2.下列物体运动中平移的是_________(填序号).
(1)打乒乓球的运动;(2)手表上指针的运动;
(3)汽车在笔直公路上运动;(4)车轮的滚动.
3.如图1所示的“田”字格可以看成由________平移得到的.
图1 图2 图3
4.如图2所示,线段b向右平移3格,再向上平移______格,能与线段______重合.
5.如图3所示,三角形ABC向下(右)平移_______格,再向右(下)平移_____得到三角形A′B′C′,图形的面积相等,形状不变.
6.下列各组图形可以通过平移得到另一个图形的是( )
A B C D
7.(经典题)如图4所示,长方形ABCD中,对角线AC,BD交于点O.DE∥AC,CE∥BC.那么三角形EDC可以看成什么三角形平移得到的,指出平移方向,并求出平移距离?
图4
◆课后测控
1.将正方形ABCD向北偏东30°方向平移4cm,则对角线交点O向________平移______cm.
2.如图5所示,BC垂直于水平面,高5.196m,现要建造阶梯,每级台阶不超过20cm,则至少要建_______级台阶(不足20cm,按一级台阶计算)
图5 图6 图7
3.在5×5方格纸中将图6(1)中的图形N平移后的位置如图6(2)中所示,那么正确的平移方法是( )
A.先向下移动1格,再向左移动1格
B.先向下移动1格,再向左移动2格
C.先向下移动2格,再向左移动1格
D.先向下移动2格,再向左移动2格
4.(互动探究题)如图7所示,在网格中,有三角形ABC,将A点平移到P点,画出三角形ABC平移后的图形.
[解答]
(1)将A点向_______(或向______)平移______格(或_____格).
(2)再向_____(或向_____)平移______格(或_______格),得点P.
(3)同理B,C与A点平移次数方向距离一样,易得B′,C′.
(4)连结PB′,PC′,B′C′得到三角形ABC平移后的三角形PB′C′.
5.(经典题)如图所示,一块边长为8米的正方形土地,上面修了横竖各两条道路,宽都是1米,空白的部分种上各种花草,请利用平移的知识求出种花草的面积?
◆拓展创新
6.如图所示,在长方形ABCD中,AB=10cm,BC=6cm,试问将长方形ABCD沿着AB方向平移多少才能使平移后的长方形与原来的长方形ABCD重叠部分的面积为24cm2?
参考答案
回顾归纳
1.(1)方向 (2)距离
2.(1)移动 (2)平行或在同一条直线上,相等
3.(2)方向;距离(3)对应
课堂测控
1.(1)北偏东;5cm (2)原图形 2.(3)
3.小正方形包括中间四个小圆圈为基本图形
4.2,c 5.3(或2),2(或3)
6.C(点拨:A,B,D都不能通过平移得到)
7.由三角形AOB,向右平移,平移距离为AD长.
解题技巧:由平移图形的特征:大小,形状不变,猜想是△AOB.
课后测控
1.北偏东30°;4 2.26(点拨:=26)
3.C(点拨:或向左平移1格,再向下平移2格)
4.(1)右;(下);4;(5) (2)下;(右);5;(4) (3),(4)图略
5.将两条道路平移得到如图所示,则空白面积为(8-2)(8-2)=36(m2)
思路点拨:运用平移思想方法是求这类面积问题最佳途径.
6.设平行线段AE=x,A到E,E到F,则BE=AB-AE=10-x,因为BC=6,所以6(10-x)=24,解得x=6,向右平移6cm.
解题规律:扣住HEBC面积为24cm2,运用方程思想求解.
5.4 平移同步练习2
一、选择题:(每小题3分,共15分)毛
1.如图所示,△FDE经过怎样的平移可得到△ABC.( )
A.沿射线EC的方向移动DB长; B.沿射线EC的方向移动CD长
C.沿射线BD的方向移动BD长; D.沿射线BD的方向移动DC长
2.如图2所示,下列四组图形中,有一组中的两个图形经过平移其中一个能得到 另一个,这组图形是( )
3.如图所示,△DEF经过平移可以得到△ABC,那么∠C
的对应角和ED的对应边分 别是( )
A.∠F,AC B.∠BOD,BA; C.∠F,BA D.∠BOD,AC
4.如图所示,右边的两个图形中,经过平移能得到左边的图形的是( )
5.在平移过程中,对应线段( )
A.互相平行且相等; B.互相垂直且相等 C.互相平行(或在同一条直线上)且相等
二、填空题:(每小题3分,共12分)
1.在平移过程中,平移后的图形与原来的图形________和_________都相同,因 此对应线段和对应角都________.
2.如图所示,平移△ABC可得到△DEF,如果∠A=50°,∠C=60°,那么∠E=____ 度,∠EDF=_______度,∠F=______度,∠DOB=_______度.
3.如图所示,长方体中,平移后能得到棱AA1的棱有________.
4.小明的一本书一共有104页,在这104页的页码中有两个数码的,并且这两个数 码经过平移其中一个能得到另一个,则这样的页共有________页.
三、训练平台:(每小题5分,共15分)
1.如图所示,请将图中的“蘑菇”向左平移6个格,再向下平移2个格.
(第1题) (第2题) (第3题)
2.如图所示,将△ABC平移,可以得到△DEF,点B的对应点为点E,请画出点A的对 应点D、点C的对应点F的位置.
3.如图所示,画出平行四边形ABCD向上平移1厘米后的图形.
四、提高训练:(每小题6分,共12分)
1.如图所示的是某商品包装盒上图案的一部分,请分析这个图案的基本图形 和形成过程.
2.如图所示,四边形ABCD中,AD∥BC,AB=DC=AD,将DC向左平移AD长,平移后你 得到的两个图形是什么样的
五、探索发现:(共8分)
公路上同向而行的两辆汽车,从后车车头与前车车尾“相遇”到原后车车尾离 开原车车头这段时间为超车时间,如果原前、后两车车长分别为a,b,那么在超车时 间内两车行驶的路程与两车车长有何关系
六、能力提高:(每小题9分,共18分)
1.如图所示,四边形ABCD中,AD∥BC,AB=DC,∠B=80°,求∠A,∠D,∠C的度数.
2.如图所示,大圆O内有一小圆O1,小圆O1从现在的位置沿O1O的方向平移4个 单位后,得到小圆O2,已知小圆半径为1.
(1)求大圆的面积;(2)求小圆在平移过程中扫过的面积.
七、中考题与竞赛题:(每小题10分,共20分)
1.(2013.福建)如图14所示,点A,B,C,D在同一条直线上,AB=CD,∠D=∠ECA,EC= FD.试说明AE=BF.
2.如图15所示的是用火柴杆摆的一只向左飞行的小鸟,你能只平移3根火柴杆就 使它向右飞吗
参考答案:
一、1.A 2.D 3.C 4.C 5.C
二、1.形状 大小 相等 2.70 50 60 60 3.BB1,CC1,DD1 4.9
三、1.提示:先画出主要点的对应点,然后再连线.
2.提示:过点E作BA,BC的平行线,再截取DE=AB,FE=CB.
3.略
四、1.提示:基本图形是 ,由这个图形平移得到.
2.如图7所示,△ABC′是等腰三角形,四边形AC′CD是菱形.
五、解:如图8所示,两车行驶的路程即平移的距离,从图中很容易看出:在超车 时间内两车的路程差等于a+b.
六、1.解:将CD沿DA方向平移DA长(如图9所示),显然BA=CD=EA,所以△ABE是等 腰三角形,∠AEB=∠B=80°,又AE∥CD,∴∠C=∠AEB=80°,又AD∥BC,∴∠D+∠C=18 0°,∠D=100°,同理可得∠BAD=100°.
2.解:(1)根据平移知识可知MN=4(如图10所示),又∵小圆半径为1,∴大圆直 径PN=大圆面积为 =;
(2)小圆平移时扫过的面积为长方形ABCD的面积+小圆面积 =2×4+.
七、1.提示:根据已知条件可知,将△AEC平移后可得到△BFD,根据对应线段相 等,可得AE=BF.
2.解:如图11所示.毛
