【新课标】1.2二次函数的图象与性质(3) 课件(共30张PPT)
文档属性
| 名称 | 【新课标】1.2二次函数的图象与性质(3) 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-20 15:07:28 | ||
图片预览









文档简介
(共30张PPT)
1.2二次函数的图象与性质(3)
湘教版 九年级下
教学内容分析
本节内容从二次函数y=ax2 迁移过来,理解平移可以得到y=a(x-h)2的图象,按照顶点、对称轴、开口方向来研究二次函数y=a(x-h)2 的图象与性质,在二次函数章节中具有重要地位。
教学目标
1.理解二次函数y=ax2 平移得到y=a(x-h)2。
2.理解二次函数y=a(x-h)2 的图象与性质(重点)
3.熟练地画出二次函数y=a(x-h)2 的图象(难点)
核心素养分析
学生总结画二次函数y=ax2图象的步骤之后,经历推导y=a(x-h)2的图象的过程,加深了学生对画图的认知,继续培养对平移的理解,提升画图象的能力和思维水平,锻炼了学生动手操作的能力,提高了对数形结合的思想的认识。
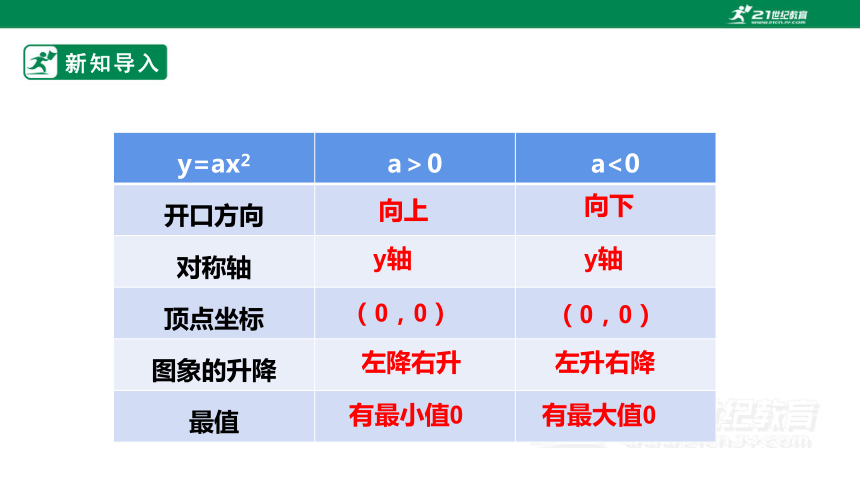
新知导入
y=ax2 a>0 a<0
开口方向
对称轴
顶点坐标
图象的升降
最值
左降右升
左升右降
(0,0)
(0,0)
有最小值0
有最大值0
y轴
y轴
向上
向下
新知讲解
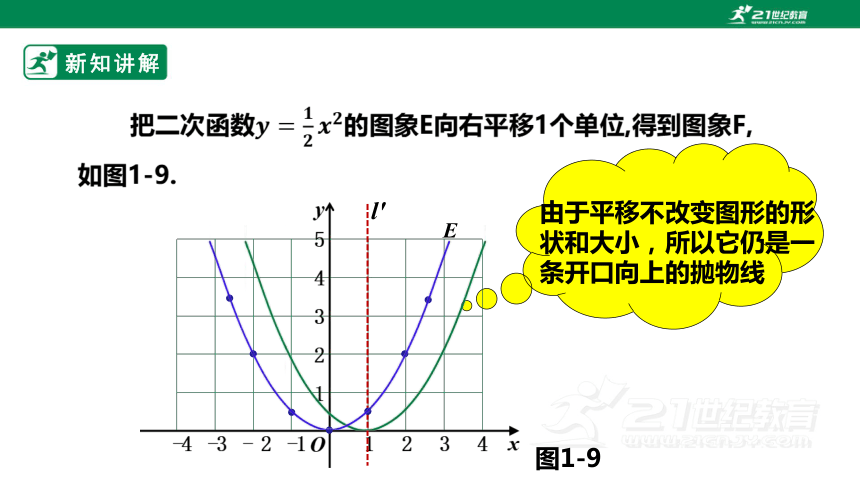
把二次函数的图象E向右平移1个单位,得到图象F,如图1-9.
l′
E
由于平移不改变图形的形状和大小,所以它仍是一条开口向上的抛物线
图1-9
新知讲解
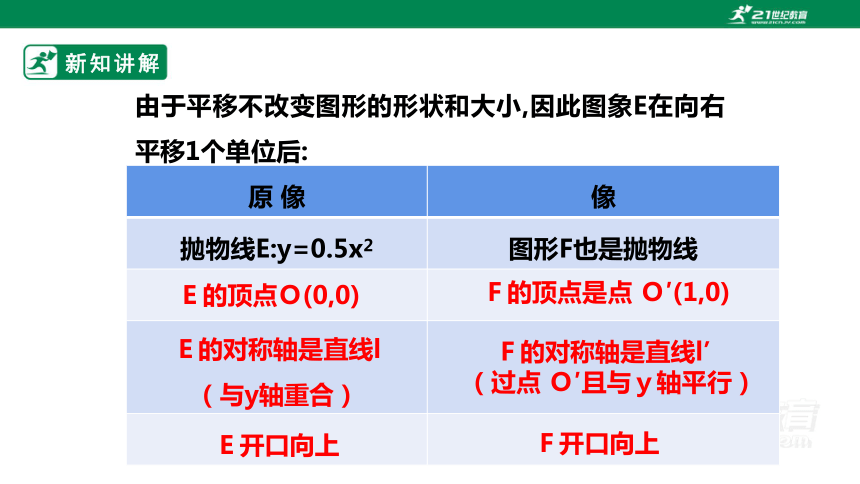
由于平移不改变图形的形状和大小,因此图象E在向右平移1个单位后:
原 像 像
抛物线E:y=0.5x2 图形F也是抛物线
E的顶点O(0,0)
F的顶点是点 O′(1,0)
E的对称轴是直线l(与y轴重合)
F的对称轴是直线l’
(过点 O′且与y轴平行)
E开口向上
F开口向上
新知讲解
抛物线F是哪个函数的图象呢?
在抛物线 的图象上任取一点P ,那么在向右平移 1个单位后, 点P的像点Q的坐标是什么?
把点P的横坐标a加上1,纵坐标0.5a2不变, 就得到像点Q的坐标为(a+1,0.5a2) 。
新知讲解
记b=a+1,则a=b-1,
从而点Q的坐标为 ".
这表明:点Q在函数的图象上.
由此得出,抛物线F是函数 的图象.
新知讲解
函数 的图象特点:
它的开口向上,顶点是O′(1,0),
对称轴是过点 O′(1,0) 且平行于y轴的直线l’.
直线l’是由横坐标为1的所有点组成的,
我们把直线l’记作直线x=1.
新知讲解
二次函数y=a(x-h)2的图象是抛物线,它的对称轴是直线 x=h,它的顶点坐标是(h,0). 当a>0时,抛物线的开口向上; 当 a<0时,抛物线的开口向下.
新知讲解
画y=a(x-h)2的图象时:
1、只要先画出对称轴以及图象在对称轴右边的部分,
2、然后利用对称性,画出图象在对称轴左边的部分.
3、在画图象的右边部分时,只需”列表、描点、连线”三个步骤。
新知讲解
例3 画函数y=(x-2)2的图象.
解 抛物线y=(x-2)2的对称轴是直线x=2,顶点坐标是(2,0).
列表:自变量x从顶点的横坐标2开始取值.
x ...
y=(x-2)2 ...
2
0
3
1
4
4
5
9
新知讲解
描点和连线:
画出图象在对称轴右边的部分.
利用对称性,画出图象在对称轴左边的部分.
这样就得到了y=(x-2)2的图象,如图1-10.
图1-10
-2
10
8
6
4
2
2 4 6
O
x
y
对称轴x=2
新知讲解
二次函数
开口方向
对称轴
顶点坐标
增减性
y=a(x-h)2
直线x=h
(h,0)
a>0,左降右升
a<0,左升右降
a>0,抛物线的开口向上;
a<0,抛物线的开口向下
二次函数左右平移“四字诀”
(1)左负右正:
由y=ax2平移到y = a(x-h)2时符合h左负右正(h >0,向右平移, h<0,向左平移).
(2)左正右负:
由y= ax2平移到y = a(x+h )2时符合h左正右负.
新知讲解
E
y = ax2
y = a(x-h)2
课堂练习
1.二次函数y=(x-3)2的顶点坐标,开口方向,对称轴分别是?
解:因为y=(x-3)2是抛物线的顶点式,
根据顶点式的坐标特点,顶点坐标为(3,0).
开口向上,对称轴是x=3.
课堂练习
2. 关于抛物线y=(x-5)2,下列说法错误的是( )
A. 开口向上 B. 当x>5时,y随x的增大而减小
C. 对称轴是直线x=5 D. 顶点(5,0)
B
课堂练习
解:∵抛物线y=(x-5)2,
A、因为a=1>0,开口向上,故说法正确,不符合题意;
B、当x>5时,y随x的增大而增大,故说法错误,符合题意;
C、因为对称轴是直线x=5,故说法正确,不符合题意;
D、因为顶点为(5,0),故说法正确,不符合题意;
课堂练习
3.将抛物线y=x2-3向左平移2个单位后得到的抛物线
表达式是( )
A. y=x2-1 B. y=x2-5
C. y=(x+2)2-3 D. y=(x-2)2-3
C
课堂练习
解:将抛物线y=x2-3向左平移2个单位后
得到的抛物线表达式是y=(x+2)2-3.
故选:C.
按照“左加右减”的规律,即可得出平移后抛物线的解析式.
课堂练习
4.已知抛物线y=-(x+1)2上的两点A(x1,y1),B(x2,y2),
如果x1A. y1A
课堂练习
解:∵A(x1,y1),B(x2,y2)在抛物线y=-(x+1)2上,
a=-1<0,开口向下,
对称轴x=-1,
顶点坐标(-1,0),
在对称轴左侧,y随x的增大而增大。
∴当x1故选:A.
课堂练习
5.二次函数y=a(x-h)2的图象如图所示,若A(-2,y1),B(-4,y2)
是该图象上的两点,则y1_____y2.(填“>”“<”或“=”)
=
课堂练习
解:∵抛物线的对称轴为直线x=-3,
∵-2与-4关于对称轴x=-3对称,
∴y1=y2.
故答案为:=
课堂总结
二次函数的
图象与性质
2.二次函数y=a(x-h)2图象的性质:
顶点(h,0)
关于x=h对称,
a>0,左降右升
a<0,左升右降
1. 画二次函数y=a(x-h)2的图象
板书设计
1.2二次函数y=a(x-h)2的图象与性质
1.画二次函数y=a(x-h)2的步骤:列表、描点、连线
2.二次函数y=a(x-h)2的图象与性质
作业布置
必做题:课本第12页练习的第1,2题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.2二次函数的图象与性质(3)
湘教版 九年级下
教学内容分析
本节内容从二次函数y=ax2 迁移过来,理解平移可以得到y=a(x-h)2的图象,按照顶点、对称轴、开口方向来研究二次函数y=a(x-h)2 的图象与性质,在二次函数章节中具有重要地位。
教学目标
1.理解二次函数y=ax2 平移得到y=a(x-h)2。
2.理解二次函数y=a(x-h)2 的图象与性质(重点)
3.熟练地画出二次函数y=a(x-h)2 的图象(难点)
核心素养分析
学生总结画二次函数y=ax2图象的步骤之后,经历推导y=a(x-h)2的图象的过程,加深了学生对画图的认知,继续培养对平移的理解,提升画图象的能力和思维水平,锻炼了学生动手操作的能力,提高了对数形结合的思想的认识。
新知导入
y=ax2 a>0 a<0
开口方向
对称轴
顶点坐标
图象的升降
最值
左降右升
左升右降
(0,0)
(0,0)
有最小值0
有最大值0
y轴
y轴
向上
向下
新知讲解
把二次函数的图象E向右平移1个单位,得到图象F,如图1-9.
l′
E
由于平移不改变图形的形状和大小,所以它仍是一条开口向上的抛物线
图1-9
新知讲解
由于平移不改变图形的形状和大小,因此图象E在向右平移1个单位后:
原 像 像
抛物线E:y=0.5x2 图形F也是抛物线
E的顶点O(0,0)
F的顶点是点 O′(1,0)
E的对称轴是直线l(与y轴重合)
F的对称轴是直线l’
(过点 O′且与y轴平行)
E开口向上
F开口向上
新知讲解
抛物线F是哪个函数的图象呢?
在抛物线 的图象上任取一点P ,那么在向右平移 1个单位后, 点P的像点Q的坐标是什么?
把点P的横坐标a加上1,纵坐标0.5a2不变, 就得到像点Q的坐标为(a+1,0.5a2) 。
新知讲解
记b=a+1,则a=b-1,
从而点Q的坐标为 ".
这表明:点Q在函数的图象上.
由此得出,抛物线F是函数 的图象.
新知讲解
函数 的图象特点:
它的开口向上,顶点是O′(1,0),
对称轴是过点 O′(1,0) 且平行于y轴的直线l’.
直线l’是由横坐标为1的所有点组成的,
我们把直线l’记作直线x=1.
新知讲解
二次函数y=a(x-h)2的图象是抛物线,它的对称轴是直线 x=h,它的顶点坐标是(h,0). 当a>0时,抛物线的开口向上; 当 a<0时,抛物线的开口向下.
新知讲解
画y=a(x-h)2的图象时:
1、只要先画出对称轴以及图象在对称轴右边的部分,
2、然后利用对称性,画出图象在对称轴左边的部分.
3、在画图象的右边部分时,只需”列表、描点、连线”三个步骤。
新知讲解
例3 画函数y=(x-2)2的图象.
解 抛物线y=(x-2)2的对称轴是直线x=2,顶点坐标是(2,0).
列表:自变量x从顶点的横坐标2开始取值.
x ...
y=(x-2)2 ...
2
0
3
1
4
4
5
9
新知讲解
描点和连线:
画出图象在对称轴右边的部分.
利用对称性,画出图象在对称轴左边的部分.
这样就得到了y=(x-2)2的图象,如图1-10.
图1-10
-2
10
8
6
4
2
2 4 6
O
x
y
对称轴x=2
新知讲解
二次函数
开口方向
对称轴
顶点坐标
增减性
y=a(x-h)2
直线x=h
(h,0)
a>0,左降右升
a<0,左升右降
a>0,抛物线的开口向上;
a<0,抛物线的开口向下
二次函数左右平移“四字诀”
(1)左负右正:
由y=ax2平移到y = a(x-h)2时符合h左负右正(h >0,向右平移, h<0,向左平移).
(2)左正右负:
由y= ax2平移到y = a(x+h )2时符合h左正右负.
新知讲解
E
y = ax2
y = a(x-h)2
课堂练习
1.二次函数y=(x-3)2的顶点坐标,开口方向,对称轴分别是?
解:因为y=(x-3)2是抛物线的顶点式,
根据顶点式的坐标特点,顶点坐标为(3,0).
开口向上,对称轴是x=3.
课堂练习
2. 关于抛物线y=(x-5)2,下列说法错误的是( )
A. 开口向上 B. 当x>5时,y随x的增大而减小
C. 对称轴是直线x=5 D. 顶点(5,0)
B
课堂练习
解:∵抛物线y=(x-5)2,
A、因为a=1>0,开口向上,故说法正确,不符合题意;
B、当x>5时,y随x的增大而增大,故说法错误,符合题意;
C、因为对称轴是直线x=5,故说法正确,不符合题意;
D、因为顶点为(5,0),故说法正确,不符合题意;
课堂练习
3.将抛物线y=x2-3向左平移2个单位后得到的抛物线
表达式是( )
A. y=x2-1 B. y=x2-5
C. y=(x+2)2-3 D. y=(x-2)2-3
C
课堂练习
解:将抛物线y=x2-3向左平移2个单位后
得到的抛物线表达式是y=(x+2)2-3.
故选:C.
按照“左加右减”的规律,即可得出平移后抛物线的解析式.
课堂练习
4.已知抛物线y=-(x+1)2上的两点A(x1,y1),B(x2,y2),
如果x1
课堂练习
解:∵A(x1,y1),B(x2,y2)在抛物线y=-(x+1)2上,
a=-1<0,开口向下,
对称轴x=-1,
顶点坐标(-1,0),
在对称轴左侧,y随x的增大而增大。
∴当x1
课堂练习
5.二次函数y=a(x-h)2的图象如图所示,若A(-2,y1),B(-4,y2)
是该图象上的两点,则y1_____y2.(填“>”“<”或“=”)
=
课堂练习
解:∵抛物线的对称轴为直线x=-3,
∵-2与-4关于对称轴x=-3对称,
∴y1=y2.
故答案为:=
课堂总结
二次函数的
图象与性质
2.二次函数y=a(x-h)2图象的性质:
顶点(h,0)
关于x=h对称,
a>0,左降右升
a<0,左升右降
1. 画二次函数y=a(x-h)2的图象
板书设计
1.2二次函数y=a(x-h)2的图象与性质
1.画二次函数y=a(x-h)2的步骤:列表、描点、连线
2.二次函数y=a(x-h)2的图象与性质
作业布置
必做题:课本第12页练习的第1,2题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
