湘教版2022-2023学年度八年级上学期期末练习数学试题4(含解析)
文档属性
| 名称 | 湘教版2022-2023学年度八年级上学期期末练习数学试题4(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-20 14:33:17 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
湘教版2022-2023学年八年级上学期期末练习试题4
姓名:__________班级:__________考号:__________总分__________
1 、选择题
下列分式中,最简分式是( )
A. B. C. D.
若++1在实数范围内有意义,则x满足的条件是( )
A.x≥ B.x≤ C.x= D.x≠
如图,为估计南开中学桃李湖岸边A.B两点之间的距离,小华在湖的一侧选取一点O,测得OA=15米,OB=10米,则A.B间的距离可能是( )
A.5米 B.15米 C.25米 D.30米
在中,,平分,交于点,,垂足为点,若,则的长为( )
A.3 B. C.2 D.6
边长为2的正方形的面积是4,边长为3的正方形的面积是9,则面积是6的正方形的边长a满足( )
A.a是整数 B.2<a<3
C.2<a<3,且a为分数 D.a不存在
不等式>x的解为( )
A.x<1 B.x<﹣1 C.x>1 D.x>﹣1
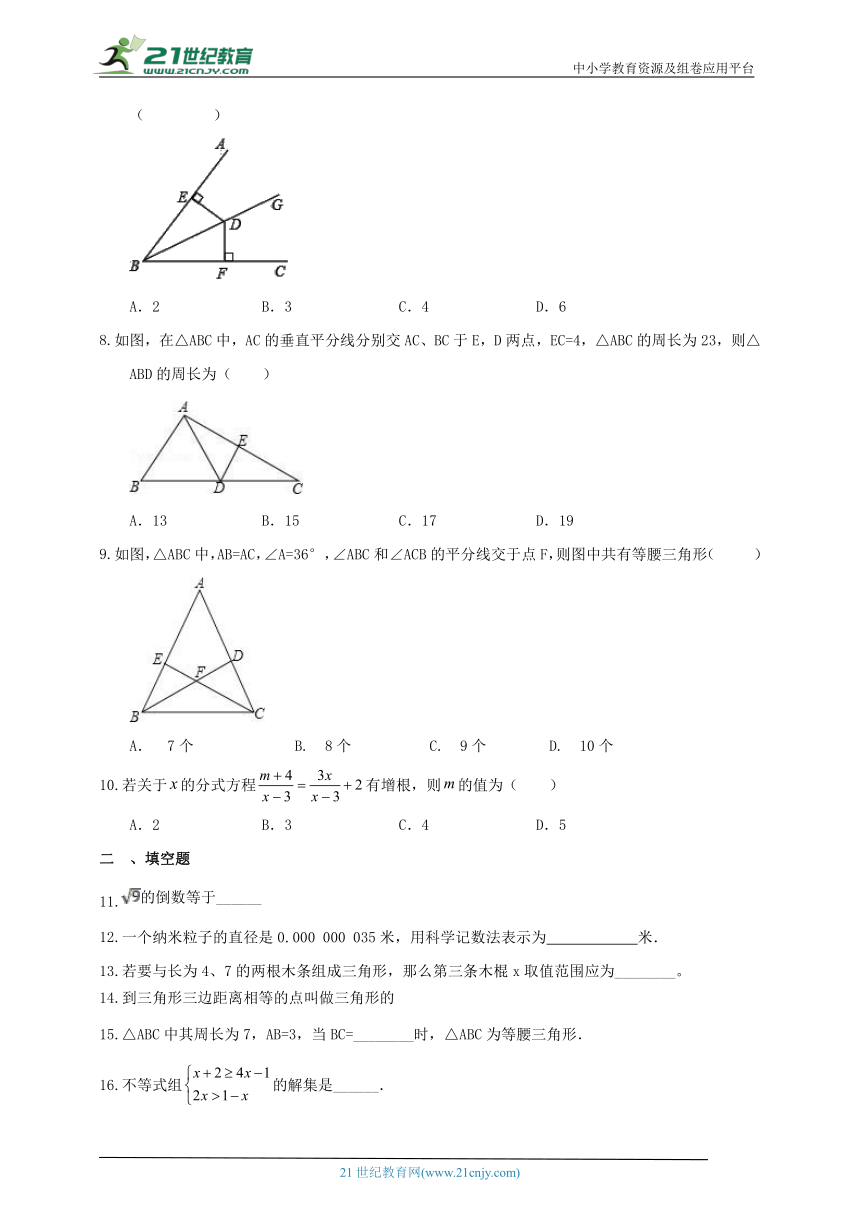
如图,已知 BG 是∠ABC 的平分线,DE⊥AB 于点 E,DF⊥BC 于点 F,DE=6,则 DF 的长度是( )
A.2 B.3 C.4 D.6
如图,在△ABC中,AC的垂直平分线分别交AC、BC于E,D两点,EC=4,△ABC的周长为23,则△ABD的周长为( )
A.13 B.15 C.17 D.19
如图,△ABC中,AB=AC,∠A=36°,∠ABC和∠ACB的平分线交于点F,则图中共有等腰三角形( )
A. 7个 B. 8个 C. 9个 D. 10个
若关于的分式方程有增根,则的值为( )
A.2 B.3 C.4 D.5
1 、填空题
的倒数等于______
一个纳米粒子的直径是0.000 000 035米,用科学记数法表示为 米.
若要与长为4、7的两根木条组成三角形,那么第三条木棍x取值范围应为________。
到三角形三边距离相等的点叫做三角形的
△ABC中其周长为7,AB=3,当BC=________时,△ABC为等腰三角形.
不等式组的解集是______.
如图,直线,点在直线上,点在直线上,,,,则______.
已知,化简得____________.
1 、解答题
先化简,再求值:,其中.
解不等式组
已知:如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°.
求证:AO=BO,CO=DO.
某商场的运动服装专柜,对A,B两种品牌的运动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如下表:
第一次 第二次
A品牌运动服装数/件 20 30
B品牌运动服装数/件 30 40
累计采购款/元 10200 14400
(1)问A,B两种品牌运动服的进货单价各是多少元?
(2)由于B品牌运动服的销量明显好于A品牌,商家决定采购B品牌的件数比A品牌件数的倍多5件,在采购总价不超过21300元的情况下,最多能购进多少件B品牌运动服?
(1)探索:先观察并计算下列各式,在空白处填上“>”、“<”或“=”,并完成后面的问题.
× ,× ,× ,× …
用,,表示上述规律为: ;
(2)利用(1)中的结论,求×的值
(3)设x=,y=试用含x,y的式子表示.
为了尽快实施“脱贫致富奔小康”宏伟意图,某县扶贫工作队为朝阳沟村购买了一批苹果树苗和梨树苗,已知一棵苹果树苗比一棵梨树苗贵2元,购买苹果树苗的费用和购买梨树苗的费用分别是3500元和2500元.
(1)若两种树苗购买的棵数一样多,求梨树苗的单价;
(2)若两种树苗共购买1100棵,且购买两种树苗的总费用不超过6000元,根据(1)中两种树苗的单价,求梨树苗至少购买多少棵.
如图所示,在不等边中,,,的垂直平分线交边于点,交边于点,垂直平分线交边于点,交边于点.
(1)若,求的度数;
(2)若边长为整数,求的周长.
△ABC和△ADE都是等边三角形.
(1)将△ADE绕点A旋转到图①的位置时,连接BD,CE并延长相交于点P(点P与点A重合),有PA+PB=PC(或PA+PC=PB)成立(不需证明),
(2)将△ADE绕点A旋转到图②的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA.PB、PC之间有怎样的数量关系?并加以证明,
(3)将△ADE绕点A旋转到图③的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA.PB、PC之间有怎样的数量关系?直接写出结论,不需要证明.
答案解析
1 、选择题
【考点】最简分式
【分析】最简分式的标准是分子,分母中不含有公因式,不能再约分.判断的方法是把分子、分母分解因式,并且观察有无互为相反数的因式,这样的因式可以通过符号变化化为相同的因式从而进行约分.
解:A. 符合最简分式;
B、不符合最简分式,
C. =不符合最简分式,
D. =不符合最简分式.
故选A.
【点评】此题考查最简分式问题,分式的化简过程,首先要把分子分母分解因式,互为相反数的因式是比较易忽视的问题.在解题中一定要引起注意.
【考点】二次根式有意义的条件.
【分析】根据二次根式有意义的条件即可求出x的值.
解:由题意可知:
解得:x=
故选C
【点评】本题考查二次根式有意义的条件,解题的关键是正确理解二次根式有意义的条件,本题属于基础题型。
【考点】三角形三边关系.
【分析】本题是一个三角形第三边取值范围的题,第三边值在其他两边之和,和两边之差之间.
解:依题意,在三角形AOB中,
OA﹣OB<AB<OA+OB,OA=15米,OB=10米,
即5米<AB<25米.
所以15米符合题意.
故选B.
【点评】本题考查了三角形三边关系,第三边的在范围中选得.
【考点】全等三角形的判定和性质,角平分线的性质
【分析】证明△ABD≌△AED即可得出DE的长.
解:∵DE⊥AC,
∴∠AED=∠B=90°,
∵AD平分∠BAC,
∴∠BAD=∠EAD,
又∵AD=AD,
∴△ABD≌△AED,
∴DE=BE=3,
故选:A.
【点评】本题考查了全等三角形的判定和性质,角平分线的性质,掌握全等三角形的判定定理是解题关键.
【考点】估算无理数的大小
【分析】由正方形的面积等于边长的平方,可得到a2=6,∵4<6<9,∴22<a2<32,即:2<a<3.
解:∵正方形的面积等于边长的平方,
∴a2=6,
∵4<6<9,
∴22<a2<32,
即:2<a<3.
故选:B.
【点评】本题考查了估算无理数的大小,解题的关键是找出和6左右最接近的两个能完全开方的数.
【考点】解一元一次不等式
【分析】去分母、移项,合并同类项,系数化成1即可.
解:>x,
3﹣x>2x,
3>3x,
x<1,
故选:A.
【点评】本题考查了解一元一次不等式,注意:解一元一次不等式的步骤是:去分母、去括号、移项、合并同类项、系数化成1.
【考点】角平分线的性质
【分析】根据角的平分线上的点到角的两边的距离相等即可得.
解:∵BG 是∠ABC 的平分线,DE⊥AB,DF⊥BC,
∴DE=DF=6, 故选:D.
【点评】本题主要考查角平分线的性质,解题的关键是掌握角的平分线上的点到 角的两边的距离相等.
【考点】线段垂直平分线的性质.
【分析】根据线段垂直平分线性质得出AD=DC,AE=CE=4,求出AC=8,AB+BC=15,求出△ABD的周长为AB+BC,代入求出即可.
解:∵AC的垂直平分线分别交AC、BC于E,D两点,
∴AD=DC,AE=CE=4,
即AC=8,
∵△ABC的周长为23,
∴AB+BC+AC=23,
∴AB+BC=23﹣8=15,
∴△ABD的周长为AB+BD+AD=AB+BD+CD=AB+BC=15,
故选B.
【点评】本题考查了线段垂直平分线性质的应用,能熟记线段垂直平分线性质定理的内容是解此题的关键,注意:线段垂直平分线上的点到线段两个端点的距离相等.
【考点】等腰三角形的判定与性质,三角形内角和定理,三角外角的性质
【分析】由在△ABC中,AB=AC,∠A=36°,根据等边对等角,即可求得∠ABC与∠ACB的度数,又由BD、CE分别为∠ABC与∠ACB的角平分线,即可求得∠ABD=∠CBD=∠ACE=∠BCE=∠A=36°,然后利用三角形内角和定理与三角形外角的性质,即可求得∠BEF=∠BFE=∠ABC=∠ACB=∠CDF=∠CFD=72°,由等角对等边,即可求得答案.
解:∵在△ABC中,AB=AC,∠A=36°, ∴∠ABC=∠ACB= =72°,
∵BD、CE分别为∠ABC与∠ACB的角平分线,
∴∠ABD=∠CBD=∠ACE=∠BCE=∠A=36°,
∴AE=CE,AD=BD,BF=CF,
∴△ABC,△ABD,△ACE,△BFC是等腰三角形,
∵∠BEC=180°﹣∠ABC﹣∠BCE=72°,∠CDB=180°﹣∠BCD﹣∠CBD=72°,∠EFB=∠DFC=∠CBD+∠BCE=72°,
∴∠BEF=∠BFE=∠ABC=∠ACB=∠CDF=∠CFD=72°,
∴BE=BO,CF=CD,BC=BD=CF,
∴△BEF,△CDF,△BCD,△CBE是等腰三角形.
∴图中的等腰三角形有8个.
故选B.
【点评】本题考查了等腰三角新的判定与性质、三角形内角和定理以及三角外角的性质.此题难度不大,解题的关键是求得各角的度数,掌握等角对等边与等边对等角定理的应用.
【考点】分式方程的增根
【分析】根据分式方程有增根可求出,方程去分母后将代入求解即可.
解:∵分式方程有增根,
∴,
去分母,得,
将代入,得,
解得.
故选:D.
【点评】本题考查了分式方程的无解问题,掌握分式方程中增根的定义及增根产生的原因是解题的关键.
1 、填空题
【考点】实数的性质
【分析】先化简,再求倒数即可.
解:∵=3,
∴的倒数等于.
【点评】本题考查了算术平方根的意义及倒数的定义,根据算术平方根的定义正确化简是解答本题的关键.
【考点】科学记数法—表示较小的数.
【分析】绝对值小于1的数也可以利用科学记数法表示,一般形式为a×10﹣n,与绝对值大于1数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
解:0.000 000 035=3.5×10﹣8.
故答案是:3.5×10﹣8.
【点评】本题考查用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
【考点】三角形三条边的关系
【分析】根据三角形的三边关系解答即可.
解:∵要与长为4、7的两根木条组成三角形,
∴7-4故答案为:3【点评】本题考查三角形三边的关系,三角形任意两边之和大于第三边,任意两边之差小于第三边,熟练掌握三角形三边的关系是解题关键.
【考点】三角形的内心
【分析】根据三角形的内心的定义直接写出答案
解:到三角形三边距离相等的点是三条角平分线的交点,叫做三角形的内心
答案:内心
【点评】本题考查了三角形的内心,熟记定义是关键。
【考点】等腰三角形的判定
【分析】由于等腰三角形的两腰相等,题目给出了周长,根据三角形的条件即可求解.
解:因为△ABC中其周长为7,AB=3,
设AB为腰,BC为底时,则BC=7﹣3﹣3=1,可构成三角形;
设AB为腰,BC为腰时,则BC=3,可构成三角形。
设AB为底,则BC= ,可构成三角形;
故答案为:1或2或3
【点评】此题考查了等腰三角形两腰相等的性质,关键是根据三角形的条件解答.
【考点】解一元一次不等式组
【分析】分别求出两个不等式的解集,再找出两个解集的公共部分即可得答案.
解:
解不等式得:,
解不等式得:,
∴不等式组的解集是,
故答案为:
【点评】本题考查解一元一次不等式组,正确得出两个不等式的解集是解题关键.
【考点】等腰三角形的性质,平行线的性质,三角形内角和定理
【分析】利用等腰三角形的性质得到∠C=∠4=,利用平行线的性质得到∠1=∠3=,再根据三角形内角和定理即可求解.
解:如图,延长CB交于点D,
∵AB=BC,∠C=,
∴∠C=∠4=,
∵,∠1=,
∴∠1=∠3=,
∵∠C +∠3+∠2+∠4 =,即
∴
故答案为:.
【点评】本题考查了等腰三角形的性质,平行线的性质以及三角形内角和定理的应用,解决问题的关键是辅助线的作法,注意运用两直线平行,同位角相等.
【考点】二次根式的性质与化简
【分析】根据完全平方公式结合二次根式的性质进行化简即可求得答案.
解:∵0∴>1,
∴
=
=
=,
故答案为:.
【点评】本题考查了二次根式的性质与化简,熟练掌握完全平方公式的结构特征是解本题的关键.
1 、解答题
【考点】分式的化简求值
【分析】第一个小括号,先通分再求和,结合平方差公式、完全平方公式将因式分解成,再将分式的除法转化为乘法运算,约分化简,最后代入数值计算即可.
解:
当时,
原式
.
【点评】本题考查分式的化简求值,涉及平方差、完全平方公式等因式分解法,是重要考点,难度较易,掌握相关知识是解题关键.
【考点】解一元一次不等式组
【分析】分别解出每个不等式的解,再得出不等式组的解集.
解: ,
解不等式①得:x>-1,
解不等式②得:x<2,
∴不等式组的解集为:-1【考点】全等三角形的性质和判定
【分析】根据HL证明Rt△ACB≌Rt△ADB,得∠ABC=∠BAD,根据等角对等边,得OA=OB,所以,由AD﹣OA=BC﹣OB,得OD=OC.
证明:∵∠C=∠D=90°,
∴△ACB和△ADB为直角三角形,
在Rt△ACB和Rt△ADB中,
,
∴Rt△ACB≌Rt△ADB,
∴∠ABC=∠BAD,
∴OA=OB,
∵AD=BC,
∴AD﹣OA=BC﹣OB,
即OD=OC.
【点评】本题考核知识点:全等三角形,等腰三角形. 解题关键点:运用全等三角形的性质和等腰三角形性质证明线段相等.
【考点】二元一次方程组的应用,一元一次不等式的应用
【分析】(1)直接利用两次采购的总费用得出等式进而得出答案,
(2)利用采购B品牌的件数比A品牌件数的倍多5件,在采购总价不超过21300元,进而得出不等式求出答案.
解:(1)设A,B两种品牌运动服的进货单价各是x元和y元,根据题意可得:
,
解得:,
答:A,B两种品牌运动服的进货单价各是240元和180元,
(2)设购进A品牌运动服m件,购进B品牌运动服(m+5)件,
则240m+180(m+5)≤21300,
解得:m≤40,
经检验,不等式的解符合题意,
∴m+5≤×40+5=65,
答:最多能购进65件B品牌运动服.
【点评】此题主要考查了一元一次不等式的应用和二元一次方程组的应用,正确得出等量关系是解题关键.
【考点】二次根式的乘除法
【分析】(1)先求出每个式子的值,再比较即可;
(2)根据规律,把被开方数相乘,根指数不变,即可求出答案;
(3)先分解质因数,再根据规律得出,即可得出答案.
解:(1)∵×=2×4=8,==8,
∴×=,
×=,
×=
×=,
故答案为:=,=,=,=, =(a≥0,b≥0);
(2)×
=
=
=2;
(3)∵x=,y=,
∴=
=
=x x y
=x2y.
【点评】本题考查了二次根式的乘除,能根据求出的结果得出规律是解此题的关键.
【考点】分式方程的应用;一元一次不等式的应用.
【分析】(1)设梨树苗的单价为x元,则苹果树苗的单价为(x+2)元,根据两种树苗购买的棵树一样多列出方程求出其解即可;
(2)设购买梨树苗种树苗a棵,苹果树苗则购买棵,根据购买两种树苗的总费用不超过6000元建立不等式求出其解即可.
解:(1)设梨树苗的单价为x元,则苹果树苗的单价为(x+2)元,
依题意得: =,
解得x=5.
经检验x=5是原方程的解,且符合题意.
答:梨树苗的单价是5元;
(2)设购买梨树苗种树苗a棵,苹果树苗则购买棵,
依题意得:(5+2)+5a≤6000,
解得a≥850.
答:梨树苗至少购买850棵.
【点评】本题考查了列分式方程解实际问题的运用,一元一次不等式解实际问题的运用,解答时由方程求出两种树苗的单价是关键.
【考点】线段垂直平分线的性质,三角形三边关系,三角形内角和定理
【分析】(1)根据垂直平分线的性质得到和,再根据三角形内角和去算出角的度数;
(2)根据三角形三边关系求出BC长,再根据垂直平分线的性质证明的周长等于BC的长.
解:(1)∵DE、MN分别是线段AB和线段AC的垂直平分线,
∴AE=BE,AN=CN,
∴,,
∵,
∴,
∴;
(2)在中,,即,
∵BC边长是整数,
∴BC的长度可以取2、3、4,
∵是不等边的,
∴BC=4,
由(1)知AE=BE,AN=CN,
∴.
【点评】本题考查垂直平分线的性质,三角形三边关系和内角和,解题的关键是掌握垂直平分线的性质.
【考点】全等三角形的判定与性质,等边三角形的判定与性质.
【分析】(2)证明△ABD≌△ACE(SAS)和△BAF≌△CAP(SAS),得AF=AP,∠BAF=∠CAP,再证明△AFP是等边三角形,最后由线段的和可得结论,
(3)如图③,在PC上截取CM=PB,连接AM,同理可得结论.
解:(2)PB=PA+PC,理由如下:
如图②,在BP上截取BF=PC,连接AF,
∵△ABC、△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAC+∠CAD=∠CAD+∠DAE,
即∠DAB=∠EAC,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∵AB=AC,BF=CP,
∴△BAF≌△CAP(SAS),
∴AF=AP,∠BAF=∠CAP,
∴∠BAC=∠PAF=90°,
∴△AFP是等边三角形,
∴PF=PA,
∴PB=BF+PF=PC+PA,
(3)PC=PA+PB,理由如下:
如图③,在PC上截取CM=PB,连接AM,
同理得:△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∵AB=AC,PB=CM,
∴△AMC≌△APB(SAS),
∴AM=AP,∠BAP=∠CAM,
∴∠BAC=∠PAM=60°,
∴△AMP是等边三角形,
∴PM=PA,
∴PC=PM+CM=PA+PB.
【点评】本题考查了等边三角形的性质、全等三角形的判定与性质等知识,熟练掌握等边三角形的性质,证明△ABD≌△ACE是解题的关键,属于中考常考题型.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
湘教版2022-2023学年八年级上学期期末练习试题4
姓名:__________班级:__________考号:__________总分__________
1 、选择题
下列分式中,最简分式是( )
A. B. C. D.
若++1在实数范围内有意义,则x满足的条件是( )
A.x≥ B.x≤ C.x= D.x≠
如图,为估计南开中学桃李湖岸边A.B两点之间的距离,小华在湖的一侧选取一点O,测得OA=15米,OB=10米,则A.B间的距离可能是( )
A.5米 B.15米 C.25米 D.30米
在中,,平分,交于点,,垂足为点,若,则的长为( )
A.3 B. C.2 D.6
边长为2的正方形的面积是4,边长为3的正方形的面积是9,则面积是6的正方形的边长a满足( )
A.a是整数 B.2<a<3
C.2<a<3,且a为分数 D.a不存在
不等式>x的解为( )
A.x<1 B.x<﹣1 C.x>1 D.x>﹣1
如图,已知 BG 是∠ABC 的平分线,DE⊥AB 于点 E,DF⊥BC 于点 F,DE=6,则 DF 的长度是( )
A.2 B.3 C.4 D.6
如图,在△ABC中,AC的垂直平分线分别交AC、BC于E,D两点,EC=4,△ABC的周长为23,则△ABD的周长为( )
A.13 B.15 C.17 D.19
如图,△ABC中,AB=AC,∠A=36°,∠ABC和∠ACB的平分线交于点F,则图中共有等腰三角形( )
A. 7个 B. 8个 C. 9个 D. 10个
若关于的分式方程有增根,则的值为( )
A.2 B.3 C.4 D.5
1 、填空题
的倒数等于______
一个纳米粒子的直径是0.000 000 035米,用科学记数法表示为 米.
若要与长为4、7的两根木条组成三角形,那么第三条木棍x取值范围应为________。
到三角形三边距离相等的点叫做三角形的
△ABC中其周长为7,AB=3,当BC=________时,△ABC为等腰三角形.
不等式组的解集是______.
如图,直线,点在直线上,点在直线上,,,,则______.
已知,化简得____________.
1 、解答题
先化简,再求值:,其中.
解不等式组
已知:如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°.
求证:AO=BO,CO=DO.
某商场的运动服装专柜,对A,B两种品牌的运动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如下表:
第一次 第二次
A品牌运动服装数/件 20 30
B品牌运动服装数/件 30 40
累计采购款/元 10200 14400
(1)问A,B两种品牌运动服的进货单价各是多少元?
(2)由于B品牌运动服的销量明显好于A品牌,商家决定采购B品牌的件数比A品牌件数的倍多5件,在采购总价不超过21300元的情况下,最多能购进多少件B品牌运动服?
(1)探索:先观察并计算下列各式,在空白处填上“>”、“<”或“=”,并完成后面的问题.
× ,× ,× ,× …
用,,表示上述规律为: ;
(2)利用(1)中的结论,求×的值
(3)设x=,y=试用含x,y的式子表示.
为了尽快实施“脱贫致富奔小康”宏伟意图,某县扶贫工作队为朝阳沟村购买了一批苹果树苗和梨树苗,已知一棵苹果树苗比一棵梨树苗贵2元,购买苹果树苗的费用和购买梨树苗的费用分别是3500元和2500元.
(1)若两种树苗购买的棵数一样多,求梨树苗的单价;
(2)若两种树苗共购买1100棵,且购买两种树苗的总费用不超过6000元,根据(1)中两种树苗的单价,求梨树苗至少购买多少棵.
如图所示,在不等边中,,,的垂直平分线交边于点,交边于点,垂直平分线交边于点,交边于点.
(1)若,求的度数;
(2)若边长为整数,求的周长.
△ABC和△ADE都是等边三角形.
(1)将△ADE绕点A旋转到图①的位置时,连接BD,CE并延长相交于点P(点P与点A重合),有PA+PB=PC(或PA+PC=PB)成立(不需证明),
(2)将△ADE绕点A旋转到图②的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA.PB、PC之间有怎样的数量关系?并加以证明,
(3)将△ADE绕点A旋转到图③的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA.PB、PC之间有怎样的数量关系?直接写出结论,不需要证明.
答案解析
1 、选择题
【考点】最简分式
【分析】最简分式的标准是分子,分母中不含有公因式,不能再约分.判断的方法是把分子、分母分解因式,并且观察有无互为相反数的因式,这样的因式可以通过符号变化化为相同的因式从而进行约分.
解:A. 符合最简分式;
B、不符合最简分式,
C. =不符合最简分式,
D. =不符合最简分式.
故选A.
【点评】此题考查最简分式问题,分式的化简过程,首先要把分子分母分解因式,互为相反数的因式是比较易忽视的问题.在解题中一定要引起注意.
【考点】二次根式有意义的条件.
【分析】根据二次根式有意义的条件即可求出x的值.
解:由题意可知:
解得:x=
故选C
【点评】本题考查二次根式有意义的条件,解题的关键是正确理解二次根式有意义的条件,本题属于基础题型。
【考点】三角形三边关系.
【分析】本题是一个三角形第三边取值范围的题,第三边值在其他两边之和,和两边之差之间.
解:依题意,在三角形AOB中,
OA﹣OB<AB<OA+OB,OA=15米,OB=10米,
即5米<AB<25米.
所以15米符合题意.
故选B.
【点评】本题考查了三角形三边关系,第三边的在范围中选得.
【考点】全等三角形的判定和性质,角平分线的性质
【分析】证明△ABD≌△AED即可得出DE的长.
解:∵DE⊥AC,
∴∠AED=∠B=90°,
∵AD平分∠BAC,
∴∠BAD=∠EAD,
又∵AD=AD,
∴△ABD≌△AED,
∴DE=BE=3,
故选:A.
【点评】本题考查了全等三角形的判定和性质,角平分线的性质,掌握全等三角形的判定定理是解题关键.
【考点】估算无理数的大小
【分析】由正方形的面积等于边长的平方,可得到a2=6,∵4<6<9,∴22<a2<32,即:2<a<3.
解:∵正方形的面积等于边长的平方,
∴a2=6,
∵4<6<9,
∴22<a2<32,
即:2<a<3.
故选:B.
【点评】本题考查了估算无理数的大小,解题的关键是找出和6左右最接近的两个能完全开方的数.
【考点】解一元一次不等式
【分析】去分母、移项,合并同类项,系数化成1即可.
解:>x,
3﹣x>2x,
3>3x,
x<1,
故选:A.
【点评】本题考查了解一元一次不等式,注意:解一元一次不等式的步骤是:去分母、去括号、移项、合并同类项、系数化成1.
【考点】角平分线的性质
【分析】根据角的平分线上的点到角的两边的距离相等即可得.
解:∵BG 是∠ABC 的平分线,DE⊥AB,DF⊥BC,
∴DE=DF=6, 故选:D.
【点评】本题主要考查角平分线的性质,解题的关键是掌握角的平分线上的点到 角的两边的距离相等.
【考点】线段垂直平分线的性质.
【分析】根据线段垂直平分线性质得出AD=DC,AE=CE=4,求出AC=8,AB+BC=15,求出△ABD的周长为AB+BC,代入求出即可.
解:∵AC的垂直平分线分别交AC、BC于E,D两点,
∴AD=DC,AE=CE=4,
即AC=8,
∵△ABC的周长为23,
∴AB+BC+AC=23,
∴AB+BC=23﹣8=15,
∴△ABD的周长为AB+BD+AD=AB+BD+CD=AB+BC=15,
故选B.
【点评】本题考查了线段垂直平分线性质的应用,能熟记线段垂直平分线性质定理的内容是解此题的关键,注意:线段垂直平分线上的点到线段两个端点的距离相等.
【考点】等腰三角形的判定与性质,三角形内角和定理,三角外角的性质
【分析】由在△ABC中,AB=AC,∠A=36°,根据等边对等角,即可求得∠ABC与∠ACB的度数,又由BD、CE分别为∠ABC与∠ACB的角平分线,即可求得∠ABD=∠CBD=∠ACE=∠BCE=∠A=36°,然后利用三角形内角和定理与三角形外角的性质,即可求得∠BEF=∠BFE=∠ABC=∠ACB=∠CDF=∠CFD=72°,由等角对等边,即可求得答案.
解:∵在△ABC中,AB=AC,∠A=36°, ∴∠ABC=∠ACB= =72°,
∵BD、CE分别为∠ABC与∠ACB的角平分线,
∴∠ABD=∠CBD=∠ACE=∠BCE=∠A=36°,
∴AE=CE,AD=BD,BF=CF,
∴△ABC,△ABD,△ACE,△BFC是等腰三角形,
∵∠BEC=180°﹣∠ABC﹣∠BCE=72°,∠CDB=180°﹣∠BCD﹣∠CBD=72°,∠EFB=∠DFC=∠CBD+∠BCE=72°,
∴∠BEF=∠BFE=∠ABC=∠ACB=∠CDF=∠CFD=72°,
∴BE=BO,CF=CD,BC=BD=CF,
∴△BEF,△CDF,△BCD,△CBE是等腰三角形.
∴图中的等腰三角形有8个.
故选B.
【点评】本题考查了等腰三角新的判定与性质、三角形内角和定理以及三角外角的性质.此题难度不大,解题的关键是求得各角的度数,掌握等角对等边与等边对等角定理的应用.
【考点】分式方程的增根
【分析】根据分式方程有增根可求出,方程去分母后将代入求解即可.
解:∵分式方程有增根,
∴,
去分母,得,
将代入,得,
解得.
故选:D.
【点评】本题考查了分式方程的无解问题,掌握分式方程中增根的定义及增根产生的原因是解题的关键.
1 、填空题
【考点】实数的性质
【分析】先化简,再求倒数即可.
解:∵=3,
∴的倒数等于.
【点评】本题考查了算术平方根的意义及倒数的定义,根据算术平方根的定义正确化简是解答本题的关键.
【考点】科学记数法—表示较小的数.
【分析】绝对值小于1的数也可以利用科学记数法表示,一般形式为a×10﹣n,与绝对值大于1数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
解:0.000 000 035=3.5×10﹣8.
故答案是:3.5×10﹣8.
【点评】本题考查用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
【考点】三角形三条边的关系
【分析】根据三角形的三边关系解答即可.
解:∵要与长为4、7的两根木条组成三角形,
∴7-4
【考点】三角形的内心
【分析】根据三角形的内心的定义直接写出答案
解:到三角形三边距离相等的点是三条角平分线的交点,叫做三角形的内心
答案:内心
【点评】本题考查了三角形的内心,熟记定义是关键。
【考点】等腰三角形的判定
【分析】由于等腰三角形的两腰相等,题目给出了周长,根据三角形的条件即可求解.
解:因为△ABC中其周长为7,AB=3,
设AB为腰,BC为底时,则BC=7﹣3﹣3=1,可构成三角形;
设AB为腰,BC为腰时,则BC=3,可构成三角形。
设AB为底,则BC= ,可构成三角形;
故答案为:1或2或3
【点评】此题考查了等腰三角形两腰相等的性质,关键是根据三角形的条件解答.
【考点】解一元一次不等式组
【分析】分别求出两个不等式的解集,再找出两个解集的公共部分即可得答案.
解:
解不等式得:,
解不等式得:,
∴不等式组的解集是,
故答案为:
【点评】本题考查解一元一次不等式组,正确得出两个不等式的解集是解题关键.
【考点】等腰三角形的性质,平行线的性质,三角形内角和定理
【分析】利用等腰三角形的性质得到∠C=∠4=,利用平行线的性质得到∠1=∠3=,再根据三角形内角和定理即可求解.
解:如图,延长CB交于点D,
∵AB=BC,∠C=,
∴∠C=∠4=,
∵,∠1=,
∴∠1=∠3=,
∵∠C +∠3+∠2+∠4 =,即
∴
故答案为:.
【点评】本题考查了等腰三角形的性质,平行线的性质以及三角形内角和定理的应用,解决问题的关键是辅助线的作法,注意运用两直线平行,同位角相等.
【考点】二次根式的性质与化简
【分析】根据完全平方公式结合二次根式的性质进行化简即可求得答案.
解:∵0
∴
=
=
=,
故答案为:.
【点评】本题考查了二次根式的性质与化简,熟练掌握完全平方公式的结构特征是解本题的关键.
1 、解答题
【考点】分式的化简求值
【分析】第一个小括号,先通分再求和,结合平方差公式、完全平方公式将因式分解成,再将分式的除法转化为乘法运算,约分化简,最后代入数值计算即可.
解:
当时,
原式
.
【点评】本题考查分式的化简求值,涉及平方差、完全平方公式等因式分解法,是重要考点,难度较易,掌握相关知识是解题关键.
【考点】解一元一次不等式组
【分析】分别解出每个不等式的解,再得出不等式组的解集.
解: ,
解不等式①得:x>-1,
解不等式②得:x<2,
∴不等式组的解集为:-1
【分析】根据HL证明Rt△ACB≌Rt△ADB,得∠ABC=∠BAD,根据等角对等边,得OA=OB,所以,由AD﹣OA=BC﹣OB,得OD=OC.
证明:∵∠C=∠D=90°,
∴△ACB和△ADB为直角三角形,
在Rt△ACB和Rt△ADB中,
,
∴Rt△ACB≌Rt△ADB,
∴∠ABC=∠BAD,
∴OA=OB,
∵AD=BC,
∴AD﹣OA=BC﹣OB,
即OD=OC.
【点评】本题考核知识点:全等三角形,等腰三角形. 解题关键点:运用全等三角形的性质和等腰三角形性质证明线段相等.
【考点】二元一次方程组的应用,一元一次不等式的应用
【分析】(1)直接利用两次采购的总费用得出等式进而得出答案,
(2)利用采购B品牌的件数比A品牌件数的倍多5件,在采购总价不超过21300元,进而得出不等式求出答案.
解:(1)设A,B两种品牌运动服的进货单价各是x元和y元,根据题意可得:
,
解得:,
答:A,B两种品牌运动服的进货单价各是240元和180元,
(2)设购进A品牌运动服m件,购进B品牌运动服(m+5)件,
则240m+180(m+5)≤21300,
解得:m≤40,
经检验,不等式的解符合题意,
∴m+5≤×40+5=65,
答:最多能购进65件B品牌运动服.
【点评】此题主要考查了一元一次不等式的应用和二元一次方程组的应用,正确得出等量关系是解题关键.
【考点】二次根式的乘除法
【分析】(1)先求出每个式子的值,再比较即可;
(2)根据规律,把被开方数相乘,根指数不变,即可求出答案;
(3)先分解质因数,再根据规律得出,即可得出答案.
解:(1)∵×=2×4=8,==8,
∴×=,
×=,
×=
×=,
故答案为:=,=,=,=, =(a≥0,b≥0);
(2)×
=
=
=2;
(3)∵x=,y=,
∴=
=
=x x y
=x2y.
【点评】本题考查了二次根式的乘除,能根据求出的结果得出规律是解此题的关键.
【考点】分式方程的应用;一元一次不等式的应用.
【分析】(1)设梨树苗的单价为x元,则苹果树苗的单价为(x+2)元,根据两种树苗购买的棵树一样多列出方程求出其解即可;
(2)设购买梨树苗种树苗a棵,苹果树苗则购买棵,根据购买两种树苗的总费用不超过6000元建立不等式求出其解即可.
解:(1)设梨树苗的单价为x元,则苹果树苗的单价为(x+2)元,
依题意得: =,
解得x=5.
经检验x=5是原方程的解,且符合题意.
答:梨树苗的单价是5元;
(2)设购买梨树苗种树苗a棵,苹果树苗则购买棵,
依题意得:(5+2)+5a≤6000,
解得a≥850.
答:梨树苗至少购买850棵.
【点评】本题考查了列分式方程解实际问题的运用,一元一次不等式解实际问题的运用,解答时由方程求出两种树苗的单价是关键.
【考点】线段垂直平分线的性质,三角形三边关系,三角形内角和定理
【分析】(1)根据垂直平分线的性质得到和,再根据三角形内角和去算出角的度数;
(2)根据三角形三边关系求出BC长,再根据垂直平分线的性质证明的周长等于BC的长.
解:(1)∵DE、MN分别是线段AB和线段AC的垂直平分线,
∴AE=BE,AN=CN,
∴,,
∵,
∴,
∴;
(2)在中,,即,
∵BC边长是整数,
∴BC的长度可以取2、3、4,
∵是不等边的,
∴BC=4,
由(1)知AE=BE,AN=CN,
∴.
【点评】本题考查垂直平分线的性质,三角形三边关系和内角和,解题的关键是掌握垂直平分线的性质.
【考点】全等三角形的判定与性质,等边三角形的判定与性质.
【分析】(2)证明△ABD≌△ACE(SAS)和△BAF≌△CAP(SAS),得AF=AP,∠BAF=∠CAP,再证明△AFP是等边三角形,最后由线段的和可得结论,
(3)如图③,在PC上截取CM=PB,连接AM,同理可得结论.
解:(2)PB=PA+PC,理由如下:
如图②,在BP上截取BF=PC,连接AF,
∵△ABC、△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAC+∠CAD=∠CAD+∠DAE,
即∠DAB=∠EAC,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∵AB=AC,BF=CP,
∴△BAF≌△CAP(SAS),
∴AF=AP,∠BAF=∠CAP,
∴∠BAC=∠PAF=90°,
∴△AFP是等边三角形,
∴PF=PA,
∴PB=BF+PF=PC+PA,
(3)PC=PA+PB,理由如下:
如图③,在PC上截取CM=PB,连接AM,
同理得:△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∵AB=AC,PB=CM,
∴△AMC≌△APB(SAS),
∴AM=AP,∠BAP=∠CAM,
∴∠BAC=∠PAM=60°,
∴△AMP是等边三角形,
∴PM=PA,
∴PC=PM+CM=PA+PB.
【点评】本题考查了等边三角形的性质、全等三角形的判定与性质等知识,熟练掌握等边三角形的性质,证明△ABD≌△ACE是解题的关键,属于中考常考题型.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
