1.6 利用三角函数测高 课件(共36张PPT)
文档属性
| 名称 | 1.6 利用三角函数测高 课件(共36张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-20 18:04:43 | ||
图片预览




文档简介
(共36张PPT)
1.6利用三角函数测高
北师大版 九年级 下册
教学目标
教学目标:1、掌握坡度、坡比的概念,并灵活运用坡度、坡比的概念求
出物体的高度;
2、能够设计活动方案、自制测倾器和运用测倾器进行实地测
量以及撰写活动报告的过程;
3、能够综合运用直角三角形边角关系的知识解决实际问题.
教学重点:利用已测量的数据综合运用直角三角形边角关系解决实际问题
教学难点:能够综合运用直角三角形边角关系的知识解决实际问题.
问题1:在现实生活中需要测量像旗杆、高楼、塔等较高且顶部不可到达的物体的高度,根据我们所学的知识,同学们有哪些测量方案
问题2:这些测量的方法都用到了什么知识?
问题3:如何利用直角三角形的边角关系,测量底部不可以直接 到达的物体的高度呢?
今天让我们一起去探究学习如何利用三角函数测高, 学完本节内容相信大家就能轻松解决上面的问题了.
0
30
30
60
60
90
90
P
Q
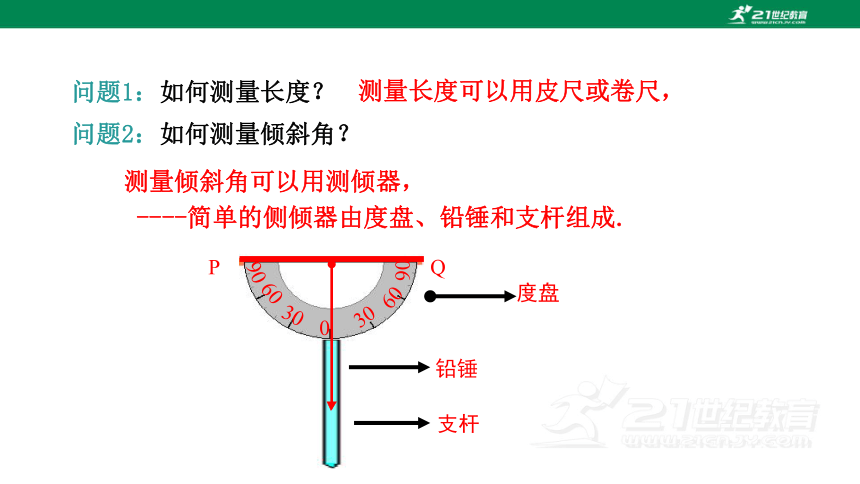
度盘
铅锤
支杆
问题2:如何测量倾斜角?
测量倾斜角可以用测倾器,
----简单的侧倾器由度盘、铅锤和支杆组成.
问题1:如何测量长度?
测量长度可以用皮尺或卷尺,
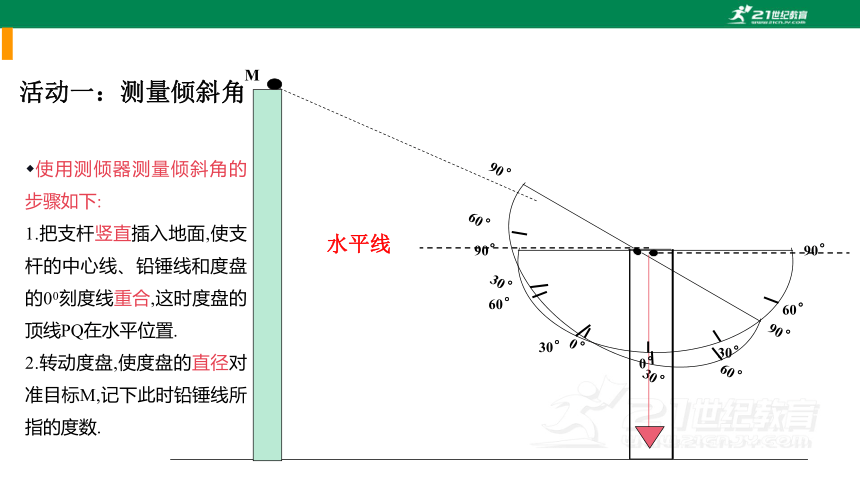
活动一:测量倾斜角
30°
0°
60°
90°
90°
60°
30°
30°
0°
60°
90°
90°
60°
30°
水平线
使用测倾器测量倾斜角的步骤如下:
1.把支杆竖直插入地面,使支杆的中心线、铅锤线和度盘的00刻度线重合,这时度盘的顶线PQ在水平位置.
2.转动度盘,使度盘的直径对准目标M,记下此时铅锤线所指的度数.
M
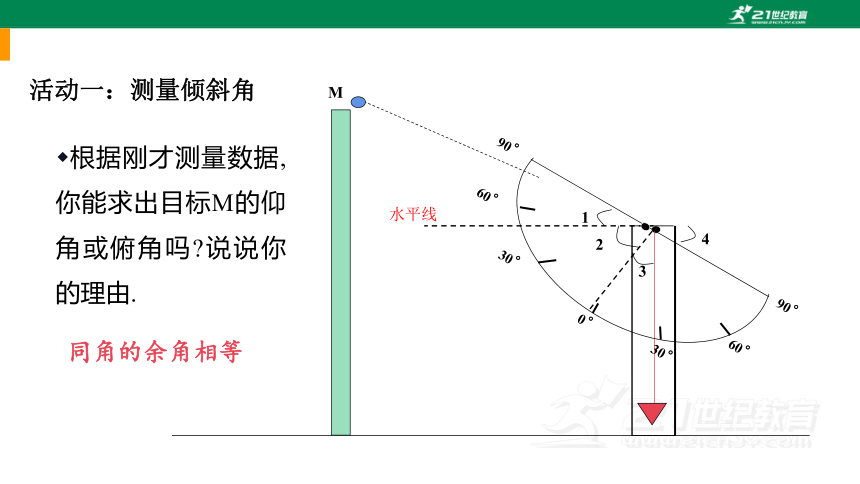
活动一:测量倾斜角
根据刚才测量数据,你能求出目标M的仰角或俯角吗 说说你的理由.
1
2
3
4
30°
0°
60°
90°
90°
60°
30°
水平线
M
同角的余角相等
新知讲解
合作学习
活动二:测量底部可以到达的物体的高度.
所谓“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体的底部之间的距离.
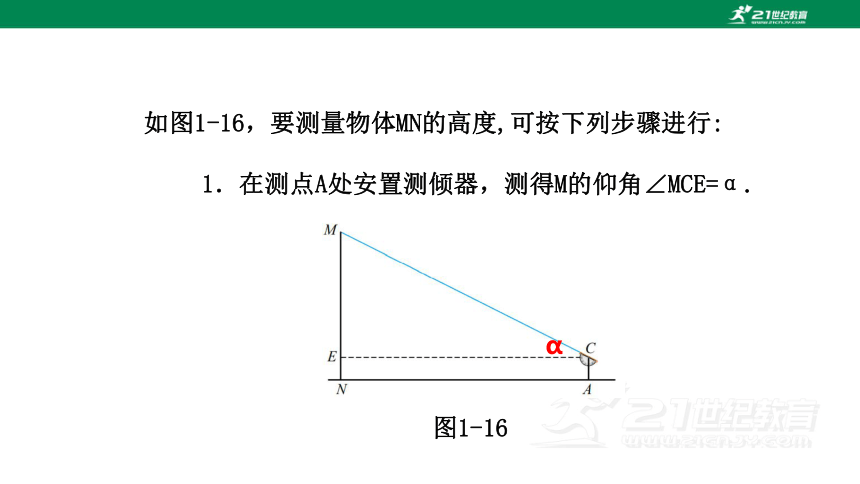
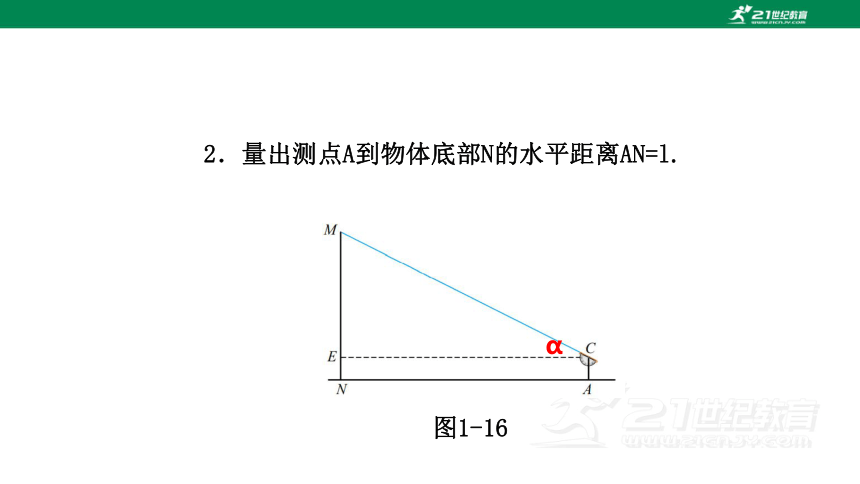
图1-16
α
如图1-16,要测量物体MN的高度,可按下列步骤进行:
1.在测点A处安置测倾器,测得M的仰角∠MCE=α.
图1-16
α
2.量出测点A到物体底部N的水平距离AN=l.
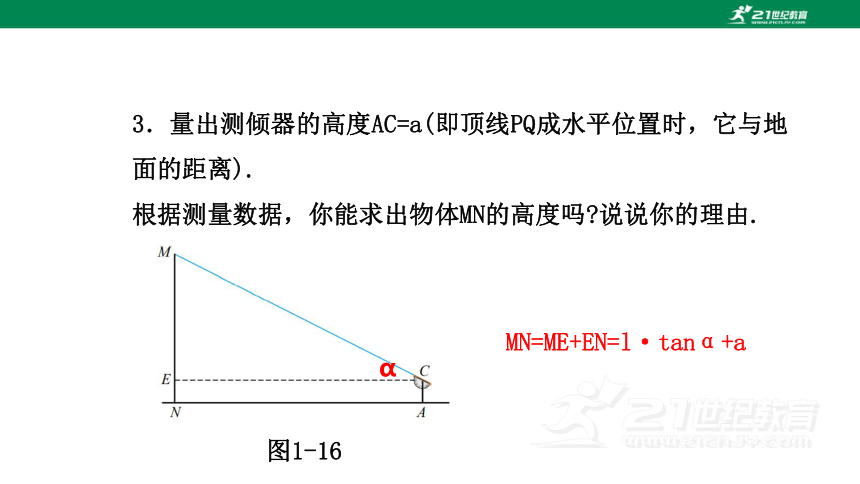
3.量出测倾器的高度AC=a(即顶线PQ成水平位置时,它与地面的距离).
根据测量数据,你能求出物体MN的高度吗 说说你的理由.
MN=ME+EN=l·tanα+a
α
图1-16
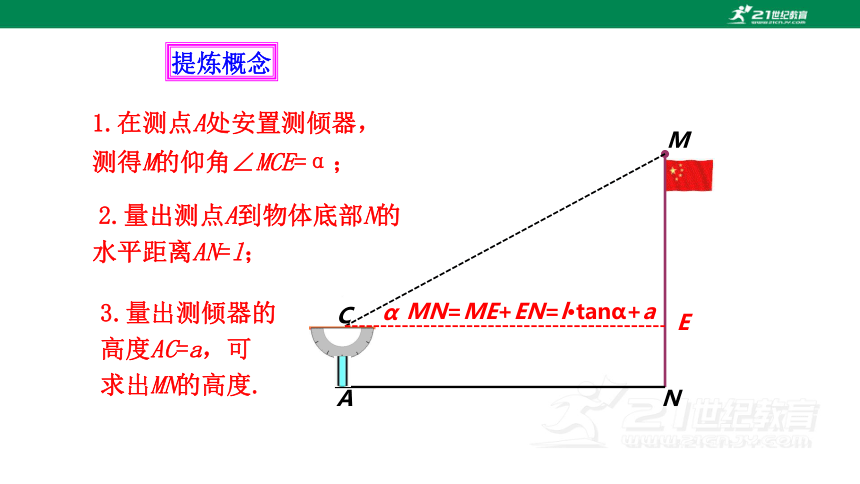
提炼概念
A
C
M
N
E
α
1.在测点A处安置测倾器,测得M的仰角∠MCE=α;
2.量出测点A到物体底部N的水平距离AN=l;
3.量出测倾器的高度AC=a,可求出MN的高度.
MN=ME+EN=l·tanα+a
典例精讲
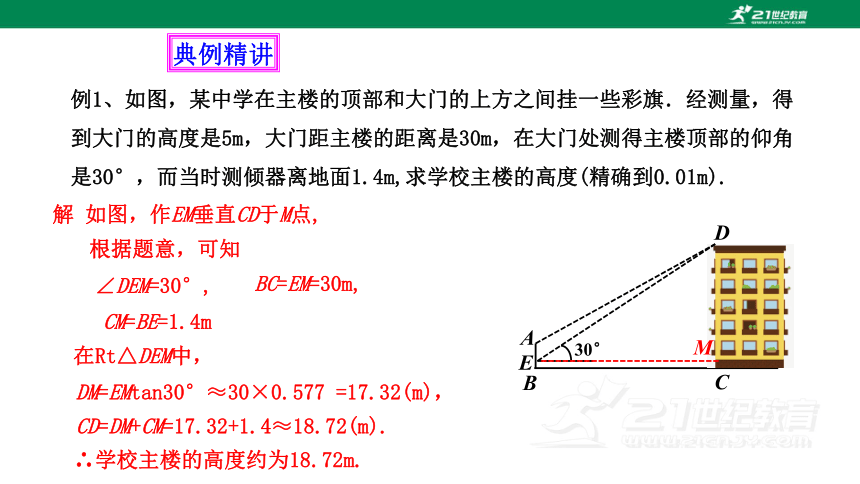
例1、如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗.经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30°,而当时测倾器离地面1.4m,求学校主楼的高度(精确到0.01m).
C
A
B
E
D
30°
M
解 如图,作EM垂直CD于M点,
∠DEM=30°,
根据题意,可知
CM=BE=1.4m
BC=EM=30m,
在Rt△DEM中,
DM=EMtan30°≈30×0.577 =17.32(m),
CD=DM+CM=17.32+1.4≈18.72(m).
∴学校主楼的高度约为18.72m.
总结:与仰角(或俯角)有关的计算问题的解决方法:
首先弄清哪个角是仰角(或俯角),再选择或构造恰当的直角三角形,将仰角或俯角置于这个三角形中,选择正确的三角函数,并借助计算器求出要求的量.
活动三:测量底部不可以到达的物体的高度.
所谓“底部不可以到达”,就是在地面上不能直接测得测点与被测物体的底部之间的距离.
如图1-17,要测量物体MN的高度,可按下列步骤进行:
图1-17
1.在测点A处安置测倾器,测得此时M的仰角∠MCE=α.
2.在测点A与物体之间的B处安置测倾器(A,B与N在一条直线上,且A,B之间的距离可以直接测得),测得此时M的仰角∠MDE=β.
图1-17
α
β
(1)测倾器的使用
(2)误差的解决办法---用平均值
(3)到目前为止,你有哪些测量物体高度的方法?
A
C
M
E
N
A
C
M
E
N
D
B
3.量出测倾器的高度AC=BD=a ,以及测点A,B之间的距离AB=b.
根据测量数据,你能求出物体MN的高度吗 说说你的理由.
α
β
b
a
(1)到目前为止,你有哪些测量物体高度的方法
议一议
一、测量底部可以到达的物体的高度,如图
A
C
M
E
N
二、测量底部不可以直接到达的物体的高度,如图
A
C
M
E
N
D
B
(2)如果一个物体的高度已知或容易测量,那么如何测量某测点到该物体的水平距离
N
M
A
α
归纳概念
总结:从同一点看不同的位置,有两个视角,不同位置之间有距离,作垂线将两个视角都放在直角三角形中,利用不同位置之间的距离列方程来解决问题.
课堂练习
1.如图,窗子高AB=m米,窗子外面上方0.2米的点C处安装水平遮阳板CD=1米,当太阳光线与水平线成α=60°角时,光线刚好不能直接射人室内,则m的值是( )
A.m=+0.8 B.m=+0.2
C.m=-0.2 D.m=-0.8
C
2.如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为( )
A.
B.30sin α米
C.30tan α米
D.30cos α米
C
3.如图,航模小组用无人机来测量建筑物BC的高度,无人机从A处测得建筑物顶部B的仰角为45°,测得底部C的俯角为60°,若此时无人机与该建筑物的水平距离AD为30m,则该建筑物的高度BC为_____m.(结果保留根号)
【答案】(30+30).
【分析】在Rt△ABD中,根据正切函数求得BD=AD tan∠BAD,在
Rt△ACD中,求得CD=AD tan∠CAD,再根据BC=BD+CD,
代入数据计算即可.
【详解】解:∵在Rt△ABD中,AD=90,∠BAD=45°,
∴BD=AD=30(m),
∵在Rt△ACD中,∠CAD=60°,
∴CD=AD tan60°=30×=30(m),
∴BC=BD+CD=30+30(m)
答:该建筑物的高度BC约为(30+30)米.
故答案为:(30+30).
4.如图,小丽的房间内有一张长200m,高50cm的床靠墙摆放,在上方安装空调,空调下沿与EF墙垂直,出风口F离墙20cm,空调开启后,挡风板FG与EF夹角成136°,风沿FG方向吹出,为了让空调风不直接吹到床上,空调安装的高度(BC的长)至少为多少?(精确到个位)(参考数据:cos46°≈0.69,tan46°≈1.04,sin46°≈0.72)
【分析】连接AF,作FH⊥AD构造直角三角形运用三角函数解出FH,再将床高加上即可求出EC的值.
【详解】当A、F在一条直线时,就正好不会吹到床上,连接AF,过点F作FH⊥AD,
∵AD=200,HD=20,
∴AH=180,
∵∠EFA=136°,
∴∠FAD=46°,
∴FH=AH·tan46°=180×1.04=187.2
∴ED=FH=187.2,
∴EC=187.2+50=237.2≈237.
故答案为237.
5. 如图,某班学生利用周末到白塔山去参观“晏阳初博物馆”.下面是两位同学的一段对话:
甲:我站在N处看塔顶,仰角为60°.
乙:我站在M处看塔顶,仰角为30°.
甲:我们的身高都是1.5 m.
乙:我们和塔在一条直线上,且我们相距20 m.请你根据两位同学的对话,计算白塔的高度.(结果精确到1 m).
由题意知∠CAB=30°,∠CBD=60°,AB=20 m,
AM=BN=DP=1.5 m.
在△ABC中,∠CBD=∠ACB+∠CAB,
∴∠ACB=60°-30°=30°.
∴∠ACB=∠CAB.∴BC=AB=20 m.
在Rt△CBD中,BC=20 m,∠CBD=60°,sin ∠CBD=
∴CD=BC·sin ∠CBD=20sin 60°=20× (m).
∴CP=CD+DP=10 +1.5≈19(m).
答:白塔的高度约为19 m.
解:
6.数学课外学习小组利用矩形建筑物ABED测量广场灯塔CF的高,如图所示,在点B处测得灯塔顶端C的仰角为28°,在点D处测得灯塔顶端C的仰角为45°,已知AB=10m,AD=30m.求灯塔CF的高(结果保留整数).
(参考数据:tan28°≈0.53, cos28°≈0.88,sin28°≈0.47,≈1.41)
【详解】解:延长BE交CD于点G,交CF于点H,
在Rt△DEG中,∠EDG=45°,
∴EG=DE=10m.∠EGD=45°
设CH=xm,
在Rt△CGH中,∠CGH=∠EGD=45°,
∴GH=xm
在Rt△CBH中,∠CBH=28°,
∴tan∠CBH=,
即:=tan28°
解这个方程得:x≈45.1,
经检验:x≈45.1符合题意.
∴灯塔的高CF=55.1≈55(m)
答:灯塔的高为55米.
课堂总结
利用三角函数测高
测倾器的认识及使用
测量底部可以到达的物体的高度(一次测量仰角)
测量底部不可以到达的物体的高度(两次测量仰角)
利用解三角形的知识,求出物体的高度
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.6利用三角函数测高
北师大版 九年级 下册
教学目标
教学目标:1、掌握坡度、坡比的概念,并灵活运用坡度、坡比的概念求
出物体的高度;
2、能够设计活动方案、自制测倾器和运用测倾器进行实地测
量以及撰写活动报告的过程;
3、能够综合运用直角三角形边角关系的知识解决实际问题.
教学重点:利用已测量的数据综合运用直角三角形边角关系解决实际问题
教学难点:能够综合运用直角三角形边角关系的知识解决实际问题.
问题1:在现实生活中需要测量像旗杆、高楼、塔等较高且顶部不可到达的物体的高度,根据我们所学的知识,同学们有哪些测量方案
问题2:这些测量的方法都用到了什么知识?
问题3:如何利用直角三角形的边角关系,测量底部不可以直接 到达的物体的高度呢?
今天让我们一起去探究学习如何利用三角函数测高, 学完本节内容相信大家就能轻松解决上面的问题了.
0
30
30
60
60
90
90
P
Q
度盘
铅锤
支杆
问题2:如何测量倾斜角?
测量倾斜角可以用测倾器,
----简单的侧倾器由度盘、铅锤和支杆组成.
问题1:如何测量长度?
测量长度可以用皮尺或卷尺,
活动一:测量倾斜角
30°
0°
60°
90°
90°
60°
30°
30°
0°
60°
90°
90°
60°
30°
水平线
使用测倾器测量倾斜角的步骤如下:
1.把支杆竖直插入地面,使支杆的中心线、铅锤线和度盘的00刻度线重合,这时度盘的顶线PQ在水平位置.
2.转动度盘,使度盘的直径对准目标M,记下此时铅锤线所指的度数.
M
活动一:测量倾斜角
根据刚才测量数据,你能求出目标M的仰角或俯角吗 说说你的理由.
1
2
3
4
30°
0°
60°
90°
90°
60°
30°
水平线
M
同角的余角相等
新知讲解
合作学习
活动二:测量底部可以到达的物体的高度.
所谓“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体的底部之间的距离.
图1-16
α
如图1-16,要测量物体MN的高度,可按下列步骤进行:
1.在测点A处安置测倾器,测得M的仰角∠MCE=α.
图1-16
α
2.量出测点A到物体底部N的水平距离AN=l.
3.量出测倾器的高度AC=a(即顶线PQ成水平位置时,它与地面的距离).
根据测量数据,你能求出物体MN的高度吗 说说你的理由.
MN=ME+EN=l·tanα+a
α
图1-16
提炼概念
A
C
M
N
E
α
1.在测点A处安置测倾器,测得M的仰角∠MCE=α;
2.量出测点A到物体底部N的水平距离AN=l;
3.量出测倾器的高度AC=a,可求出MN的高度.
MN=ME+EN=l·tanα+a
典例精讲
例1、如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗.经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30°,而当时测倾器离地面1.4m,求学校主楼的高度(精确到0.01m).
C
A
B
E
D
30°
M
解 如图,作EM垂直CD于M点,
∠DEM=30°,
根据题意,可知
CM=BE=1.4m
BC=EM=30m,
在Rt△DEM中,
DM=EMtan30°≈30×0.577 =17.32(m),
CD=DM+CM=17.32+1.4≈18.72(m).
∴学校主楼的高度约为18.72m.
总结:与仰角(或俯角)有关的计算问题的解决方法:
首先弄清哪个角是仰角(或俯角),再选择或构造恰当的直角三角形,将仰角或俯角置于这个三角形中,选择正确的三角函数,并借助计算器求出要求的量.
活动三:测量底部不可以到达的物体的高度.
所谓“底部不可以到达”,就是在地面上不能直接测得测点与被测物体的底部之间的距离.
如图1-17,要测量物体MN的高度,可按下列步骤进行:
图1-17
1.在测点A处安置测倾器,测得此时M的仰角∠MCE=α.
2.在测点A与物体之间的B处安置测倾器(A,B与N在一条直线上,且A,B之间的距离可以直接测得),测得此时M的仰角∠MDE=β.
图1-17
α
β
(1)测倾器的使用
(2)误差的解决办法---用平均值
(3)到目前为止,你有哪些测量物体高度的方法?
A
C
M
E
N
A
C
M
E
N
D
B
3.量出测倾器的高度AC=BD=a ,以及测点A,B之间的距离AB=b.
根据测量数据,你能求出物体MN的高度吗 说说你的理由.
α
β
b
a
(1)到目前为止,你有哪些测量物体高度的方法
议一议
一、测量底部可以到达的物体的高度,如图
A
C
M
E
N
二、测量底部不可以直接到达的物体的高度,如图
A
C
M
E
N
D
B
(2)如果一个物体的高度已知或容易测量,那么如何测量某测点到该物体的水平距离
N
M
A
α
归纳概念
总结:从同一点看不同的位置,有两个视角,不同位置之间有距离,作垂线将两个视角都放在直角三角形中,利用不同位置之间的距离列方程来解决问题.
课堂练习
1.如图,窗子高AB=m米,窗子外面上方0.2米的点C处安装水平遮阳板CD=1米,当太阳光线与水平线成α=60°角时,光线刚好不能直接射人室内,则m的值是( )
A.m=+0.8 B.m=+0.2
C.m=-0.2 D.m=-0.8
C
2.如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为( )
A.
B.30sin α米
C.30tan α米
D.30cos α米
C
3.如图,航模小组用无人机来测量建筑物BC的高度,无人机从A处测得建筑物顶部B的仰角为45°,测得底部C的俯角为60°,若此时无人机与该建筑物的水平距离AD为30m,则该建筑物的高度BC为_____m.(结果保留根号)
【答案】(30+30).
【分析】在Rt△ABD中,根据正切函数求得BD=AD tan∠BAD,在
Rt△ACD中,求得CD=AD tan∠CAD,再根据BC=BD+CD,
代入数据计算即可.
【详解】解:∵在Rt△ABD中,AD=90,∠BAD=45°,
∴BD=AD=30(m),
∵在Rt△ACD中,∠CAD=60°,
∴CD=AD tan60°=30×=30(m),
∴BC=BD+CD=30+30(m)
答:该建筑物的高度BC约为(30+30)米.
故答案为:(30+30).
4.如图,小丽的房间内有一张长200m,高50cm的床靠墙摆放,在上方安装空调,空调下沿与EF墙垂直,出风口F离墙20cm,空调开启后,挡风板FG与EF夹角成136°,风沿FG方向吹出,为了让空调风不直接吹到床上,空调安装的高度(BC的长)至少为多少?(精确到个位)(参考数据:cos46°≈0.69,tan46°≈1.04,sin46°≈0.72)
【分析】连接AF,作FH⊥AD构造直角三角形运用三角函数解出FH,再将床高加上即可求出EC的值.
【详解】当A、F在一条直线时,就正好不会吹到床上,连接AF,过点F作FH⊥AD,
∵AD=200,HD=20,
∴AH=180,
∵∠EFA=136°,
∴∠FAD=46°,
∴FH=AH·tan46°=180×1.04=187.2
∴ED=FH=187.2,
∴EC=187.2+50=237.2≈237.
故答案为237.
5. 如图,某班学生利用周末到白塔山去参观“晏阳初博物馆”.下面是两位同学的一段对话:
甲:我站在N处看塔顶,仰角为60°.
乙:我站在M处看塔顶,仰角为30°.
甲:我们的身高都是1.5 m.
乙:我们和塔在一条直线上,且我们相距20 m.请你根据两位同学的对话,计算白塔的高度.(结果精确到1 m).
由题意知∠CAB=30°,∠CBD=60°,AB=20 m,
AM=BN=DP=1.5 m.
在△ABC中,∠CBD=∠ACB+∠CAB,
∴∠ACB=60°-30°=30°.
∴∠ACB=∠CAB.∴BC=AB=20 m.
在Rt△CBD中,BC=20 m,∠CBD=60°,sin ∠CBD=
∴CD=BC·sin ∠CBD=20sin 60°=20× (m).
∴CP=CD+DP=10 +1.5≈19(m).
答:白塔的高度约为19 m.
解:
6.数学课外学习小组利用矩形建筑物ABED测量广场灯塔CF的高,如图所示,在点B处测得灯塔顶端C的仰角为28°,在点D处测得灯塔顶端C的仰角为45°,已知AB=10m,AD=30m.求灯塔CF的高(结果保留整数).
(参考数据:tan28°≈0.53, cos28°≈0.88,sin28°≈0.47,≈1.41)
【详解】解:延长BE交CD于点G,交CF于点H,
在Rt△DEG中,∠EDG=45°,
∴EG=DE=10m.∠EGD=45°
设CH=xm,
在Rt△CGH中,∠CGH=∠EGD=45°,
∴GH=xm
在Rt△CBH中,∠CBH=28°,
∴tan∠CBH=,
即:=tan28°
解这个方程得:x≈45.1,
经检验:x≈45.1符合题意.
∴灯塔的高CF=55.1≈55(m)
答:灯塔的高为55米.
课堂总结
利用三角函数测高
测倾器的认识及使用
测量底部可以到达的物体的高度(一次测量仰角)
测量底部不可以到达的物体的高度(两次测量仰角)
利用解三角形的知识,求出物体的高度
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
