2022-2023学年高二上学期物理人教版(2019)选择性必修第一册1.5.1 弹性碰撞和非弹性碰撞 课件(共39张PPT)
文档属性
| 名称 | 2022-2023学年高二上学期物理人教版(2019)选择性必修第一册1.5.1 弹性碰撞和非弹性碰撞 课件(共39张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 15.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-12-20 18:56:33 | ||
图片预览








文档简介
(共39张PPT)
第一章 动量守恒定律
1.5.1 弹性碰撞和非弹性碰撞
碰撞是自然界常见的现象。碰撞瞬间系统动量守恒,碰撞还有什么特点?
高速飞行的陨石撞击地球,对地表产生极大的破坏;
这节课我们将从形变的角度来看碰撞系统动能特点
新课引入
网球受球拍撞击后反弹后,形状完全保持不变。
掘进机撞击地面,地面钻出一个大窟窿······
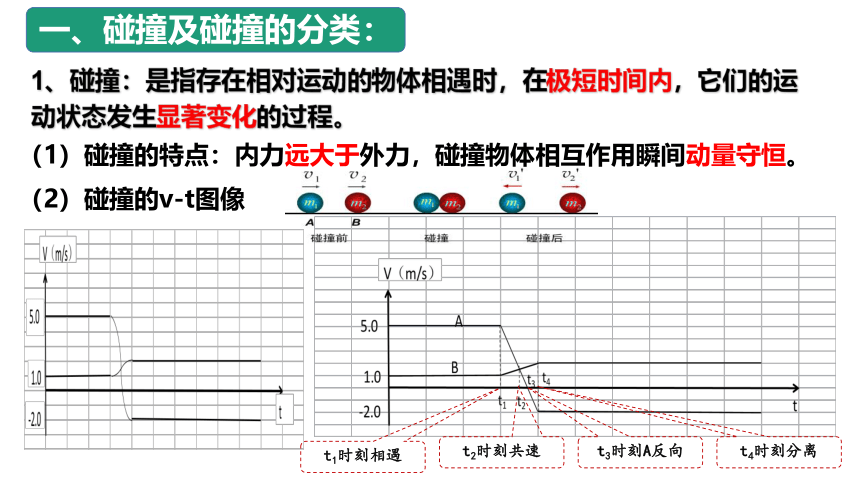
1、碰撞:是指存在相对运动的物体相遇时,在极短时间内,它们的运动状态发生显著变化的过程。
一、碰撞及碰撞的分类:
(2)碰撞的v-t图像
t1时刻相遇
t2时刻共速
t3时刻A反向
t4时刻分离
(1)碰撞的特点:内力远大于外力,碰撞物体相互作用瞬间动量守恒。
碰撞之前 碰撞之后
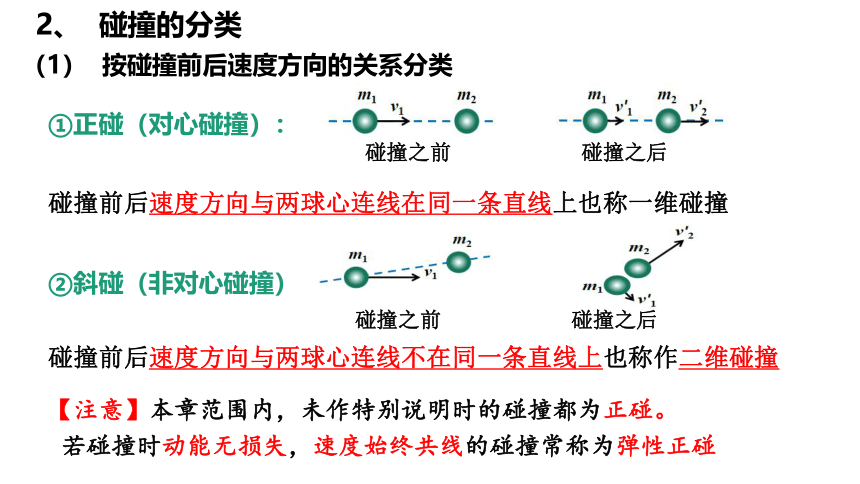
①正碰(对心碰撞):
②斜碰(非对心碰撞)
碰撞前后速度方向与两球心连线在同一条直线上也称一维碰撞
碰撞前后速度方向与两球心连线不在同一条直线上也称作二维碰撞
碰撞之前 碰撞之后
(1) 按碰撞前后速度方向的关系分类
【注意】本章范围内,未作特别说明时的碰撞都为正碰。
若碰撞时动能无损失,速度始终共线的碰撞常称为弹性正碰
2、 碰撞的分类
碰撞的形变恢复情况模拟视频1
碰撞的形变恢复情况模拟视频2
碰撞的形变恢复情况模拟视频3
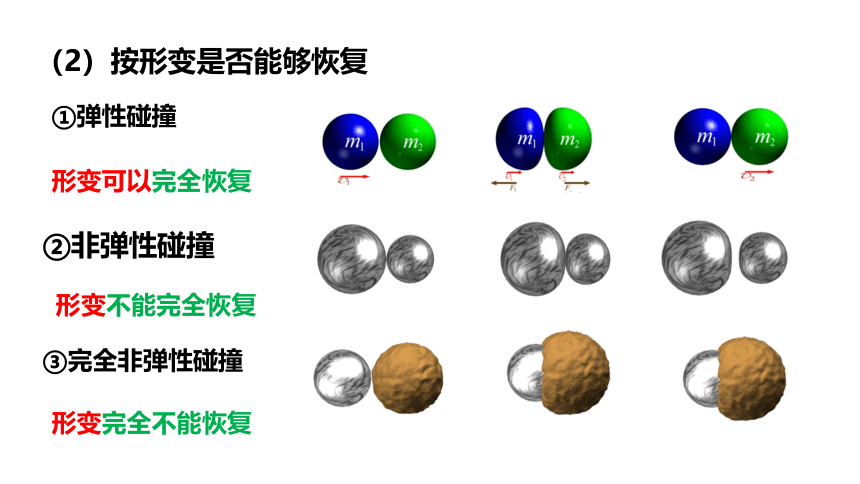
①弹性碰撞
②非弹性碰撞
③完全非弹性碰撞
(2)按形变是否能够恢复
形变可以完全恢复
形变不能完全恢复
形变完全不能恢复
(1)系统动能不变原因:
①形变能完全恢复,位移相同X=X'
②外力忽略不计,内力对系统不做功WF+WF'=-F·X+F'·X'=ΔEK系统=0
系统动能不变.
m1
m2
v'1
v'2
X=X'
F=F'
v1
m1
m2
v2
x
F'
F
x'
二、弹性碰撞
1.弹性碰撞定义:形变量能完全恢复,碰撞前后系统总动能几乎不变的碰撞
(2)弹性碰撞的v-t图像:
m1=m2
(3)弹性碰撞的生活实例:
铁球之间、玻璃球之间以较小速度碰撞时,可视为弹性碰撞
动量守恒
动能守恒
解得2
v‘1 如何?1、2、1;2、2、2; v‘2 如何?角标互换;1换2,2换1
若m1=m2,v‘1 =v2 ; v‘2 =v1 m1和m2交换速度。
(4)弹性碰撞一般规律:
解得1
运动物体和静止物体发生弹性正碰的特点
【注意】m1碰撞静止的m2时,无论m1、m2大小关系如何总有:v1<v0 ;
碰后两球速度交换,且v1=0 ,v2=v0
①若m1=m2
②若m1>m2m2
④若m1<m2
碰后两球同向运动运动,且v1<v0<v2
碰后两球反向运动运动,且v2<v1<v0
(5)弹性碰撞特殊规律:(运动碰静止)
③若m1>>m2
碰后两球同向运动运动,且v1≈v0<v2=2v0
⑤若m1<<m2
碰后两球反向运动运动,且v2≈0<v1≈v0
解得
m2
m1
v'1
v'2
(1)动能减少原因:
①形变不能完全恢复,位移不相同X>X'
②外力忽略,系统内力做负功
WF+WF'=-F·X+F'·X'=-F·ΔX=ΔEK系统<0, 系统动能减少.
(3)非弹性碰撞规律:
x'
F
F'
X>X'
F=F'
v1
m1
m2
v2
x
Δx
1、定义:形变量不能完全恢复,碰撞前后系统总动能有明显减少的碰撞
(2)非弹性碰撞的v-t图像:
②动能减少
①动量守恒
m1=m2
三、非弹性碰撞
木球间碰撞,可视为非弹性碰撞
m2
m1
(1)动能损失最多原因:
①形变完全不能恢复,相对位移ΔX最大
②外力可忽略,内力做负功最多
WF+WF'=-F·X+F'·X'=-F·ΔX=ΔEK系统<0系统动能损失最大.
x'
v
ΔX=X-X'最大
F=F'
v1
m1
m2
v2
x
Δx
F'
F
1、定义:形变量完全不能恢复,碰撞前后系统总动能损失最多的碰撞
(2)完全非弹性碰撞的v-t图像:
m1=m2
四、完全非弹性碰撞
(3)完全非弹性碰撞的生活实例:
子弹击打木块时,形变量完全不能恢复,可视为完全非弹性碰撞
若v2=0,则
若v2=0且m+M=nm
当n→∞时,
v共=0;
Ek=0 ;
ΔEk=Ek0
(3)完全非弹性碰撞的一般规律
(4)完全非弹性碰撞的特殊规律
①
②
③
3、碰撞三原则
(1)动量守恒
(2)动能不增加:
(3)速度要合理:
①碰前同向运动,碰前:v后>v前,若碰后未反向,碰后:v后≤v后
②碰前相向运动,碰后至少一个物体方向改变。
三种碰撞规律总结
【例题1】两球A、B在光滑水平面上沿同一直线、同一方向运动, mA=1 kg, mB=2 kg, vA=6 m/s, vB=2 m/s。当A追上B并发生碰撞后,两球A、B速度的可能值是( )。
A.vA'=5 m/s,vB'=2.5 m/s B.vA'=2 m/s,vB'=4 m/s
C.vA'=-4 m/s,vB'=7 m/s D.vA'= 3m/s,vB'=3.5 m/s
BD
五、碰撞规律定性判断
题型1、速度可能性判断
【变式训练】质量为m速度为v的A球,跟质量为3m的静止B球发生正碰,碰撞可能是弹性,也可能非弹性,碰后B球的速度可能为( )
A 0.6v B 0.4v C 0.2v D0.1v
B
三原则使用优先顺序:
①先动量守恒和速度合理,
②后动能不增加,先简单运算后复杂运算
【变式训练】如图所示,光滑水平面上有大小相同的A、B两球在同一直线上运动.两球质量关系为mB=2mA,规定向右为正方向,A、B两球的动量大小均为6 kg·m/s,运动中两球发生碰撞,碰撞后A球的动量增量为-4 kg·m/s,则( )
A
A.左方是A球,碰撞后A、B两球速度大小之比为2∶5B.左方是A球,碰撞后A、B两球速度大小之比为1∶10C.右方是A球,碰撞后A、B两球速度大小之比为2∶5D.右方是A球,碰撞后A、B两球速度大小之比为1∶10
【例题3】(多选) 质量相等的A、B两球在光滑水平桌面上沿同一直线、同一方向运动,A球的动量是7kg·m/s,B球的动量是5kg·m/s,A 球追上B球发生碰撞,碰撞后两球的动量可能值是( )
A.P'A=6 kg·m/s , p'B=6 kg·m/s B.P'A=3 kg·m/s , p'B=9kg·m/s
C.P'A=5kg·m/s , p'B=7kg·m/s D.P'A=-2kg·m/s , p'B=10kg·m/s
AC
题型2、动量可能性判断
【变式训练】光滑水平面上,动能为E0 ,动量大小为p0 的小钢球1与静止的小钢球2发生弹性碰撞,碰后球1的运动反向,碰后球1的动能和动量大小分别记为 E1、p1,球2的动能和动量大小分别记为E2、p2,则必有 ( )
A. E1 < E0 B. p1 < p0
C. E2 > E0 D. p2 > p0
ABD
v0
1
2
3.解释碰撞球现象
【现象解释】
排列碰撞处理方法:碰撞按相互接触的顺序“一对一”依次发生.
相互作用力有明显大小之分,间接接触的作用力较小可忽略,
不能简单处理为“一对多”和“多对多”,除非粘贴在一起。
→v0
1
2
3
4
5
→v0
1
2
3
4
5
→v0
1
2
3
4
5
【1】
→v0
1
2
3
4
5
【2】
→v0
1
2
3
4
5
→v0
1
2
3
4
5
→v0
1
2
3
4
5
【3】
→v0
1
2
3
4
5
【4】
【例题1】(多选)如图甲所示,在光滑水平面上的两小球发生正碰。小球的质量分别为m1和m2。图乙为它们碰撞前后的s-t(位移一时间)图象。已知 m1=0.1 kg。由此可以判断( )
A. 碰前 m2 静止,m1 向右运动
B. 碰后 m2 和 m1 都向右运动
C. m2 = 0.3 kg
D. 碰撞过程中系统损失了 0.4 J 的机械能
AC
六、碰撞规律的定量求值
1.碰撞的图像问题
【例题1】如图所示,一质量为m的子弹以初速度v0水平击中静止于水平地面上的木块并没有击穿,求木块质量分别为2.5m、10m、100m时,子弹和木块因相对运动而产生的内能多大?
2.完全非弹性碰撞规律应用
【例题1】速度为10m/s的塑料球与静止的钢球发生正碰,钢球的质量是塑料球的4倍,碰撞是弹性的,求碰撞后两个小球的速度.
解:由于是弹性碰撞
与塑料球初速度方向相反
与塑料球初速度方向相同
3.特殊弹性碰撞规律应用
【例题2】一 种未知粒子跟静止的氢原子核正碰,测出碰撞后氢原子核的速度3.3×107m/s.该未知粒子跟静止的氮原子核正碰时,测出碰撞后氮原子核的速度是4.4×106m/s.已知氢原子核的质量是mH,氮原子核的质量是14mH,上述碰撞都是弹性碰撞,求未知粒子的质量.
解:设未知粒子质量m,速度v,它与氢和氮原子核碰撞都是弹性碰撞,
解①②两式,得未知粒子的质量为m=mH
①
②
【例题1】如图所示,两质量分别为m和3m的弹性小球叠放在一起,从高度为h处自由下落,且h远大于两球半径,所有碰撞都是弹性碰撞,且都发生在竖直方向,则m质量的小球反弹后能够达到的高度为 ( )
A. h B. 2h
C. 3h D. 4h
m
3m
↓
-
h
D
4.弹性碰撞规律综合应用
m
m
↓
-
h
谢谢 再见!
5 弹性碰撞和非弹性碰撞
知识点一 弹性碰撞和非弹性碰撞
1.(多选)下列关于碰撞的理解正确的是 ( )A.碰撞是指相对运动的物体相遇时,在极短时间内它们的运动状态发生了显著变化的过程B.在碰撞现象中,一般内力都远大于外力,所以可以认为碰撞时系统的动量守恒C.如果碰撞过程中机械能守恒,这样的碰撞叫作非弹性碰撞D.微观粒子的相互作用由于不发生直接接触,所以不能称其为碰撞2.(多选) 动能相同的A、B两球(mA>mB)在光滑的水平面上相向运动,两球相碰后,若其中一球停止运动,则可判定( )A.碰撞前A球的速度小于B球的速度B.碰撞前A球的动量大于B球的动量C.碰撞前后A球的动量变化量大于B球的动量变化量D.碰撞后A球的速度一定为零,B球朝反方向运动
AB
ABD
3.(多选)甲物体在光滑水平面上的运动速度为v1,与静止的乙物体相碰,碰撞过程中无机械能损失.下列结论正确的是( )A.乙的质量等于甲的质量时,碰撞后乙的速度为v1B.乙的质量远远小于甲的质量时,碰撞后乙的速度为2v1C.乙的质量远远大于甲的质量时,碰撞后甲的速度为-v1D.碰撞过程中甲对乙做的功大于乙的动能增量
4.一中子(质量数为1)与一质量数为A(A>1)的原子核发生弹性正碰.若碰前原子核静止,则碰撞前与碰撞后中子的速率之比为( )
ABC
A
5.如图所示,细线上端固定于O点上,其下端系一小球,静止时细线长为L.现将细线和小球拉至图中实线位置, 此时细线与竖直方向的夹角为θ=60°,并在小球原来所在的最低点放置一质量相同的泥球,然后使悬挂的小球从实线位置由静止释放,它运动到最低点时与泥球碰撞并合为一体,它们一起摆动中可达到的最大高度是( )
A.L/2 B.L/4 C.L/8 D.L/16
知识点二 碰撞的可行性6.(多选)质量相等的A、B两球在光滑水平面上沿同一直线向同一方向运动,A球的动量是7 kg·m/s,B球的动量是5 kg·m/s,A球追上B球发生碰撞,则碰撞后A、B两球的动量可能为( )A.p'A=8 kg·m/s,p'B=4 kg·m/sB.p'A=6 kg·m/s,p'B=6 kg·m/sC.p'A=5 kg·m/s,p'B=7 kg·m/sD.p'A=-2 kg·m/s,p'B=14 kg·m/s
C
BC
7.(多选)光滑的水平面上有A、B两个小球,其中A球的动量为10kg·m/s,
B球的动量为12 kg·m/s,A球追上B球并相碰,碰撞后,A球动量变为8 kg·m/s,方向没变,则A、B两球质量之比可能为( )
A.0.5 B.0.6 C.0.65 D.0.75
8.(多选)如图所示,一沙袋用无弹性轻细绳悬于O点.开始时沙袋处于静止状态,一弹丸以水平速度v0击中沙袋后未穿出,二者共同摆动.已知弹丸质量为m,沙袋质量为5m,弹丸和沙袋形状大小忽略不计,弹丸击中沙袋后漏出的沙子质量忽略不计,不计空气阻力,重力加速度为g.下列说法中正确的是( )
A.弹丸打入沙袋前后,细绳所受拉力大小保持不变B.弹丸打入沙袋过程中,弹丸对沙袋的冲量大小
等于沙袋对弹丸的冲量大小
C.弹丸打入沙袋过程中所产生的热量为
D.沙袋和弹丸一起摆动所达到的最大高度为
BC
BD
A.左方是A球,碰撞后A、B两球速度大小之比为2∶5B.左方是A球,碰撞后A、B两球速度大小之比为1∶10C.右方是A球,碰撞后A、B两球速度大小之比为2∶5D.右方是A球,碰撞后A、B两球速度大小之比为1∶1010.如图L1-5-5所示,两质量分别为m1和m2的弹性小球1、2叠放在一起,从高度为h处自由落下,且h远大于两小球半径,所有的碰撞都是弹性碰撞,且都发生在竖直方向.已知m2=3m1,则小球1反弹后能达到的最大高度为
( )
9.如图所示,光滑水平面上有大小相同的A、B两球在同一直线上运动.两球质量关系为mB=2mA,规定向右为正方向,A、B两球的动量大小均为6 kg·m/s,运动中两球发生碰撞,碰撞后A球的动量增量为-4 kg·m/s,则 ( )
A.h B.2hC.3h D.4h
A
D
11.(多选) 如图甲所示,在光滑水平面上的两小球发生正碰,小球A、B的质量分别为m1和m2,图乙为它们碰撞前后的x-t(位移—时间)图像.已知m1=0.1 kg.由此可以判断( )
A.碰前两小球都向右运动B.碰后两小球都向右运动C.m2=0.3 kgD.碰撞过程中系统机械能守恒
12.如图所示,木块A、B、C置于光滑的水平面上,B和C之间用一轻质弹簧相连接,整个装置处于静止状态.现给A一初速度,使其沿B、C连线向B运动,随后与B相碰并粘在一起,则下列说法正确的是( )
A.A与B碰撞过程,二者组成的系统动量守恒,机械能守恒B.A与B碰撞过程,二者组成的系统动量守恒,机械能不守恒C.A与B一起压缩弹簧过程,A、B、C及弹簧组成系统动量不守恒,机械能守恒D.A与B一起压缩弹簧过程,A、B、C及弹簧组成系统动量守恒,机械能不守恒
CD
B
13.在同一竖直平面内,3个完全相同的小钢球悬挂于同一高度;静止时小球恰能接触且悬线平行,如图所示.在下列实验中,悬线始终保持绷紧状态,碰撞均为对心正碰.以下分析正确的是( )
A.将1号移至高度h释放,碰撞后,观察到2号静止、3号摆至高度h.若2号换成质量不同的小钢球,重复上述实验,3号仍能摆至高度hB.将1、2号一起移至高度h释放,碰撞后,观察到1号静止,2、3号一起摆至高度h,释放后整个过程机械能和动量都守恒C.将右侧涂胶的1号移至高度h释放,1、2号碰撞后粘在一起,根据机械能守恒,3号仍能摆至高度hD.将1号和右侧涂胶的2号一起移至高度h释放,碰撞后,2、3号粘在一起向右运动,未能摆至高度h,释放后整个过程机械能和动量都不守恒
D
14.质量相等的三个物块在一光滑水平面上排成一直线,且彼此隔开了一定的距离,如图所示.具有动能E0的第1个物块向右运动,依次与其余两个静止物块发生碰撞,最后这三个物块粘在一起,则最后这个整体的动能为
15.如图所示,一轻质弹簧两端分别连着质量均为m的滑块A和B,两滑块都置于光滑的水平面上.今有质量为m/4的子弹以水平速度v0射入A中不再穿出(时间极短),则弹簧在什么状态下滑块B具有最大动能 其值是多少
E0/3
易错为:m()2
应该为弹簧恢复原长时B的动能最大,为弹性碰撞的结果:m(·)2
谢谢 再见!
第一章 动量守恒定律
1.5.1 弹性碰撞和非弹性碰撞
碰撞是自然界常见的现象。碰撞瞬间系统动量守恒,碰撞还有什么特点?
高速飞行的陨石撞击地球,对地表产生极大的破坏;
这节课我们将从形变的角度来看碰撞系统动能特点
新课引入
网球受球拍撞击后反弹后,形状完全保持不变。
掘进机撞击地面,地面钻出一个大窟窿······
1、碰撞:是指存在相对运动的物体相遇时,在极短时间内,它们的运动状态发生显著变化的过程。
一、碰撞及碰撞的分类:
(2)碰撞的v-t图像
t1时刻相遇
t2时刻共速
t3时刻A反向
t4时刻分离
(1)碰撞的特点:内力远大于外力,碰撞物体相互作用瞬间动量守恒。
碰撞之前 碰撞之后
①正碰(对心碰撞):
②斜碰(非对心碰撞)
碰撞前后速度方向与两球心连线在同一条直线上也称一维碰撞
碰撞前后速度方向与两球心连线不在同一条直线上也称作二维碰撞
碰撞之前 碰撞之后
(1) 按碰撞前后速度方向的关系分类
【注意】本章范围内,未作特别说明时的碰撞都为正碰。
若碰撞时动能无损失,速度始终共线的碰撞常称为弹性正碰
2、 碰撞的分类
碰撞的形变恢复情况模拟视频1
碰撞的形变恢复情况模拟视频2
碰撞的形变恢复情况模拟视频3
①弹性碰撞
②非弹性碰撞
③完全非弹性碰撞
(2)按形变是否能够恢复
形变可以完全恢复
形变不能完全恢复
形变完全不能恢复
(1)系统动能不变原因:
①形变能完全恢复,位移相同X=X'
②外力忽略不计,内力对系统不做功WF+WF'=-F·X+F'·X'=ΔEK系统=0
系统动能不变.
m1
m2
v'1
v'2
X=X'
F=F'
v1
m1
m2
v2
x
F'
F
x'
二、弹性碰撞
1.弹性碰撞定义:形变量能完全恢复,碰撞前后系统总动能几乎不变的碰撞
(2)弹性碰撞的v-t图像:
m1=m2
(3)弹性碰撞的生活实例:
铁球之间、玻璃球之间以较小速度碰撞时,可视为弹性碰撞
动量守恒
动能守恒
解得2
v‘1 如何?1、2、1;2、2、2; v‘2 如何?角标互换;1换2,2换1
若m1=m2,v‘1 =v2 ; v‘2 =v1 m1和m2交换速度。
(4)弹性碰撞一般规律:
解得1
运动物体和静止物体发生弹性正碰的特点
【注意】m1碰撞静止的m2时,无论m1、m2大小关系如何总有:v1<v0 ;
碰后两球速度交换,且v1=0 ,v2=v0
①若m1=m2
②若m1>m2m2
④若m1<m2
碰后两球同向运动运动,且v1<v0<v2
碰后两球反向运动运动,且v2<v1<v0
(5)弹性碰撞特殊规律:(运动碰静止)
③若m1>>m2
碰后两球同向运动运动,且v1≈v0<v2=2v0
⑤若m1<<m2
碰后两球反向运动运动,且v2≈0<v1≈v0
解得
m2
m1
v'1
v'2
(1)动能减少原因:
①形变不能完全恢复,位移不相同X>X'
②外力忽略,系统内力做负功
WF+WF'=-F·X+F'·X'=-F·ΔX=ΔEK系统<0, 系统动能减少.
(3)非弹性碰撞规律:
x'
F
F'
X>X'
F=F'
v1
m1
m2
v2
x
Δx
1、定义:形变量不能完全恢复,碰撞前后系统总动能有明显减少的碰撞
(2)非弹性碰撞的v-t图像:
②动能减少
①动量守恒
m1=m2
三、非弹性碰撞
木球间碰撞,可视为非弹性碰撞
m2
m1
(1)动能损失最多原因:
①形变完全不能恢复,相对位移ΔX最大
②外力可忽略,内力做负功最多
WF+WF'=-F·X+F'·X'=-F·ΔX=ΔEK系统<0系统动能损失最大.
x'
v
ΔX=X-X'最大
F=F'
v1
m1
m2
v2
x
Δx
F'
F
1、定义:形变量完全不能恢复,碰撞前后系统总动能损失最多的碰撞
(2)完全非弹性碰撞的v-t图像:
m1=m2
四、完全非弹性碰撞
(3)完全非弹性碰撞的生活实例:
子弹击打木块时,形变量完全不能恢复,可视为完全非弹性碰撞
若v2=0,则
若v2=0且m+M=nm
当n→∞时,
v共=0;
Ek=0 ;
ΔEk=Ek0
(3)完全非弹性碰撞的一般规律
(4)完全非弹性碰撞的特殊规律
①
②
③
3、碰撞三原则
(1)动量守恒
(2)动能不增加:
(3)速度要合理:
①碰前同向运动,碰前:v后>v前,若碰后未反向,碰后:v后≤v后
②碰前相向运动,碰后至少一个物体方向改变。
三种碰撞规律总结
【例题1】两球A、B在光滑水平面上沿同一直线、同一方向运动, mA=1 kg, mB=2 kg, vA=6 m/s, vB=2 m/s。当A追上B并发生碰撞后,两球A、B速度的可能值是( )。
A.vA'=5 m/s,vB'=2.5 m/s B.vA'=2 m/s,vB'=4 m/s
C.vA'=-4 m/s,vB'=7 m/s D.vA'= 3m/s,vB'=3.5 m/s
BD
五、碰撞规律定性判断
题型1、速度可能性判断
【变式训练】质量为m速度为v的A球,跟质量为3m的静止B球发生正碰,碰撞可能是弹性,也可能非弹性,碰后B球的速度可能为( )
A 0.6v B 0.4v C 0.2v D0.1v
B
三原则使用优先顺序:
①先动量守恒和速度合理,
②后动能不增加,先简单运算后复杂运算
【变式训练】如图所示,光滑水平面上有大小相同的A、B两球在同一直线上运动.两球质量关系为mB=2mA,规定向右为正方向,A、B两球的动量大小均为6 kg·m/s,运动中两球发生碰撞,碰撞后A球的动量增量为-4 kg·m/s,则( )
A
A.左方是A球,碰撞后A、B两球速度大小之比为2∶5B.左方是A球,碰撞后A、B两球速度大小之比为1∶10C.右方是A球,碰撞后A、B两球速度大小之比为2∶5D.右方是A球,碰撞后A、B两球速度大小之比为1∶10
【例题3】(多选) 质量相等的A、B两球在光滑水平桌面上沿同一直线、同一方向运动,A球的动量是7kg·m/s,B球的动量是5kg·m/s,A 球追上B球发生碰撞,碰撞后两球的动量可能值是( )
A.P'A=6 kg·m/s , p'B=6 kg·m/s B.P'A=3 kg·m/s , p'B=9kg·m/s
C.P'A=5kg·m/s , p'B=7kg·m/s D.P'A=-2kg·m/s , p'B=10kg·m/s
AC
题型2、动量可能性判断
【变式训练】光滑水平面上,动能为E0 ,动量大小为p0 的小钢球1与静止的小钢球2发生弹性碰撞,碰后球1的运动反向,碰后球1的动能和动量大小分别记为 E1、p1,球2的动能和动量大小分别记为E2、p2,则必有 ( )
A. E1 < E0 B. p1 < p0
C. E2 > E0 D. p2 > p0
ABD
v0
1
2
3.解释碰撞球现象
【现象解释】
排列碰撞处理方法:碰撞按相互接触的顺序“一对一”依次发生.
相互作用力有明显大小之分,间接接触的作用力较小可忽略,
不能简单处理为“一对多”和“多对多”,除非粘贴在一起。
→v0
1
2
3
4
5
→v0
1
2
3
4
5
→v0
1
2
3
4
5
【1】
→v0
1
2
3
4
5
【2】
→v0
1
2
3
4
5
→v0
1
2
3
4
5
→v0
1
2
3
4
5
【3】
→v0
1
2
3
4
5
【4】
【例题1】(多选)如图甲所示,在光滑水平面上的两小球发生正碰。小球的质量分别为m1和m2。图乙为它们碰撞前后的s-t(位移一时间)图象。已知 m1=0.1 kg。由此可以判断( )
A. 碰前 m2 静止,m1 向右运动
B. 碰后 m2 和 m1 都向右运动
C. m2 = 0.3 kg
D. 碰撞过程中系统损失了 0.4 J 的机械能
AC
六、碰撞规律的定量求值
1.碰撞的图像问题
【例题1】如图所示,一质量为m的子弹以初速度v0水平击中静止于水平地面上的木块并没有击穿,求木块质量分别为2.5m、10m、100m时,子弹和木块因相对运动而产生的内能多大?
2.完全非弹性碰撞规律应用
【例题1】速度为10m/s的塑料球与静止的钢球发生正碰,钢球的质量是塑料球的4倍,碰撞是弹性的,求碰撞后两个小球的速度.
解:由于是弹性碰撞
与塑料球初速度方向相反
与塑料球初速度方向相同
3.特殊弹性碰撞规律应用
【例题2】一 种未知粒子跟静止的氢原子核正碰,测出碰撞后氢原子核的速度3.3×107m/s.该未知粒子跟静止的氮原子核正碰时,测出碰撞后氮原子核的速度是4.4×106m/s.已知氢原子核的质量是mH,氮原子核的质量是14mH,上述碰撞都是弹性碰撞,求未知粒子的质量.
解:设未知粒子质量m,速度v,它与氢和氮原子核碰撞都是弹性碰撞,
解①②两式,得未知粒子的质量为m=mH
①
②
【例题1】如图所示,两质量分别为m和3m的弹性小球叠放在一起,从高度为h处自由下落,且h远大于两球半径,所有碰撞都是弹性碰撞,且都发生在竖直方向,则m质量的小球反弹后能够达到的高度为 ( )
A. h B. 2h
C. 3h D. 4h
m
3m
↓
-
h
D
4.弹性碰撞规律综合应用
m
m
↓
-
h
谢谢 再见!
5 弹性碰撞和非弹性碰撞
知识点一 弹性碰撞和非弹性碰撞
1.(多选)下列关于碰撞的理解正确的是 ( )A.碰撞是指相对运动的物体相遇时,在极短时间内它们的运动状态发生了显著变化的过程B.在碰撞现象中,一般内力都远大于外力,所以可以认为碰撞时系统的动量守恒C.如果碰撞过程中机械能守恒,这样的碰撞叫作非弹性碰撞D.微观粒子的相互作用由于不发生直接接触,所以不能称其为碰撞2.(多选) 动能相同的A、B两球(mA>mB)在光滑的水平面上相向运动,两球相碰后,若其中一球停止运动,则可判定( )A.碰撞前A球的速度小于B球的速度B.碰撞前A球的动量大于B球的动量C.碰撞前后A球的动量变化量大于B球的动量变化量D.碰撞后A球的速度一定为零,B球朝反方向运动
AB
ABD
3.(多选)甲物体在光滑水平面上的运动速度为v1,与静止的乙物体相碰,碰撞过程中无机械能损失.下列结论正确的是( )A.乙的质量等于甲的质量时,碰撞后乙的速度为v1B.乙的质量远远小于甲的质量时,碰撞后乙的速度为2v1C.乙的质量远远大于甲的质量时,碰撞后甲的速度为-v1D.碰撞过程中甲对乙做的功大于乙的动能增量
4.一中子(质量数为1)与一质量数为A(A>1)的原子核发生弹性正碰.若碰前原子核静止,则碰撞前与碰撞后中子的速率之比为( )
ABC
A
5.如图所示,细线上端固定于O点上,其下端系一小球,静止时细线长为L.现将细线和小球拉至图中实线位置, 此时细线与竖直方向的夹角为θ=60°,并在小球原来所在的最低点放置一质量相同的泥球,然后使悬挂的小球从实线位置由静止释放,它运动到最低点时与泥球碰撞并合为一体,它们一起摆动中可达到的最大高度是( )
A.L/2 B.L/4 C.L/8 D.L/16
知识点二 碰撞的可行性6.(多选)质量相等的A、B两球在光滑水平面上沿同一直线向同一方向运动,A球的动量是7 kg·m/s,B球的动量是5 kg·m/s,A球追上B球发生碰撞,则碰撞后A、B两球的动量可能为( )A.p'A=8 kg·m/s,p'B=4 kg·m/sB.p'A=6 kg·m/s,p'B=6 kg·m/sC.p'A=5 kg·m/s,p'B=7 kg·m/sD.p'A=-2 kg·m/s,p'B=14 kg·m/s
C
BC
7.(多选)光滑的水平面上有A、B两个小球,其中A球的动量为10kg·m/s,
B球的动量为12 kg·m/s,A球追上B球并相碰,碰撞后,A球动量变为8 kg·m/s,方向没变,则A、B两球质量之比可能为( )
A.0.5 B.0.6 C.0.65 D.0.75
8.(多选)如图所示,一沙袋用无弹性轻细绳悬于O点.开始时沙袋处于静止状态,一弹丸以水平速度v0击中沙袋后未穿出,二者共同摆动.已知弹丸质量为m,沙袋质量为5m,弹丸和沙袋形状大小忽略不计,弹丸击中沙袋后漏出的沙子质量忽略不计,不计空气阻力,重力加速度为g.下列说法中正确的是( )
A.弹丸打入沙袋前后,细绳所受拉力大小保持不变B.弹丸打入沙袋过程中,弹丸对沙袋的冲量大小
等于沙袋对弹丸的冲量大小
C.弹丸打入沙袋过程中所产生的热量为
D.沙袋和弹丸一起摆动所达到的最大高度为
BC
BD
A.左方是A球,碰撞后A、B两球速度大小之比为2∶5B.左方是A球,碰撞后A、B两球速度大小之比为1∶10C.右方是A球,碰撞后A、B两球速度大小之比为2∶5D.右方是A球,碰撞后A、B两球速度大小之比为1∶1010.如图L1-5-5所示,两质量分别为m1和m2的弹性小球1、2叠放在一起,从高度为h处自由落下,且h远大于两小球半径,所有的碰撞都是弹性碰撞,且都发生在竖直方向.已知m2=3m1,则小球1反弹后能达到的最大高度为
( )
9.如图所示,光滑水平面上有大小相同的A、B两球在同一直线上运动.两球质量关系为mB=2mA,规定向右为正方向,A、B两球的动量大小均为6 kg·m/s,运动中两球发生碰撞,碰撞后A球的动量增量为-4 kg·m/s,则 ( )
A.h B.2hC.3h D.4h
A
D
11.(多选) 如图甲所示,在光滑水平面上的两小球发生正碰,小球A、B的质量分别为m1和m2,图乙为它们碰撞前后的x-t(位移—时间)图像.已知m1=0.1 kg.由此可以判断( )
A.碰前两小球都向右运动B.碰后两小球都向右运动C.m2=0.3 kgD.碰撞过程中系统机械能守恒
12.如图所示,木块A、B、C置于光滑的水平面上,B和C之间用一轻质弹簧相连接,整个装置处于静止状态.现给A一初速度,使其沿B、C连线向B运动,随后与B相碰并粘在一起,则下列说法正确的是( )
A.A与B碰撞过程,二者组成的系统动量守恒,机械能守恒B.A与B碰撞过程,二者组成的系统动量守恒,机械能不守恒C.A与B一起压缩弹簧过程,A、B、C及弹簧组成系统动量不守恒,机械能守恒D.A与B一起压缩弹簧过程,A、B、C及弹簧组成系统动量守恒,机械能不守恒
CD
B
13.在同一竖直平面内,3个完全相同的小钢球悬挂于同一高度;静止时小球恰能接触且悬线平行,如图所示.在下列实验中,悬线始终保持绷紧状态,碰撞均为对心正碰.以下分析正确的是( )
A.将1号移至高度h释放,碰撞后,观察到2号静止、3号摆至高度h.若2号换成质量不同的小钢球,重复上述实验,3号仍能摆至高度hB.将1、2号一起移至高度h释放,碰撞后,观察到1号静止,2、3号一起摆至高度h,释放后整个过程机械能和动量都守恒C.将右侧涂胶的1号移至高度h释放,1、2号碰撞后粘在一起,根据机械能守恒,3号仍能摆至高度hD.将1号和右侧涂胶的2号一起移至高度h释放,碰撞后,2、3号粘在一起向右运动,未能摆至高度h,释放后整个过程机械能和动量都不守恒
D
14.质量相等的三个物块在一光滑水平面上排成一直线,且彼此隔开了一定的距离,如图所示.具有动能E0的第1个物块向右运动,依次与其余两个静止物块发生碰撞,最后这三个物块粘在一起,则最后这个整体的动能为
15.如图所示,一轻质弹簧两端分别连着质量均为m的滑块A和B,两滑块都置于光滑的水平面上.今有质量为m/4的子弹以水平速度v0射入A中不再穿出(时间极短),则弹簧在什么状态下滑块B具有最大动能 其值是多少
E0/3
易错为:m()2
应该为弹簧恢复原长时B的动能最大,为弹性碰撞的结果:m(·)2
谢谢 再见!
