沪科版九年级上册22.2.5相似三角形的综合应用 课件(共15张PPT)
文档属性
| 名称 | 沪科版九年级上册22.2.5相似三角形的综合应用 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 550.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-20 19:12:46 | ||
图片预览



文档简介
(共15张PPT)
相似三角形的综合应用
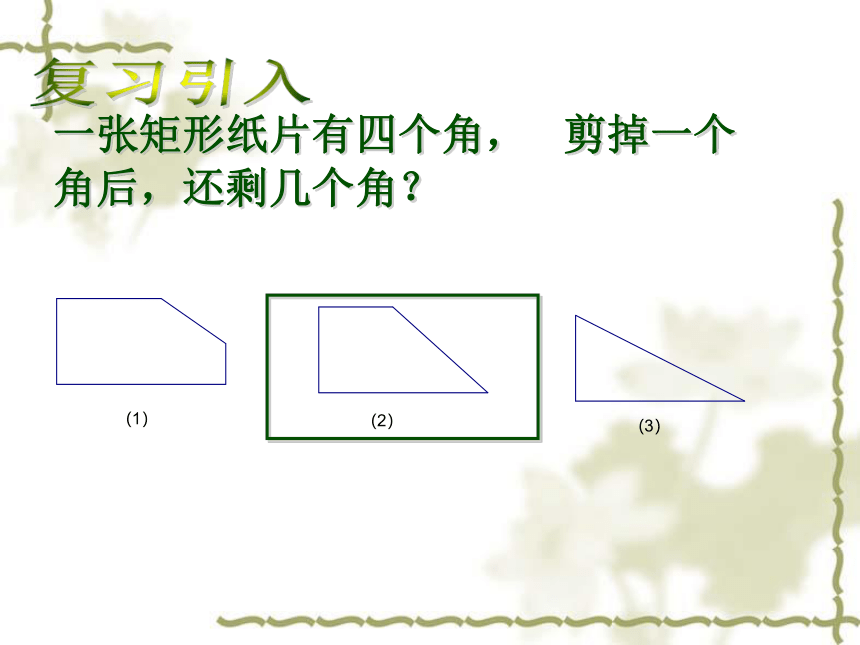
一张矩形纸片有四个角, 剪掉一个角后,还剩几个角?
一、概念中的分类讨论
三、运动变化中的分类讨论
四、含参变量的分类讨论
二、图形不确定的分类讨论
一.与概念有关的分类
1. 一次函数y=kx+b的自变量的取值范围是
-3≤x≤ 6,,相应的函数值的取值范围是
-5≤y≤-2 ,则这个函数的解析式 。
-5=-3k+b
-2=6k+b
-5=6k+b
-2=-3k+b
解析式为 Y= x-4, 或 y=- x-3
2. 函数y=ax2-ax+3x+1与x轴只有一个交点,求a的值与交点坐标。
当a=0时,为一次函数y=3x+1,交点为(- ,0);
当a不为0时,为二次函数y=ax2+(3-a)x+1, △ =a2 -10a+9=0.
解得a=1或 a=9,交点为(-1,0)或( ,0)
C
B
A
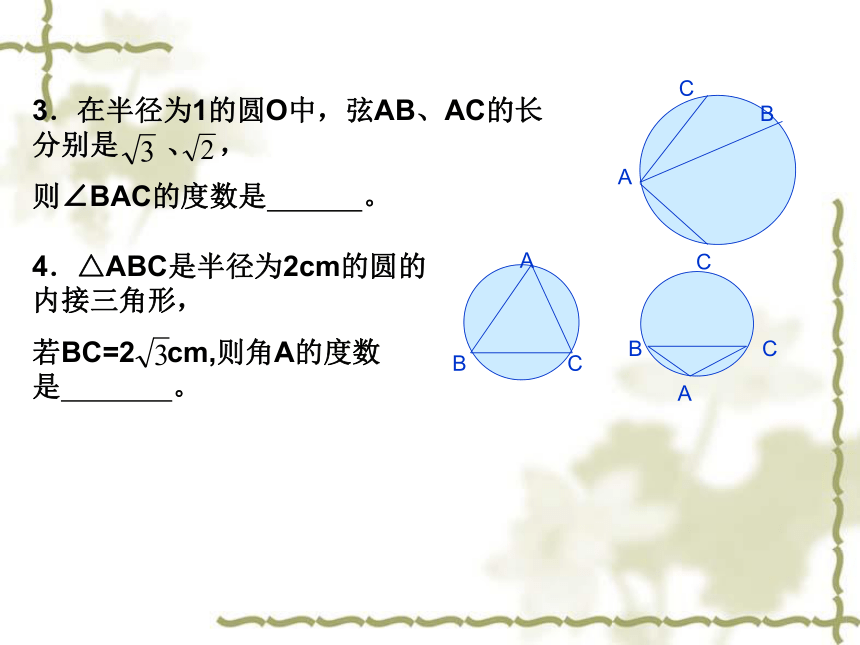
3.在半径为1的圆O中,弦AB、AC的长分别是 、 ,
则∠BAC的度数是 。
4.△ABC是半径为2cm的圆的内接三角形,
若BC=2 cm,则角A的度数是 。
C
A
B
C
C
B
A
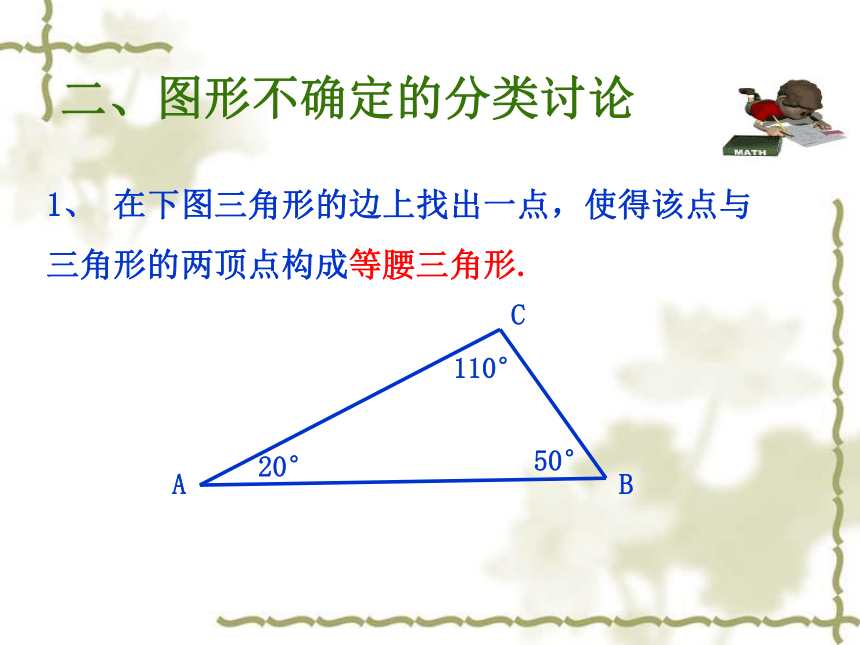
1、 在下图三角形的边上找出一点,使得该点与
三角形的两顶点构成等腰三角形.
A
C
B
50°
110°
20°
二、图形不确定的分类讨论
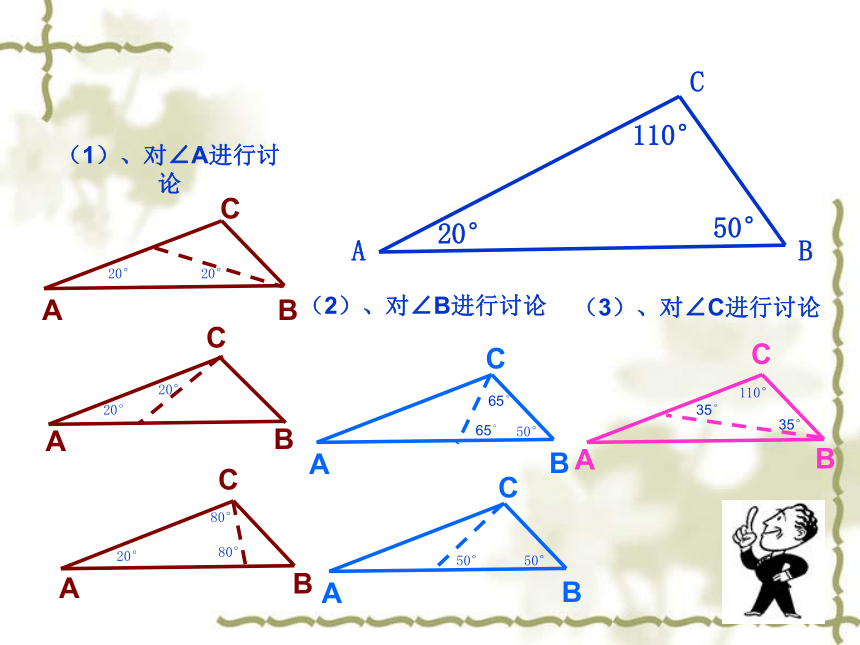
(1)、对∠A进行讨论
(2)、对∠B进行讨论
(3)、对∠C进行讨论
C
A
B
A
C
B
20°
20°
20°
20°
C
A
B
50°
50°
C
A
B
80°
80°
20°
C
A
B
65°
65°
50°
C
A
B
35°
35°
110°
A
C
B
50°
110°
20°
2、 如图,线段OD的一个端点O在直线a上,以OD为一边画等腰三角形,并且使另一个顶点在直线a上,这样的等腰三角形能画多少个
O
D
150°
⌒
C
a
E
F
H
A
A
B
C
3、△ABC中,AB=AC,AB的中垂线与AC所在的直线相交所得的锐角为40度,则底角B的度数为 。
40°
65°
A
B
C
40°
25°
1、 如图,△ABC中,AB=AC=5,BC=6,点P从A出发,沿AB以每秒1cm的速度向B运动,同时,点Q从点B出发,沿BC以相同速度向C运动,问,当 几秒后,△PBQ为直角三角形?
A
B
C
P
Q
C
A
B
P
Q
H
思考:
(1)、△PQB为直角三角形,哪些角为直角?
(2)、分类讨论∠PQB=Rt ∠ 与∠QPB=Rt ∠ 的情况:
∠PQB=Rt ∠ 或∠QPB=Rt ∠
解: 当∠PQB=Rt ∠ 时:
过A作AH⊥BC,垂足为H(如图),那么PQ∥AH.
∵ AB=AC=5,BC=6, AH⊥BC,
∴ BH=3,由勾股定理得:AH=4.
设运动的时间为 t 秒,那么AP=BQ= t ,BP=5 – t.
∵ PQ∥AH,
∴
BP
BA
=
BQ
BH
5 - t
5
=
t
3
即
t
=
15
8
解得:
t
5 - t
t
三、运动变化中的分类讨论
运动
Q
P
A
D
C
B
(3)根据题意,可分为两种情况来研究
①当 = 时,△QAP∽△ABC,则 = ,解得t= =1.2(秒)。
∴当t=1.2秒时,△QAP∽△ABC。
②当 = 时,△PAQ∽△ABC,则 = ,解得t=3(秒)。
∴当t=3秒时,△PAQ∽△ABC。
∴当t=1.2秒或t=3秒时,以点Q、A、P为顶点的三角形与三角形ABC相似。
2、在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A出发向B以2cm秒的速度移动;点Q沿DA边从点D开始向A以1cm/秒的速度移动时,如果P、Q同时出发,用t秒表示移动的时间(0<t<6)那么:
当t为何值时,以点Q、A、P
为顶点的三角形与三角形ABC相似?
1、解关于x 的方程:ax - 1= x;
解:
ax – x = 1;
(a – 1)x = 1;
x =
a – 1
1
(1) 当a =1时;此方程无解;
(2) 当a ≠1时;方程的解为:
四、含参变量的分类讨论
2.若直线:y = 4x +b 不经过第二象限,那么b的取值范围为 ;
(1)不经过第二象限,那可以只经过第一、三象限,此时 b = 0;
(2)不经过第二象限,也可以经过第一、三、四象限,此时 b < 0.
b ≤ 0
也可以用图象来直观地解决这问题:
x
y
3、某班四个小组的人数如下:10、10、x、8 已知这组数据的中位数和平均数相等.
则 x = _______.
点拨:涉及到中位数,与参数x的排列位置有关. 这样,存在几种,分别加以讨论.
若x≤8,则中位情况数为9,平均数为9,则x=8
若8≤x≤10,则中位数为(10+x)/2,平均数为(10+10+x+8)/4, 得(10+x)/2= (10+10+x+8)/4, x=8
若x≥10, 则中位数为10, 平均数为10, x=12
8或12
1、先明确需讨论的对象;
2、选择分类的标准,合理分类;
(统一标准,不重不漏)
3、逐类讨论;
4、归纳作出结论。
分类讨论思想解决问题的一般步骤:
统一标准,不重不漏
相似三角形的综合应用
一张矩形纸片有四个角, 剪掉一个角后,还剩几个角?
一、概念中的分类讨论
三、运动变化中的分类讨论
四、含参变量的分类讨论
二、图形不确定的分类讨论
一.与概念有关的分类
1. 一次函数y=kx+b的自变量的取值范围是
-3≤x≤ 6,,相应的函数值的取值范围是
-5≤y≤-2 ,则这个函数的解析式 。
-5=-3k+b
-2=6k+b
-5=6k+b
-2=-3k+b
解析式为 Y= x-4, 或 y=- x-3
2. 函数y=ax2-ax+3x+1与x轴只有一个交点,求a的值与交点坐标。
当a=0时,为一次函数y=3x+1,交点为(- ,0);
当a不为0时,为二次函数y=ax2+(3-a)x+1, △ =a2 -10a+9=0.
解得a=1或 a=9,交点为(-1,0)或( ,0)
C
B
A
3.在半径为1的圆O中,弦AB、AC的长分别是 、 ,
则∠BAC的度数是 。
4.△ABC是半径为2cm的圆的内接三角形,
若BC=2 cm,则角A的度数是 。
C
A
B
C
C
B
A
1、 在下图三角形的边上找出一点,使得该点与
三角形的两顶点构成等腰三角形.
A
C
B
50°
110°
20°
二、图形不确定的分类讨论
(1)、对∠A进行讨论
(2)、对∠B进行讨论
(3)、对∠C进行讨论
C
A
B
A
C
B
20°
20°
20°
20°
C
A
B
50°
50°
C
A
B
80°
80°
20°
C
A
B
65°
65°
50°
C
A
B
35°
35°
110°
A
C
B
50°
110°
20°
2、 如图,线段OD的一个端点O在直线a上,以OD为一边画等腰三角形,并且使另一个顶点在直线a上,这样的等腰三角形能画多少个
O
D
150°
⌒
C
a
E
F
H
A
A
B
C
3、△ABC中,AB=AC,AB的中垂线与AC所在的直线相交所得的锐角为40度,则底角B的度数为 。
40°
65°
A
B
C
40°
25°
1、 如图,△ABC中,AB=AC=5,BC=6,点P从A出发,沿AB以每秒1cm的速度向B运动,同时,点Q从点B出发,沿BC以相同速度向C运动,问,当 几秒后,△PBQ为直角三角形?
A
B
C
P
Q
C
A
B
P
Q
H
思考:
(1)、△PQB为直角三角形,哪些角为直角?
(2)、分类讨论∠PQB=Rt ∠ 与∠QPB=Rt ∠ 的情况:
∠PQB=Rt ∠ 或∠QPB=Rt ∠
解: 当∠PQB=Rt ∠ 时:
过A作AH⊥BC,垂足为H(如图),那么PQ∥AH.
∵ AB=AC=5,BC=6, AH⊥BC,
∴ BH=3,由勾股定理得:AH=4.
设运动的时间为 t 秒,那么AP=BQ= t ,BP=5 – t.
∵ PQ∥AH,
∴
BP
BA
=
BQ
BH
5 - t
5
=
t
3
即
t
=
15
8
解得:
t
5 - t
t
三、运动变化中的分类讨论
运动
Q
P
A
D
C
B
(3)根据题意,可分为两种情况来研究
①当 = 时,△QAP∽△ABC,则 = ,解得t= =1.2(秒)。
∴当t=1.2秒时,△QAP∽△ABC。
②当 = 时,△PAQ∽△ABC,则 = ,解得t=3(秒)。
∴当t=3秒时,△PAQ∽△ABC。
∴当t=1.2秒或t=3秒时,以点Q、A、P为顶点的三角形与三角形ABC相似。
2、在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A出发向B以2cm秒的速度移动;点Q沿DA边从点D开始向A以1cm/秒的速度移动时,如果P、Q同时出发,用t秒表示移动的时间(0<t<6)那么:
当t为何值时,以点Q、A、P
为顶点的三角形与三角形ABC相似?
1、解关于x 的方程:ax - 1= x;
解:
ax – x = 1;
(a – 1)x = 1;
x =
a – 1
1
(1) 当a =1时;此方程无解;
(2) 当a ≠1时;方程的解为:
四、含参变量的分类讨论
2.若直线:y = 4x +b 不经过第二象限,那么b的取值范围为 ;
(1)不经过第二象限,那可以只经过第一、三象限,此时 b = 0;
(2)不经过第二象限,也可以经过第一、三、四象限,此时 b < 0.
b ≤ 0
也可以用图象来直观地解决这问题:
x
y
3、某班四个小组的人数如下:10、10、x、8 已知这组数据的中位数和平均数相等.
则 x = _______.
点拨:涉及到中位数,与参数x的排列位置有关. 这样,存在几种,分别加以讨论.
若x≤8,则中位情况数为9,平均数为9,则x=8
若8≤x≤10,则中位数为(10+x)/2,平均数为(10+10+x+8)/4, 得(10+x)/2= (10+10+x+8)/4, x=8
若x≥10, 则中位数为10, 平均数为10, x=12
8或12
1、先明确需讨论的对象;
2、选择分类的标准,合理分类;
(统一标准,不重不漏)
3、逐类讨论;
4、归纳作出结论。
分类讨论思想解决问题的一般步骤:
统一标准,不重不漏
