沪科版九年级上册第23章 解直角三角形复习 课件(共19张PPT)
文档属性
| 名称 | 沪科版九年级上册第23章 解直角三角形复习 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 745.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-20 19:15:30 | ||
图片预览




文档简介
(共19张PPT)
复习课
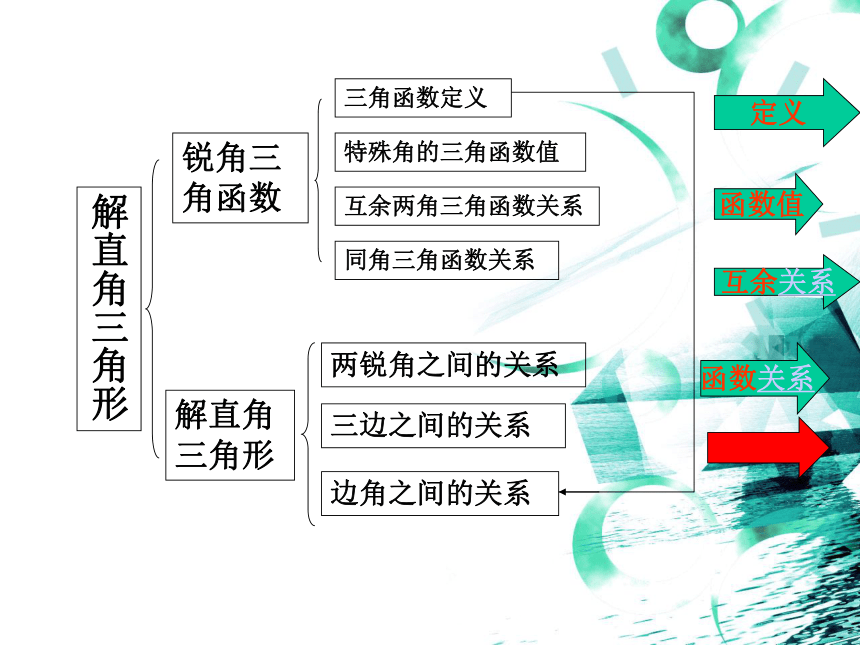
解直角三角形
锐角三角函数
解直角三角形
三角函数定义
特殊角的三角函数值
互余两角三角函数关系
同角三角函数关系
两锐角之间的关系
三边之间的关系
边角之间的关系
定义
函数值
互余关系
函数关系
A
B
C
∠A的对边
∠A的邻边
∠A的对边
∠A的邻边
tanA
cosA
∠A的邻边
∠A的对边
斜边
sinA
斜边
斜边
1.锐角A的正弦、余弦、和正切统称∠A的三角函数
定义
注意:三角函数的定义,必须在直角三角形中.
2.∠A的取值范围是什么 sinA ,cosA与tanA的取值范围又如何?
特殊角的三角函数值表
要能记住有多好
三角函数
锐角α 300 450 600
正弦sinα
余弦cosα
正切tanα
1.互余两角三角函数关系:
1.SinA=cos(900-A)
2.cosA=sin(900-A)
2.同角三角函数关系:
1.sin2A+cos2A=1
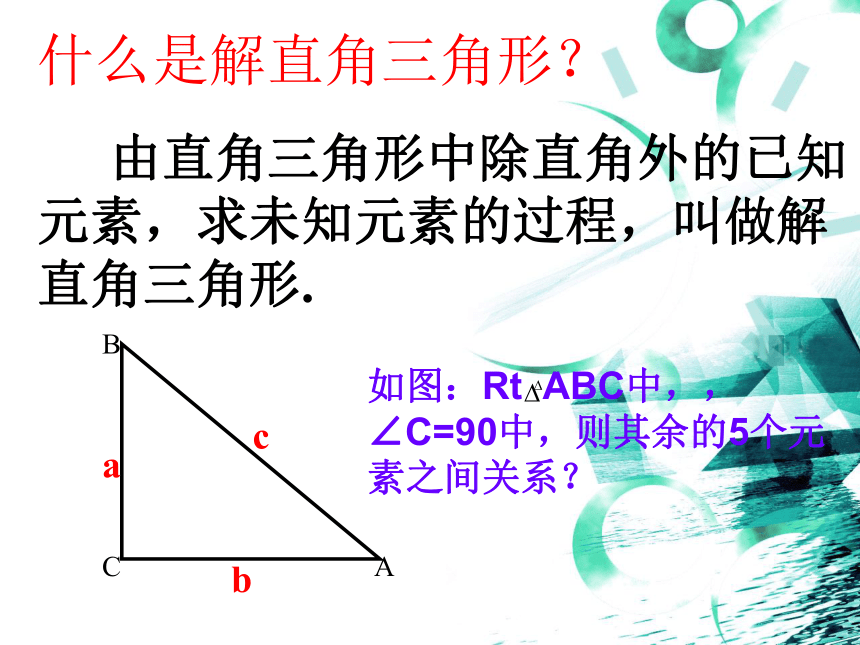
什么是解直角三角形?
由直角三角形中除直角外的已知元素,求未知元素的过程,叫做解直角三角形.
如图:Rt ABC中,,∠C=90中,则其余的5个元素之间关系?
C
A
B
b
c
a
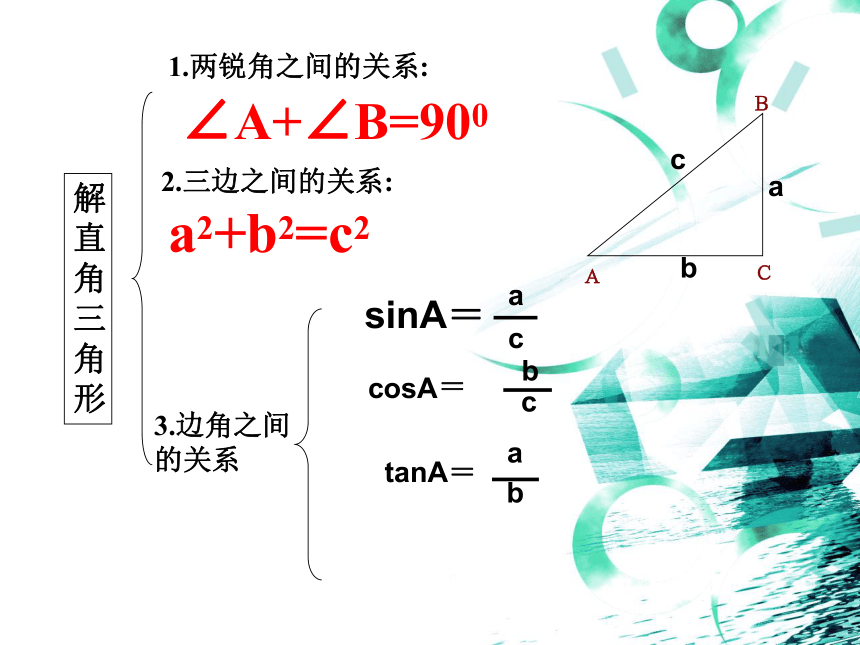
解直角三角形
1.两锐角之间的关系:
2.三边之间的关系:
3.边角之间的关系
∠A+∠B=900
a2+b2=c2
A
C
B
a
b
c
sinA=
a
c
cosA=
b
c
tanA=
a
b
在解直角三角形及应用时经常接触到的一些概念
l
h
α
(2)坡度
i =
h
l
概念反馈
(1)仰角和俯角
视线
铅垂线
水平线
视线
仰角
俯角
(3)方位角
30°
45°
B
O
A
东
西
北
南
α为坡角
=tanα
30
5.5米
A
B
C
解: 在Rt△ABC中
cosA=AC/AB
∴ AB=AC/cosA
≈6.4(米)
答:斜坡上相邻两树间的坡面距离是6.4米。
例1:山坡上种树,要求株距(相临两树间的水平
距离)是5.5米,测的斜坡倾斜角是30 ,求斜坡上相
邻两树间的坡面距离是多少米(精确到0.1米)
例2 : (北京市)如图所示,B、C是河对岸的两点,A是对岸岸边一点,测量∠ABC=45°,∠ACB=30°, BC=60米,则点A到BC的距离是 米。(精确到0.01米)
图7-3-3
21.96
D
450
300
例3. 如图所示,某地下车库的入口处有斜坡AB,其坡
度i=1∶1.5,且AB= m.
图7-3-4
C
例4、一艘船由A港沿 北偏东600方向航行10km至B 港,然后再沿北偏西300方向10km方向至C港,求
(1)A,C两港之间的距离(结果精确到0.1km);
(2)确定C港在A港什么方向.
答(1)
(2)
A
B
C
M
N
10
10
北偏东15°
例 5.如图,海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60 ,航行24海里到C,见岛A在北偏西30 ,货轮继续向西航行,有无触礁的危险?
答:货轮无触礁危险。
∵ ∠NBA= 60 , ∠N1BA= 30 ,
∴ ∠ABC=30 , ∠ACD= 60 ,
在Rt△ADC中, CD=AD tan30=
在Rt△ADB中, BD=AD tan60 =
∵ BD-CD=BC,BC=24
X= ≈12×1.732 =20.784 > 20
解:过点A作AD⊥BC于D,设AD=x
∴
∴
C
B
A
N1
N
D
1、本节例题学习以后,我们可以得到解直角三角形的两种基本图形:
A
A
B
B
C
C
D
D
2.(1)把实际问题转化成数学问题,这个转化为两个方面:一是将实际问题的图形转化为几何图形,画出正确的平面或截面示意图,二是将已知条件转化为示意图中的边、角或它们之间的关系.
(2)把数学问题转化成解直角三角形问题,如果示意图不是
直角三角形,可添加适当的辅助线,画出直角三角形.
例:如图,某货船以20海里/时的速度将一批重要物资由A处运往正西方向的B处,经16小时的航行到达,到达后必须立即卸货.此时,接到气象部门通知,一台风正以40海里/时的速度由A向北偏西60°方向移动.距台风中心200海里的圆形区域(包括边界)均会受到影响.
(1)问:B处是否受到台风的
影响 请说明理由.
(2)为避免受到台风的影响,
该船应在多少小时内卸完货物
A
B
D
北
60°
C
320
160
200
120
AC=
BD=160海里<200海里
1、理解锐角三角形函数的概念及特殊角的三角函数的值;
2、会由已知锐角求它的三角函数,由已知三角函数值求它对应的锐角 ;
3.会运用三角函数解决与直角三角形有关的简单实际问题。
课堂小结
思考:如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60° ,沿山坡向上走到P处再测得点C的仰角为45° ,已知OA=100米,山坡坡
度为 ,(即tan∠PAB= )且O、A、B在同一
条直线上。求电视塔OC的高度以及所在位置点P的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)
A
B
水平地面
C
O
山坡
60°
45°
P
E
请观察:小山的高为h,为了测的小山顶上铁塔AB
的高x,在平地上选择一点P, 在P点处测得B点的
仰角为a, A点的仰角为B.(见表中测量目标图)
P
A
B
C
a
B
X
h
题目 测量山顶铁塔的高
测量目标
已知数据
山高BC h=150米
仰角a a=45
仰角B B=30
复习课
解直角三角形
锐角三角函数
解直角三角形
三角函数定义
特殊角的三角函数值
互余两角三角函数关系
同角三角函数关系
两锐角之间的关系
三边之间的关系
边角之间的关系
定义
函数值
互余关系
函数关系
A
B
C
∠A的对边
∠A的邻边
∠A的对边
∠A的邻边
tanA
cosA
∠A的邻边
∠A的对边
斜边
sinA
斜边
斜边
1.锐角A的正弦、余弦、和正切统称∠A的三角函数
定义
注意:三角函数的定义,必须在直角三角形中.
2.∠A的取值范围是什么 sinA ,cosA与tanA的取值范围又如何?
特殊角的三角函数值表
要能记住有多好
三角函数
锐角α 300 450 600
正弦sinα
余弦cosα
正切tanα
1.互余两角三角函数关系:
1.SinA=cos(900-A)
2.cosA=sin(900-A)
2.同角三角函数关系:
1.sin2A+cos2A=1
什么是解直角三角形?
由直角三角形中除直角外的已知元素,求未知元素的过程,叫做解直角三角形.
如图:Rt ABC中,,∠C=90中,则其余的5个元素之间关系?
C
A
B
b
c
a
解直角三角形
1.两锐角之间的关系:
2.三边之间的关系:
3.边角之间的关系
∠A+∠B=900
a2+b2=c2
A
C
B
a
b
c
sinA=
a
c
cosA=
b
c
tanA=
a
b
在解直角三角形及应用时经常接触到的一些概念
l
h
α
(2)坡度
i =
h
l
概念反馈
(1)仰角和俯角
视线
铅垂线
水平线
视线
仰角
俯角
(3)方位角
30°
45°
B
O
A
东
西
北
南
α为坡角
=tanα
30
5.5米
A
B
C
解: 在Rt△ABC中
cosA=AC/AB
∴ AB=AC/cosA
≈6.4(米)
答:斜坡上相邻两树间的坡面距离是6.4米。
例1:山坡上种树,要求株距(相临两树间的水平
距离)是5.5米,测的斜坡倾斜角是30 ,求斜坡上相
邻两树间的坡面距离是多少米(精确到0.1米)
例2 : (北京市)如图所示,B、C是河对岸的两点,A是对岸岸边一点,测量∠ABC=45°,∠ACB=30°, BC=60米,则点A到BC的距离是 米。(精确到0.01米)
图7-3-3
21.96
D
450
300
例3. 如图所示,某地下车库的入口处有斜坡AB,其坡
度i=1∶1.5,且AB= m.
图7-3-4
C
例4、一艘船由A港沿 北偏东600方向航行10km至B 港,然后再沿北偏西300方向10km方向至C港,求
(1)A,C两港之间的距离(结果精确到0.1km);
(2)确定C港在A港什么方向.
答(1)
(2)
A
B
C
M
N
10
10
北偏东15°
例 5.如图,海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60 ,航行24海里到C,见岛A在北偏西30 ,货轮继续向西航行,有无触礁的危险?
答:货轮无触礁危险。
∵ ∠NBA= 60 , ∠N1BA= 30 ,
∴ ∠ABC=30 , ∠ACD= 60 ,
在Rt△ADC中, CD=AD tan30=
在Rt△ADB中, BD=AD tan60 =
∵ BD-CD=BC,BC=24
X= ≈12×1.732 =20.784 > 20
解:过点A作AD⊥BC于D,设AD=x
∴
∴
C
B
A
N1
N
D
1、本节例题学习以后,我们可以得到解直角三角形的两种基本图形:
A
A
B
B
C
C
D
D
2.(1)把实际问题转化成数学问题,这个转化为两个方面:一是将实际问题的图形转化为几何图形,画出正确的平面或截面示意图,二是将已知条件转化为示意图中的边、角或它们之间的关系.
(2)把数学问题转化成解直角三角形问题,如果示意图不是
直角三角形,可添加适当的辅助线,画出直角三角形.
例:如图,某货船以20海里/时的速度将一批重要物资由A处运往正西方向的B处,经16小时的航行到达,到达后必须立即卸货.此时,接到气象部门通知,一台风正以40海里/时的速度由A向北偏西60°方向移动.距台风中心200海里的圆形区域(包括边界)均会受到影响.
(1)问:B处是否受到台风的
影响 请说明理由.
(2)为避免受到台风的影响,
该船应在多少小时内卸完货物
A
B
D
北
60°
C
320
160
200
120
AC=
BD=160海里<200海里
1、理解锐角三角形函数的概念及特殊角的三角函数的值;
2、会由已知锐角求它的三角函数,由已知三角函数值求它对应的锐角 ;
3.会运用三角函数解决与直角三角形有关的简单实际问题。
课堂小结
思考:如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60° ,沿山坡向上走到P处再测得点C的仰角为45° ,已知OA=100米,山坡坡
度为 ,(即tan∠PAB= )且O、A、B在同一
条直线上。求电视塔OC的高度以及所在位置点P的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)
A
B
水平地面
C
O
山坡
60°
45°
P
E
请观察:小山的高为h,为了测的小山顶上铁塔AB
的高x,在平地上选择一点P, 在P点处测得B点的
仰角为a, A点的仰角为B.(见表中测量目标图)
P
A
B
C
a
B
X
h
题目 测量山顶铁塔的高
测量目标
已知数据
山高BC h=150米
仰角a a=45
仰角B B=30
