【核心素养目标】1.2二次函数的图象与性质(4) 教学设计
文档属性
| 名称 | 【核心素养目标】1.2二次函数的图象与性质(4) 教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-21 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
湘教版版九年级下册数学1.2二次函数的图象与性质(4)教学设计
课题 1.2二次函数的图象与性质(4) 单元 第一单元 学科 数学 年级 九
教材分析 熟悉二次函数y=a(x-h)2+k顶点的形式,进一步认识二次函数y=a(x-h)2+k图象的作图步骤,理解二次函数y=a(x-h)2+k的性质,解决二次函数的相关问题。
核心素养分析 学生掌握了y=a(x-h)2 的作图的过程,进一步根据图形的平移,得到二次函数y=a(x-h)2+k,锻炼学生的动手作图能力,培养学生严谨的科学素养。
学习目标 1.理解抛物线y=a(x-h)2+k由y=a(x-h)2 平移得到;2.会画y=a(x-h)2+k的图象,掌握二次函数顶点式,y=a(x-h)2+k的图象与性质;3.能用y=a(x-h)2+k的图象与性质解答二次函数问题.
重点 会画y=a(x-h)2+k的图象,掌握二次函数顶点式y=a(x-h)2+k的图象与性质
难点 能用y=a(x-h)2+k的图象与性质解答二次函数问题
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 回顾知识,让学生回答, 其他学生补充,以培养学生温顾知识,大胆发言的良好习惯. 学生回忆二次函数y=a(x-h)2 ,导入新的二次函数y=a(x-h)2+k进行知识的迁移。
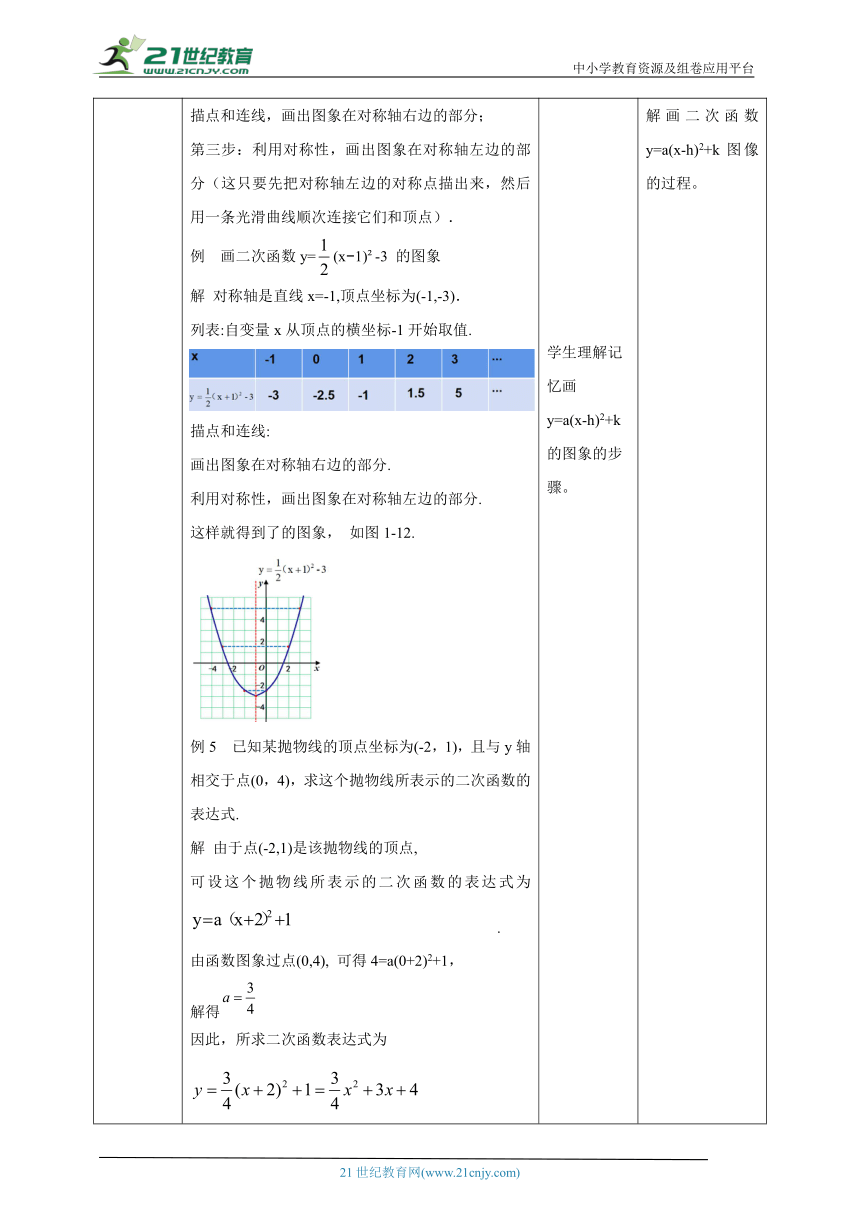
讲授新课 探究如何画二次函数y=(x 1) +3 的图象?我们已经知道y=(x 1) 的画法,以及函数的性质。我们先来探究二次函数y=(x 1) 与y=(x 1) +3 之间的关系。从上表看出:对于每一个给定的x值,函数y=(x 1) +3的值都要比函数y=(x 1) 的值大3.由此可见,函数y=(x 1) +3的图象可由二次函数 y=(x 1) 的图象向上平移3个单位而得到(如图 1-11). 二次函数y=(x 1) +3的图象特点:对称轴:直线x=1 (与抛物线y=(x 1) 的对称轴一样),顶点坐标:(1,3)(它是由抛物线y=(x 1) 的顶点(1,0)向上平移3个单位得到的);开口方向:开口向上。一般地,二次函数y=a(x-h)2+k的图象是抛物线,它具有下述性质:画y=a(x-h)2+k的图象的步骤如下: 第一步:写出对称轴和顶点坐标,并且在平面直角坐标系内画出对称轴,描出顶点; 第二步:列表(自变量x从顶点的横坐标开始取值),描点和连线,画出图象在对称轴右边的部分; 第三步:利用对称性,画出图象在对称轴左边的部分(这只要先把对称轴左边的对称点描出来,然后用一条光滑曲线顺次连接它们和顶点). 例 画二次函数y=(x 1) -3 的图象解 对称轴是直线x=-1,顶点坐标为(-1,-3). 列表:自变量x从顶点的横坐标-1开始取值.描点和连线:画出图象在对称轴右边的部分.利用对称性,画出图象在对称轴左边的部分.这样就得到了的图象, 如图1-12.例5 已知某抛物线的顶点坐标为(-2,1),且与y轴相交于点(0,4),求这个抛物线所表示的二次函数的表达式.解 由于点(-2,1)是该抛物线的顶点,可设这个抛物线所表示的二次函数的表达式为 . 由函数图象过点(0,4), 可得4=a(0+2)2+1,解得因此,所求二次函数表达式为二次函数y=x 怎样平移,能得到 y=(x 1) +3的图象呢?注意: 由 y=ax2平移得到y =a( x-h ) 2+h 的规律:“左右平移,左加右减;上下平移,上加下减” 学生独立思考、小组合作讨论,探讨两种二次函数之间的关系, 学会倾听别的同学的意见。通过对比,发现两种二次函数的关系,对比得出结论。学生理解掌握二次函数 的图象特点。学生理解记忆画y=a(x-h)2+k的图象的步骤。学生自己尝试总结二次函数平移的规律,并学会运用。 提出问题,激发学生对二次函数y=(x 1) 与y=(x 1) +3 之间的关系的探讨。学生通过对y=a(x-h)2 的作图的过程,进一步了解根据图形的平移,得到二次函数y=a(x-h)2+k。让学生从二次函数的对称轴、顶点坐标、开口方向来分析理解二次函数的特点。让学生体会、理解画二次函数y=a(x-h)2+k图像的过程。学生认识规律,掌握平移的规律,并运用二次函数平移的规律。
课堂练习 1.二次函数y=2(x-1)2-2的图象是由二次函数y=2x2的图象平移得到的,下列平移方法正确的是( )A. 先向左平移1个单位,再向上平移2个单位B. 先向左平移1个单位,再向下平移2个单位C. 先向右平移1个单位,再向上平移2个单位D. 先向右平移1个单位,再向下平移2个单位解:抛物线y=2x2的顶点坐标是(0,0).抛物线y=2(x-1)2-2的顶点坐标是(1,-2).则由二次函数y=2x2的图象向右平移1个单位,向下平移2个单位即可得到二次函数y=2(x-1)2-2的图象.故选:D.2. 关于二次函数y=-(x-2)2+9,以下说法不正确的是( )A. 图象与y轴的交点坐标为(0,9) B. 图象的对称轴为直线x=2C. 当x>2时,y随x增大而减小 D. y的最大值为9解:∵二次函数y=-(x-2)2+9,∴抛物线的对称轴是直线x=2,故B正确;∵a=-1<0,∴抛物线的开口向下,故当x=2时,y的最大值为9,故D正确,当x>2时,y的值随x值的增大而减小,故C正确,针对于二次函数y=-(x-2)2+9,令x=0,则y=5,∴图象与y轴的交点坐标为(0,5),故A错误,故选:A. 3.已知A(m,y1 ),B(4,y2 )为抛物线y=-(x-3)2+k上的两个不同点,若y1 >y2,则可知m的取值范围为( )A. m>4 B.m<2或m>4 C. m<2 D. 23时,y随x是增大而减小,顶点为最高点,∴B(4,y2)关于直线x=3的对称点为(2,y2),∵y1>y2∴2课堂小结 学生先发言总结,在教师的引导下总结归纳本节二次函数的内容。 让学生自己对本节课知识进行整合归纳,培养学生养成一种对所学知识进行总结的良好习惯,形成知识体系.
板书 课题: 1.2二次函数的图像与性质(4)1.画二次函数y=y=a(x-h)2+k的步骤:列表、描点、连线2.二次函数y=y=a(x-h)2+k的图象与性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
湘教版版九年级下册数学1.2二次函数的图象与性质(4)教学设计
课题 1.2二次函数的图象与性质(4) 单元 第一单元 学科 数学 年级 九
教材分析 熟悉二次函数y=a(x-h)2+k顶点的形式,进一步认识二次函数y=a(x-h)2+k图象的作图步骤,理解二次函数y=a(x-h)2+k的性质,解决二次函数的相关问题。
核心素养分析 学生掌握了y=a(x-h)2 的作图的过程,进一步根据图形的平移,得到二次函数y=a(x-h)2+k,锻炼学生的动手作图能力,培养学生严谨的科学素养。
学习目标 1.理解抛物线y=a(x-h)2+k由y=a(x-h)2 平移得到;2.会画y=a(x-h)2+k的图象,掌握二次函数顶点式,y=a(x-h)2+k的图象与性质;3.能用y=a(x-h)2+k的图象与性质解答二次函数问题.
重点 会画y=a(x-h)2+k的图象,掌握二次函数顶点式y=a(x-h)2+k的图象与性质
难点 能用y=a(x-h)2+k的图象与性质解答二次函数问题
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 回顾知识,让学生回答, 其他学生补充,以培养学生温顾知识,大胆发言的良好习惯. 学生回忆二次函数y=a(x-h)2 ,导入新的二次函数y=a(x-h)2+k进行知识的迁移。
讲授新课 探究如何画二次函数y=(x 1) +3 的图象?我们已经知道y=(x 1) 的画法,以及函数的性质。我们先来探究二次函数y=(x 1) 与y=(x 1) +3 之间的关系。从上表看出:对于每一个给定的x值,函数y=(x 1) +3的值都要比函数y=(x 1) 的值大3.由此可见,函数y=(x 1) +3的图象可由二次函数 y=(x 1) 的图象向上平移3个单位而得到(如图 1-11). 二次函数y=(x 1) +3的图象特点:对称轴:直线x=1 (与抛物线y=(x 1) 的对称轴一样),顶点坐标:(1,3)(它是由抛物线y=(x 1) 的顶点(1,0)向上平移3个单位得到的);开口方向:开口向上。一般地,二次函数y=a(x-h)2+k的图象是抛物线,它具有下述性质:画y=a(x-h)2+k的图象的步骤如下: 第一步:写出对称轴和顶点坐标,并且在平面直角坐标系内画出对称轴,描出顶点; 第二步:列表(自变量x从顶点的横坐标开始取值),描点和连线,画出图象在对称轴右边的部分; 第三步:利用对称性,画出图象在对称轴左边的部分(这只要先把对称轴左边的对称点描出来,然后用一条光滑曲线顺次连接它们和顶点). 例 画二次函数y=(x 1) -3 的图象解 对称轴是直线x=-1,顶点坐标为(-1,-3). 列表:自变量x从顶点的横坐标-1开始取值.描点和连线:画出图象在对称轴右边的部分.利用对称性,画出图象在对称轴左边的部分.这样就得到了的图象, 如图1-12.例5 已知某抛物线的顶点坐标为(-2,1),且与y轴相交于点(0,4),求这个抛物线所表示的二次函数的表达式.解 由于点(-2,1)是该抛物线的顶点,可设这个抛物线所表示的二次函数的表达式为 . 由函数图象过点(0,4), 可得4=a(0+2)2+1,解得因此,所求二次函数表达式为二次函数y=x 怎样平移,能得到 y=(x 1) +3的图象呢?注意: 由 y=ax2平移得到y =a( x-h ) 2+h 的规律:“左右平移,左加右减;上下平移,上加下减” 学生独立思考、小组合作讨论,探讨两种二次函数之间的关系, 学会倾听别的同学的意见。通过对比,发现两种二次函数的关系,对比得出结论。学生理解掌握二次函数 的图象特点。学生理解记忆画y=a(x-h)2+k的图象的步骤。学生自己尝试总结二次函数平移的规律,并学会运用。 提出问题,激发学生对二次函数y=(x 1) 与y=(x 1) +3 之间的关系的探讨。学生通过对y=a(x-h)2 的作图的过程,进一步了解根据图形的平移,得到二次函数y=a(x-h)2+k。让学生从二次函数的对称轴、顶点坐标、开口方向来分析理解二次函数的特点。让学生体会、理解画二次函数y=a(x-h)2+k图像的过程。学生认识规律,掌握平移的规律,并运用二次函数平移的规律。
课堂练习 1.二次函数y=2(x-1)2-2的图象是由二次函数y=2x2的图象平移得到的,下列平移方法正确的是( )A. 先向左平移1个单位,再向上平移2个单位B. 先向左平移1个单位,再向下平移2个单位C. 先向右平移1个单位,再向上平移2个单位D. 先向右平移1个单位,再向下平移2个单位解:抛物线y=2x2的顶点坐标是(0,0).抛物线y=2(x-1)2-2的顶点坐标是(1,-2).则由二次函数y=2x2的图象向右平移1个单位,向下平移2个单位即可得到二次函数y=2(x-1)2-2的图象.故选:D.2. 关于二次函数y=-(x-2)2+9,以下说法不正确的是( )A. 图象与y轴的交点坐标为(0,9) B. 图象的对称轴为直线x=2C. 当x>2时,y随x增大而减小 D. y的最大值为9解:∵二次函数y=-(x-2)2+9,∴抛物线的对称轴是直线x=2,故B正确;∵a=-1<0,∴抛物线的开口向下,故当x=2时,y的最大值为9,故D正确,当x>2时,y的值随x值的增大而减小,故C正确,针对于二次函数y=-(x-2)2+9,令x=0,则y=5,∴图象与y轴的交点坐标为(0,5),故A错误,故选:A. 3.已知A(m,y1 ),B(4,y2 )为抛物线y=-(x-3)2+k上的两个不同点,若y1 >y2,则可知m的取值范围为( )A. m>4 B.m<2或m>4 C. m<2 D. 2
板书 课题: 1.2二次函数的图像与性质(4)1.画二次函数y=y=a(x-h)2+k的步骤:列表、描点、连线2.二次函数y=y=a(x-h)2+k的图象与性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
