【核心素养目标】1.2二次函数的图象与性质(5) 教学设计
文档属性
| 名称 | 【核心素养目标】1.2二次函数的图象与性质(5) 教学设计 |
|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-21 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
湘教版版九年级下册数学1.2二次函数的图象与性质(5)教学设计
课题 1.2二次函数的图象与性质(5) 单元 第一单元 学科 数学 年级 九
教材分析 本节是二次函数表达式的最后一种,从上节学习的顶点式y=a(x-h)2+k,可以化为一般形式y=ax +bx+c,也可以从一般形式化为顶点式。一般式也有顶点坐标,本节还会学习求二次函数的最值,本节是最重要的一节。
核心素养分析 本节内容主要是二次函数y=ax +bx+c图象的顶点坐标公式的推导,学生从中学到理性推理的过程,培养学生严谨的推理的科学素养,发展学生的推理能力,抽象能力。
学习目标 1.掌握配方法把y=ax +bx+c化成y=a(x-h)2+k的形式,掌握画二次函数y=ax +bx+c图象的方法 2.会求二次函数y=ax +bx+c图象的顶点坐标公式 3.能用不同方法求y=ax +bx+c的顶点坐标和最大(小)值
重点 掌握配方法把y=ax +bx+c化成y=a(x-h)2+k的形式,掌握画二次函数y=ax +bx+c图象的方法会求二次函数y=ax +bx+c图象的顶点坐标公式
难点 能用不同方法求y=ax +bx+c的顶点坐标和最大(小)值
教学过程
教学环节 教师活动 学生活动 设计意图
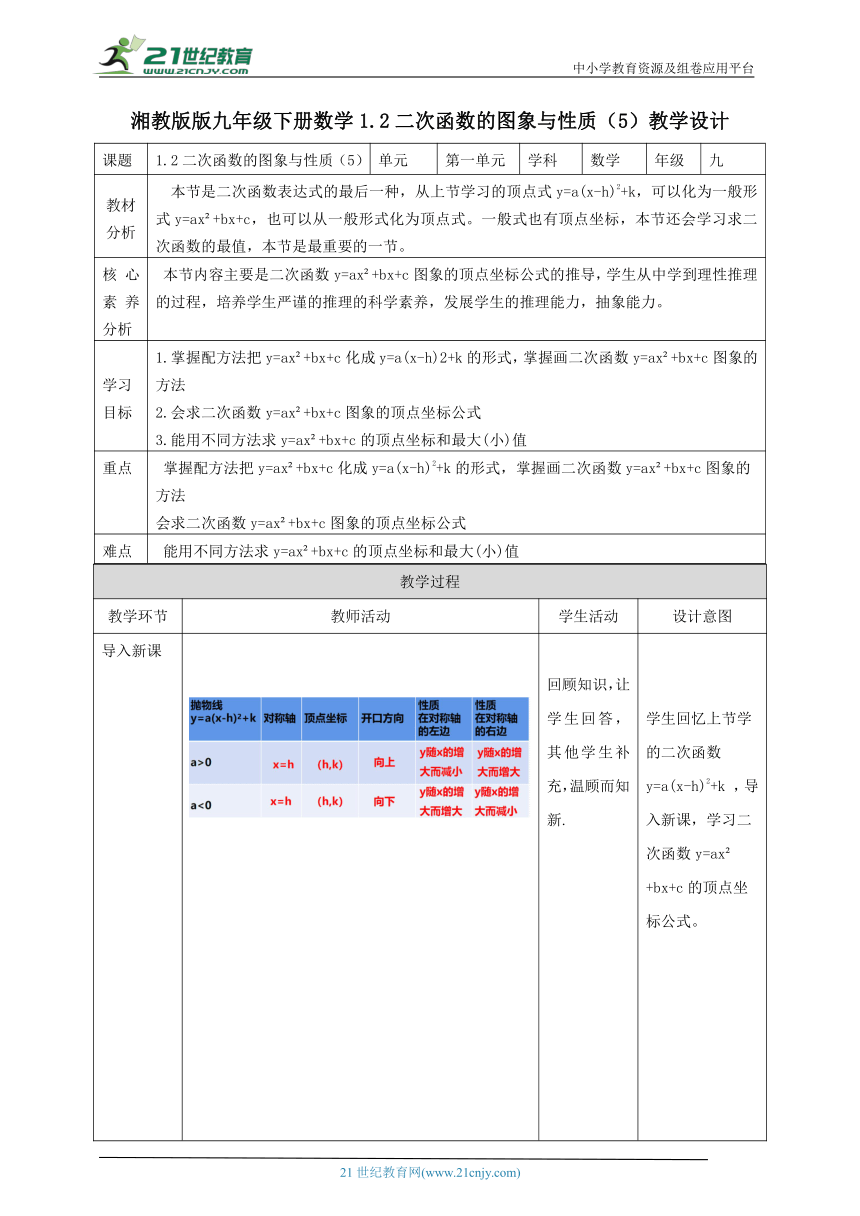
导入新课 回顾知识,让学生回答, 其他学生补充,温顾而知新. 学生回忆上节学的二次函数y=a(x-h)2+k ,导入新课,学习二次函数y=ax +bx+c的顶点坐标公式。
讲授新课 动脑筋如何画二次函数 y=-2x2+6x-1 的图象?由于我们已经会画y=a(x-h)2+k的图象了, 因此只需把y=-2x2+6x-1配方成-2(x-h)2+k的形式就可以了.配方:y=-2x2+6x-1=-2(x2-3x)-1故对称轴是直线 顶点坐标是列表:自变量x从顶点的横坐标开始取值.描点和连线:画出图象在对称轴右边的部分.利用对称性,画出图象在对称轴左边的部分,这样就得到了函数y=-2x2+6x-1的图象,如图1-13.图1-13说一说观察图1-13,当x等于多少时,函数y=-2x2+6x-1的值最大? 这个最大值是多少?当x等于顶点的横坐标 时,函数值最大,这个最大值等于顶点的纵坐标 .二次函数y=ax +bx+c,当x等于顶点的横坐标时,达到最大值(a<0)或最小值(a>0 ),这个最大(小)值等于顶点的纵坐标.例6 求二次函数 的最大值。解 顶点坐标是(2,1),于是当x=2时,y达到最大值1.一般地, 对于二次函数y=ax +bx+c进行配方:解:y=ax +bx+c顶点坐标 因此,当 时,函数达到最大值(a<0)或最小值(a>0): 注意:二次函数y=ax +bx+c,顶点坐标 当 时,函数达到最大值(a<0)或最小值(a>0): 二次函数y=ax2+bx+c,当x=0,1,2-1,-2时,求y的值?二次函数y=ax2+bx+c( a≠0)的特殊函数值.(1)x=0时,函数值为y=c.(2)x=1时,函数值为y=a+b+c.(3)x=2时,函数值为y=4a+2b+c.(4)x=-1 时,函数值为y=a-b+c.(5)x=-2时,函数值为y=4a-2b+c. 学生独立思考、小组合作讨论,学会画y=ax +bx+c图象,研究顶点坐标公式, 学会倾听别的同学的意见。学生再次学习画二次函数y=ax +bx+c的三步骤,列表描点和连线:学生理解掌握二次函数 的最值。学生总结,二次函数中,当x等于顶点的横坐标时,y有最大值或最小值。 学生自己记住顶点坐标公式,尝试运用二次函数顶点坐标公式,求对称轴,以及最值。 提出问题,激发学生学习兴趣,通过对y=ax +bx+c配方,化为学生熟悉的顶点式,研究其性质。学生经历了y=ax +bx+c的作图的过程,认识到二次函数y=ax +bx+c顶点坐标公式,对称轴等重要性质。让学生理解通过二次函数的顶点的横坐标,可以求二次函数的最值。学生熟记顶点坐标公式,运用公式解决问题。
课堂练习 1.关于二次函数y=2x2+4x-1,下列说法正确的是( )A. 图象与y轴的交点坐标为(0,1)B. 图象的对称轴在y轴的右侧C. 当x<0时,y的值随x值的增大而减小D. y的最小值为-3解:∵y=2x2+4x-1=2(x+1)2-3,∴当x=0时,y=-1,故选项A错误;该函数的对称轴是直线x=-1,故选项B错误;当x<-1时,y随x的增大而减小,故选项C错误;当x=-1时,y取得最小值,此时y=-3,故选项D正确.故选D2. 函数与在同一坐标系中的大致图象可能为( )A. B.
C. D. 解:A.由直线可知b<0,c>0,由抛物线可知a<0,b>0,c>0,故A不符合题意;B.由直线可知b<0,c>0,由抛物线可知a>0,b<0,c>0,故B符合题意;C.由直线可知b>0,c>0,由抛物线可知a>0,b<0,c>0,故C不符合题意;D.由直线可知b<0,c>0,由抛物线可知a>0,b<0,c<0,故D不符合题意. 故选B. 3.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0)和B,与y轴交于点C.下列结论:①abc<0,②2a+b<0,③4a-2b+c>0,④3a+c>0,其中正确的结论个数为( )A. 1个 B. 2个 C. 3个 D. 4个解:①∵由抛物线的开口向上知a>0,∵对称轴位于y轴的右侧, ∴b<0.∵抛物线与y轴交于负半轴, ∴c<0,∴abc>0,故错误;②对称轴为x<1,得2a>-b,即2a+b>0,故错误;③当x=-2时,y>0,4a-2b+c>0,故正确;④∵当x=-1时,y=0,∴0=a-b+c0.故正确.综上所述,有2个结论正确. 故选:B. 学生做练习,互相补充,有问题的地方教师进行订正 ,做最后总结,学生共同完成问题的解决。 练习是为了巩固学生所学的新知,并让学生学会运用二次函数顶点坐标,判断函数的性质,同时培养了学生建模的能力。
课堂小结 二次函数y=ax +bx+c配方:①提取系数:把二次项系数提到二次项和一次项前面;②加减平方数:括号内加、减一次项系数一半的平方;③去括号:写成完全平方式,去括号;④写成y=a(x+m)2+n的形式。注意:配方后得顶点坐标(-m,n),对称轴x=-m.二次函数y=ax +bx+c,顶点坐标 当时,函数达到最大值(a<0)或最小值(a>0): 学生先发言总结,在教师的引导下总结归纳本节二次函数的一般式内容。 让学生自己对本节课知识进行整合归纳,培养学生养成及时总结的习惯。
板书 课题:1.2二次函数的图像与性质(5)1.画二次函数y=ax +bx+c的步骤:列表、描点、连线2.二次函数y=ax +bx+c的图像与性质顶点坐标最值
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
湘教版版九年级下册数学1.2二次函数的图象与性质(5)教学设计
课题 1.2二次函数的图象与性质(5) 单元 第一单元 学科 数学 年级 九
教材分析 本节是二次函数表达式的最后一种,从上节学习的顶点式y=a(x-h)2+k,可以化为一般形式y=ax +bx+c,也可以从一般形式化为顶点式。一般式也有顶点坐标,本节还会学习求二次函数的最值,本节是最重要的一节。
核心素养分析 本节内容主要是二次函数y=ax +bx+c图象的顶点坐标公式的推导,学生从中学到理性推理的过程,培养学生严谨的推理的科学素养,发展学生的推理能力,抽象能力。
学习目标 1.掌握配方法把y=ax +bx+c化成y=a(x-h)2+k的形式,掌握画二次函数y=ax +bx+c图象的方法 2.会求二次函数y=ax +bx+c图象的顶点坐标公式 3.能用不同方法求y=ax +bx+c的顶点坐标和最大(小)值
重点 掌握配方法把y=ax +bx+c化成y=a(x-h)2+k的形式,掌握画二次函数y=ax +bx+c图象的方法会求二次函数y=ax +bx+c图象的顶点坐标公式
难点 能用不同方法求y=ax +bx+c的顶点坐标和最大(小)值
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 回顾知识,让学生回答, 其他学生补充,温顾而知新. 学生回忆上节学的二次函数y=a(x-h)2+k ,导入新课,学习二次函数y=ax +bx+c的顶点坐标公式。
讲授新课 动脑筋如何画二次函数 y=-2x2+6x-1 的图象?由于我们已经会画y=a(x-h)2+k的图象了, 因此只需把y=-2x2+6x-1配方成-2(x-h)2+k的形式就可以了.配方:y=-2x2+6x-1=-2(x2-3x)-1故对称轴是直线 顶点坐标是列表:自变量x从顶点的横坐标开始取值.描点和连线:画出图象在对称轴右边的部分.利用对称性,画出图象在对称轴左边的部分,这样就得到了函数y=-2x2+6x-1的图象,如图1-13.图1-13说一说观察图1-13,当x等于多少时,函数y=-2x2+6x-1的值最大? 这个最大值是多少?当x等于顶点的横坐标 时,函数值最大,这个最大值等于顶点的纵坐标 .二次函数y=ax +bx+c,当x等于顶点的横坐标时,达到最大值(a<0)或最小值(a>0 ),这个最大(小)值等于顶点的纵坐标.例6 求二次函数 的最大值。解 顶点坐标是(2,1),于是当x=2时,y达到最大值1.一般地, 对于二次函数y=ax +bx+c进行配方:解:y=ax +bx+c顶点坐标 因此,当 时,函数达到最大值(a<0)或最小值(a>0): 注意:二次函数y=ax +bx+c,顶点坐标 当 时,函数达到最大值(a<0)或最小值(a>0): 二次函数y=ax2+bx+c,当x=0,1,2-1,-2时,求y的值?二次函数y=ax2+bx+c( a≠0)的特殊函数值.(1)x=0时,函数值为y=c.(2)x=1时,函数值为y=a+b+c.(3)x=2时,函数值为y=4a+2b+c.(4)x=-1 时,函数值为y=a-b+c.(5)x=-2时,函数值为y=4a-2b+c. 学生独立思考、小组合作讨论,学会画y=ax +bx+c图象,研究顶点坐标公式, 学会倾听别的同学的意见。学生再次学习画二次函数y=ax +bx+c的三步骤,列表描点和连线:学生理解掌握二次函数 的最值。学生总结,二次函数中,当x等于顶点的横坐标时,y有最大值或最小值。 学生自己记住顶点坐标公式,尝试运用二次函数顶点坐标公式,求对称轴,以及最值。 提出问题,激发学生学习兴趣,通过对y=ax +bx+c配方,化为学生熟悉的顶点式,研究其性质。学生经历了y=ax +bx+c的作图的过程,认识到二次函数y=ax +bx+c顶点坐标公式,对称轴等重要性质。让学生理解通过二次函数的顶点的横坐标,可以求二次函数的最值。学生熟记顶点坐标公式,运用公式解决问题。
课堂练习 1.关于二次函数y=2x2+4x-1,下列说法正确的是( )A. 图象与y轴的交点坐标为(0,1)B. 图象的对称轴在y轴的右侧C. 当x<0时,y的值随x值的增大而减小D. y的最小值为-3解:∵y=2x2+4x-1=2(x+1)2-3,∴当x=0时,y=-1,故选项A错误;该函数的对称轴是直线x=-1,故选项B错误;当x<-1时,y随x的增大而减小,故选项C错误;当x=-1时,y取得最小值,此时y=-3,故选项D正确.故选D2. 函数与在同一坐标系中的大致图象可能为( )A. B.
C. D. 解:A.由直线可知b<0,c>0,由抛物线可知a<0,b>0,c>0,故A不符合题意;B.由直线可知b<0,c>0,由抛物线可知a>0,b<0,c>0,故B符合题意;C.由直线可知b>0,c>0,由抛物线可知a>0,b<0,c>0,故C不符合题意;D.由直线可知b<0,c>0,由抛物线可知a>0,b<0,c<0,故D不符合题意. 故选B. 3.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0)和B,与y轴交于点C.下列结论:①abc<0,②2a+b<0,③4a-2b+c>0,④3a+c>0,其中正确的结论个数为( )A. 1个 B. 2个 C. 3个 D. 4个解:①∵由抛物线的开口向上知a>0,∵对称轴位于y轴的右侧, ∴b<0.∵抛物线与y轴交于负半轴, ∴c<0,∴abc>0,故错误;②对称轴为x<1,得2a>-b,即2a+b>0,故错误;③当x=-2时,y>0,4a-2b+c>0,故正确;④∵当x=-1时,y=0,∴0=a-b+c
课堂小结 二次函数y=ax +bx+c配方:①提取系数:把二次项系数提到二次项和一次项前面;②加减平方数:括号内加、减一次项系数一半的平方;③去括号:写成完全平方式,去括号;④写成y=a(x+m)2+n的形式。注意:配方后得顶点坐标(-m,n),对称轴x=-m.二次函数y=ax +bx+c,顶点坐标 当时,函数达到最大值(a<0)或最小值(a>0): 学生先发言总结,在教师的引导下总结归纳本节二次函数的一般式内容。 让学生自己对本节课知识进行整合归纳,培养学生养成及时总结的习惯。
板书 课题:1.2二次函数的图像与性质(5)1.画二次函数y=ax +bx+c的步骤:列表、描点、连线2.二次函数y=ax +bx+c的图像与性质顶点坐标最值
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
