26.2 等可能情形下的概率计算(3) 课件(共25张PPT)
文档属性
| 名称 | 26.2 等可能情形下的概率计算(3) 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 953.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-21 17:55:23 | ||
图片预览







文档简介
(共25张PPT)
沪科版 九年级下册
26.2等可能情形下的概率计算(3)
本课是在学生已经学习了用列表法求概率的基础上,继续用画树状图法求概率,深化学生对用列举法求概率的认识.
课件说明
教学目标:
用画树状图法求事件的概率.
教学重点:
用画树状图法求事件的概率.
在一次试验中,如果可能出现的结果只有有限个,且各种结果出现的可能性大小相等,那么我们可以通过列举试验结果的方法,求出随机事件发生的概率,这种求概率的方法叫列举法.
复习旧知
1.一个口袋中有四个完全相同的小球,把它们分别标号为1、2、3、4,随机地摸出一个小球,然后放回,再随机地摸出一个小球,则两次摸出的小球标号的和等于4的概率是 .
1
4
2.把4个完全相同的乒乓球标上数字2,3,4,5,然后放到一个不透明的口袋中,第一次任意摸出一个球(不放回),第二次再任意摸出一个球. 则两次摸出的球所标数字之和是7的概率是 .
1
3
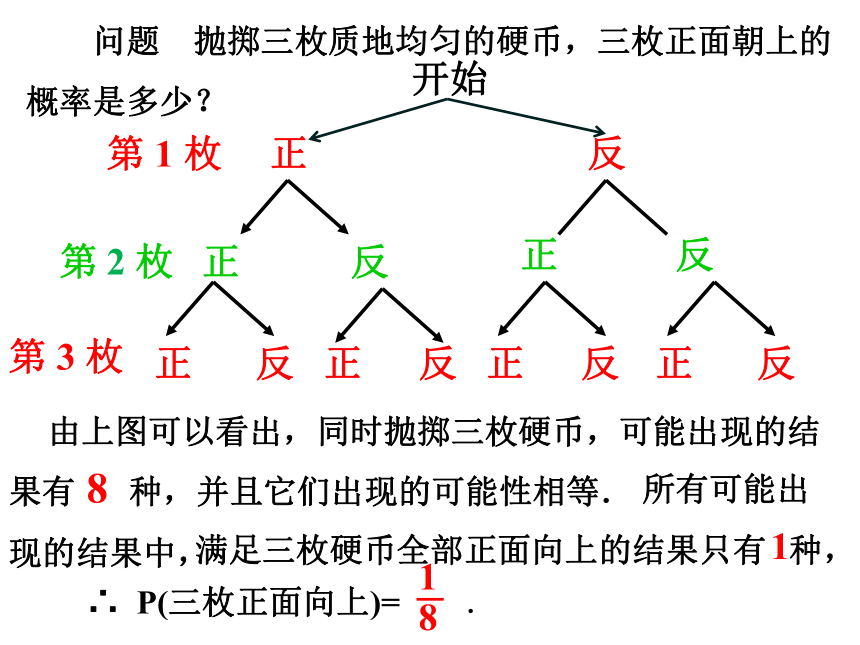
问题 抛掷三枚质地均匀的硬币,三枚正面朝上的概率是多少?
第 1 枚
正
反
第 2 枚
正
反
反
正
正
反
正
反
正
反
正
反
第 3 枚
由上图可以看出,同时抛掷三枚硬币,可能出现的结果有 种,并且它们出现的可能性相等.
现的结果中,
所有可能出
满足三枚硬币全部正面向上的结果只有 种,
∴ P(三枚正面向上)= .
8
1
开始
1
8
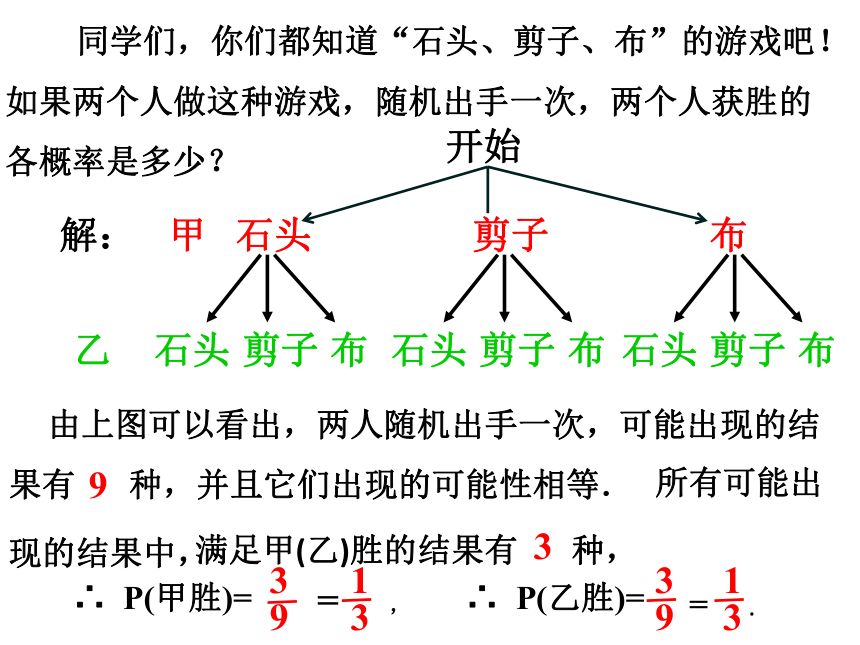
同学们,你们都知道“石头、剪子、布”的游戏吧!如果两个人做这种游戏,随机出手一次,两个人获胜的各概率是多少?
解:
甲
石头
乙
石头
剪子
布
由上图可以看出,两人随机出手一次,可能出现的结果有 种,并且它们出现的可能性相等.
现的结果中,
所有可能出
满足甲(乙)胜的结果有 种,
∴ P(甲胜)=
= ,
∴ P(乙胜)=
3
9
= .
1
3
剪子
石头
剪子
布
布
石头
剪子
布
9
3
开始
3
9
1
3
用列表法和树形图法求概率时应注意什么情况?
利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果;从而较方便地求出某些事件发生的概率.当试验包含两步时,列表法比较方便,当然,此时也可以用树状图法,当试验在三步或三步以上时,用树状图法方便.
例6 某人的密码箱的密码由三个数字组成,每个数字都是从0~9的10个数字中任选的.如果他忘记了自己设定的密码,求在一次随机试验中他能打开箱子的概率.
设在一次随机试验中他能打开箱子的事件为A.
解:
根据题意,在一次随机试验中选择的号码应是000~999中的任意一个3位数,所有可能出现的结果共有1000种,且出现每一种结果的可能性相等.要打开箱子,即选择的号码与密码相同的结果只有1种,
∴ P(A)=
1
1000
在一次随机试验中他能打开箱子的概率为 .
答:
1
1000
例7 甲、乙两人要去风景区游玩,仅知道每天开往风景区有3辆车,并且舒适程度分为上、中、下等3种,而不知道怎样区分这些车,也不知道它们会以怎样的顺序开来.于是他们分别采取了不同的乘车方法;甲乘第1辆开来的车,乙不乘第1辆车并且仔细观察第2辆车的情况:如比第1辆好,就乘第2辆车,如不比第1辆车好就乘第3辆车.试问甲、乙两人的乘车办法,哪一种更有利于乘上舒适度较好的车?
开始
上
中
下
中
下
解:
用树状图来表示上述所有可能出现的结果
第1辆
上
下
下
上
上
中
中
上
第2辆
三辆汽车开来的先后顺序有6中情况,
假定六种顺序出现的可能性相等,
甲乘到上等、中等、下等三种汽车的概率都是 = ;
第3辆
下
中
2
6
1
3
开始
上
中
下
中
下
下
中
解:
用树状图来表示上述所有可能出现的结果
上
下
下
上
上
中
中
上
而乙乘到上等车的概率是 = ;乘中等车的概率是 = ;
因而,按乙的办法乘上舒适度较好的车的可能性更大.
第1辆
第2辆
第3辆
3
6
1
2
2
6
1
3
乘下等车的概率是 ;
1
6
顺序 甲 乙
解:
用列表法来表示上述所有可能出现的结果
三辆汽车开来的先后顺序有6中情况,
假定六种顺序出现的可能性相等,
甲乘到上等、中等、下等三种汽车的概率都是 = ;
2
6
1
3
上
上
中
中
下
下
(上中下)
(上下中)
(中上下)
(中下上)
(下上中)
(下中上)
顺序 甲 乙
(上中下) 上
(上下中) 上
(中上下) 中
(中下上) 中
(下上中) 下
(下中上) 下
解:
用列表法来表示上述所有可能出现的结果
而乙乘到上等车的概率是 ;乘中等车的概率是 ;
∴按乙的办法乘上舒适度较好的车的可能性更大.
1
2
1
3
乘下等车的概率是 ;
1
6
下
中
上
上
上
中
2.密码锁的密码是一个五位数字的号码,每位
上的数字都是0到9中的任一个.在开锁时,某人
忘了密码最后两个数字,他随意拨动最后两位
号码,恰好打开锁的概率是多少?
解:
设在一次随机试验中他能打开锁的事件为A.
根据题意,密码最后两个数字应是00~99中的任意一个2位数,所有可能出现的结果共有100种,且出现每一种结果的可能性相等.要打开箱子,即选择的号码与密码相同的结果只有1种,
∴ P(A)=
1
100
3.元旦联欢会上,小明设计了一种翻牌游戏:先在9张大小
相同的正方形纸牌上分别写上数字1,2,3,…,9;再
在另一面写上奖品的名称,其中4张写的是“铅笔”,
3张写的是“贺年卡”,2张写的是“笔记本”.如图,
将9张纸牌贴在黑板上.
(1)小丽第一个翻牌请问她获得奖品,
“笔记本”的概率是多少?
(2)若小丽翻到的是“贺年卡” ,则第二个翻牌人
小勇翻到“铅笔”的概率是多少?
1
2
3
4
5
6
7
8
9
3.元旦联欢会上,小明设计了一种翻牌游戏:先在9张大小
相同的正方形纸牌上分别写上数字1,2,3,…,9;再
在另一面写上奖品的名称,其中4张写的是“铅笔”,
3张写的是“贺年卡”,2张写的是“笔记本”.如图,
将9张纸牌贴在黑板上.
(1)小丽第一个翻牌,请问她获得奖品
“笔记本”的概率是多少?
∵随机翻牌一次,可能出现的结果
有 种,
获得“笔记本”的结果有 种,
∴ P(笔记本)=
2
9
解:(1)
9
2
1
2
3
4
5
6
7
8
9
3.元旦联欢会上,小明设计了一种翻牌游戏:先在9张大小相同的正方形纸牌上分别写上数字1,2,3,…,9;再在另一面写上奖品的名称,其中4张写的是“铅笔”,3张写的是“贺年卡”,2张写的是“笔记本”.如图,将9张纸牌贴在黑板上.
(2)若小丽翻到的是“贺年卡” ,
则第二个翻牌人小勇翻到
“铅笔”的概率是多少?
∵第二个翻牌人随机翻牌一次,可能出现的
结果有 种,
∴ P(铅笔)=
4
8
(2)
8
获得“铅笔”的结果有 种,
4
= .
1
2
1
2
3
4
5
6
7
8
9
(1)画树状图法求概率的一般步骤是什么?
(2)相对列表法,画树状图法在列举试验所有等
可能结果方面有什么优势?
课堂小结
1.学校新开设了国画、彩绘、泥塑三个社团,如果小李、小张两名同学每人随机选择参加其中一个社团,那么小李和小张选到同一社团的概率为 ( ) .
A. B. C. D.
2
3
1
2
1
3
1
4
巩固新知
C
2.三张背面完全相同的数字牌,它们的正面分别印有数字“3”、“4”、“5”,将它们背面朝上,洗匀后随机抽取一张,记录牌上的数字并把牌放回,再重复这样的步骤两次,得到三个数字
3、4、5,则以3、4、5为边长正好构成等边三角形的概率是( ).
A. B. C. D.
1
9
1
27
5
9
1
3
A
3.把4个完全相同的乒乓球标上数字2,3,4,5,然后放到一个不透明的口袋中,第一次任意摸出一个球(不放回),第二次再任意摸出一个球. (1)请补充完整下面的树形图.
(2)根据树形图可知,两次摸出的球所标数字之和是7的概率是 .
开始
第一次
2
3
5
4
5
9
4
9
第二次
两数之和为
2
6
2
7
5
6
4
4
2
5
7
8
8
3
3
5
5
7
3
7
1
3
4. 某电脑店有A、B两种型号的打印机和C、D、E三种芯片出售.每种型号的打印机均需要一种芯片配套才能打印.
(1)下列是该店用树形图或列表设计的配套方案,
①的位置应填写____,②的位置应填写_____ ;
(2)若仅有B型打印机与E种芯片不配套,则上面
(1)中的方案配套成功率是____.
芯片 打印机 C D E
A (A,C) (A,D) ②
B (B,C) (B,D) (B,E)
配套
方案
A
C
D
E
B
C
D
①
E
(A,E)
5
6
今天作业
课本P116页第7、8题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级下册
26.2等可能情形下的概率计算(3)
本课是在学生已经学习了用列表法求概率的基础上,继续用画树状图法求概率,深化学生对用列举法求概率的认识.
课件说明
教学目标:
用画树状图法求事件的概率.
教学重点:
用画树状图法求事件的概率.
在一次试验中,如果可能出现的结果只有有限个,且各种结果出现的可能性大小相等,那么我们可以通过列举试验结果的方法,求出随机事件发生的概率,这种求概率的方法叫列举法.
复习旧知
1.一个口袋中有四个完全相同的小球,把它们分别标号为1、2、3、4,随机地摸出一个小球,然后放回,再随机地摸出一个小球,则两次摸出的小球标号的和等于4的概率是 .
1
4
2.把4个完全相同的乒乓球标上数字2,3,4,5,然后放到一个不透明的口袋中,第一次任意摸出一个球(不放回),第二次再任意摸出一个球. 则两次摸出的球所标数字之和是7的概率是 .
1
3
问题 抛掷三枚质地均匀的硬币,三枚正面朝上的概率是多少?
第 1 枚
正
反
第 2 枚
正
反
反
正
正
反
正
反
正
反
正
反
第 3 枚
由上图可以看出,同时抛掷三枚硬币,可能出现的结果有 种,并且它们出现的可能性相等.
现的结果中,
所有可能出
满足三枚硬币全部正面向上的结果只有 种,
∴ P(三枚正面向上)= .
8
1
开始
1
8
同学们,你们都知道“石头、剪子、布”的游戏吧!如果两个人做这种游戏,随机出手一次,两个人获胜的各概率是多少?
解:
甲
石头
乙
石头
剪子
布
由上图可以看出,两人随机出手一次,可能出现的结果有 种,并且它们出现的可能性相等.
现的结果中,
所有可能出
满足甲(乙)胜的结果有 种,
∴ P(甲胜)=
= ,
∴ P(乙胜)=
3
9
= .
1
3
剪子
石头
剪子
布
布
石头
剪子
布
9
3
开始
3
9
1
3
用列表法和树形图法求概率时应注意什么情况?
利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果;从而较方便地求出某些事件发生的概率.当试验包含两步时,列表法比较方便,当然,此时也可以用树状图法,当试验在三步或三步以上时,用树状图法方便.
例6 某人的密码箱的密码由三个数字组成,每个数字都是从0~9的10个数字中任选的.如果他忘记了自己设定的密码,求在一次随机试验中他能打开箱子的概率.
设在一次随机试验中他能打开箱子的事件为A.
解:
根据题意,在一次随机试验中选择的号码应是000~999中的任意一个3位数,所有可能出现的结果共有1000种,且出现每一种结果的可能性相等.要打开箱子,即选择的号码与密码相同的结果只有1种,
∴ P(A)=
1
1000
在一次随机试验中他能打开箱子的概率为 .
答:
1
1000
例7 甲、乙两人要去风景区游玩,仅知道每天开往风景区有3辆车,并且舒适程度分为上、中、下等3种,而不知道怎样区分这些车,也不知道它们会以怎样的顺序开来.于是他们分别采取了不同的乘车方法;甲乘第1辆开来的车,乙不乘第1辆车并且仔细观察第2辆车的情况:如比第1辆好,就乘第2辆车,如不比第1辆车好就乘第3辆车.试问甲、乙两人的乘车办法,哪一种更有利于乘上舒适度较好的车?
开始
上
中
下
中
下
解:
用树状图来表示上述所有可能出现的结果
第1辆
上
下
下
上
上
中
中
上
第2辆
三辆汽车开来的先后顺序有6中情况,
假定六种顺序出现的可能性相等,
甲乘到上等、中等、下等三种汽车的概率都是 = ;
第3辆
下
中
2
6
1
3
开始
上
中
下
中
下
下
中
解:
用树状图来表示上述所有可能出现的结果
上
下
下
上
上
中
中
上
而乙乘到上等车的概率是 = ;乘中等车的概率是 = ;
因而,按乙的办法乘上舒适度较好的车的可能性更大.
第1辆
第2辆
第3辆
3
6
1
2
2
6
1
3
乘下等车的概率是 ;
1
6
顺序 甲 乙
解:
用列表法来表示上述所有可能出现的结果
三辆汽车开来的先后顺序有6中情况,
假定六种顺序出现的可能性相等,
甲乘到上等、中等、下等三种汽车的概率都是 = ;
2
6
1
3
上
上
中
中
下
下
(上中下)
(上下中)
(中上下)
(中下上)
(下上中)
(下中上)
顺序 甲 乙
(上中下) 上
(上下中) 上
(中上下) 中
(中下上) 中
(下上中) 下
(下中上) 下
解:
用列表法来表示上述所有可能出现的结果
而乙乘到上等车的概率是 ;乘中等车的概率是 ;
∴按乙的办法乘上舒适度较好的车的可能性更大.
1
2
1
3
乘下等车的概率是 ;
1
6
下
中
上
上
上
中
2.密码锁的密码是一个五位数字的号码,每位
上的数字都是0到9中的任一个.在开锁时,某人
忘了密码最后两个数字,他随意拨动最后两位
号码,恰好打开锁的概率是多少?
解:
设在一次随机试验中他能打开锁的事件为A.
根据题意,密码最后两个数字应是00~99中的任意一个2位数,所有可能出现的结果共有100种,且出现每一种结果的可能性相等.要打开箱子,即选择的号码与密码相同的结果只有1种,
∴ P(A)=
1
100
3.元旦联欢会上,小明设计了一种翻牌游戏:先在9张大小
相同的正方形纸牌上分别写上数字1,2,3,…,9;再
在另一面写上奖品的名称,其中4张写的是“铅笔”,
3张写的是“贺年卡”,2张写的是“笔记本”.如图,
将9张纸牌贴在黑板上.
(1)小丽第一个翻牌请问她获得奖品,
“笔记本”的概率是多少?
(2)若小丽翻到的是“贺年卡” ,则第二个翻牌人
小勇翻到“铅笔”的概率是多少?
1
2
3
4
5
6
7
8
9
3.元旦联欢会上,小明设计了一种翻牌游戏:先在9张大小
相同的正方形纸牌上分别写上数字1,2,3,…,9;再
在另一面写上奖品的名称,其中4张写的是“铅笔”,
3张写的是“贺年卡”,2张写的是“笔记本”.如图,
将9张纸牌贴在黑板上.
(1)小丽第一个翻牌,请问她获得奖品
“笔记本”的概率是多少?
∵随机翻牌一次,可能出现的结果
有 种,
获得“笔记本”的结果有 种,
∴ P(笔记本)=
2
9
解:(1)
9
2
1
2
3
4
5
6
7
8
9
3.元旦联欢会上,小明设计了一种翻牌游戏:先在9张大小相同的正方形纸牌上分别写上数字1,2,3,…,9;再在另一面写上奖品的名称,其中4张写的是“铅笔”,3张写的是“贺年卡”,2张写的是“笔记本”.如图,将9张纸牌贴在黑板上.
(2)若小丽翻到的是“贺年卡” ,
则第二个翻牌人小勇翻到
“铅笔”的概率是多少?
∵第二个翻牌人随机翻牌一次,可能出现的
结果有 种,
∴ P(铅笔)=
4
8
(2)
8
获得“铅笔”的结果有 种,
4
= .
1
2
1
2
3
4
5
6
7
8
9
(1)画树状图法求概率的一般步骤是什么?
(2)相对列表法,画树状图法在列举试验所有等
可能结果方面有什么优势?
课堂小结
1.学校新开设了国画、彩绘、泥塑三个社团,如果小李、小张两名同学每人随机选择参加其中一个社团,那么小李和小张选到同一社团的概率为 ( ) .
A. B. C. D.
2
3
1
2
1
3
1
4
巩固新知
C
2.三张背面完全相同的数字牌,它们的正面分别印有数字“3”、“4”、“5”,将它们背面朝上,洗匀后随机抽取一张,记录牌上的数字并把牌放回,再重复这样的步骤两次,得到三个数字
3、4、5,则以3、4、5为边长正好构成等边三角形的概率是( ).
A. B. C. D.
1
9
1
27
5
9
1
3
A
3.把4个完全相同的乒乓球标上数字2,3,4,5,然后放到一个不透明的口袋中,第一次任意摸出一个球(不放回),第二次再任意摸出一个球. (1)请补充完整下面的树形图.
(2)根据树形图可知,两次摸出的球所标数字之和是7的概率是 .
开始
第一次
2
3
5
4
5
9
4
9
第二次
两数之和为
2
6
2
7
5
6
4
4
2
5
7
8
8
3
3
5
5
7
3
7
1
3
4. 某电脑店有A、B两种型号的打印机和C、D、E三种芯片出售.每种型号的打印机均需要一种芯片配套才能打印.
(1)下列是该店用树形图或列表设计的配套方案,
①的位置应填写____,②的位置应填写_____ ;
(2)若仅有B型打印机与E种芯片不配套,则上面
(1)中的方案配套成功率是____.
芯片 打印机 C D E
A (A,C) (A,D) ②
B (B,C) (B,D) (B,E)
配套
方案
A
C
D
E
B
C
D
①
E
(A,E)
5
6
今天作业
课本P116页第7、8题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
