7.3万有引力理论的成就 人教版(2019)必修二高中物理精品课件(共17张PPT)
文档属性
| 名称 | 7.3万有引力理论的成就 人教版(2019)必修二高中物理精品课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 11.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-12-21 17:35:52 | ||
图片预览





文档简介
(共17张PPT)
必修二第七章
7.3万有引力理论的成就
思考:我们经常用各种秤来测量物体的质量,那么我们能否测量天体的质量呢?
新课引入
已知
条件:适用于两个质点或者两个匀质球体之间
其中
a.对于两个质点,r指两个质点之间的距离
b.对于两个匀质球体,r指两球心之间的距离
注意:
当两物体距离r趋于为零时,F万并不是趋于无穷大
因为r趋于0时,万有引力公式不在适用。
R
F
m
M
忽略自转
天体质量计算
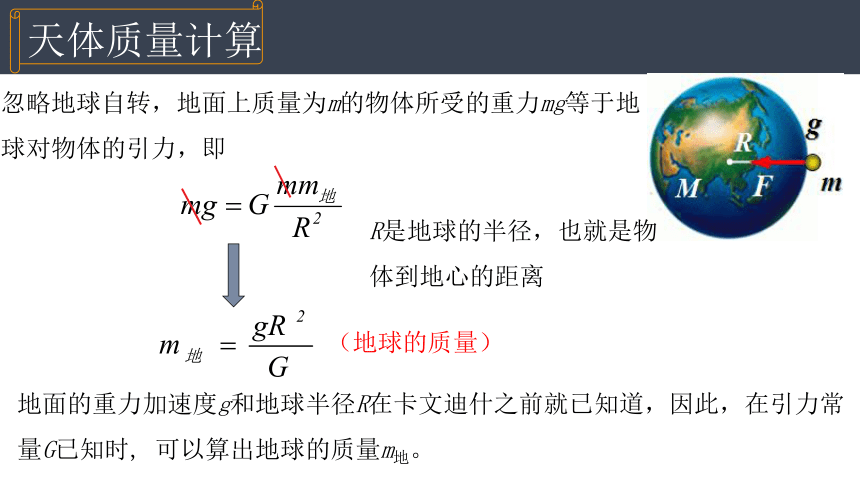
忽略地球自转,地面上质量为m的物体所受的重力mg等于地球对物体的引力,即
(地球的质量)
R是地球的半径,也就是物体到地心的距离
地面的重力加速度g和地球半径R在卡文迪什之前就已知道,因此,在引力常量G已知时, 可以算出地球的质量m地。
天体质量计算
地球的质量:
引力常量: G= 6.67×10-11Nm2/kg2
m地= 6.0×1024kg
地表重力加速度: g = 9.8m/s2
地球半径: R = 6400km
60万亿亿吨
天体质量计算
①在星球表面任选一物体m作为研究对象
②忽略星球自转影响,重力等于其所受的万有引力
g指星球表面重力加速度;R指星球半径。
天体质量计算
F
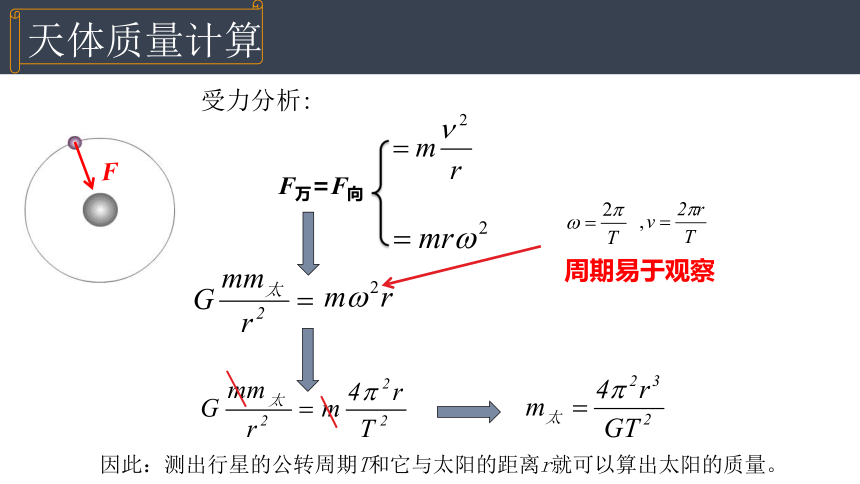
受力分析:
周期易于观察
F万=F向
因此:测出行星的公转周期T和它与太阳的距离r就可以算出太阳的质量。
天体质量计算
已知太阳与地球间的平均距离约为1.5×1011m,你能估算太阳的质量吗?
引力常量: G= 6.67×10-11Nm2/kg2
m太= 2×1030kg
轨道半径: r = 1.5×1011m
地球公转周期:T = 1年=31536000s
是地球质量的33万倍
天体质量计算
思考:换用其他行星的相关数据进行估算,结果会相近吗?为什么?
开普勒第三定律
=k
只与中心天体质量m有关
因此:结果相同
天体质量计算
环绕法测量天体质量
T指环绕周期,r指环绕半径。
F万=F向
天体质量计算
2.环绕法:环绕天体所需向心力由中心天体对环绕天体的万有引力提供
1.表面法:地面(星球表面)的物体的重力近似等于万有引力
只能求出中心天体的质量
课堂小结
发现未知天体
笔尖下发现的行星——海王星
其它成就
预言哈雷彗星回归
解释自然现象
典型例题
例1. 2022年2月27日,我国以“1箭22星”方式成功将22颗卫星发射升空。其中某颗卫星运行的圆轨道离地高为h,周期为T。已知地球半径为R,引力常量为G,根据上述数据,可以计算出的物理量有( )
A.地球的质量 B.地球表面的重力加速度
C.地球对卫星的万有引力 D.卫星运行时的动能
AB
典型例题
典型例题
例3. “嫦娥一号”的成功发射,为实现中华民族几千年的奔月梦想迈出了重要的一步。已知“嫦娥一号”绕月飞行轨道近似为圆形,距月球表面高度为,飞行周期为,月球的半径为,引力常量为。求:
(1)“嫦娥一号”绕月飞行时的线速度大小;
(2)月球的质量;
(3)若发射一颗绕月球表面做匀速圆周运动的飞船,则其绕月运行的线速度应为多大.
典型例题
例4.为了探知未知天体,假如宇航员乘坐宇宙飞船到达某星球,测得飞船在该星球表面附近做圆周运动的周期为。飞船降落到该星球表面后,宇航员将小球从高处以初速度水平抛出,落地时水平位移为,忽略空气阻力和该星球的自转,已知引力常量为,将该星球视为质量分布均匀的球体,则以下说法正确的是( )
A.该星球的半径为 B.该星球的半径为
C.该星球的质量为 D.该星球的质量为
AC
感谢您的观看
必修二第七章
7.3万有引力理论的成就
思考:我们经常用各种秤来测量物体的质量,那么我们能否测量天体的质量呢?
新课引入
已知
条件:适用于两个质点或者两个匀质球体之间
其中
a.对于两个质点,r指两个质点之间的距离
b.对于两个匀质球体,r指两球心之间的距离
注意:
当两物体距离r趋于为零时,F万并不是趋于无穷大
因为r趋于0时,万有引力公式不在适用。
R
F
m
M
忽略自转
天体质量计算
忽略地球自转,地面上质量为m的物体所受的重力mg等于地球对物体的引力,即
(地球的质量)
R是地球的半径,也就是物体到地心的距离
地面的重力加速度g和地球半径R在卡文迪什之前就已知道,因此,在引力常量G已知时, 可以算出地球的质量m地。
天体质量计算
地球的质量:
引力常量: G= 6.67×10-11Nm2/kg2
m地= 6.0×1024kg
地表重力加速度: g = 9.8m/s2
地球半径: R = 6400km
60万亿亿吨
天体质量计算
①在星球表面任选一物体m作为研究对象
②忽略星球自转影响,重力等于其所受的万有引力
g指星球表面重力加速度;R指星球半径。
天体质量计算
F
受力分析:
周期易于观察
F万=F向
因此:测出行星的公转周期T和它与太阳的距离r就可以算出太阳的质量。
天体质量计算
已知太阳与地球间的平均距离约为1.5×1011m,你能估算太阳的质量吗?
引力常量: G= 6.67×10-11Nm2/kg2
m太= 2×1030kg
轨道半径: r = 1.5×1011m
地球公转周期:T = 1年=31536000s
是地球质量的33万倍
天体质量计算
思考:换用其他行星的相关数据进行估算,结果会相近吗?为什么?
开普勒第三定律
=k
只与中心天体质量m有关
因此:结果相同
天体质量计算
环绕法测量天体质量
T指环绕周期,r指环绕半径。
F万=F向
天体质量计算
2.环绕法:环绕天体所需向心力由中心天体对环绕天体的万有引力提供
1.表面法:地面(星球表面)的物体的重力近似等于万有引力
只能求出中心天体的质量
课堂小结
发现未知天体
笔尖下发现的行星——海王星
其它成就
预言哈雷彗星回归
解释自然现象
典型例题
例1. 2022年2月27日,我国以“1箭22星”方式成功将22颗卫星发射升空。其中某颗卫星运行的圆轨道离地高为h,周期为T。已知地球半径为R,引力常量为G,根据上述数据,可以计算出的物理量有( )
A.地球的质量 B.地球表面的重力加速度
C.地球对卫星的万有引力 D.卫星运行时的动能
AB
典型例题
典型例题
例3. “嫦娥一号”的成功发射,为实现中华民族几千年的奔月梦想迈出了重要的一步。已知“嫦娥一号”绕月飞行轨道近似为圆形,距月球表面高度为,飞行周期为,月球的半径为,引力常量为。求:
(1)“嫦娥一号”绕月飞行时的线速度大小;
(2)月球的质量;
(3)若发射一颗绕月球表面做匀速圆周运动的飞船,则其绕月运行的线速度应为多大.
典型例题
例4.为了探知未知天体,假如宇航员乘坐宇宙飞船到达某星球,测得飞船在该星球表面附近做圆周运动的周期为。飞船降落到该星球表面后,宇航员将小球从高处以初速度水平抛出,落地时水平位移为,忽略空气阻力和该星球的自转,已知引力常量为,将该星球视为质量分布均匀的球体,则以下说法正确的是( )
A.该星球的半径为 B.该星球的半径为
C.该星球的质量为 D.该星球的质量为
AC
感谢您的观看
