图形的旋转和中心对称(中考复习)[下学期]
文档属性
| 名称 | 图形的旋转和中心对称(中考复习)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 627.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-09-25 15:51:00 | ||
图片预览






文档简介
课件16张PPT。二、空间与图形 图形的旋转和中心对称目录一、中考目标图形的旋转
通过具体实例认识旋转 a
探索旋转的基本性质、理解对应点到旋转中心的距离相等、对应点与旋转中心连线所成的角度彼此相等的性质 c
了解平行四边形、圆是中心对称图形 a
能作出简单平面图形旋转后的图形 c
探索图形之间的变换关系(轴对称、平移、旋转及其组合) c
灵活运用轴对称、平移、旋转及其组合进行图案设计 c
认识旋转在现实生活中的应用 c
二、知识概要1.概念:
旋转:如果一个图形绕某一个定点沿某一个方向转动一个角度,这样的图形运动称为旋转.这个定点称为旋转中心,转动的角度称为旋转角.
中心对称图形:图形绕着中心旋转180°后与自身重合称中心对称图形(如:平行四边形、圆等)。二、知识概要2.性质:
旋转不改变图形的形状和大小(即旋转前后的两个图形全等).
任意一对对应点与旋转中心的连线所成的角彼此相等(都是旋转角).
经过旋转,对应点到旋转中心的距离相等.
3.旋转三要点:旋转①中心,②方向,③角度.
4.对称、平移、旋转及其组合
灵活运用轴对称、中心对称、平移和旋转的组合进行图案设计.
按要求作出简单平面图形变换后的图形.
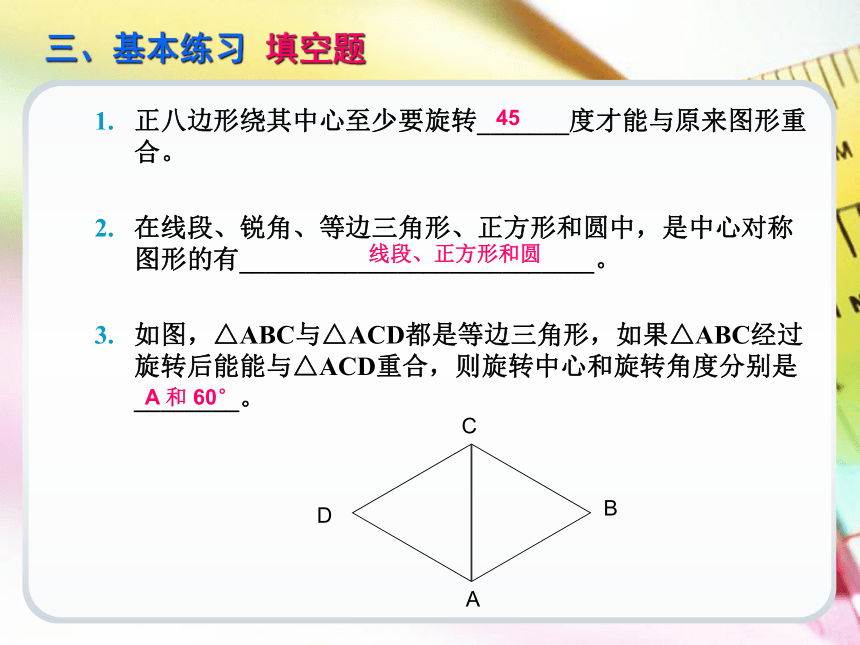
正八边形绕其中心至少要旋转_______度才能与原来图形重合。
在线段、锐角、等边三角形、正方形和圆中,是中心对称图形的有___________________________。
如图,△ABC与△ACD都是等边三角形,如果△ABC经过旋转后能能与△ACD重合,则旋转中心和旋转角度分别是________。三、基本练习 填空题45A 和 60°线段、正方形和圆三、基本练习 选择题若两个图形关于某一点成中心对称,那么下列说法:
对称点的连线必过对称中心;
这两个图形一定全等;
对应线段一定平行且相等;
将一个图形绕对称中心旋转180°必定与另一个图形重合。
其中正确的是( )。
(A) ①② (B) ①③ (C) ①②③ (D) ①②③④
如图,如果正方形CDEF旋转后能与正 方形ABCD重合,那么图形所在的平面 上可以作为旋转中心的点共有( )。
(A) 4 (B) 3 (C) 2 (D) 1CB
如图,△ABC是等边三角形。D是BC上一点,△ABD经过旋转后到达△ACE的位置。
旋转中心是哪一点
旋转了多少度?
如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
四、范例精析
下图是某设计师设计的方桌边图案的一部分。请你运用旋转变换的方法,在坐标纸上将该图形绕原点顺时针依次旋转90°,180°,270°,并画出它在各象限内的图形。
四、范例精析四、范例精析如图甲,正方形ABCD和正方形CEFG共一顶点C,且B,C,E在一条直线上。连接BG,DE.
请你猜测BG,DE的位置关系和数量关系,并说明理由;
若正方形CEFG绕C点顺时针方向旋转一个角度后,如图乙,BG和DE是否还有上述关系?是说明理由。
四、范例精析一张餐桌如图,餐桌的中心已经放上一个圆形的火锅。一个游戏规则是:两人轮流沿桌面四周摆放同样大小的茶碗,每人每次摆放一个,茶碗不能互相重叠,谁先摆不下茶碗,就算谁输。你有没有必胜策略?四、范例精析在平面直角坐标系中,已知点P0的坐标为(1,0),将点P0绕着原点O按逆时针方向旋转30°得到点P1,延长OP1到点P2使O P2=2OP1;再将点P2绕原点O按逆时针方向旋转30°得到点P3,延长OP3到点P4使O P4=2OP3;……如此继续下去。求:
点P2的坐标;
点P2003的坐标.
四、范例精析(1)操作与说明:如图,O是边长为a的正方形ABCD的中心,将一块半径足够长,圆心角为直角的扇形纸板的圆心放在O点处,并将纸板绕O点旋转。则ABCD的边被纸板覆盖部分的总长度为定值a.试说明理由;四、范例精析( 接上页)
(2)尝试与思考:如图,将一块半径足够长的扇形纸板的圆心放在边长为a的正三角形的中心点O点处,并将纸板绕O点旋转,当扇形纸板的圆心角为_____时,正三角形的边被纸板覆盖部分的总长为定值a;当扇形纸板的圆心角为______时,正五边形的边被纸板覆盖部分的总长也为定值a;四、范例精析( 接上页)
(3)探究与引申:一般地,将一块半径足够长的扇形纸板的圆心放在边长为a的正n边形中心点O点处,并将纸板绕O点旋转,当扇形纸板的圆心角为_____时,正n边形的边被纸板覆盖部分的总长为定值a;这时正n边形被纸板覆盖部分的面积是否也为定值?若为定值,写出它与正n边形面积S之间的关系(不需说明理由);若不是定值,请说明理由。
结 束
通过具体实例认识旋转 a
探索旋转的基本性质、理解对应点到旋转中心的距离相等、对应点与旋转中心连线所成的角度彼此相等的性质 c
了解平行四边形、圆是中心对称图形 a
能作出简单平面图形旋转后的图形 c
探索图形之间的变换关系(轴对称、平移、旋转及其组合) c
灵活运用轴对称、平移、旋转及其组合进行图案设计 c
认识旋转在现实生活中的应用 c
二、知识概要1.概念:
旋转:如果一个图形绕某一个定点沿某一个方向转动一个角度,这样的图形运动称为旋转.这个定点称为旋转中心,转动的角度称为旋转角.
中心对称图形:图形绕着中心旋转180°后与自身重合称中心对称图形(如:平行四边形、圆等)。二、知识概要2.性质:
旋转不改变图形的形状和大小(即旋转前后的两个图形全等).
任意一对对应点与旋转中心的连线所成的角彼此相等(都是旋转角).
经过旋转,对应点到旋转中心的距离相等.
3.旋转三要点:旋转①中心,②方向,③角度.
4.对称、平移、旋转及其组合
灵活运用轴对称、中心对称、平移和旋转的组合进行图案设计.
按要求作出简单平面图形变换后的图形.
正八边形绕其中心至少要旋转_______度才能与原来图形重合。
在线段、锐角、等边三角形、正方形和圆中,是中心对称图形的有___________________________。
如图,△ABC与△ACD都是等边三角形,如果△ABC经过旋转后能能与△ACD重合,则旋转中心和旋转角度分别是________。三、基本练习 填空题45A 和 60°线段、正方形和圆三、基本练习 选择题若两个图形关于某一点成中心对称,那么下列说法:
对称点的连线必过对称中心;
这两个图形一定全等;
对应线段一定平行且相等;
将一个图形绕对称中心旋转180°必定与另一个图形重合。
其中正确的是( )。
(A) ①② (B) ①③ (C) ①②③ (D) ①②③④
如图,如果正方形CDEF旋转后能与正 方形ABCD重合,那么图形所在的平面 上可以作为旋转中心的点共有( )。
(A) 4 (B) 3 (C) 2 (D) 1CB
如图,△ABC是等边三角形。D是BC上一点,△ABD经过旋转后到达△ACE的位置。
旋转中心是哪一点
旋转了多少度?
如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
四、范例精析
下图是某设计师设计的方桌边图案的一部分。请你运用旋转变换的方法,在坐标纸上将该图形绕原点顺时针依次旋转90°,180°,270°,并画出它在各象限内的图形。
四、范例精析四、范例精析如图甲,正方形ABCD和正方形CEFG共一顶点C,且B,C,E在一条直线上。连接BG,DE.
请你猜测BG,DE的位置关系和数量关系,并说明理由;
若正方形CEFG绕C点顺时针方向旋转一个角度后,如图乙,BG和DE是否还有上述关系?是说明理由。
四、范例精析一张餐桌如图,餐桌的中心已经放上一个圆形的火锅。一个游戏规则是:两人轮流沿桌面四周摆放同样大小的茶碗,每人每次摆放一个,茶碗不能互相重叠,谁先摆不下茶碗,就算谁输。你有没有必胜策略?四、范例精析在平面直角坐标系中,已知点P0的坐标为(1,0),将点P0绕着原点O按逆时针方向旋转30°得到点P1,延长OP1到点P2使O P2=2OP1;再将点P2绕原点O按逆时针方向旋转30°得到点P3,延长OP3到点P4使O P4=2OP3;……如此继续下去。求:
点P2的坐标;
点P2003的坐标.
四、范例精析(1)操作与说明:如图,O是边长为a的正方形ABCD的中心,将一块半径足够长,圆心角为直角的扇形纸板的圆心放在O点处,并将纸板绕O点旋转。则ABCD的边被纸板覆盖部分的总长度为定值a.试说明理由;四、范例精析( 接上页)
(2)尝试与思考:如图,将一块半径足够长的扇形纸板的圆心放在边长为a的正三角形的中心点O点处,并将纸板绕O点旋转,当扇形纸板的圆心角为_____时,正三角形的边被纸板覆盖部分的总长为定值a;当扇形纸板的圆心角为______时,正五边形的边被纸板覆盖部分的总长也为定值a;四、范例精析( 接上页)
(3)探究与引申:一般地,将一块半径足够长的扇形纸板的圆心放在边长为a的正n边形中心点O点处,并将纸板绕O点旋转,当扇形纸板的圆心角为_____时,正n边形的边被纸板覆盖部分的总长为定值a;这时正n边形被纸板覆盖部分的面积是否也为定值?若为定值,写出它与正n边形面积S之间的关系(不需说明理由);若不是定值,请说明理由。
结 束
同课章节目录
