九年级数学上册 第二十三章旋转素养综合检测(含答案解析)
文档属性
| 名称 | 九年级数学上册 第二十三章旋转素养综合检测(含答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 580.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-21 19:33:05 | ||
图片预览



文档简介
第二十三章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共30分)
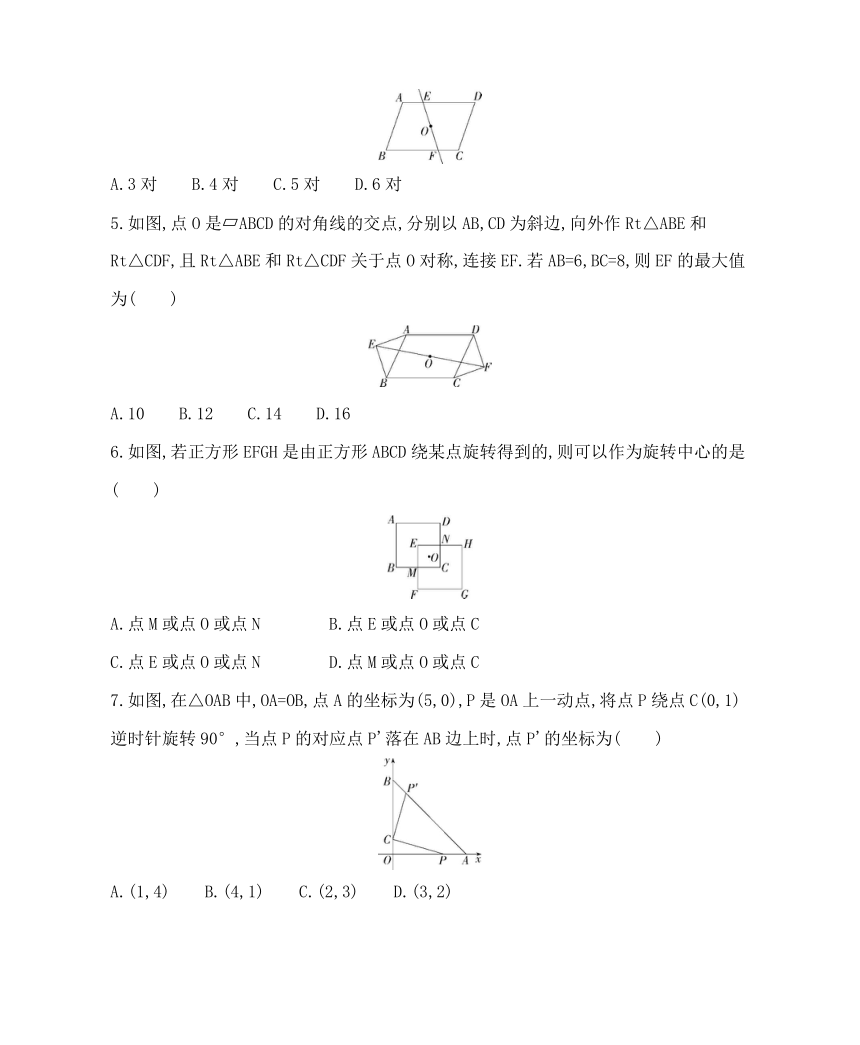
1.对称美是美的一种重要形式,它能给予人们一种圆满、协调的美感,下列图形属于中心对称图形的是( )
A B
C D
2.如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°,得到△AB'C'(点B的对应点是点B',点C的对应点是点C'),连接CC'.若∠CC'B'=32°,则∠ACB的度数是( )
A.13° B.15° C.32° D.77°
3.若a=-12 022,b=2 022-1,c=(-1)2 022, d=-2 022-1,则平面直角坐标系内的点A(a,b)与点A'(c,d)关于( )
A.y轴对称 B.x轴对称
C.原点对称 D.直线x=1对称
4.如图,四边形ABCD是中心对称图形,对称中心为点O,过点O的直线与AD、BC分别交于点E、F,则图中相等的线段有( )
A.3对 B.4对 C.5对 D.6对
5.如图,点O是 ABCD的对角线的交点,分别以AB,CD为斜边,向外作Rt△ABE和Rt△CDF,且Rt△ABE和Rt△CDF关于点O对称,连接EF.若AB=6,BC=8,则EF的最大值为( )
A.10 B.12 C.14 D.16
6.如图,若正方形EFGH是由正方形ABCD绕某点旋转得到的,则可以作为旋转中心的是( )
A.点M或点O或点N B.点E或点O或点C
C.点E或点O或点N D.点M或点O或点C
7.如图,在△OAB中,OA=OB,点A的坐标为(5,0),P是OA上一动点,将点P绕点C(0,1)逆时针旋转90°,当点P的对应点P'落在AB边上时,点P'的坐标为( )
A.(1,4) B.(4,1) C.(2,3) D.(3,2)
8.如图,在等边△ABC中,D是边AC上一动点,连接BD,将△BCD绕点B逆时针旋转60°得到△BAE,连接ED,若BC=10,则△AED的周长的最小值是( )
A.10 B.10
C.10+5 D.20
9.如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标分别为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交y轴于点P,若△ABC与△A'B'C'关于点P成中心对称,则点A'的坐标为( )
A.(-4,-5) B.(-5,-4)
C.(-3,-4) D.(-4,-3)
10.如图,矩形ABCD的顶点A、B分别在x轴、y轴上,OA=OB=2,AD=4,将矩形ABCD绕点O顺时针旋转,每次旋转90°,则第2 022次旋转结束时,点C的坐标为( )
A.(6,4) B.(-6,4)
C.(4,-6) D.(-4,6)
二、填空题(每小题4分,共24分)
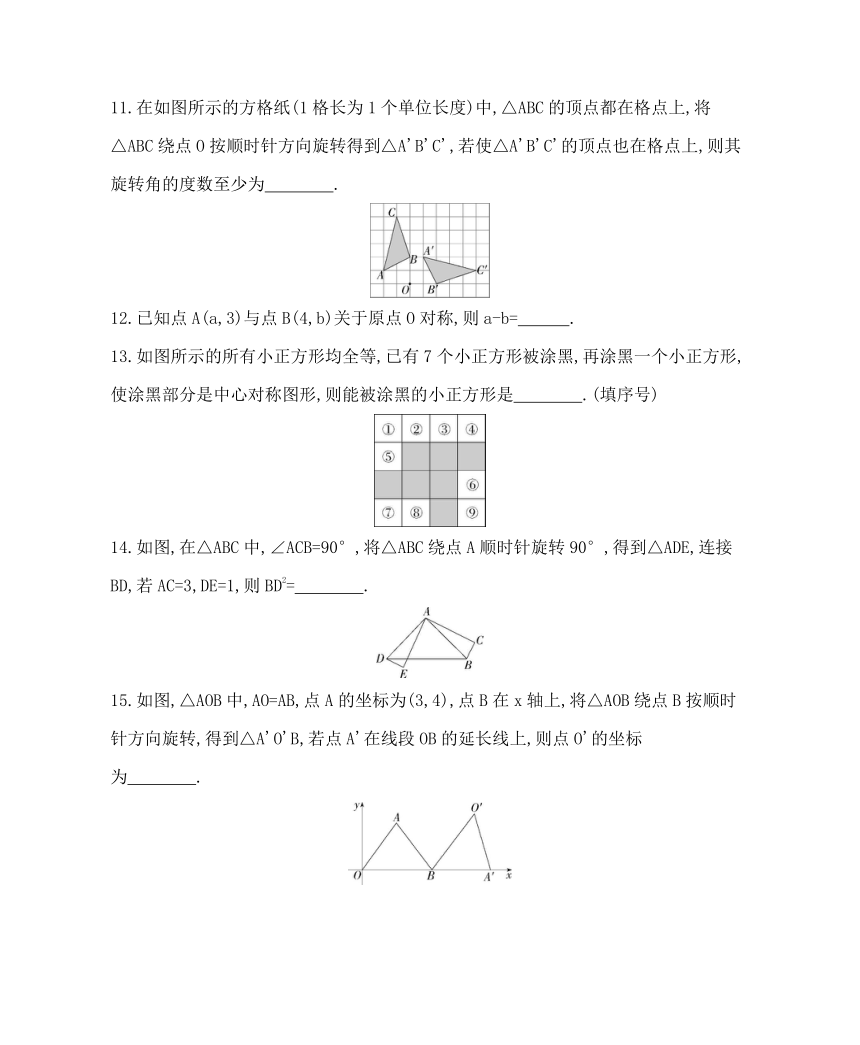
11.在如图所示的方格纸(1格长为1个单位长度)中,△ABC的顶点都在格点上,将△ABC绕点O按顺时针方向旋转得到△A'B'C',若使△A'B'C'的顶点也在格点上,则其旋转角的度数至少为 .
12.已知点A(a,3)与点B(4,b)关于原点O对称,则a-b= .
13.如图所示的所有小正方形均全等,已有7个小正方形被涂黑,再涂黑一个小正方形,使涂黑部分是中心对称图形,则能被涂黑的小正方形是 .(填序号)
14.如图,在△ABC中,∠ACB=90°,将△ABC绕点A顺时针旋转90°,得到△ADE,连接BD,若AC=3,DE=1,则BD2= .
15.如图,△AOB中,AO=AB,点A的坐标为(3,4),点B在x轴上,将△AOB绕点B按顺时针方向旋转,得到△A'O'B,若点A'在线段OB的延长线上,则点O'的坐标为 .
16.如图,P是等边三角形ABC内的一点,且PA=3,PB=4,PC=5,以BC为边在△ABC外作△BQC≌△BPA,连接PQ,则以下结论中正确是 .(填序号)
①△BPQ是等边三角形,②△BQC可看作由△BPA绕点B顺时针旋转60°得到,③△PCQ是直角三角形,④∠APB=150° ,⑤∠APC=120°.
三、解答题(共46分)
17.(8分)如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(5,4),B(0,3),C(2,1).
(1)画出△ABC关于原点中心对称的△A1B1C1,并写出点C1的坐标;
(2)画出将△A1B1C1绕点C1按顺时针方向旋转90°所得的△A2B2C1.
18.(8分)如图,在4×4的方格纸中,△ABC的三个顶点都在格点上.
(1)在图①中,画出一个与△ABC成中心对称的格点三角形;
(2)在图②中,画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形;
(3)在图③中,画出△ABC绕着点C按顺时针方向旋转90°后的三角形.
19.(10分)如图,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,将△ADF绕点A顺时针旋转90°,得到△ABG.
(1)求证:△EAG≌△EAF;
(2)若正方形ABCD的边长为6,DF=3,求BE的长.
20.(10分)如图,菱形ABCD有一个内角等于60°,将∠MAN的顶点与该菱形的顶点A重合,以点A为旋转中心,按顺时针方向旋转∠MAN,使它的两边分别交CB、DC于点E、F,已知∠MAN=60°.
(1)如图①,当BE=DF时,AE与AF的数量关系是 ;
(2)旋转∠MAN,如图②,当BE≠DF时,(1)中的结论是否还成立 若成立,加以证明;若不成立,请说明理由.
21.(10分)如图,已知△AOB和△MON都是等腰直角三角形,∠AOB=∠MON=90°.
(1)如图a,连接AM,BN,求证:△AOM≌△BON;
(2)若将△MON绕点O顺时针旋转,
①如图b,当点N恰好在AB边上时,求证:BN2+AN2=2ON2;
②当点A、M、N在同一条直线上时,若OB=4,ON=3,请直接写出线段BN的长.
答案全解全析
1.A 观察图形可知,选项A中图形绕圆心旋转180°后能与自身重合,是中心对称图形,其他图形只是轴对称图形.
2.A ∵将△ABC绕点A顺时针旋转90°,得到△AB'C',∴AC=AC',∠CAC'=90°,∠BCA=∠AC'B',∴△ACC'是等腰直角三角形,∴∠AC'C=45°,∴∠AC'B'=∠AC'C-∠CC'B'=45°-32°=13°,∴∠ACB=∠AC'B'=13°.
3.C ∵a=-12 022=-1,b=2 022-1=,c=(-1)2 022=1, d=-2 022-1=-,∴A与A'关于原点对称.
4.C 如图,连接AC、BD,∵四边形ABCD是中心对称图形,对称中心为点O,∴AC、BD的交点为点O,OA=OC,OB=OD,∴四边形ABCD是平行四边形,∴AB=CD,BC=AD,易知OE=OF,AE=CF,BF=DE,∴题图中相等的线段共有5对.故选C.
5.C 如图,取AB的中点G,连接EG,OG,AC.∵点O是 ABCD的对角线的交点,∴点O是AC的中点,∴OG是△ABC的中位线.∵BC=8,∴OG=BC=4.∵点G是Rt△ABE斜边AB的中点,AB=6,∴EG=AB=3.∵OE≤EG+OG=3+4=7,∴当点E、G、O在一条直线上时,OE有最大值,为7.又∵Rt△ABE和Rt△CDF关于点O对称,∴OE=OF,∴EF的最大值为2×7=14.
6.A 若以点M为旋转中心,把正方形ABCD顺时针旋转90°,则A点的对应点为H,B点的对应点为E,C点的对应点为F,D点的对应点为G,则可得到正方形EFGH;若以点O为旋转中心,把正方形ABCD旋转180°,则A点的对应点为G,B点的对应点为H,C点的对应点为E,D点的对应点为F,则可得到正方形EFGH;若以点N为旋转中心,把正方形ABCD逆时针旋转90°,则A点的对应点为F,B点的对应点为G,C点的对应点为H,D点的对应点为E,则可得到正方形EFGH.故选A.
A 如图,作P'H⊥BC于点H,∵将点P绕点C(0,1)逆时针旋转90°得点P',
∴PC=P'C,∠PCP'=90°,∴∠PCO+∠P'CH=90°.
∵∠PCO+∠OPC=90°,∴∠OPC=∠HCP',又∵∠COP=∠CHP',PC=P'C,
∴△OPC≌△HCP'(AAS),∴P'H=OC=1.∵OA=OB,∠AOB=90°,∴∠OBA=45°,∵P'H⊥BC,∴∠HP'B=45°,∴∠OBA=∠HP'B,∴BH=HP'=1,∴OH=OB-BH=4,∴P'(1,4).
C 如图,作BF⊥AC于点F,∵△ABC是等边三角形,BC=10,∴AC=10,AF=FC=5.在Rt△BFC中,BF===5.∵将△BCD绕点B逆时针旋转60°得到△BAE,∴BD=BE,∠DBE=60°,CD=AE,∴△DBE是等边三角形,∴BD=DE,∴△AED的周长=AE+AD+DE=CD+AD+BD=AC+BD,∴当BD最小,即BD=BF=5时,△AED的周长最小,最小值=AC+BF=10+5.故选C.
A 如图,过点A作AD⊥x轴于点D,交BC于点E,则AE⊥BC.∵点B,C的坐标分别为(2,1),(6,1),∴BC=6-2=4,DE=1,∵AB=AC,AE⊥BC,∴BE=EC=BC=2,∴OD=6-2=4,
∵∠BAC=90°,∴AE=BC=2,∴AD=AE+DE=3,∴A(4,3).设直线AB的解析式为y=kx+b(k≠0),∵直线AB经过A(4,3),B(2,1)两点,∴解得∴直线AB的解析式为y=x-1,当x=0时,y=-1,∴P(0,-1),∵△ABC与△A'B'C'关于点P成中心对称,∴点P为AA'的中点,设A'(x,y),则0=,-1=,解得x=-4,y=-5,
∴A'(-4,-5).故选A.
C 如图,作CE⊥y轴于点E,连接OC.
∵OA=OB=2,∴∠ABO=∠BAO=45°.∵∠ABC=90°,∴∠CBE=45°.∵BC=AD=4,∴CE=BE=4,∴OE=OB+BE=6,∴C(-4,6).∵矩形ABCD绕点O顺时针旋转,每次旋转90°,则第1次旋转结束时,点C的坐标为(6,4);第2次旋转结束时,点C的坐标为(4,-6);第3次旋转结束时,点C的坐标为(-6,-4);第4次旋转结束时,点C的坐标为(-4,6);……,发现规律:每旋转4次为一个循环,∵2 022÷4=505……2,∴第2 022次旋转结束时,点C的坐标为(4,-6).
11.90°
解析 如图,连接OB、OB',∠BOB'=90°,∴旋转角的度数至少为90°.
12.-1
解析 ∵点A(a,3)与点B(4,b)关于原点O对称,∴a=-4,b=-3,则a-b=-4-(-3)=-1.
13.②
解析 观察图形可知,要使涂黑部分是中心对称图形,只能涂黑②号小正方形.
14.20
解析 由题可知:BC=DE=1,AB=AD,∠BAD=90°,∵在Rt△ABC中,AC=3,BC=1,∠ACB=90°,∴AD=AB===,
∵∠BAD=90°,∴BD2=AB2+AD2=10+10=20.
15.
解析 如图,作AC⊥OB于点C,O'D⊥A'B于点D,∵A(3,4),∴OC=3,AC=4,由勾股定理,得OA==5.
∵OA=AB,AC⊥OB,∴OB=2OC=2×3=6.由旋转可知,△A'O'B≌△AOB,∴O'B=BO=6,A'B=AB=5,S△AOB=S△A'O'B,即OB·AC=A'B·O'D,∴O'D=.由勾股定理,得BD=,
∴OD=OB+BD=6+=,∴点O'的坐标为.
16.①②③④
解析 ①∵△ABC是等边三角形,∴∠ABC=60°,∵△BQC≌△BPA,∴∠CBQ=∠ABP,QB=PB=4,QC=PA=3,∠BQC=∠BPA,∴∠PBQ=∠PBC+∠CBQ=∠PBC+∠ABP=∠ABC=60°,∴△BPQ是等边三角形,所以①正确;②由△BQC≌△BPA和∠ABC=∠PBQ=60°可知△BQC可看作由△BPA绕点B顺时针旋转60°得到,故②正确;③∵△BPQ是等边三角形,
∴PQ=PB=4,∵PQ2+QC2=42+32=25,PC2=52=25,∴PQ2+QC2=PC2,∴∠PQC=90°,∴△PCQ是直角三角形,所以③正确;④∵△BPQ是等边三角形,
∴∠PQB=60°,∴∠APB=∠BQC=∠BQP+∠PQC=60°+90°=150°,所以④正确;
⑤∠APC=360°-150°-60°-∠QPC=150°-∠QPC,
∵∠PQC=90°,PC≠2QC,∴∠QPC≠30°,∴∠APC≠120°,所以⑤错误.所以正确的是①②③④.
17.解析 (1)△A1B1C1如图所示,点C1的坐标为(-2,-1).
(2)△A2B2C1如图所示.
18.解析 (1)答案不唯一,如:
(2)答案不唯一,如:
(3)如图,△A'B'C即为所求.
19.解析 (1)证明:∵将△ADF绕点A顺时针旋转90°得到△ABG,
∴△ADF≌△ABG,
∴AF=AG,∠DAF=∠BAG.
∵∠DAB=90°,∠EAF=45°,
∴∠DAF+∠EAB=45°,
∴∠BAG+∠EAB=45°,∴∠EAG=45°,
∴∠EAF=∠EAG.
在△EAG和△EAF中,
∴△EAG≌△EAF(SAS).
(2)由(1)知,△ABG≌△ADF,△EAF≌△EAG,∴BG=DF=3,EF=EG,
设BE=x,则EF=GE=3+x,CE=6-x,
∵CD=6,DF=3,∴CF=CD-DF=3,
∵∠C=90°,∴(6-x)2+32=(3+x)2,
解得x=2,即BE=2.
20.解析 (1)AE=AF.
理由:∵四边形ABCD是菱形,∴AB=AD,∠B=∠D.
在△ABE和△ADF中,
∴△ABE≌△ADF(SAS),∴AE=AF.
(2)仍然成立.
理由如下:如图,连接AC,
∵四边形ABCD是菱形,
∴AB=BC=AD=CD,又由题意知∠B=∠D=60°,
∴△ABC是等边三角形,△ACD是等边三角形,
∴AB=AC,∠ACD=∠B=∠BAC=60°,
∵∠MAN=60°,∴∠MAN=∠BAC,∴∠BAE+∠EAC=∠CAF+∠EAC,∴∠BAE=∠CAF.
在△BAE和△CAF中,
∴△BAE≌△CAF(ASA),∴AE=AF.
21.解析 (1)证明:∵∠AOB=∠MON=90°,
∴∠AOM=∠BON,
在△AOM和△BON中,
∴△AOM≌△BON(SAS).
(2)①证明:如图1,连接AM.
图1
同(1)可证△AOM≌△BON,∴AM=BN,∠OAM=∠B=45°.∵∠OAB=∠B=45°,
∴∠MAN=∠OAM+∠OAB=90°,∴在Rt△AMN中,MN2=AN2+AM2.
∵△MON是等腰直角三角形,∴MN2=2ON2,∴BN2+AN2=2ON2.
②BN=.
详解:分两种情况:如图2,过点O作OH⊥MN于点H.
图2
∵△AOM≌△BON,∴AM=BN,
∵OM=ON=3,∠MON=90°,OH⊥MN,
∴MN=3,MH=HN=OH=,
∴AH===,
∴BN=AM=MH+AH=.
如图3,同法可证BN=AM=.
图3
(满分100分,限时60分钟)
一、选择题(每小题3分,共30分)
1.对称美是美的一种重要形式,它能给予人们一种圆满、协调的美感,下列图形属于中心对称图形的是( )
A B
C D
2.如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°,得到△AB'C'(点B的对应点是点B',点C的对应点是点C'),连接CC'.若∠CC'B'=32°,则∠ACB的度数是( )
A.13° B.15° C.32° D.77°
3.若a=-12 022,b=2 022-1,c=(-1)2 022, d=-2 022-1,则平面直角坐标系内的点A(a,b)与点A'(c,d)关于( )
A.y轴对称 B.x轴对称
C.原点对称 D.直线x=1对称
4.如图,四边形ABCD是中心对称图形,对称中心为点O,过点O的直线与AD、BC分别交于点E、F,则图中相等的线段有( )
A.3对 B.4对 C.5对 D.6对
5.如图,点O是 ABCD的对角线的交点,分别以AB,CD为斜边,向外作Rt△ABE和Rt△CDF,且Rt△ABE和Rt△CDF关于点O对称,连接EF.若AB=6,BC=8,则EF的最大值为( )
A.10 B.12 C.14 D.16
6.如图,若正方形EFGH是由正方形ABCD绕某点旋转得到的,则可以作为旋转中心的是( )
A.点M或点O或点N B.点E或点O或点C
C.点E或点O或点N D.点M或点O或点C
7.如图,在△OAB中,OA=OB,点A的坐标为(5,0),P是OA上一动点,将点P绕点C(0,1)逆时针旋转90°,当点P的对应点P'落在AB边上时,点P'的坐标为( )
A.(1,4) B.(4,1) C.(2,3) D.(3,2)
8.如图,在等边△ABC中,D是边AC上一动点,连接BD,将△BCD绕点B逆时针旋转60°得到△BAE,连接ED,若BC=10,则△AED的周长的最小值是( )
A.10 B.10
C.10+5 D.20
9.如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标分别为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交y轴于点P,若△ABC与△A'B'C'关于点P成中心对称,则点A'的坐标为( )
A.(-4,-5) B.(-5,-4)
C.(-3,-4) D.(-4,-3)
10.如图,矩形ABCD的顶点A、B分别在x轴、y轴上,OA=OB=2,AD=4,将矩形ABCD绕点O顺时针旋转,每次旋转90°,则第2 022次旋转结束时,点C的坐标为( )
A.(6,4) B.(-6,4)
C.(4,-6) D.(-4,6)
二、填空题(每小题4分,共24分)
11.在如图所示的方格纸(1格长为1个单位长度)中,△ABC的顶点都在格点上,将△ABC绕点O按顺时针方向旋转得到△A'B'C',若使△A'B'C'的顶点也在格点上,则其旋转角的度数至少为 .
12.已知点A(a,3)与点B(4,b)关于原点O对称,则a-b= .
13.如图所示的所有小正方形均全等,已有7个小正方形被涂黑,再涂黑一个小正方形,使涂黑部分是中心对称图形,则能被涂黑的小正方形是 .(填序号)
14.如图,在△ABC中,∠ACB=90°,将△ABC绕点A顺时针旋转90°,得到△ADE,连接BD,若AC=3,DE=1,则BD2= .
15.如图,△AOB中,AO=AB,点A的坐标为(3,4),点B在x轴上,将△AOB绕点B按顺时针方向旋转,得到△A'O'B,若点A'在线段OB的延长线上,则点O'的坐标为 .
16.如图,P是等边三角形ABC内的一点,且PA=3,PB=4,PC=5,以BC为边在△ABC外作△BQC≌△BPA,连接PQ,则以下结论中正确是 .(填序号)
①△BPQ是等边三角形,②△BQC可看作由△BPA绕点B顺时针旋转60°得到,③△PCQ是直角三角形,④∠APB=150° ,⑤∠APC=120°.
三、解答题(共46分)
17.(8分)如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(5,4),B(0,3),C(2,1).
(1)画出△ABC关于原点中心对称的△A1B1C1,并写出点C1的坐标;
(2)画出将△A1B1C1绕点C1按顺时针方向旋转90°所得的△A2B2C1.
18.(8分)如图,在4×4的方格纸中,△ABC的三个顶点都在格点上.
(1)在图①中,画出一个与△ABC成中心对称的格点三角形;
(2)在图②中,画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形;
(3)在图③中,画出△ABC绕着点C按顺时针方向旋转90°后的三角形.
19.(10分)如图,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,将△ADF绕点A顺时针旋转90°,得到△ABG.
(1)求证:△EAG≌△EAF;
(2)若正方形ABCD的边长为6,DF=3,求BE的长.
20.(10分)如图,菱形ABCD有一个内角等于60°,将∠MAN的顶点与该菱形的顶点A重合,以点A为旋转中心,按顺时针方向旋转∠MAN,使它的两边分别交CB、DC于点E、F,已知∠MAN=60°.
(1)如图①,当BE=DF时,AE与AF的数量关系是 ;
(2)旋转∠MAN,如图②,当BE≠DF时,(1)中的结论是否还成立 若成立,加以证明;若不成立,请说明理由.
21.(10分)如图,已知△AOB和△MON都是等腰直角三角形,∠AOB=∠MON=90°.
(1)如图a,连接AM,BN,求证:△AOM≌△BON;
(2)若将△MON绕点O顺时针旋转,
①如图b,当点N恰好在AB边上时,求证:BN2+AN2=2ON2;
②当点A、M、N在同一条直线上时,若OB=4,ON=3,请直接写出线段BN的长.
答案全解全析
1.A 观察图形可知,选项A中图形绕圆心旋转180°后能与自身重合,是中心对称图形,其他图形只是轴对称图形.
2.A ∵将△ABC绕点A顺时针旋转90°,得到△AB'C',∴AC=AC',∠CAC'=90°,∠BCA=∠AC'B',∴△ACC'是等腰直角三角形,∴∠AC'C=45°,∴∠AC'B'=∠AC'C-∠CC'B'=45°-32°=13°,∴∠ACB=∠AC'B'=13°.
3.C ∵a=-12 022=-1,b=2 022-1=,c=(-1)2 022=1, d=-2 022-1=-,∴A与A'关于原点对称.
4.C 如图,连接AC、BD,∵四边形ABCD是中心对称图形,对称中心为点O,∴AC、BD的交点为点O,OA=OC,OB=OD,∴四边形ABCD是平行四边形,∴AB=CD,BC=AD,易知OE=OF,AE=CF,BF=DE,∴题图中相等的线段共有5对.故选C.
5.C 如图,取AB的中点G,连接EG,OG,AC.∵点O是 ABCD的对角线的交点,∴点O是AC的中点,∴OG是△ABC的中位线.∵BC=8,∴OG=BC=4.∵点G是Rt△ABE斜边AB的中点,AB=6,∴EG=AB=3.∵OE≤EG+OG=3+4=7,∴当点E、G、O在一条直线上时,OE有最大值,为7.又∵Rt△ABE和Rt△CDF关于点O对称,∴OE=OF,∴EF的最大值为2×7=14.
6.A 若以点M为旋转中心,把正方形ABCD顺时针旋转90°,则A点的对应点为H,B点的对应点为E,C点的对应点为F,D点的对应点为G,则可得到正方形EFGH;若以点O为旋转中心,把正方形ABCD旋转180°,则A点的对应点为G,B点的对应点为H,C点的对应点为E,D点的对应点为F,则可得到正方形EFGH;若以点N为旋转中心,把正方形ABCD逆时针旋转90°,则A点的对应点为F,B点的对应点为G,C点的对应点为H,D点的对应点为E,则可得到正方形EFGH.故选A.
A 如图,作P'H⊥BC于点H,∵将点P绕点C(0,1)逆时针旋转90°得点P',
∴PC=P'C,∠PCP'=90°,∴∠PCO+∠P'CH=90°.
∵∠PCO+∠OPC=90°,∴∠OPC=∠HCP',又∵∠COP=∠CHP',PC=P'C,
∴△OPC≌△HCP'(AAS),∴P'H=OC=1.∵OA=OB,∠AOB=90°,∴∠OBA=45°,∵P'H⊥BC,∴∠HP'B=45°,∴∠OBA=∠HP'B,∴BH=HP'=1,∴OH=OB-BH=4,∴P'(1,4).
C 如图,作BF⊥AC于点F,∵△ABC是等边三角形,BC=10,∴AC=10,AF=FC=5.在Rt△BFC中,BF===5.∵将△BCD绕点B逆时针旋转60°得到△BAE,∴BD=BE,∠DBE=60°,CD=AE,∴△DBE是等边三角形,∴BD=DE,∴△AED的周长=AE+AD+DE=CD+AD+BD=AC+BD,∴当BD最小,即BD=BF=5时,△AED的周长最小,最小值=AC+BF=10+5.故选C.
A 如图,过点A作AD⊥x轴于点D,交BC于点E,则AE⊥BC.∵点B,C的坐标分别为(2,1),(6,1),∴BC=6-2=4,DE=1,∵AB=AC,AE⊥BC,∴BE=EC=BC=2,∴OD=6-2=4,
∵∠BAC=90°,∴AE=BC=2,∴AD=AE+DE=3,∴A(4,3).设直线AB的解析式为y=kx+b(k≠0),∵直线AB经过A(4,3),B(2,1)两点,∴解得∴直线AB的解析式为y=x-1,当x=0时,y=-1,∴P(0,-1),∵△ABC与△A'B'C'关于点P成中心对称,∴点P为AA'的中点,设A'(x,y),则0=,-1=,解得x=-4,y=-5,
∴A'(-4,-5).故选A.
C 如图,作CE⊥y轴于点E,连接OC.
∵OA=OB=2,∴∠ABO=∠BAO=45°.∵∠ABC=90°,∴∠CBE=45°.∵BC=AD=4,∴CE=BE=4,∴OE=OB+BE=6,∴C(-4,6).∵矩形ABCD绕点O顺时针旋转,每次旋转90°,则第1次旋转结束时,点C的坐标为(6,4);第2次旋转结束时,点C的坐标为(4,-6);第3次旋转结束时,点C的坐标为(-6,-4);第4次旋转结束时,点C的坐标为(-4,6);……,发现规律:每旋转4次为一个循环,∵2 022÷4=505……2,∴第2 022次旋转结束时,点C的坐标为(4,-6).
11.90°
解析 如图,连接OB、OB',∠BOB'=90°,∴旋转角的度数至少为90°.
12.-1
解析 ∵点A(a,3)与点B(4,b)关于原点O对称,∴a=-4,b=-3,则a-b=-4-(-3)=-1.
13.②
解析 观察图形可知,要使涂黑部分是中心对称图形,只能涂黑②号小正方形.
14.20
解析 由题可知:BC=DE=1,AB=AD,∠BAD=90°,∵在Rt△ABC中,AC=3,BC=1,∠ACB=90°,∴AD=AB===,
∵∠BAD=90°,∴BD2=AB2+AD2=10+10=20.
15.
解析 如图,作AC⊥OB于点C,O'D⊥A'B于点D,∵A(3,4),∴OC=3,AC=4,由勾股定理,得OA==5.
∵OA=AB,AC⊥OB,∴OB=2OC=2×3=6.由旋转可知,△A'O'B≌△AOB,∴O'B=BO=6,A'B=AB=5,S△AOB=S△A'O'B,即OB·AC=A'B·O'D,∴O'D=.由勾股定理,得BD=,
∴OD=OB+BD=6+=,∴点O'的坐标为.
16.①②③④
解析 ①∵△ABC是等边三角形,∴∠ABC=60°,∵△BQC≌△BPA,∴∠CBQ=∠ABP,QB=PB=4,QC=PA=3,∠BQC=∠BPA,∴∠PBQ=∠PBC+∠CBQ=∠PBC+∠ABP=∠ABC=60°,∴△BPQ是等边三角形,所以①正确;②由△BQC≌△BPA和∠ABC=∠PBQ=60°可知△BQC可看作由△BPA绕点B顺时针旋转60°得到,故②正确;③∵△BPQ是等边三角形,
∴PQ=PB=4,∵PQ2+QC2=42+32=25,PC2=52=25,∴PQ2+QC2=PC2,∴∠PQC=90°,∴△PCQ是直角三角形,所以③正确;④∵△BPQ是等边三角形,
∴∠PQB=60°,∴∠APB=∠BQC=∠BQP+∠PQC=60°+90°=150°,所以④正确;
⑤∠APC=360°-150°-60°-∠QPC=150°-∠QPC,
∵∠PQC=90°,PC≠2QC,∴∠QPC≠30°,∴∠APC≠120°,所以⑤错误.所以正确的是①②③④.
17.解析 (1)△A1B1C1如图所示,点C1的坐标为(-2,-1).
(2)△A2B2C1如图所示.
18.解析 (1)答案不唯一,如:
(2)答案不唯一,如:
(3)如图,△A'B'C即为所求.
19.解析 (1)证明:∵将△ADF绕点A顺时针旋转90°得到△ABG,
∴△ADF≌△ABG,
∴AF=AG,∠DAF=∠BAG.
∵∠DAB=90°,∠EAF=45°,
∴∠DAF+∠EAB=45°,
∴∠BAG+∠EAB=45°,∴∠EAG=45°,
∴∠EAF=∠EAG.
在△EAG和△EAF中,
∴△EAG≌△EAF(SAS).
(2)由(1)知,△ABG≌△ADF,△EAF≌△EAG,∴BG=DF=3,EF=EG,
设BE=x,则EF=GE=3+x,CE=6-x,
∵CD=6,DF=3,∴CF=CD-DF=3,
∵∠C=90°,∴(6-x)2+32=(3+x)2,
解得x=2,即BE=2.
20.解析 (1)AE=AF.
理由:∵四边形ABCD是菱形,∴AB=AD,∠B=∠D.
在△ABE和△ADF中,
∴△ABE≌△ADF(SAS),∴AE=AF.
(2)仍然成立.
理由如下:如图,连接AC,
∵四边形ABCD是菱形,
∴AB=BC=AD=CD,又由题意知∠B=∠D=60°,
∴△ABC是等边三角形,△ACD是等边三角形,
∴AB=AC,∠ACD=∠B=∠BAC=60°,
∵∠MAN=60°,∴∠MAN=∠BAC,∴∠BAE+∠EAC=∠CAF+∠EAC,∴∠BAE=∠CAF.
在△BAE和△CAF中,
∴△BAE≌△CAF(ASA),∴AE=AF.
21.解析 (1)证明:∵∠AOB=∠MON=90°,
∴∠AOM=∠BON,
在△AOM和△BON中,
∴△AOM≌△BON(SAS).
(2)①证明:如图1,连接AM.
图1
同(1)可证△AOM≌△BON,∴AM=BN,∠OAM=∠B=45°.∵∠OAB=∠B=45°,
∴∠MAN=∠OAM+∠OAB=90°,∴在Rt△AMN中,MN2=AN2+AM2.
∵△MON是等腰直角三角形,∴MN2=2ON2,∴BN2+AN2=2ON2.
②BN=.
详解:分两种情况:如图2,过点O作OH⊥MN于点H.
图2
∵△AOM≌△BON,∴AM=BN,
∵OM=ON=3,∠MON=90°,OH⊥MN,
∴MN=3,MH=HN=OH=,
∴AH===,
∴BN=AM=MH+AH=.
如图3,同法可证BN=AM=.
图3
同课章节目录
