沪科版九年级上册数学 21.6综合与实践 获得最大利润 教案
文档属性
| 名称 | 沪科版九年级上册数学 21.6综合与实践 获得最大利润 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 729.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-21 00:00:00 | ||
图片预览

文档简介
21.6 综合与实践 获取最大利润
教学目标
1.经历建立一次函数、二次函数模型的过程,逐步形成应用数学建模的方式 解决实际应用问题,增强数学的应用意识。
2.提高数学审题能力,理解实际应用问题中的数量关系及明确确自变量的取值范围.
3.提高综合应用函数知识和方法解决经济问题中最大利润问题。
教学重点:实际问题中数据转化成点的坐标并画图,建立一次、二次函数模型。
教学难点:选择合适的方法建立模型中二次函数的表达式。
教学设计
1)以题引入,温故知识。
问题1:若一种服装盈利y(万元)与销售数量(x万件)满足函数关系式y=-2x2+4x+5, 则盈利( )
A.最大值为5万元 B.最大值为7万元
C .最小值为5万元 D.最大值为6万元
设计目的:
1)有效帮助同学们理解二次函数基本知识如二次函数一般式,顶点式,二次函数顶点公式及函数增减性和最值。
2)帮助学生有意识注意到可以利用多种角度计算函数最值。
二)呈现实际问题,体验建立函数模型
阅读题意,思考问题
①在此问题中有哪些数量,它们之间什么关系?
②表格中呈现销量和销售单价之间有什么关系,你是怎么发现的,你有该怎么去说明你的判断?
设计目的:
1)有效问题可以提高同学们的阅读题目时的思考力。
2)数量关系是解决问题的重要因素,帮助同学们找到核心数量关系。
3)建立坐标系,画图像,直观说明两个量之间的关系类型。
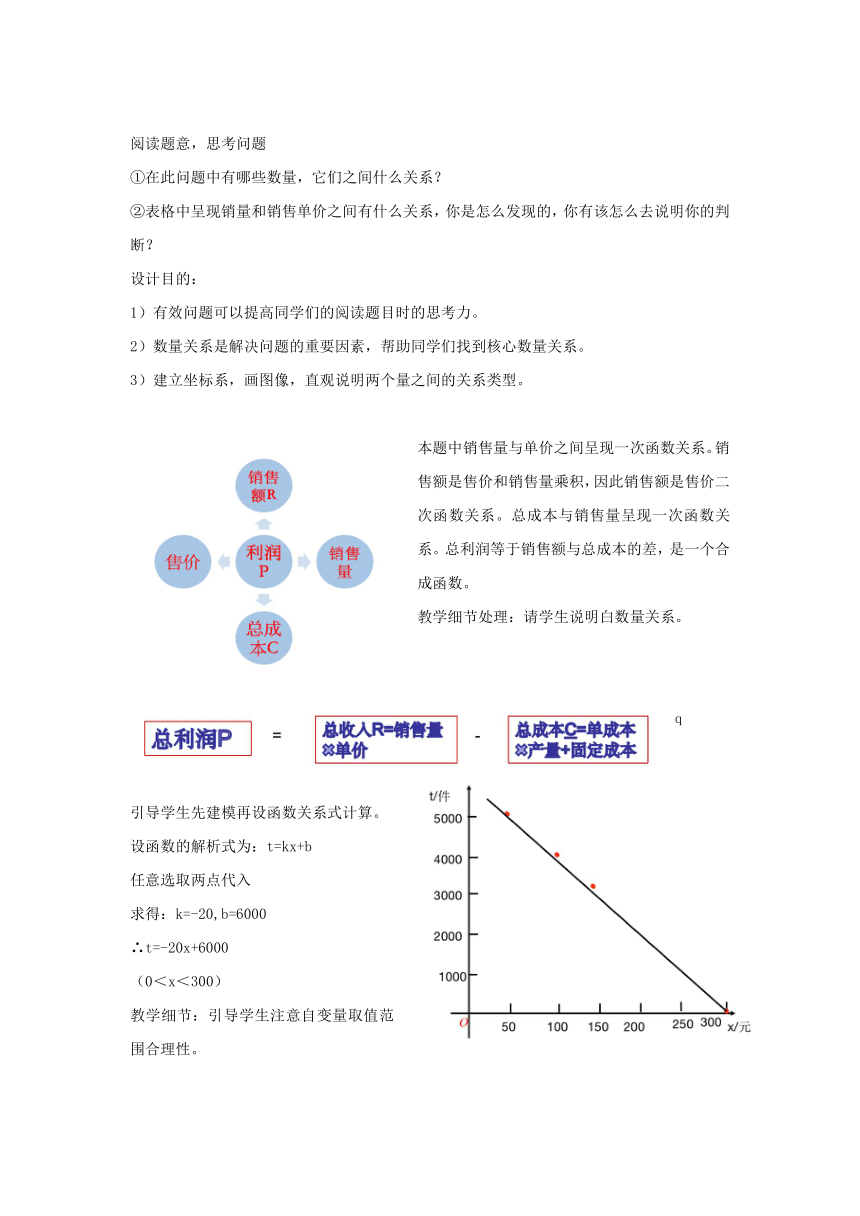
本题中销售量与单价之间呈现一次函数关系。销售额是售价和销售量乘积,因此销售额是售价二次函数关系。总成本与销售量呈现一次函数关系。总利润等于销售额与总成本的差,是一个合成函数。
教学细节处理:请学生说明白数量关系。
q
引导学生先建模再设函数关系式计算。
设函数的解析式为:t=kx+b
任意选取两点代入
求得:k=-20,b=6000
∴t=-20x+6000
(0<x<300)
教学细节:引导学生注意自变量取值范围合理性。
请同学们认真计算求最值。
教学细节处理:在计算过程中引导学生优化计算方法。在书写时明确最值确定需要二次项系数和自变量取值范围共同确定。
3)呈现问题2,学生自主合作解决
请你分析,当年销售量t和销售单价 x 分别是多少时,年利润 P 最大?并说说你有几种求解方法?与同学进行交流.
设计目的:问题2类似与问题1,但是有很大不同,表格中呈现数据大并且规律性呈现更隐蔽。其二不同在于数字庞大,更考验学生计算功底和耐心。
教学细节处理:给学生时间空间,给学生表达机会,给学生自我修正的机会。
4)教学总结:
通过今天学习,对比以往学习二次函数经历,你有什么感受?
老师在学生生成基础上强调几点
1)合理建立坐标系,通过图像呈现方式建模两个变量之间函数关系。
2)在实际应用中明确算理才能优化计算。
3)数学在实际应用广泛,比如计算机领域、医学领域、科技领域。
5)课后练习
1.某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元。经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) 50 60 70
销售量y(千克) 100 80 60
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式;
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
教学目标
1.经历建立一次函数、二次函数模型的过程,逐步形成应用数学建模的方式 解决实际应用问题,增强数学的应用意识。
2.提高数学审题能力,理解实际应用问题中的数量关系及明确确自变量的取值范围.
3.提高综合应用函数知识和方法解决经济问题中最大利润问题。
教学重点:实际问题中数据转化成点的坐标并画图,建立一次、二次函数模型。
教学难点:选择合适的方法建立模型中二次函数的表达式。
教学设计
1)以题引入,温故知识。
问题1:若一种服装盈利y(万元)与销售数量(x万件)满足函数关系式y=-2x2+4x+5, 则盈利( )
A.最大值为5万元 B.最大值为7万元
C .最小值为5万元 D.最大值为6万元
设计目的:
1)有效帮助同学们理解二次函数基本知识如二次函数一般式,顶点式,二次函数顶点公式及函数增减性和最值。
2)帮助学生有意识注意到可以利用多种角度计算函数最值。
二)呈现实际问题,体验建立函数模型
阅读题意,思考问题
①在此问题中有哪些数量,它们之间什么关系?
②表格中呈现销量和销售单价之间有什么关系,你是怎么发现的,你有该怎么去说明你的判断?
设计目的:
1)有效问题可以提高同学们的阅读题目时的思考力。
2)数量关系是解决问题的重要因素,帮助同学们找到核心数量关系。
3)建立坐标系,画图像,直观说明两个量之间的关系类型。
本题中销售量与单价之间呈现一次函数关系。销售额是售价和销售量乘积,因此销售额是售价二次函数关系。总成本与销售量呈现一次函数关系。总利润等于销售额与总成本的差,是一个合成函数。
教学细节处理:请学生说明白数量关系。
q
引导学生先建模再设函数关系式计算。
设函数的解析式为:t=kx+b
任意选取两点代入
求得:k=-20,b=6000
∴t=-20x+6000
(0<x<300)
教学细节:引导学生注意自变量取值范围合理性。
请同学们认真计算求最值。
教学细节处理:在计算过程中引导学生优化计算方法。在书写时明确最值确定需要二次项系数和自变量取值范围共同确定。
3)呈现问题2,学生自主合作解决
请你分析,当年销售量t和销售单价 x 分别是多少时,年利润 P 最大?并说说你有几种求解方法?与同学进行交流.
设计目的:问题2类似与问题1,但是有很大不同,表格中呈现数据大并且规律性呈现更隐蔽。其二不同在于数字庞大,更考验学生计算功底和耐心。
教学细节处理:给学生时间空间,给学生表达机会,给学生自我修正的机会。
4)教学总结:
通过今天学习,对比以往学习二次函数经历,你有什么感受?
老师在学生生成基础上强调几点
1)合理建立坐标系,通过图像呈现方式建模两个变量之间函数关系。
2)在实际应用中明确算理才能优化计算。
3)数学在实际应用广泛,比如计算机领域、医学领域、科技领域。
5)课后练习
1.某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元。经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) 50 60 70
销售量y(千克) 100 80 60
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式;
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
