Scratch趣味编程进阶课程-21-鸡兔同笼 课件
文档属性
| 名称 | Scratch趣味编程进阶课程-21-鸡兔同笼 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 信息科技(信息技术) | ||
| 更新时间 | 2022-12-26 14:58:11 | ||
图片预览






文档简介
(共27张PPT)
第21课
鸡兔同笼
学习目标
巩固与扩展
项目讨论
逻辑编程
1
2
3
4
1
今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?看一下“聪明猴”怎么通过编程的思维解决这道经典问题吧!
2
3
4
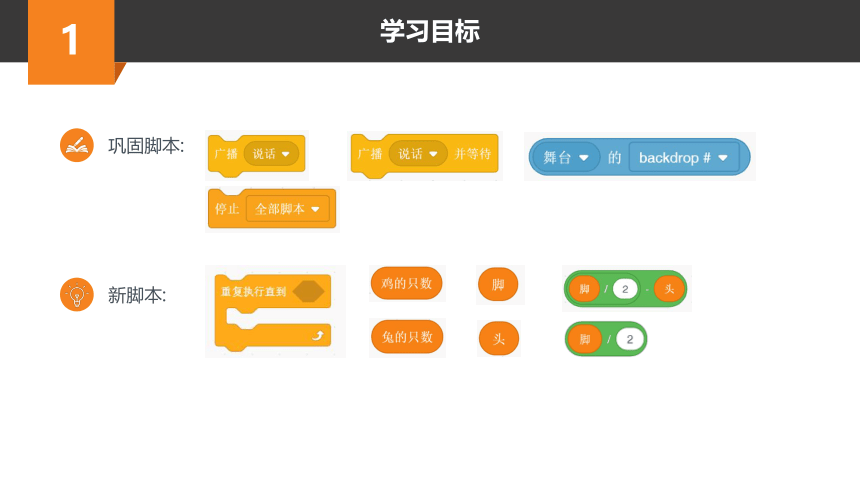
巩固“加减乘除”、“舞台背景编号” 、“广播” 、“变量”等脚本
学习灵活使用“询问回答”、“重复执行直到” 、“连接” 、“除法乘法” 、等脚本
综合应用所学脚本完成编程项目并扩展
新脚本:
巩固脚本:
1.本节课用到的角色
2.本节课用到的背景
Monkey2
窗户旁
《鸡兔同笼》
笼子
Rare
Rooster
1.头有35个头,脚有94只,各有多少鸡和兔?
2.假如变化一下头和脚的数量,你还能计算出来有多少鸡和脚么?
3.一共设置了几个变量?
4.咦,小猴子为什么这么聪明呢?
这就是典型的鸡兔同笼问题了,一会儿老师会详细讲解
当然啦,用咱们的程序直接就可以得出结果
4个,分别是:兔的只数、鸡的只数、头、脚
因为它学过鸡兔同笼这个题目了,并且他也会编程
《鸡兔同笼》
1.鸡兔同笼讲解
1.鸡兔同笼问题
一只鸡有:1头、2脚
大家能算出来有多几只鸡和兔么?
翻译:有若干只鸡和兔在同个笼子里,从上面数,有35个头;从下面数,有94只脚。求笼中各有几只鸡和兔?
“鸡兔同笼问题”是我国古算书《孙子算经》中著名的数学问题,其内容是:今有雉(鸡)兔同笼,上有三十五头,下有九十四足。问雉兔各几何
一只兔有:1头、4脚
1.鸡兔同笼讲解
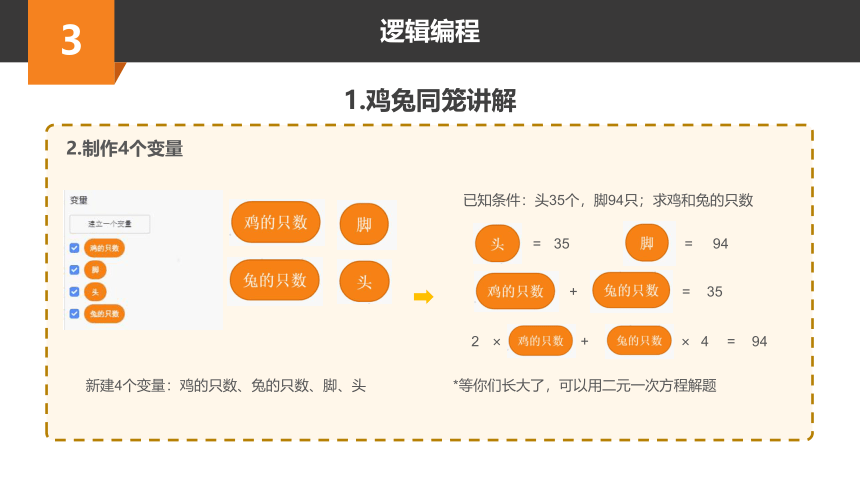
2.制作4个变量
新建4个变量:鸡的只数、兔的只数、脚、头
已知条件:头35个,脚94只;求鸡和兔的只数
+
=
35
=
35
94
=
2
×
+
×
4
94
=
*等你们长大了,可以用二元一次方程解题
1.鸡兔同笼讲解
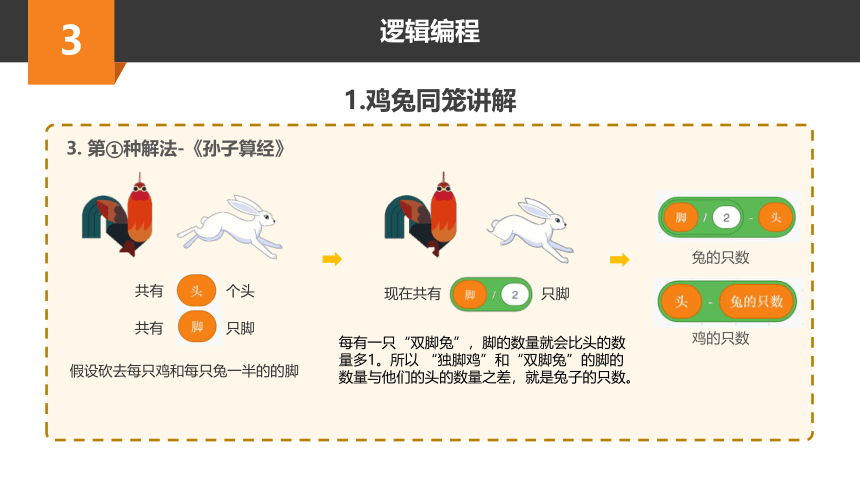
3. 第①种解法-《孙子算经》
兔的只数
假设砍去每只鸡和每只兔一半的的脚
每有一只“双脚兔”,脚的数量就会比头的数量多1。所以 “独脚鸡”和“双脚兔”的脚的数量与他们的头的数量之差,就是兔子的只数。
鸡的只数
共有
个头
共有
只脚
现在共有
只脚
1.鸡兔同笼讲解
3. 第①种解法-《孙子算经》
最终的程序
1.鸡兔同笼讲解
4. 第②种解法-抬脚法
假设鸡和兔都抬起2只脚,
共有
那总共抬起来了
只脚
还剩下
只脚
只脚
鸡的只数
剩下的都是兔子的脚,每个兔子有2只脚
所以兔子共有
只
鸡和兔的数量总共有
只
1.鸡兔同笼讲解
4. 第②种解法-抬脚法
鸡的只数
最终的程序
2.猴子出题的程序
1.设定鸡和兔的头数和脚数
使用询问脚本,将输入的数字设定为:头的数量和鸡的数量
假如有35个头,这一句的问句变成:鸡兔同笼。有35个头,你要设定几个脚?
3.猴子的其他程序
1.猴子说话的程序
切换造型的程序
最终会定型在:monkey2-c
如果用下一个造型这个脚本,最后定在哪一个造型不一定,需要咱们自己查看角色造型的数量,才能知道最后会变成哪个造型
3.猴子的其他程序
2.猴子的总程序
等待8秒是为了让其它角色执行完程序
后再问下一个问题
让鸡和兔说出正确答案
4.笼子的程序
1.笼子的程序
小绿旗被点击之后显示
并且要盖住兔子和公鸡
5.鸡的程序
1.鸡接收到广播说出答案
处于笼子前面
这一段程序是让鸡切换造型,切换持续的时间是2秒钟
切换造型
大小变化一下
又恢复原状
5.鸡的程序
2.鸡说出答案
说出正确答案
等待1秒是因为前面切换造型的时候花了一秒钟时间
6.兔的程序
1.兔的程序
其它程序和鸡的程序类似,这里等待3秒是为了让鸡先说完话,然后兔子再说话
因为兔子很懂礼貌哦
6.兔的程序
2.兔的接收到广播的程序
这里的等待3秒也是为了让鸡先说完话,然后兔子再说话
Q1:明明给小猴子编程,编写了这样的程序,会发生什么现象呢?
A1:将头增加回答,这个脚本错误,而是应该将头设定为回答。发生什么现象咱们自己测试一下吧。
Q&A
Q2:明明发现有时候输入头和腿的数量以后,程序自动计算的鸡和兔的数量会出现负数是为什么呢?
A2:因为不能出现符合条件的组合,这个数字是咱们自己构造的,得根据实际情况来哦。
比如头5个,腿1个,这样的组合根本不可能存在。
Q&A
(1)
(2)
加减乘除的混合使用,巩固学习拼接复杂编程积木块儿,巩固学习相应的数学原理
用计时器来控制某一段脚本的执行时间,结合重复执行直到,实现这个功能
知识点巩固
(1)
知识点巩固
数学:假设法的应用
今天鸡兔同笼的编程课,讲了两种方法,都是假设法
①假设都去掉一半的脚
②假设鸡和兔都去掉2个脚
算法不同,方法相同,孩子们要灵活应用,碰到类似的问题,可以用同样的方法来制作解答
明明给猴子的程序进行了这样的编程,那到底是正确还是错误呢?( )
A
B
源码测试
正确
错误
答案:
解析:
在前面的程序一样的情况下,这两个脚本的含义是一样的,咱们可以赋值给脚和头,测试一下吧
A
源码测试
第21课
鸡兔同笼
学习目标
巩固与扩展
项目讨论
逻辑编程
1
2
3
4
1
今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?看一下“聪明猴”怎么通过编程的思维解决这道经典问题吧!
2
3
4
巩固“加减乘除”、“舞台背景编号” 、“广播” 、“变量”等脚本
学习灵活使用“询问回答”、“重复执行直到” 、“连接” 、“除法乘法” 、等脚本
综合应用所学脚本完成编程项目并扩展
新脚本:
巩固脚本:
1.本节课用到的角色
2.本节课用到的背景
Monkey2
窗户旁
《鸡兔同笼》
笼子
Rare
Rooster
1.头有35个头,脚有94只,各有多少鸡和兔?
2.假如变化一下头和脚的数量,你还能计算出来有多少鸡和脚么?
3.一共设置了几个变量?
4.咦,小猴子为什么这么聪明呢?
这就是典型的鸡兔同笼问题了,一会儿老师会详细讲解
当然啦,用咱们的程序直接就可以得出结果
4个,分别是:兔的只数、鸡的只数、头、脚
因为它学过鸡兔同笼这个题目了,并且他也会编程
《鸡兔同笼》
1.鸡兔同笼讲解
1.鸡兔同笼问题
一只鸡有:1头、2脚
大家能算出来有多几只鸡和兔么?
翻译:有若干只鸡和兔在同个笼子里,从上面数,有35个头;从下面数,有94只脚。求笼中各有几只鸡和兔?
“鸡兔同笼问题”是我国古算书《孙子算经》中著名的数学问题,其内容是:今有雉(鸡)兔同笼,上有三十五头,下有九十四足。问雉兔各几何
一只兔有:1头、4脚
1.鸡兔同笼讲解
2.制作4个变量
新建4个变量:鸡的只数、兔的只数、脚、头
已知条件:头35个,脚94只;求鸡和兔的只数
+
=
35
=
35
94
=
2
×
+
×
4
94
=
*等你们长大了,可以用二元一次方程解题
1.鸡兔同笼讲解
3. 第①种解法-《孙子算经》
兔的只数
假设砍去每只鸡和每只兔一半的的脚
每有一只“双脚兔”,脚的数量就会比头的数量多1。所以 “独脚鸡”和“双脚兔”的脚的数量与他们的头的数量之差,就是兔子的只数。
鸡的只数
共有
个头
共有
只脚
现在共有
只脚
1.鸡兔同笼讲解
3. 第①种解法-《孙子算经》
最终的程序
1.鸡兔同笼讲解
4. 第②种解法-抬脚法
假设鸡和兔都抬起2只脚,
共有
那总共抬起来了
只脚
还剩下
只脚
只脚
鸡的只数
剩下的都是兔子的脚,每个兔子有2只脚
所以兔子共有
只
鸡和兔的数量总共有
只
1.鸡兔同笼讲解
4. 第②种解法-抬脚法
鸡的只数
最终的程序
2.猴子出题的程序
1.设定鸡和兔的头数和脚数
使用询问脚本,将输入的数字设定为:头的数量和鸡的数量
假如有35个头,这一句的问句变成:鸡兔同笼。有35个头,你要设定几个脚?
3.猴子的其他程序
1.猴子说话的程序
切换造型的程序
最终会定型在:monkey2-c
如果用下一个造型这个脚本,最后定在哪一个造型不一定,需要咱们自己查看角色造型的数量,才能知道最后会变成哪个造型
3.猴子的其他程序
2.猴子的总程序
等待8秒是为了让其它角色执行完程序
后再问下一个问题
让鸡和兔说出正确答案
4.笼子的程序
1.笼子的程序
小绿旗被点击之后显示
并且要盖住兔子和公鸡
5.鸡的程序
1.鸡接收到广播说出答案
处于笼子前面
这一段程序是让鸡切换造型,切换持续的时间是2秒钟
切换造型
大小变化一下
又恢复原状
5.鸡的程序
2.鸡说出答案
说出正确答案
等待1秒是因为前面切换造型的时候花了一秒钟时间
6.兔的程序
1.兔的程序
其它程序和鸡的程序类似,这里等待3秒是为了让鸡先说完话,然后兔子再说话
因为兔子很懂礼貌哦
6.兔的程序
2.兔的接收到广播的程序
这里的等待3秒也是为了让鸡先说完话,然后兔子再说话
Q1:明明给小猴子编程,编写了这样的程序,会发生什么现象呢?
A1:将头增加回答,这个脚本错误,而是应该将头设定为回答。发生什么现象咱们自己测试一下吧。
Q&A
Q2:明明发现有时候输入头和腿的数量以后,程序自动计算的鸡和兔的数量会出现负数是为什么呢?
A2:因为不能出现符合条件的组合,这个数字是咱们自己构造的,得根据实际情况来哦。
比如头5个,腿1个,这样的组合根本不可能存在。
Q&A
(1)
(2)
加减乘除的混合使用,巩固学习拼接复杂编程积木块儿,巩固学习相应的数学原理
用计时器来控制某一段脚本的执行时间,结合重复执行直到,实现这个功能
知识点巩固
(1)
知识点巩固
数学:假设法的应用
今天鸡兔同笼的编程课,讲了两种方法,都是假设法
①假设都去掉一半的脚
②假设鸡和兔都去掉2个脚
算法不同,方法相同,孩子们要灵活应用,碰到类似的问题,可以用同样的方法来制作解答
明明给猴子的程序进行了这样的编程,那到底是正确还是错误呢?( )
A
B
源码测试
正确
错误
答案:
解析:
在前面的程序一样的情况下,这两个脚本的含义是一样的,咱们可以赋值给脚和头,测试一下吧
A
源码测试
同课章节目录
