Scratch趣味编程进阶课程-29-分配任务、最大公约数 课件
文档属性
| 名称 | Scratch趣味编程进阶课程-29-分配任务、最大公约数 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2022-12-26 15:00:05 | ||
图片预览




文档简介
(共19张PPT)
第29课
分配任务与最大公约数
学习目标
巩固与扩展
项目讨论
逻辑编程
1
2
3
4
1
Ai时代,人工智能担任起了任务调度、提高社会效率的重任,比如共享单车。人工智能的背后均是有各种算法与机制组成。这节课我们通过一个简单的任务分配问题来了解,人工智能是怎样做社会调度的指挥官的!
2
3
4
巩固“变量”、“数学运算”等脚本
学习“询问并等待”、“回答” 、“列表” 、“如果、否则” 、“重复执行10次” 等新脚本
综合应用所学脚本完成编程项目并扩展
新脚本:
巩固脚本:
1.本节课用到的角色
2.本节课用到的背景
Cat
初始白色背景
《分配任务》
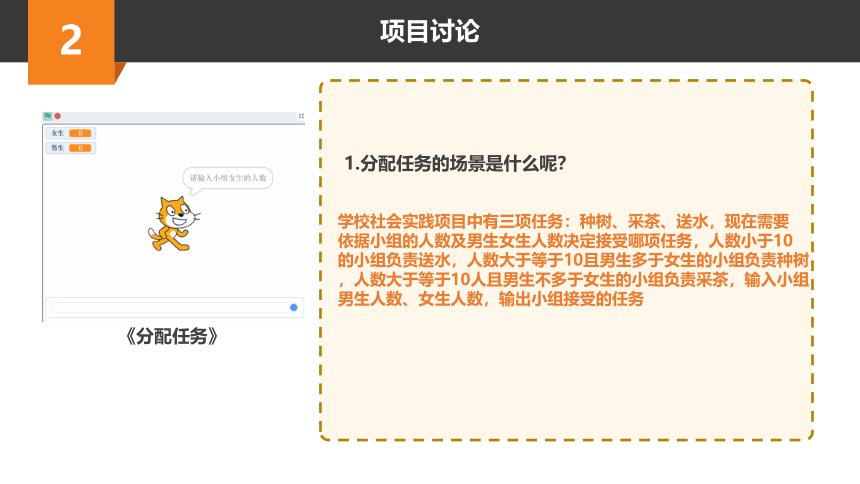
1.分配任务的场景是什么呢?
《分配任务》
学校社会实践项目中有三项任务:种树、采茶、送水,现在需要
依据小组的人数及男生女生人数决定接受哪项任务,人数小于10
的小组负责送水,人数大于等于10且男生多于女生的小组负责种树
,人数大于等于10人且男生不多于女生的小组负责采茶,输入小组
男生人数、女生人数,输出小组接受的任务
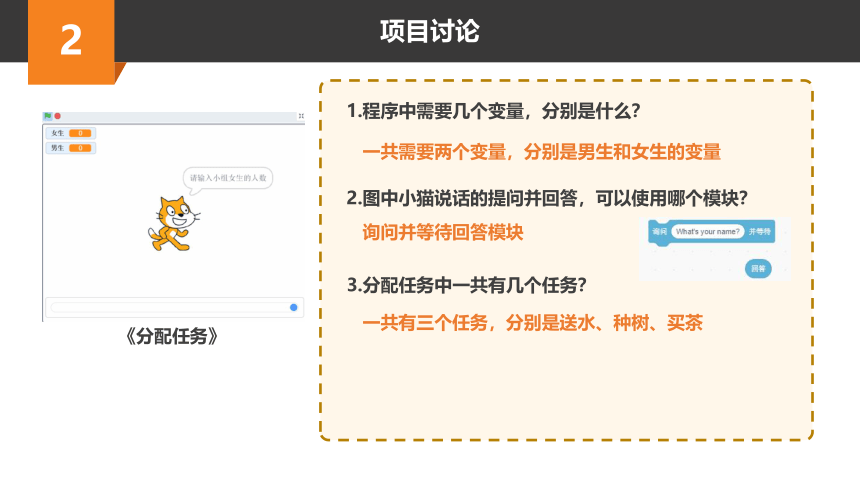
1.程序中需要几个变量,分别是什么?
2.图中小猫说话的提问并回答,可以使用哪个模块?
3.分配任务中一共有几个任务?
一共需要两个变量,分别是男生和女生的变量
询问并等待回答模块
一共有三个任务,分别是送水、种树、买茶
《分配任务》
1.解题分析
1.任务解读
开始
输入男女生人数
总人数小于10
是
送水
男生大于女生
否
是
否
种树
买茶
2.分配任务程序
1.建立变量,变量归0
变量有两个分别是男生与女生
询问并等待模块运用,需要注意将对应设定为回答
2.输入男生与女生人数
3.条件判断输出任务
如果...那么...否则...运用
1最大公约数的应用场景是什么样子的呢?
一张长105cm、宽75cm的长方形铁皮,要分成若干张大小完全相同的正方形铁皮且无剩余,这张长方形铁皮最少可以分成多少张正方形铁皮?
问题分析:要使长方形铁皮分成的正方形铁皮的张数最少,即要使正方形的铁皮边长最大。同时要使长方形铁皮分成大小相同的正方形铁皮且无剩余,即正方形的边长是长方形的长和宽的最大公因数。最少可以分得的正方形铁皮张数:长方形的面积/边长最大的正方形面积
《最大公因数》
1.程序中需要几个变量,分别是什么?
2.假设正方形面积固定,如何才能知道有多少个?
3.怎样才能保证剪掉后的正方形没有剩余的铁皮呢?
一共需要三个变量,分别是长、宽、公因数i
使用运算模块乘法求出长方形面积,再用长方形面积除以正方形面积。
先计算出长与宽的最大公因数
《最大公因数》
1.解题分析
1.求取长与宽的最大公因数
最大公因数,也称最大公约数、最大公因子,指两个或多个整数共有约数中最大的一个。
由此可知,正方形的面积为15X15=225
长方形的长为105可以分解为3X5X7
长方形的宽为75可以分解为3X5X5
我们可以发现长与宽的公因子是3和5,故最大公因数为15.
正方形的个数=(105X75)/225.
故结果为35个。
2.程序编写
1.建立列表
2.设定初始变量值
3.求取公因数
重复执行的次数为宽的大小
5.输出结果
2.长方形面积除以正方形面积得出结果,并输出。
Q1:明明编写的求取公因数的程序,编写了这样的程序,会发生什么现象呢?
A1:公因数i增加模块放错了位置,公因数只显示1,就不在进行下去了哦。
Q&A
(1)
(2)
上面的是长方形面积公式,下面的是正方形的面积公式
公因数,长与宽必须同时满足。
知识点巩固
如果给出长方形的长为92,宽为37.那么可以剪出多少个正方形,不剩余铁皮呢?
源码测试
答案:
解析:
因为92与37的最大公约是1,
所以正方形的边长就是1,面积为1.长方形的面积为92X37=3404
3404/1=3404
3404
源码测试
第29课
分配任务与最大公约数
学习目标
巩固与扩展
项目讨论
逻辑编程
1
2
3
4
1
Ai时代,人工智能担任起了任务调度、提高社会效率的重任,比如共享单车。人工智能的背后均是有各种算法与机制组成。这节课我们通过一个简单的任务分配问题来了解,人工智能是怎样做社会调度的指挥官的!
2
3
4
巩固“变量”、“数学运算”等脚本
学习“询问并等待”、“回答” 、“列表” 、“如果、否则” 、“重复执行10次” 等新脚本
综合应用所学脚本完成编程项目并扩展
新脚本:
巩固脚本:
1.本节课用到的角色
2.本节课用到的背景
Cat
初始白色背景
《分配任务》
1.分配任务的场景是什么呢?
《分配任务》
学校社会实践项目中有三项任务:种树、采茶、送水,现在需要
依据小组的人数及男生女生人数决定接受哪项任务,人数小于10
的小组负责送水,人数大于等于10且男生多于女生的小组负责种树
,人数大于等于10人且男生不多于女生的小组负责采茶,输入小组
男生人数、女生人数,输出小组接受的任务
1.程序中需要几个变量,分别是什么?
2.图中小猫说话的提问并回答,可以使用哪个模块?
3.分配任务中一共有几个任务?
一共需要两个变量,分别是男生和女生的变量
询问并等待回答模块
一共有三个任务,分别是送水、种树、买茶
《分配任务》
1.解题分析
1.任务解读
开始
输入男女生人数
总人数小于10
是
送水
男生大于女生
否
是
否
种树
买茶
2.分配任务程序
1.建立变量,变量归0
变量有两个分别是男生与女生
询问并等待模块运用,需要注意将对应设定为回答
2.输入男生与女生人数
3.条件判断输出任务
如果...那么...否则...运用
1最大公约数的应用场景是什么样子的呢?
一张长105cm、宽75cm的长方形铁皮,要分成若干张大小完全相同的正方形铁皮且无剩余,这张长方形铁皮最少可以分成多少张正方形铁皮?
问题分析:要使长方形铁皮分成的正方形铁皮的张数最少,即要使正方形的铁皮边长最大。同时要使长方形铁皮分成大小相同的正方形铁皮且无剩余,即正方形的边长是长方形的长和宽的最大公因数。最少可以分得的正方形铁皮张数:长方形的面积/边长最大的正方形面积
《最大公因数》
1.程序中需要几个变量,分别是什么?
2.假设正方形面积固定,如何才能知道有多少个?
3.怎样才能保证剪掉后的正方形没有剩余的铁皮呢?
一共需要三个变量,分别是长、宽、公因数i
使用运算模块乘法求出长方形面积,再用长方形面积除以正方形面积。
先计算出长与宽的最大公因数
《最大公因数》
1.解题分析
1.求取长与宽的最大公因数
最大公因数,也称最大公约数、最大公因子,指两个或多个整数共有约数中最大的一个。
由此可知,正方形的面积为15X15=225
长方形的长为105可以分解为3X5X7
长方形的宽为75可以分解为3X5X5
我们可以发现长与宽的公因子是3和5,故最大公因数为15.
正方形的个数=(105X75)/225.
故结果为35个。
2.程序编写
1.建立列表
2.设定初始变量值
3.求取公因数
重复执行的次数为宽的大小
5.输出结果
2.长方形面积除以正方形面积得出结果,并输出。
Q1:明明编写的求取公因数的程序,编写了这样的程序,会发生什么现象呢?
A1:公因数i增加模块放错了位置,公因数只显示1,就不在进行下去了哦。
Q&A
(1)
(2)
上面的是长方形面积公式,下面的是正方形的面积公式
公因数,长与宽必须同时满足。
知识点巩固
如果给出长方形的长为92,宽为37.那么可以剪出多少个正方形,不剩余铁皮呢?
源码测试
答案:
解析:
因为92与37的最大公约是1,
所以正方形的边长就是1,面积为1.长方形的面积为92X37=3404
3404/1=3404
3404
源码测试
同课章节目录
