苏教版(2019)高中数学必修第一册《7.4三角函数应用》精品课件(共19张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学必修第一册《7.4三角函数应用》精品课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-22 22:27:15 | ||
图片预览






文档简介
(共19张PPT)
苏教版同步教材精品课件
7.4 三角函数应用
情境引入
既然大到宇宙天体的运动,小到质点的运动以及现实世界中具有周期性变化的现象无处不在,那么究竟怎样用三角函数解决这些具有周期性变化的问题?它到底能发挥哪些作用呢?
学生畅所欲言,将生活中、物理中的周而复始现象与三角函数建立关系.
设计意图:体会三角函数是解决周而复始现象的重要数学模型,体会三角函数在生活中的重要应用,学会利用数学的语言表达世界,培养学生的直观想象能力.
探究新知
问题1:(1)回忆从前所学,指数函数、对数函数以及幂函数的模型都是常用来描述现实世界中的哪些规律的?(2)数学模型是什么?建立数学模型的方法是什么?
(3)解决问题的一般步骤是什么?
(4)怎样处理收集到的数据?
师生互动,唤起回忆,充分复习前面学习过的建立数学模型的方法与过程对课前已经做好复习的学生给予表扬,并鼓励他们类比以前所学知识方法,继续探究新的数学模型.对还没有进入状态的学生,教师要帮助他们回忆并快速激起相应的知识方法:收集数据→画散点图→选择函数模型→求解函数模型→检验→用函数模型解释实际问题.
讨论结果:
(1)描述现实世界中不同增长规律的函数模型.
(2)简单地说,数学模型就是把实际问题用数学语言抽象概括,再从数学角度来反映或近似地反映实际问题时,所得出的关于实际问题的数学描述建立数学模型的方法就是把实际问题加以抽象概括,建立相应的数学模型,利用这些模型来研究实际问题的一般数学方法.
探究新知
(3)解决问题的一般步骤是:
①审题:逐字逐句阅读题意,审清楚题目条件、要求、理解数学关系;
②建模:分析题目变化趋势,选择适当的函数模型;
③求解:对所建立的数学模型进行分析研究得到数学结论;
④还原:把数学结论还原为实际问题的答案.
(4)画出散点图,分析它的变化趋势,确定合适的函数模型.
设计意图:引导学生回顾指数函数、对数函数以及幂函数模型的建立方法,为本节课的学习做好铺垫,让学生体会由实际问题建立三角函数模型的过程,培养和发展数学建模、数学抽象、直观想象等核心素养.
探究新知
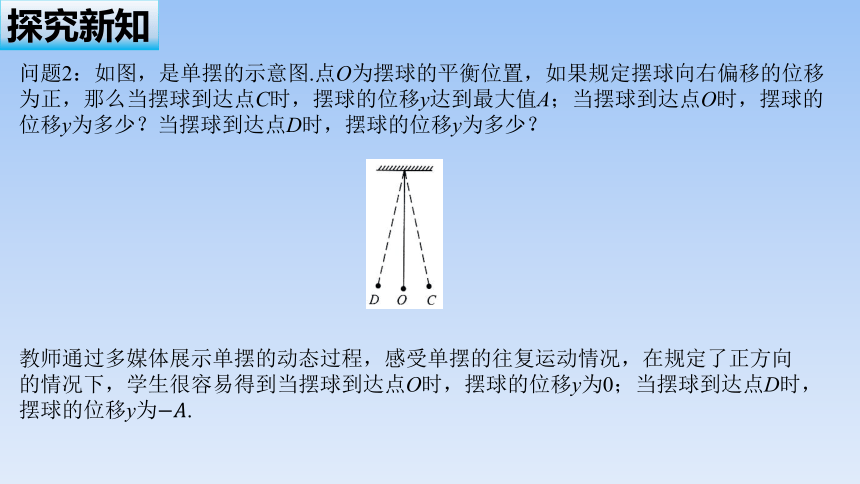
问题2:如图,是单摆的示意图.点O为摆球的平衡位置,如果规定摆球向右偏移的位移为正,那么当摆球到达点C时,摆球的位移y达到最大值A;当摆球到达点O时,摆球的位移y为多少?当摆球到达点D时,摆球的位移y为多少?
教师通过多媒体展示单摆的动态过程,感受单摆的往复运动情况,在规定了正方向的情况下,学生很容易得到当摆球到达点O时,摆球的位移y为0;当摆球到达点D时,摆球的位移y为.
探究新知
教师再利用多媒体展示单摆随时间的位移变化图象的形成过程,让学生感受单摆的运动位移与时间的关系,理解单摆的位移与时间关系是模型.从而自然理解三角函数表达式中每一个量的物理意义:
x表示时间,y表示相对于平衡位置的偏离;
A表示物体运动时离开平衡位置的最大距离,称为振幅;
往复运动一次所需的时间称为这个运动的周期;
单位时间内往复运动的次数为运动的频率;
称为相位,时的相位称为初相位.
设计意图:感受三角函数在物理中的应用,理解简谐振动的图象是三角函数模型,掌握中每一个量的物理意义,同时培养学生的数学应用意识,感受数学与物理的密切联系,通过视频展示,培养学生的直观想象能力和逻辑推理能力,为下面的应用做好准备.
典例剖析
例1、在下图中,点O为做简谐运动的物体的平衡位置,取向右的方向为物体位移的正方向已知振幅为3cm周期为3s,且物体向右运动到距平衡位置最远处时开始计时求:
(1)设x和t之间的函数关系为.
则由,可得.
当时,有,即.
又,可得.
因此所求函数关系为,
即.
解析
(1)物体对平衡位置的位移x(单位:cm)和时间t(单位:s)之间的函数关系;
(2)该物体在s时的位置.
典例剖析
例1、在下图中,点O为做简谐运动的物体的平衡位置,取向右的方向为物体位移的正方向已知振幅为3cm周期为3s,且物体向右运动到距平衡位置最远处时开始计时求:
(2)令,得,故该物体在s时的位置是在O点的左侧且距O点1.5cm处.
解析
(1)物体对平衡位置的位移x(单位:cm)和时间t(单位:s)之间的函数关系;
(2)该物体在s时的位置.
设计意图:利用弹簧振子的振动,引入三角函数模型的建立过程,感受三角函数在物理中的广泛应用.
典例剖析
变式训练:一根长lcm的线,一端固定,另一端悬挂一个小球,小球摆动时离开平衡位置的位移s(cm)与时间t(s)的函数关系式是,其中g是重力加速度,当小球摆动的周期是1s时,线长 ( )
A. B. C. D.
单摆与弹簧振动一样,是简谐振动,其振动曲线是三角函数模型.因为周期,所以,则.
解析
D
典例剖析
例2、一半径为3m的水轮如图所示,水轮圆心O距离水面2m,已知水轮每分钟逆时针转动4圈,且当水轮上点P从水中浮现时(图中点)开始计算时间.
(1)如上图,建立平面直角坐标系.
设角是以为始边,为终边的角.
当OP在ts内所转过的角为,可知以为始边,OP为终边的角为,故P点纵坐标为,则.
当时,,可得,
因为,所以,故所求函数关系式为.
解析
(1)将点P到水面的距离z(单位:m在水面下,则z为负数)表示为时间t(单位:s)的函数;
(2)点P第一次到达最高点大约要多长时间?
典例剖析
例2、一半径为3m的水轮如图所示,水轮圆心O距离水面2m,已知水轮每分钟逆时针转动4圈,且当水轮上点P从水中浮现时(图中点)开始计算时间.
(2)令,得.
取,解得.
故点P第一次到达最高点大约需要5.5s.
解析
(1)将点P到水面的距离z(单位:m在水面下,则z为负数)表示为时间t(单位:s)的函数;
(2)点P第一次到达最高点大约要多长时间?
典例剖析
变式训练:某地一天的温度(单位:℃)随时间(单位:小时的变化近似满足函数关系:,且早上8时的温度为24℃.
(1)求函数的解析式,并判断这一天的最高温度是多少.出现在何时?
(2)当地有一通宵营业的超市,为了节省开支,规定在环境温度超过28℃时,开启中央空调降温,否则关闭中央空调,问中央空调应在何时开启?何时关闭?
(1)根据题意求出的值,确定函数的解析式利用正弦函数的图象与性质求得出现最高温时t的值;
(2)令,求出t的值即可得出结论.
分析
解析
(1),且早上8时的温度为24℃,即,
,解得.又时,.
.
又时,取得最大值,且,
令,解得,即这一天在14时(也是下午2时)出现最高温度,最高温度是32℃.
典例剖析
变式训练:某地一天的温度(单位:℃)随时间(单位:小时的变化近似满足函数关系:,且早上8时的温度为24℃.
(1)求函数的解析式,并判断这一天的最高温度是多少.出现在何时?
(2)当地有一通宵营业的超市,为了节省开支,规定在环境温度超过28℃时,开启中央空调降温,否则关闭中央空调,问中央空调应在何时开启?何时关闭?
(1)根据题意求出的值,确定函数的解析式利用正弦函数的图象与性质求得出现最高温时t的值;
(2)令,求出t的值即可得出结论.
分析
解析
(2)依题意知,令,可得.
,
或,解得或,即中央空调应在上午10时开启,下午18时(即下午6时)关闭.
设计意图:体会三角函数模型在生活中应用,巩固实际问题的解决方法和步骤.
典例剖析
例3、如图是某个弹簧振子(简称振子),它在完成一次全振动的过程中,时间t(单位:s)与位移y(单位:mm)之间的对应数据如下表所示.试根据这些数据确定这个振子的位移关于时间的函数解析式.
请你查阅资料,了解振子的运动原理解.
振子的振动具有循环往复的特点,由振子振动的物理学原理可知,其位移随时间的变化规律可以用函数来刻画.根据已知数据作出散点图,如图所示.
典例剖析
由数据表和散点图可知,振子振动时位移的最大值为20mm,因此;振子振动的周期为0.6s,即解得;再由初始状态()振子的位移为mm,可得,因此.所以这个振子的位移关于时间的函数解析式为.
典例剖析
归纳总结:现实生活中存在大量类似弹簧振子的运动,如钟摆的摆动,水中浮标的上下浮动,琴弦的振动,等等这些都是物体在某一中心位置附近循环往复的运动.在物理学中,把物体受到的力(总是指向平衡位置)正比于它离开平衡位置的距离的运动称为“简谐运动”.可以证明,在适当的直角坐标系下,简谐运动可以用函数表示,其中.描述简谐运动的物理量,如振幅、周期和频率等都与这个解析式中的常数有关:A就是这个简谐运动的振幅,它是做简谐运动的物体离开平衡位置的最大距离;这个简谐运动的周期是,它是做简谐运动的物体往复运动一次所需要的时间;这个简谐运动的频率由公式给出,它是做简谐运动的物体在单位时间内往复运动的次数;称为相位;时的相位称为初相位.
设计意图:通过对典型问题的分析解决,发展学生的数学建模、逻辑推理、直观想象、数学抽象、数学运算等核心素养.
典例剖析
变式训练:如图(1)所示的是某次实验测得的交变电流I(单位:A)随时间t(单位:s)变化的图象(频率为50Hz).将测得的图象放大,得到图(2).
(1)求电流I随时间t变化的函数解析式;
(2)当时,求电流I.
请你查阅资料,了解交变电流的产生原理.
解析
由交变电流的产生原理可知,电流I随时间t的变化规律可用来刻画,其中表示频率,A表示振幅,表示初相.
由图(2)可知,电流最大值为5A,因此;电流变化的周期为s,频率为50Hz,即,解得;再由初始状态()的电流约为4.33A,可得,因此约为.
所以电流Ⅰ随时间t变化的函数解析式是.
当时,;当时,;
当时,;当时,.
设计意图:感受三角函数模型在物理交流电中的应用,培养学生的数据分析能力和数学应用意识.
课堂小结
教师引导学生总结这节课学习的数学模型、解决实际问题的方法和应用的思想方法.
1.实际问题:单摆问题、弹簧振子振动问题、交流电问题、温度变化问题等.
2.解三角函数应用题的基本步骤:
(1)审清题意;(2)收集整理数据,建立数学模型;(3)讨论变量关系,求解数学模型;(4)检验,作出结论.
3.思想方法:数形结合思想、数学建模思想.
设计意图:学生根据课堂学习,自主总结知识要点及运用的思想方法,让学生在总结过程中巩固本节课的知识和方法,内化知识,形成体系.
作 业
1.教材第201~202页练习第2,3,4题;教材第202~203页习题7.4第1,4,5,6题.
2.开放式作业:利用网络搜寻生活中还有哪些周而复始的现象?是否能用三角函数模型解决这类问题?以小组为单位,将查阅到的资料整理展示.
设计意图:巩固本节课学习的基本知识和基本方法,查漏补缺开放式作业可以培养学生收集信息、整理信息的能力和探究精神.
苏教版同步教材精品课件
7.4 三角函数应用
情境引入
既然大到宇宙天体的运动,小到质点的运动以及现实世界中具有周期性变化的现象无处不在,那么究竟怎样用三角函数解决这些具有周期性变化的问题?它到底能发挥哪些作用呢?
学生畅所欲言,将生活中、物理中的周而复始现象与三角函数建立关系.
设计意图:体会三角函数是解决周而复始现象的重要数学模型,体会三角函数在生活中的重要应用,学会利用数学的语言表达世界,培养学生的直观想象能力.
探究新知
问题1:(1)回忆从前所学,指数函数、对数函数以及幂函数的模型都是常用来描述现实世界中的哪些规律的?(2)数学模型是什么?建立数学模型的方法是什么?
(3)解决问题的一般步骤是什么?
(4)怎样处理收集到的数据?
师生互动,唤起回忆,充分复习前面学习过的建立数学模型的方法与过程对课前已经做好复习的学生给予表扬,并鼓励他们类比以前所学知识方法,继续探究新的数学模型.对还没有进入状态的学生,教师要帮助他们回忆并快速激起相应的知识方法:收集数据→画散点图→选择函数模型→求解函数模型→检验→用函数模型解释实际问题.
讨论结果:
(1)描述现实世界中不同增长规律的函数模型.
(2)简单地说,数学模型就是把实际问题用数学语言抽象概括,再从数学角度来反映或近似地反映实际问题时,所得出的关于实际问题的数学描述建立数学模型的方法就是把实际问题加以抽象概括,建立相应的数学模型,利用这些模型来研究实际问题的一般数学方法.
探究新知
(3)解决问题的一般步骤是:
①审题:逐字逐句阅读题意,审清楚题目条件、要求、理解数学关系;
②建模:分析题目变化趋势,选择适当的函数模型;
③求解:对所建立的数学模型进行分析研究得到数学结论;
④还原:把数学结论还原为实际问题的答案.
(4)画出散点图,分析它的变化趋势,确定合适的函数模型.
设计意图:引导学生回顾指数函数、对数函数以及幂函数模型的建立方法,为本节课的学习做好铺垫,让学生体会由实际问题建立三角函数模型的过程,培养和发展数学建模、数学抽象、直观想象等核心素养.
探究新知
问题2:如图,是单摆的示意图.点O为摆球的平衡位置,如果规定摆球向右偏移的位移为正,那么当摆球到达点C时,摆球的位移y达到最大值A;当摆球到达点O时,摆球的位移y为多少?当摆球到达点D时,摆球的位移y为多少?
教师通过多媒体展示单摆的动态过程,感受单摆的往复运动情况,在规定了正方向的情况下,学生很容易得到当摆球到达点O时,摆球的位移y为0;当摆球到达点D时,摆球的位移y为.
探究新知
教师再利用多媒体展示单摆随时间的位移变化图象的形成过程,让学生感受单摆的运动位移与时间的关系,理解单摆的位移与时间关系是模型.从而自然理解三角函数表达式中每一个量的物理意义:
x表示时间,y表示相对于平衡位置的偏离;
A表示物体运动时离开平衡位置的最大距离,称为振幅;
往复运动一次所需的时间称为这个运动的周期;
单位时间内往复运动的次数为运动的频率;
称为相位,时的相位称为初相位.
设计意图:感受三角函数在物理中的应用,理解简谐振动的图象是三角函数模型,掌握中每一个量的物理意义,同时培养学生的数学应用意识,感受数学与物理的密切联系,通过视频展示,培养学生的直观想象能力和逻辑推理能力,为下面的应用做好准备.
典例剖析
例1、在下图中,点O为做简谐运动的物体的平衡位置,取向右的方向为物体位移的正方向已知振幅为3cm周期为3s,且物体向右运动到距平衡位置最远处时开始计时求:
(1)设x和t之间的函数关系为.
则由,可得.
当时,有,即.
又,可得.
因此所求函数关系为,
即.
解析
(1)物体对平衡位置的位移x(单位:cm)和时间t(单位:s)之间的函数关系;
(2)该物体在s时的位置.
典例剖析
例1、在下图中,点O为做简谐运动的物体的平衡位置,取向右的方向为物体位移的正方向已知振幅为3cm周期为3s,且物体向右运动到距平衡位置最远处时开始计时求:
(2)令,得,故该物体在s时的位置是在O点的左侧且距O点1.5cm处.
解析
(1)物体对平衡位置的位移x(单位:cm)和时间t(单位:s)之间的函数关系;
(2)该物体在s时的位置.
设计意图:利用弹簧振子的振动,引入三角函数模型的建立过程,感受三角函数在物理中的广泛应用.
典例剖析
变式训练:一根长lcm的线,一端固定,另一端悬挂一个小球,小球摆动时离开平衡位置的位移s(cm)与时间t(s)的函数关系式是,其中g是重力加速度,当小球摆动的周期是1s时,线长 ( )
A. B. C. D.
单摆与弹簧振动一样,是简谐振动,其振动曲线是三角函数模型.因为周期,所以,则.
解析
D
典例剖析
例2、一半径为3m的水轮如图所示,水轮圆心O距离水面2m,已知水轮每分钟逆时针转动4圈,且当水轮上点P从水中浮现时(图中点)开始计算时间.
(1)如上图,建立平面直角坐标系.
设角是以为始边,为终边的角.
当OP在ts内所转过的角为,可知以为始边,OP为终边的角为,故P点纵坐标为,则.
当时,,可得,
因为,所以,故所求函数关系式为.
解析
(1)将点P到水面的距离z(单位:m在水面下,则z为负数)表示为时间t(单位:s)的函数;
(2)点P第一次到达最高点大约要多长时间?
典例剖析
例2、一半径为3m的水轮如图所示,水轮圆心O距离水面2m,已知水轮每分钟逆时针转动4圈,且当水轮上点P从水中浮现时(图中点)开始计算时间.
(2)令,得.
取,解得.
故点P第一次到达最高点大约需要5.5s.
解析
(1)将点P到水面的距离z(单位:m在水面下,则z为负数)表示为时间t(单位:s)的函数;
(2)点P第一次到达最高点大约要多长时间?
典例剖析
变式训练:某地一天的温度(单位:℃)随时间(单位:小时的变化近似满足函数关系:,且早上8时的温度为24℃.
(1)求函数的解析式,并判断这一天的最高温度是多少.出现在何时?
(2)当地有一通宵营业的超市,为了节省开支,规定在环境温度超过28℃时,开启中央空调降温,否则关闭中央空调,问中央空调应在何时开启?何时关闭?
(1)根据题意求出的值,确定函数的解析式利用正弦函数的图象与性质求得出现最高温时t的值;
(2)令,求出t的值即可得出结论.
分析
解析
(1),且早上8时的温度为24℃,即,
,解得.又时,.
.
又时,取得最大值,且,
令,解得,即这一天在14时(也是下午2时)出现最高温度,最高温度是32℃.
典例剖析
变式训练:某地一天的温度(单位:℃)随时间(单位:小时的变化近似满足函数关系:,且早上8时的温度为24℃.
(1)求函数的解析式,并判断这一天的最高温度是多少.出现在何时?
(2)当地有一通宵营业的超市,为了节省开支,规定在环境温度超过28℃时,开启中央空调降温,否则关闭中央空调,问中央空调应在何时开启?何时关闭?
(1)根据题意求出的值,确定函数的解析式利用正弦函数的图象与性质求得出现最高温时t的值;
(2)令,求出t的值即可得出结论.
分析
解析
(2)依题意知,令,可得.
,
或,解得或,即中央空调应在上午10时开启,下午18时(即下午6时)关闭.
设计意图:体会三角函数模型在生活中应用,巩固实际问题的解决方法和步骤.
典例剖析
例3、如图是某个弹簧振子(简称振子),它在完成一次全振动的过程中,时间t(单位:s)与位移y(单位:mm)之间的对应数据如下表所示.试根据这些数据确定这个振子的位移关于时间的函数解析式.
请你查阅资料,了解振子的运动原理解.
振子的振动具有循环往复的特点,由振子振动的物理学原理可知,其位移随时间的变化规律可以用函数来刻画.根据已知数据作出散点图,如图所示.
典例剖析
由数据表和散点图可知,振子振动时位移的最大值为20mm,因此;振子振动的周期为0.6s,即解得;再由初始状态()振子的位移为mm,可得,因此.所以这个振子的位移关于时间的函数解析式为.
典例剖析
归纳总结:现实生活中存在大量类似弹簧振子的运动,如钟摆的摆动,水中浮标的上下浮动,琴弦的振动,等等这些都是物体在某一中心位置附近循环往复的运动.在物理学中,把物体受到的力(总是指向平衡位置)正比于它离开平衡位置的距离的运动称为“简谐运动”.可以证明,在适当的直角坐标系下,简谐运动可以用函数表示,其中.描述简谐运动的物理量,如振幅、周期和频率等都与这个解析式中的常数有关:A就是这个简谐运动的振幅,它是做简谐运动的物体离开平衡位置的最大距离;这个简谐运动的周期是,它是做简谐运动的物体往复运动一次所需要的时间;这个简谐运动的频率由公式给出,它是做简谐运动的物体在单位时间内往复运动的次数;称为相位;时的相位称为初相位.
设计意图:通过对典型问题的分析解决,发展学生的数学建模、逻辑推理、直观想象、数学抽象、数学运算等核心素养.
典例剖析
变式训练:如图(1)所示的是某次实验测得的交变电流I(单位:A)随时间t(单位:s)变化的图象(频率为50Hz).将测得的图象放大,得到图(2).
(1)求电流I随时间t变化的函数解析式;
(2)当时,求电流I.
请你查阅资料,了解交变电流的产生原理.
解析
由交变电流的产生原理可知,电流I随时间t的变化规律可用来刻画,其中表示频率,A表示振幅,表示初相.
由图(2)可知,电流最大值为5A,因此;电流变化的周期为s,频率为50Hz,即,解得;再由初始状态()的电流约为4.33A,可得,因此约为.
所以电流Ⅰ随时间t变化的函数解析式是.
当时,;当时,;
当时,;当时,.
设计意图:感受三角函数模型在物理交流电中的应用,培养学生的数据分析能力和数学应用意识.
课堂小结
教师引导学生总结这节课学习的数学模型、解决实际问题的方法和应用的思想方法.
1.实际问题:单摆问题、弹簧振子振动问题、交流电问题、温度变化问题等.
2.解三角函数应用题的基本步骤:
(1)审清题意;(2)收集整理数据,建立数学模型;(3)讨论变量关系,求解数学模型;(4)检验,作出结论.
3.思想方法:数形结合思想、数学建模思想.
设计意图:学生根据课堂学习,自主总结知识要点及运用的思想方法,让学生在总结过程中巩固本节课的知识和方法,内化知识,形成体系.
作 业
1.教材第201~202页练习第2,3,4题;教材第202~203页习题7.4第1,4,5,6题.
2.开放式作业:利用网络搜寻生活中还有哪些周而复始的现象?是否能用三角函数模型解决这类问题?以小组为单位,将查阅到的资料整理展示.
设计意图:巩固本节课学习的基本知识和基本方法,查漏补缺开放式作业可以培养学生收集信息、整理信息的能力和探究精神.
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
