苏教版(2019)高中数学必修第一册 7.4 三角函数应用练习(解析版)
文档属性
| 名称 | 苏教版(2019)高中数学必修第一册 7.4 三角函数应用练习(解析版) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-22 00:00:00 | ||
图片预览




文档简介
7.4三角函数应用
教材知识梳理
三角函数模型的作用
三角函数作为描述现实世界中周期现象的一种数学模型,可以用来研究很多问题,在刻画周期变化规律、预测未来等方面发挥重要作用.
解三角函数应用问题的基本步骤
函数y=Asin(ωx+φ),A>0,ω>0中参数的物理意义
三角函数在物理中的应用
处理物理学问题的策略
(1)常涉及的物理学问题有单摆、光波、电流、机械波等,其共同的特点是具有周期性.
(2)明确物理概念的意义,此类问题往往涉及诸如频率、振幅等概念,因此要熟知其意义并与对应的三角函数知识结合解题.
例题研究
一、三角函数在生活中的应用
题型探究
例题1
为了研究钟表与三角函数的关系,建立如图所示的平面直角坐标系,设秒针针尖指向位置.若初始位置为,秒针从(注:此时)开始沿顺时针方向走动,则点的纵坐标与时间的函数关系式为( )
A. B.
C. D.
例题2
九章算术是我国古代著名数学经典其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小以锯锯之,深一寸,锯道长一尺问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示阴影部分为镶嵌在墙体内的部分已知弦尺,弓形高寸,估算该木材镶嵌在墙中的体积约为(注:1丈尺寸,,)
A.600立方寸 B.610立方寸 C.620立方寸 D.633立方寸
跟踪训练
训练1
某同学在做研究性学习时发现,在邢台大峡谷景区,每年到访的游客人数会发生周期性的变化.现假设该风景区每年各个月份游客的人数(单位:万人)可近似地用函数来刻画.其中:正整数表示月份且,例如时表示二月份;和是正整数;.统计发现,风景区每年各个月份游客人数有以下规律:
①每一年相同的月份,该风景区游客人数大致相同;
②该景区游客人数最多的八月份和最少的二月份相差约400000人;
③二月份该风景区游客大约为100000人,随后逐渐增加,八月份达到最多.
(1)试根据已知信息,确定一个符合条件的的表达式;
(2)一般地,当该地区游客超过400000人时,该风景区也进入了一年中的旅游“旺季”.那么,一年中的哪几个月是该风景区的旅游“旺季”?请说明理由.
训练2
平潭国际“花式风筝冲浪”集训队,在平潭龙凤头海滨浴场进行集训,海滨区域的某个观测点观测到该处水深(米)是随着一天的时间(,单位小时)呈周期性变化,某天各时刻的水深数据的近似值如下表:
(1)根据表中近似数据画出散点图(坐标系在答题卷中),观察散点图,选择一个合适的函数模型,并求 出该拟合模型的函数解析式;
(2)为保证队员安全,规定在一天中的时且水深不低于1.05米的时候进行训练,根据(1)中的选择的函数解析式,试问:这一天可以安排什么时间段组织训练,才能确保集训队员的安全.
二、几何中的三角函数模型
题型探究
例题1
如图,“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设大正方形的面积为,小正方形的面积为,且,则( )
A. B.
C.2 D.3
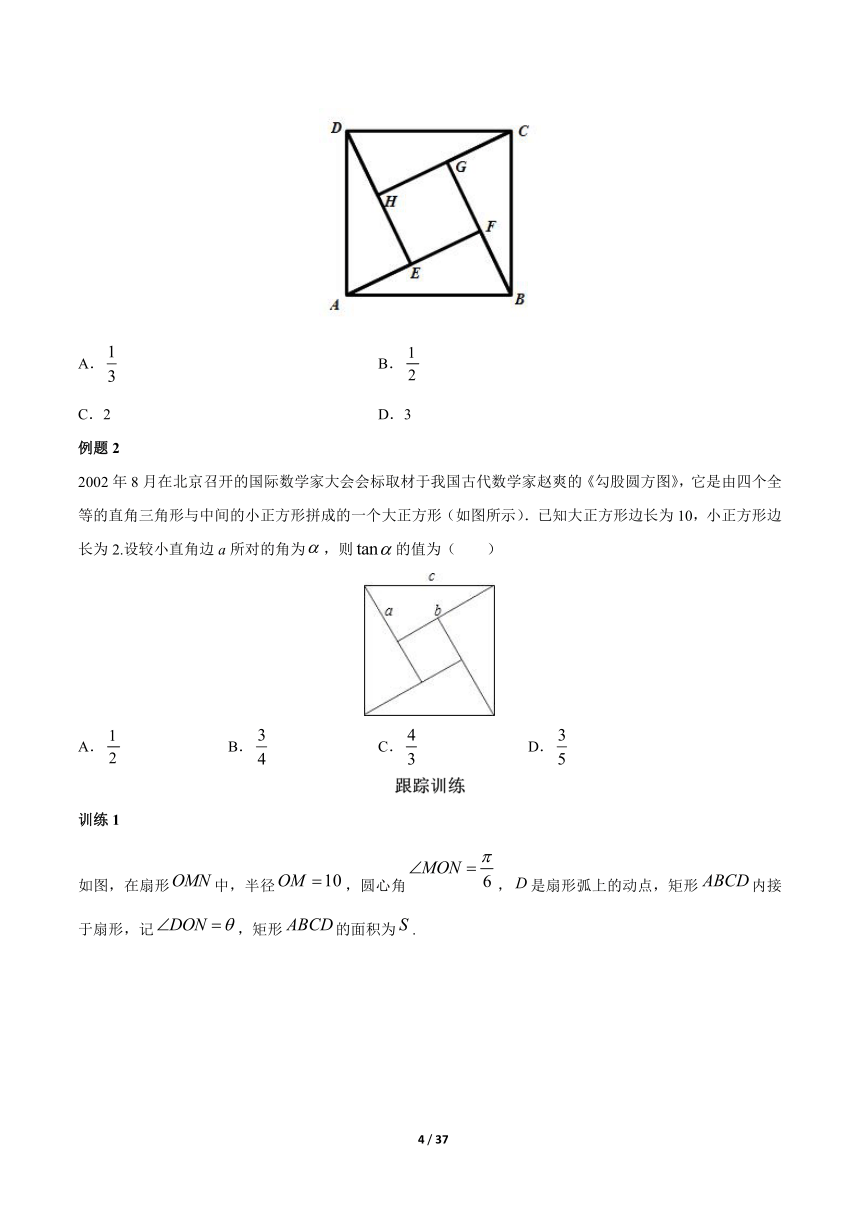
例题2
2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图所示).已知大正方形边长为10,小正方形边长为2.设较小直角边a所对的角为,则的值为( )
A. B. C. D.
跟踪训练
训练1
如图,在扇形中,半径,圆心角,是扇形弧上的动点,矩形内接于扇形,记,矩形的面积为.
(1)用含的式子表示线段,的长;
(2)求的最大值.
训练2
如图,已知中,.设,,它的内接正方形的一边在斜边上,、分别在、上.假设的面积为,正方形的面积为.
(Ⅰ)用表示的面积和正方形的面积;
(Ⅱ)设,试求的最大值,并判断此时的形状.
综合式测试
一、单选题
1.某地市委、市政府坚持创新、协调、绿色、开放、共享的发展理念,把高质量发展同满足人民美好生活需要紧密结合起来,坚持生态优先.下图是该市某公园三期规划的一角示意图.边长为3百米的正方形花圃的中,建有是以为圆心,1百米为半径的扇形水池,现需在其余部分设计一个矩形草坪,其中是水池边上任意一点,点,分别在边和上,则规划中矩形草坪面积的最小值为( )平方百米.
A. B. C.4 D.6
2.如图,一个摩天轮的半径为10m,轮子的最低处距离地面2m.如果此摩天轮按逆时针匀速转动,每30分钟转一圈,且当摩天轮上某人经过点(点与摩天轮天轮中心的高度相同)时开始计时,在摩天轮转动的一圈内,此人相对于地面的高度不小于17m的时间大约是( )
A.8分钟 B.10分钟 C.12分钟 D.14分钟
3.函数,若,则的最小值是( )
A. B. C. D.
4.一观览车的主架示意图如图所示,其中为轮轴的中心,距地面(即长),巨轮的半径长为,,巨轮逆时针旋转且每分钟转一圈,若点为吊舱的初始位置,经过分钟,该吊舱距离地面的高度为( )
A. B.
C. D.
5.为迎接大运会的到来,学校决定在半径为,圆心角为的扇形空地的内部修建一平行四边形观赛场地,如图所示.则观赛场地的面积最大值为( )
A. B.
C. D.
6.如图所示,秒针尖的位置为,若初始位置为,当秒针从(此时)正常开始走时,那么点M的横坐标与时间t的函数关系为( )
A. B.
C. D.
7.动点在圆上绕坐标原点沿逆时针方向匀速旋转,其初始位置为,12秒旋转一周,则动点的纵坐标关于时间(单位:秒)的函数式为( )
A. B.
C. D.
8.车流量被定义为单位时间内通过十字路口的车辆数,单位为辆/分钟.若上班高峰期某十字路口的车流量(单位:辆/分钟)与时间(单位:分钟)的函数关系式为,则下列哪个时间段内车流量是增加的( )
A. B. C. D.
二、填空题
9.哈尔滨文化公园的摩天轮始建于2003年1月15日,2003年4月30日竣工,是当时中国第一高的巨型摩天轮,其旋转半径50米,最高点距地地面110米,运行一周大约21分钟.某人在最低点的位置坐上摩天轮,则第14分钟时他距地面大约为__米.
10.如图,以正方形的各边为底可向外作四个腰长为1的等腰三角形,则阴影部分面积的最大值是___________.
11.如图,游乐场所的摩天轮匀速旋转,每转一周需要l2min,其中心O离地面45米,半径40米.如果你从最低处登上摩天轮,那么你与地面的距离将随时间的变化而变化,以你登上摩天轮的时刻开始计时,请问:当你第六次距离地面65米时,用了________分钟?
12.如图,货轮在海上以的速度沿着方位角(从指北方向顺时针转到目标方向线的水平角)为150°的方向航行.为了确定船位,在点B观察灯塔A的方位角是120°,航行半小时后到达C点,观察灯塔A的方位角是75°,则货轮到达C点时与灯塔A的距离为______ n mile
三、解答题
13.现有一块半径为,圆心角为的扇形铁皮废料,现在准备利用这块铁皮制作一些图形模型.已知点P在弧上,设.
图1 图2
(1)方案1:过点P裁剪一个扇形内接矩形(如图1),点Q在上,点M,N在上,
①若,求矩形的面积;
②若矩形是正方形,求的值;
(2)方案2:从P点处分别向作两条垂线和,垂足为S,T,(如图2)这样可以裁剪出两个直角三角形和,为了提高废料的利用率,我们希望这两个直角三角形面积和最大,试问此时点P应在何处?请说明你的理由.
14.圣·索菲亚教堂(SAINT SOPHIA CATHEDRAL)是一座始建于1907年拜占庭风格的东正教教堂,为哈尔滨的标志性建筑,1996年经国务院批准,被列为第四批全国重点文物保护单位,是每一位到哈尔滨旅游的游客拍照打卡的必到景点,其中央主体建筑集球、圆柱、棱柱于一体,极具对称之美,可以让游客从任何角度都能领略它的美,如左图.某校高一数学兴趣小组打算根据所学知识估算索菲亚教堂的高度,他们在索菲亚教堂的正东方向找到一座建筑物,测得建筑物的高度为h,在它们之间的地面上的点M(B,M,D三点共线)处可以测得楼顶A和教堂顶C的仰角分别为和,在楼顶A处可测得塔顶C的仰角为,且与都垂直地面,如右图,那么请你根据他们测得的数据估算索菲亚教堂的高度为多少?(结果用h,,,表示)
15.如图,直角坐标系建立在湖泊的某一恰当位置,现准备在湖泊的一侧修建一条观光大道,它的前一段是以为圆心,为半径的圆弧,后一段是函数,时的图像,图像的最高点为.
(1)求函数的解析式;
(2)若在湖泊内修建如图的矩形水上乐园,其中折线为水上赛艇线路,问点落在圆弧上何处时赛艇线路最长?
7.4三角函数应用答案解析
教材知识梳理
三角函数模型的作用
三角函数作为描述现实世界中周期现象的一种数学模型,可以用来研究很多问题,在刻画周期变化规律、预测未来等方面发挥重要作用.
解三角函数应用问题的基本步骤
函数y=Asin(ωx+φ),A>0,ω>0中参数的物理意义
三角函数在物理中的应用
处理物理学问题的策略
(1)常涉及的物理学问题有单摆、光波、电流、机械波等,其共同的特点是具有周期性.
(2)明确物理概念的意义,此类问题往往涉及诸如频率、振幅等概念,因此要熟知其意义并与对应的三角函数知识结合解题.
例题研究
一、三角函数在生活中的应用
题型探究
例题1
为了研究钟表与三角函数的关系,建立如图所示的平面直角坐标系,设秒针针尖指向位置.若初始位置为,秒针从(注:此时)开始沿顺时针方向走动,则点的纵坐标与时间的函数关系式为( )
A. B.
C. D.
【答案】C
【分析】根据条件先确定周期从而求解出的值,设出与时间的函数关系式(注意秒针是顺时针方向转动),根据初始位置计算出的值从而求解出关系式.
【详解】
由题意,函数的周期为,∴.
设函数解析式为(秒针是顺时针走动).
∵初始位置为,∴时,.∴,可取.
∴函数的解析式为.
故选C.
【点睛】考查利用三角函数的实际模型求解函数解析式
例题2
九章算术是我国古代著名数学经典其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小以锯锯之,深一寸,锯道长一尺问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示阴影部分为镶嵌在墙体内的部分已知弦尺,弓形高寸,估算该木材镶嵌在墙中的体积约为(注:1丈尺寸,,)
A.600立方寸 B.610立方寸 C.620立方寸 D.633立方寸
【答案】D
【分析】由三角形,利用勾股定理可得半径,进而得,再利用,乘以高即可得体积.
【详解】
连接,设⊙的半径为,
则,所以.
由于,
所以,即.
所以 平方寸.
∴该木材镶嵌在墙中的体积为立方寸,
故选D.
【点睛】考查了垂径定理和勾股定理及扇形的面积公式,柱体的体积公式,属于中档题
跟踪训练
训练1
某同学在做研究性学习时发现,在邢台大峡谷景区,每年到访的游客人数会发生周期性的变化.现假设该风景区每年各个月份游客的人数(单位:万人)可近似地用函数来刻画.其中:正整数表示月份且,例如时表示二月份;和是正整数;.统计发现,风景区每年各个月份游客人数有以下规律:
①每一年相同的月份,该风景区游客人数大致相同;
②该景区游客人数最多的八月份和最少的二月份相差约400000人;
③二月份该风景区游客大约为100000人,随后逐渐增加,八月份达到最多.
(1)试根据已知信息,确定一个符合条件的的表达式;
(2)一般地,当该地区游客超过400000人时,该风景区也进入了一年中的旅游“旺季”.那么,一年中的哪几个月是该风景区的旅游“旺季”?请说明理由.
【答案】(1);(2)一年中的7,8,9,10四个月是该风景区的旅游“旺季”,理由见解析.
【分析】
(1)由实际问题的周期性且周期为、淡旺季数据,结合数学模型即可求,,进而可得表达式;
(2)由(1)结合已知条件即可求出的范围,结合实际条件即可知旺季所含月份.
【详解】
(1)根据三条规律,可知该函数为周期函数且周期为12,可得,即,
由规律②③可知,,解得:,
综上可得,;
(2)由条件,,可得
∴,,即,
又,,所以,,故:,8,9,10,
即一年中的7,8,9,10四个月是该风景区的旅游“旺季”.
【点睛】考查了三角函数的实际应用.
训练2
平潭国际“花式风筝冲浪”集训队,在平潭龙凤头海滨浴场进行集训,海滨区域的某个观测点观测到该处水深(米)是随着一天的时间(,单位小时)呈周期性变化,某天各时刻的水深数据的近似值如下表:
(1)根据表中近似数据画出散点图(坐标系在答题卷中),观察散点图,选择一个合适的函数模型,并求 出该拟合模型的函数解析式;
(2)为保证队员安全,规定在一天中的时且水深不低于1.05米的时候进行训练,根据(1)中的选择的函数解析式,试问:这一天可以安排什么时间段组织训练,才能确保集训队员的安全.
【答案】(1)(2)这一天可以安排早上5点至7点以及11点至18点的时间段组织训练, 才能确保集训队员的安全.
【解析】
分析:(1)根据表中近似数据画出散点图,选做为函数模型,由此利用三角函数的图象和性质能求出该拟合模型的函数解析式.
(2)由(1)知:,令,即,从而,由此能求出这一天可以安排早上5点至7点以及11点至18点的时间段组织训练,才能确保集训队员的安全.
详解:
(1)根据表中近似数据画出散点图,如图所示:
依题意,选做为函数模型,
∴
∵ ∴
∴
又∵函数的图象过点
∴,∴
∴.
(2)由(1)知:
令,即
∴
∴
∴
又∵
∵或
∴这一天可以安排早上5点至7点以及11点至18点的时间段组织训练, 才能确保集训队员的安全.
二、几何中的三角函数模型
题型探究
例题1
如图,“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设大正方形的面积为,小正方形的面积为,且,则( )
A. B.
C.2 D.3
【答案】B
【分析】设大正方形的边长为,则由已知条件可得小正方形的边长为,设为,在在中,由勾股定理得, ,可求得,所以
【详解】
解:设大正方形的边长为,
因为,所以,得,
所以小正方形的边长为,
所以,
设为,则,
在中,由勾股定理得,
所以,
解得或(舍去),
所以
故选:B
例题2
2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图所示).已知大正方形边长为10,小正方形边长为2.设较小直角边a所对的角为,则的值为( )
A. B. C. D.
【答案】B
【分析】由题意可知,利用勾股定理可求出,从而可求出的值.
【详解】
由题意可得,所以,
解得或(舍去),故,
所以,
故选:B
【点睛】考查了勾股定理的应用
跟踪训练
训练1
如图,在扇形中,半径,圆心角,是扇形弧上的动点,矩形内接于扇形,记,矩形的面积为.
(1)用含的式子表示线段,的长;
(2)求的最大值.
【答案】(1),;,;(2).
【分析】
(1)在和中利用三角函数的定义可表示出;
(2)求出后可得矩形面积,利用二倍角公式,两角和的正弦公式化函数为一个角的一个三角函数形式,然后由正弦函数性质可得最大值.
【详解】
解:(1)在中,,∴,,
又中,,,
∴,;
(2)在中,,∴,
∴
,
∵,∴,
∴当即时,.
【点睛】考查三角函数的应用,解题关键是用角表示出矩形面积,然后可利用三角函数的恒等变换公式如二倍角公式、两角和与差的正弦(余弦)公式、诱导公式等化函数为一个角的一个三角函数形式,即形式,最后利用正弦函数性质求得结论.
训练2
如图,已知中,.设,,它的内接正方形的一边在斜边上,、分别在、上.假设的面积为,正方形的面积为.
(Ⅰ)用表示的面积和正方形的面积;
(Ⅱ)设,试求的最大值,并判断此时的形状.
【答案】(Ⅰ),;,(Ⅱ)最大值为;为等腰直角三角形
【分析】
(Ⅰ)根据直角三角形,底面积乘高是面积;然后考虑正方形的边长,求出边长之后,即可表示正方形面积;
(Ⅱ)化简的表达式,利用基本不等式求最值,注意取等号的条件.
【详解】
解:(Ⅰ)∵在中,∴,. ∴
∴,
设正方形边长为,则,,
∴.
∴,
∴,
(Ⅱ)解:由(Ⅰ)可得
,
令,
∵在区间上是减函数
∴当时,取得最小值, 即取得最大值.
∴的最大值为
此时
∴为等腰直角三角形
【点睛】(1)函数的实际问题中,不仅要根据条件列出函数解析式时,同时还要注意定义域;
(2)求解函数的最值的时候,当取到最值时,一定要添加增加取等号的条件.
综合式测试
一、单选题
1.某地市委、市政府坚持创新、协调、绿色、开放、共享的发展理念,把高质量发展同满足人民美好生活需要紧密结合起来,坚持生态优先.下图是该市某公园三期规划的一角示意图.边长为3百米的正方形花圃的中,建有是以为圆心,1百米为半径的扇形水池,现需在其余部分设计一个矩形草坪,其中是水池边上任意一点,点,分别在边和上,则规划中矩形草坪面积的最小值为( )平方百米.
A. B. C.4 D.6
【答案】B
【分析】设∠PAB=θ,过P作PE垂直AB于点E,进而用表示出了矩形PNCQ的边长,即可解出.
【详解】
,设,过P作PE垂直AB于点E,如图:
,
时,面积有最小值,
故选:B
2.如图,一个摩天轮的半径为10m,轮子的最低处距离地面2m.如果此摩天轮按逆时针匀速转动,每30分钟转一圈,且当摩天轮上某人经过点(点与摩天轮天轮中心的高度相同)时开始计时,在摩天轮转动的一圈内,此人相对于地面的高度不小于17m的时间大约是( )
A.8分钟 B.10分钟 C.12分钟 D.14分钟
【答案】B
【分析】由题可得此人相对于地面的高度与时间的关系是,再令求出的范围即可得出.
【详解】
设时间为时,此人相对于地面的高度为,
则由题可得当时,,
在时间时,此人转过的角为,
此时此人相对于地面的高度,
令,则,
所以,解得,
故在摩天轮转动的一圈内,此人相对于地面的高度不小于17m的时间大约是.
故选:B.
【点睛】考查三角函数的实际应用,解题的关键是得出高度与时间的关系,再解三角函数不等式即可.
3.函数,若,则的最小值是( )
A. B. C. D.
【答案】A
【分析】化简得,由可知在,处取到最大值和最小值,不妨设在处有最大值,处取到最小值,可得,,,即可求出的最小值.
【详解】
,
∴函数的最大值为3,最小值为﹣1,
又,∴在,处取到最大值和最小值,
不妨设在处有最大值,则,即,
处取到最小值,则,即,
所以,,,
所以当时,的最小值为.
【点睛】
结论点睛:正弦型函数最值:
① ,当, 时取最大值;
②,当, 时取最小值.
4.一观览车的主架示意图如图所示,其中为轮轴的中心,距地面(即长),巨轮的半径长为,,巨轮逆时针旋转且每分钟转一圈,若点为吊舱的初始位置,经过分钟,该吊舱距离地面的高度为( )
A. B.
C. D.
【答案】B
【分析】
先通过计算得出转动的角速度,然后利用三角函数模型表示在转动的过程中点的纵坐标满足的关系式,则吊舱到底面的距离为点的纵坐标减.
【详解】
如图所示,以点为坐标原点,以水平方向为轴,以所在直线为轴建立平面直角坐标系.
因为巨轮逆时针旋转且每分钟转一圈,则转动的角速度为每分钟,
经过分钟之后,转过的角度为,
所以,在转动的过程中,点的纵坐标满足:
则吊舱距离地面的距离.
故选:B.
【点睛】
建立三角函数模型解决实际问题的一般步骤:
(1)审题:审清楚题目条件、要求、理解数学关系;
(2)建模:分析题目变化趋势,选择合适的三角函数模型;
(3)求解:对所建立的数学模型进行分析研究,从而得到结论.
5.为迎接大运会的到来,学校决定在半径为,圆心角为的扇形空地的内部修建一平行四边形观赛场地,如图所示.则观赛场地的面积最大值为( )
A. B.
C. D.
【答案】D
【分析】
如图,连接,设,可用的三角函数值表示,,即可得到四边形的面积,再根据三角函数的值域的求法即可求解.
【详解】
如图所示: .
连接,设,作,,垂足分别为.
根据平面几何知识可知,,,.
∴,.
故四边形的面积也为四边形的面积,
即有
,其中.
所以当即时,.
故选:D.
【点睛】考查利用三角函数解决几何中的最值问题,意在考查学生的数学建模能力和数学运算能力,属于基础题.
6.如图所示,秒针尖的位置为,若初始位置为,当秒针从(此时)正常开始走时,那么点M的横坐标与时间t的函数关系为( )
A. B.
C. D.
【答案】C
【分析】
根据条件先确定周期从而求解出的值,设出与时间的函数关系式(注意秒针是顺时针方向转动),根据初始位置,计算出的值从而求解出关系式.
【详解】
初始角为,周期,所以,,
设与时间的函数关系式(因为秒针是顺时针走动)
所以,当秒针运动到M点时,.
故选:C.
【点睛】考查利用三角函数的实际模型求解函数解析式,难度一般.钟表问题的三角函数实际模型中,由于分针、时针、秒针都是顺时针转动,因此在确定的时候要注意取负值,这里依据的是角的正负的定义.
7.动点在圆上绕坐标原点沿逆时针方向匀速旋转,其初始位置为,12秒旋转一周,则动点的纵坐标关于时间(单位:秒)的函数式为( )
A. B.
C. D.
【答案】C
【分析】设关于的函数:,根据周期求出,再根据过点求出,问题得以解决.
【详解】
设关于的函数:
动点12秒旋转一周,则 ,得.
动点的初始位置为.
即时,,即,则可取
所以
故选:C
【点睛】考查函数的解析式的求法,体现了转化的数学思想,属于中档题.
8.车流量被定义为单位时间内通过十字路口的车辆数,单位为辆/分钟.若上班高峰期某十字路口的车流量(单位:辆/分钟)与时间(单位:分钟)的函数关系式为,则下列哪个时间段内车流量是增加的( )
A. B. C. D.
【答案】C
【分析】
由题意可知,问题是求函数在上的单调递增区间的子集,即先求出该函数在上的增区间,与取交集,并判断每个选项中的区间与单调增区间的包含关系即可得出合适选项.
【详解】
令,.
,当时,函数的单调递增区间为,当时,函数的单调递增区间为.
,车流量在时间段内是增加的,
故选:C.
【点睛】考查三角函数的实际应用,将问题转化为三角函数的单调性是解答的关键,考查分析问题和解决问题的能力,属于中等题.
二、填空题
9.哈尔滨文化公园的摩天轮始建于2003年1月15日,2003年4月30日竣工,是当时中国第一高的巨型摩天轮,其旋转半径50米,最高点距地地面110米,运行一周大约21分钟.某人在最低点的位置坐上摩天轮,则第14分钟时他距地面大约为__米.
【答案】85
【分析】
设与地面高度与时间的关系,,,,,根据已知求出,即得解.
【详解】
设与地面高度与时间的关系,,,,,
由题意可知:,,,,
即,
又因为,即,故,,
所以第14分钟时他距地面大约为.
故答案为:85.
【点睛】方法点睛:求三角函数的解析式,通常用待定系数法,先定式(设出三角函数的解析式),再定量(解方程组求出待定系数).
10.如图,以正方形的各边为底可向外作四个腰长为1的等腰三角形,则阴影部分面积的最大值是___________.
【答案】
【分析】
设等腰三角形底角为,阴影面积为,根据正弦函数的图象与性质即可得到结果.
【详解】
设等腰三角形底角为,则等腰三角形底边长为高为,
阴影面积为:
,
当时,阴影面积的最大值为
故答案为
【点睛】考查平面图形的面积问题,考查三角函数的图象与性质,解题关键用等腰三角形底角为表示等腰三角形的底边与高.
11.如图,游乐场所的摩天轮匀速旋转,每转一周需要l2min,其中心O离地面45米,半径40米.如果你从最低处登上摩天轮,那么你与地面的距离将随时间的变化而变化,以你登上摩天轮的时刻开始计时,请问:当你第六次距离地面65米时,用了________分钟?
【答案】32.
【分析】
根据题意得到,化简得到或,得到答案.
【详解】
设时间为,,根据题意:,故.
故或,故或,.
故.
故答案为:.
【点睛】考查了三角函数的应用,意在考查学生的应用能力.
12.如图,货轮在海上以的速度沿着方位角(从指北方向顺时针转到目标方向线的水平角)为150°的方向航行.为了确定船位,在点B观察灯塔A的方位角是120°,航行半小时后到达C点,观察灯塔A的方位角是75°,则货轮到达C点时与灯塔A的距离为______ n mile
【答案】
【分析】
通过方位角定义,求出,,利用正弦定理即可得到答案.
【详解】
根据题意,可知,,,因此可得,由正弦定理得:,求得,即答案为.
【点睛】考查正弦定理的实际应用,难度不大.
三、解答题
13.现有一块半径为,圆心角为的扇形铁皮废料,现在准备利用这块铁皮制作一些图形模型.已知点P在弧上,设.
图1 图2
(1)方案1:过点P裁剪一个扇形内接矩形(如图1),点Q在上,点M,N在上,
①若,求矩形的面积;
②若矩形是正方形,求的值;
(2)方案2:从P点处分别向作两条垂线和,垂足为S,T,(如图2)这样可以裁剪出两个直角三角形和,为了提高废料的利用率,我们希望这两个直角三角形面积和最大,试问此时点P应在何处?请说明你的理由.
【答案】(1)①,②;(2)点为的中点.
【分析】
(1)①由题意可用表示出,即可求出矩形的面积;
②在中,直接表示出角的正切,即可得到结果;
(2)将两个三角形的面积和表示出来,然后利用三角函数知识即可求解.
【详解】
(1)①因为,所以,因为,所以,则,所以,故;
②设,在中,,所以,在中,;
(2)因为,所以,
所以
,
当,即 ,所以时,即点为的中点时,这两个直角三角形面积和最大,
14.圣·索菲亚教堂(SAINT SOPHIA CATHEDRAL)是一座始建于1907年拜占庭风格的东正教教堂,为哈尔滨的标志性建筑,1996年经国务院批准,被列为第四批全国重点文物保护单位,是每一位到哈尔滨旅游的游客拍照打卡的必到景点,其中央主体建筑集球、圆柱、棱柱于一体,极具对称之美,可以让游客从任何角度都能领略它的美,如左图.某校高一数学兴趣小组打算根据所学知识估算索菲亚教堂的高度,他们在索菲亚教堂的正东方向找到一座建筑物,测得建筑物的高度为h,在它们之间的地面上的点M(B,M,D三点共线)处可以测得楼顶A和教堂顶C的仰角分别为和,在楼顶A处可测得塔顶C的仰角为,且与都垂直地面,如右图,那么请你根据他们测得的数据估算索菲亚教堂的高度为多少?(结果用h,,,表示)
【答案】高度为.
【分析】
设,首先根据题目示意图,分析得到,,,,最后在中利用正弦定理得到求解.
【详解】
解:由题可知,在中,,
设,
则,
在中,,
则.
在中,
∴
由正弦定理可知
,
即.
∴
答:索菲亚教堂的高度为.
【点睛】解三角形应用题的一般步骤:
(1)阅读理解题意,弄清问题的实际背景,明确已知与未知,理清量与量之间的关系.
(2)根据题意画出示意图,将实际问题抽象成解三角形问题的模型.
(3)根据题意选择正弦定理或余弦定理求解.
(4)将三角形问题还原为实际问题,注意实际问题中的有关单位问题、近似计算的要求等.
15.如图,直角坐标系建立在湖泊的某一恰当位置,现准备在湖泊的一侧修建一条观光大道,它的前一段是以为圆心,为半径的圆弧,后一段是函数,时的图像,图像的最高点为.
(1)求函数的解析式;
(2)若在湖泊内修建如图的矩形水上乐园,其中折线为水上赛艇线路,问点落在圆弧上何处时赛艇线路最长?
【答案】(1),;(2)当点坐标为时赛艇线路最长.
【分析】
(1)由图可知,,即可求出,将代入可求;
(2)求出的坐标,连接,设,将赛艇线路长表示为关于的三角函数形式,即可根据三角函数性质求解.
【详解】
(1)由图象知,,即,则,
将代入,则,
则,又,,
所以,;
(2)在中令,得,∴.
连接,设,,则.
设赛艇线路长为,则,
当时,有最大值,此时.
所以当点坐标为时赛艇线路最长.
10 / 37
教材知识梳理
三角函数模型的作用
三角函数作为描述现实世界中周期现象的一种数学模型,可以用来研究很多问题,在刻画周期变化规律、预测未来等方面发挥重要作用.
解三角函数应用问题的基本步骤
函数y=Asin(ωx+φ),A>0,ω>0中参数的物理意义
三角函数在物理中的应用
处理物理学问题的策略
(1)常涉及的物理学问题有单摆、光波、电流、机械波等,其共同的特点是具有周期性.
(2)明确物理概念的意义,此类问题往往涉及诸如频率、振幅等概念,因此要熟知其意义并与对应的三角函数知识结合解题.
例题研究
一、三角函数在生活中的应用
题型探究
例题1
为了研究钟表与三角函数的关系,建立如图所示的平面直角坐标系,设秒针针尖指向位置.若初始位置为,秒针从(注:此时)开始沿顺时针方向走动,则点的纵坐标与时间的函数关系式为( )
A. B.
C. D.
例题2
九章算术是我国古代著名数学经典其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小以锯锯之,深一寸,锯道长一尺问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示阴影部分为镶嵌在墙体内的部分已知弦尺,弓形高寸,估算该木材镶嵌在墙中的体积约为(注:1丈尺寸,,)
A.600立方寸 B.610立方寸 C.620立方寸 D.633立方寸
跟踪训练
训练1
某同学在做研究性学习时发现,在邢台大峡谷景区,每年到访的游客人数会发生周期性的变化.现假设该风景区每年各个月份游客的人数(单位:万人)可近似地用函数来刻画.其中:正整数表示月份且,例如时表示二月份;和是正整数;.统计发现,风景区每年各个月份游客人数有以下规律:
①每一年相同的月份,该风景区游客人数大致相同;
②该景区游客人数最多的八月份和最少的二月份相差约400000人;
③二月份该风景区游客大约为100000人,随后逐渐增加,八月份达到最多.
(1)试根据已知信息,确定一个符合条件的的表达式;
(2)一般地,当该地区游客超过400000人时,该风景区也进入了一年中的旅游“旺季”.那么,一年中的哪几个月是该风景区的旅游“旺季”?请说明理由.
训练2
平潭国际“花式风筝冲浪”集训队,在平潭龙凤头海滨浴场进行集训,海滨区域的某个观测点观测到该处水深(米)是随着一天的时间(,单位小时)呈周期性变化,某天各时刻的水深数据的近似值如下表:
(1)根据表中近似数据画出散点图(坐标系在答题卷中),观察散点图,选择一个合适的函数模型,并求 出该拟合模型的函数解析式;
(2)为保证队员安全,规定在一天中的时且水深不低于1.05米的时候进行训练,根据(1)中的选择的函数解析式,试问:这一天可以安排什么时间段组织训练,才能确保集训队员的安全.
二、几何中的三角函数模型
题型探究
例题1
如图,“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设大正方形的面积为,小正方形的面积为,且,则( )
A. B.
C.2 D.3
例题2
2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图所示).已知大正方形边长为10,小正方形边长为2.设较小直角边a所对的角为,则的值为( )
A. B. C. D.
跟踪训练
训练1
如图,在扇形中,半径,圆心角,是扇形弧上的动点,矩形内接于扇形,记,矩形的面积为.
(1)用含的式子表示线段,的长;
(2)求的最大值.
训练2
如图,已知中,.设,,它的内接正方形的一边在斜边上,、分别在、上.假设的面积为,正方形的面积为.
(Ⅰ)用表示的面积和正方形的面积;
(Ⅱ)设,试求的最大值,并判断此时的形状.
综合式测试
一、单选题
1.某地市委、市政府坚持创新、协调、绿色、开放、共享的发展理念,把高质量发展同满足人民美好生活需要紧密结合起来,坚持生态优先.下图是该市某公园三期规划的一角示意图.边长为3百米的正方形花圃的中,建有是以为圆心,1百米为半径的扇形水池,现需在其余部分设计一个矩形草坪,其中是水池边上任意一点,点,分别在边和上,则规划中矩形草坪面积的最小值为( )平方百米.
A. B. C.4 D.6
2.如图,一个摩天轮的半径为10m,轮子的最低处距离地面2m.如果此摩天轮按逆时针匀速转动,每30分钟转一圈,且当摩天轮上某人经过点(点与摩天轮天轮中心的高度相同)时开始计时,在摩天轮转动的一圈内,此人相对于地面的高度不小于17m的时间大约是( )
A.8分钟 B.10分钟 C.12分钟 D.14分钟
3.函数,若,则的最小值是( )
A. B. C. D.
4.一观览车的主架示意图如图所示,其中为轮轴的中心,距地面(即长),巨轮的半径长为,,巨轮逆时针旋转且每分钟转一圈,若点为吊舱的初始位置,经过分钟,该吊舱距离地面的高度为( )
A. B.
C. D.
5.为迎接大运会的到来,学校决定在半径为,圆心角为的扇形空地的内部修建一平行四边形观赛场地,如图所示.则观赛场地的面积最大值为( )
A. B.
C. D.
6.如图所示,秒针尖的位置为,若初始位置为,当秒针从(此时)正常开始走时,那么点M的横坐标与时间t的函数关系为( )
A. B.
C. D.
7.动点在圆上绕坐标原点沿逆时针方向匀速旋转,其初始位置为,12秒旋转一周,则动点的纵坐标关于时间(单位:秒)的函数式为( )
A. B.
C. D.
8.车流量被定义为单位时间内通过十字路口的车辆数,单位为辆/分钟.若上班高峰期某十字路口的车流量(单位:辆/分钟)与时间(单位:分钟)的函数关系式为,则下列哪个时间段内车流量是增加的( )
A. B. C. D.
二、填空题
9.哈尔滨文化公园的摩天轮始建于2003年1月15日,2003年4月30日竣工,是当时中国第一高的巨型摩天轮,其旋转半径50米,最高点距地地面110米,运行一周大约21分钟.某人在最低点的位置坐上摩天轮,则第14分钟时他距地面大约为__米.
10.如图,以正方形的各边为底可向外作四个腰长为1的等腰三角形,则阴影部分面积的最大值是___________.
11.如图,游乐场所的摩天轮匀速旋转,每转一周需要l2min,其中心O离地面45米,半径40米.如果你从最低处登上摩天轮,那么你与地面的距离将随时间的变化而变化,以你登上摩天轮的时刻开始计时,请问:当你第六次距离地面65米时,用了________分钟?
12.如图,货轮在海上以的速度沿着方位角(从指北方向顺时针转到目标方向线的水平角)为150°的方向航行.为了确定船位,在点B观察灯塔A的方位角是120°,航行半小时后到达C点,观察灯塔A的方位角是75°,则货轮到达C点时与灯塔A的距离为______ n mile
三、解答题
13.现有一块半径为,圆心角为的扇形铁皮废料,现在准备利用这块铁皮制作一些图形模型.已知点P在弧上,设.
图1 图2
(1)方案1:过点P裁剪一个扇形内接矩形(如图1),点Q在上,点M,N在上,
①若,求矩形的面积;
②若矩形是正方形,求的值;
(2)方案2:从P点处分别向作两条垂线和,垂足为S,T,(如图2)这样可以裁剪出两个直角三角形和,为了提高废料的利用率,我们希望这两个直角三角形面积和最大,试问此时点P应在何处?请说明你的理由.
14.圣·索菲亚教堂(SAINT SOPHIA CATHEDRAL)是一座始建于1907年拜占庭风格的东正教教堂,为哈尔滨的标志性建筑,1996年经国务院批准,被列为第四批全国重点文物保护单位,是每一位到哈尔滨旅游的游客拍照打卡的必到景点,其中央主体建筑集球、圆柱、棱柱于一体,极具对称之美,可以让游客从任何角度都能领略它的美,如左图.某校高一数学兴趣小组打算根据所学知识估算索菲亚教堂的高度,他们在索菲亚教堂的正东方向找到一座建筑物,测得建筑物的高度为h,在它们之间的地面上的点M(B,M,D三点共线)处可以测得楼顶A和教堂顶C的仰角分别为和,在楼顶A处可测得塔顶C的仰角为,且与都垂直地面,如右图,那么请你根据他们测得的数据估算索菲亚教堂的高度为多少?(结果用h,,,表示)
15.如图,直角坐标系建立在湖泊的某一恰当位置,现准备在湖泊的一侧修建一条观光大道,它的前一段是以为圆心,为半径的圆弧,后一段是函数,时的图像,图像的最高点为.
(1)求函数的解析式;
(2)若在湖泊内修建如图的矩形水上乐园,其中折线为水上赛艇线路,问点落在圆弧上何处时赛艇线路最长?
7.4三角函数应用答案解析
教材知识梳理
三角函数模型的作用
三角函数作为描述现实世界中周期现象的一种数学模型,可以用来研究很多问题,在刻画周期变化规律、预测未来等方面发挥重要作用.
解三角函数应用问题的基本步骤
函数y=Asin(ωx+φ),A>0,ω>0中参数的物理意义
三角函数在物理中的应用
处理物理学问题的策略
(1)常涉及的物理学问题有单摆、光波、电流、机械波等,其共同的特点是具有周期性.
(2)明确物理概念的意义,此类问题往往涉及诸如频率、振幅等概念,因此要熟知其意义并与对应的三角函数知识结合解题.
例题研究
一、三角函数在生活中的应用
题型探究
例题1
为了研究钟表与三角函数的关系,建立如图所示的平面直角坐标系,设秒针针尖指向位置.若初始位置为,秒针从(注:此时)开始沿顺时针方向走动,则点的纵坐标与时间的函数关系式为( )
A. B.
C. D.
【答案】C
【分析】根据条件先确定周期从而求解出的值,设出与时间的函数关系式(注意秒针是顺时针方向转动),根据初始位置计算出的值从而求解出关系式.
【详解】
由题意,函数的周期为,∴.
设函数解析式为(秒针是顺时针走动).
∵初始位置为,∴时,.∴,可取.
∴函数的解析式为.
故选C.
【点睛】考查利用三角函数的实际模型求解函数解析式
例题2
九章算术是我国古代著名数学经典其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小以锯锯之,深一寸,锯道长一尺问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示阴影部分为镶嵌在墙体内的部分已知弦尺,弓形高寸,估算该木材镶嵌在墙中的体积约为(注:1丈尺寸,,)
A.600立方寸 B.610立方寸 C.620立方寸 D.633立方寸
【答案】D
【分析】由三角形,利用勾股定理可得半径,进而得,再利用,乘以高即可得体积.
【详解】
连接,设⊙的半径为,
则,所以.
由于,
所以,即.
所以 平方寸.
∴该木材镶嵌在墙中的体积为立方寸,
故选D.
【点睛】考查了垂径定理和勾股定理及扇形的面积公式,柱体的体积公式,属于中档题
跟踪训练
训练1
某同学在做研究性学习时发现,在邢台大峡谷景区,每年到访的游客人数会发生周期性的变化.现假设该风景区每年各个月份游客的人数(单位:万人)可近似地用函数来刻画.其中:正整数表示月份且,例如时表示二月份;和是正整数;.统计发现,风景区每年各个月份游客人数有以下规律:
①每一年相同的月份,该风景区游客人数大致相同;
②该景区游客人数最多的八月份和最少的二月份相差约400000人;
③二月份该风景区游客大约为100000人,随后逐渐增加,八月份达到最多.
(1)试根据已知信息,确定一个符合条件的的表达式;
(2)一般地,当该地区游客超过400000人时,该风景区也进入了一年中的旅游“旺季”.那么,一年中的哪几个月是该风景区的旅游“旺季”?请说明理由.
【答案】(1);(2)一年中的7,8,9,10四个月是该风景区的旅游“旺季”,理由见解析.
【分析】
(1)由实际问题的周期性且周期为、淡旺季数据,结合数学模型即可求,,进而可得表达式;
(2)由(1)结合已知条件即可求出的范围,结合实际条件即可知旺季所含月份.
【详解】
(1)根据三条规律,可知该函数为周期函数且周期为12,可得,即,
由规律②③可知,,解得:,
综上可得,;
(2)由条件,,可得
∴,,即,
又,,所以,,故:,8,9,10,
即一年中的7,8,9,10四个月是该风景区的旅游“旺季”.
【点睛】考查了三角函数的实际应用.
训练2
平潭国际“花式风筝冲浪”集训队,在平潭龙凤头海滨浴场进行集训,海滨区域的某个观测点观测到该处水深(米)是随着一天的时间(,单位小时)呈周期性变化,某天各时刻的水深数据的近似值如下表:
(1)根据表中近似数据画出散点图(坐标系在答题卷中),观察散点图,选择一个合适的函数模型,并求 出该拟合模型的函数解析式;
(2)为保证队员安全,规定在一天中的时且水深不低于1.05米的时候进行训练,根据(1)中的选择的函数解析式,试问:这一天可以安排什么时间段组织训练,才能确保集训队员的安全.
【答案】(1)(2)这一天可以安排早上5点至7点以及11点至18点的时间段组织训练, 才能确保集训队员的安全.
【解析】
分析:(1)根据表中近似数据画出散点图,选做为函数模型,由此利用三角函数的图象和性质能求出该拟合模型的函数解析式.
(2)由(1)知:,令,即,从而,由此能求出这一天可以安排早上5点至7点以及11点至18点的时间段组织训练,才能确保集训队员的安全.
详解:
(1)根据表中近似数据画出散点图,如图所示:
依题意,选做为函数模型,
∴
∵ ∴
∴
又∵函数的图象过点
∴,∴
∴.
(2)由(1)知:
令,即
∴
∴
∴
又∵
∵或
∴这一天可以安排早上5点至7点以及11点至18点的时间段组织训练, 才能确保集训队员的安全.
二、几何中的三角函数模型
题型探究
例题1
如图,“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设大正方形的面积为,小正方形的面积为,且,则( )
A. B.
C.2 D.3
【答案】B
【分析】设大正方形的边长为,则由已知条件可得小正方形的边长为,设为,在在中,由勾股定理得, ,可求得,所以
【详解】
解:设大正方形的边长为,
因为,所以,得,
所以小正方形的边长为,
所以,
设为,则,
在中,由勾股定理得,
所以,
解得或(舍去),
所以
故选:B
例题2
2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图所示).已知大正方形边长为10,小正方形边长为2.设较小直角边a所对的角为,则的值为( )
A. B. C. D.
【答案】B
【分析】由题意可知,利用勾股定理可求出,从而可求出的值.
【详解】
由题意可得,所以,
解得或(舍去),故,
所以,
故选:B
【点睛】考查了勾股定理的应用
跟踪训练
训练1
如图,在扇形中,半径,圆心角,是扇形弧上的动点,矩形内接于扇形,记,矩形的面积为.
(1)用含的式子表示线段,的长;
(2)求的最大值.
【答案】(1),;,;(2).
【分析】
(1)在和中利用三角函数的定义可表示出;
(2)求出后可得矩形面积,利用二倍角公式,两角和的正弦公式化函数为一个角的一个三角函数形式,然后由正弦函数性质可得最大值.
【详解】
解:(1)在中,,∴,,
又中,,,
∴,;
(2)在中,,∴,
∴
,
∵,∴,
∴当即时,.
【点睛】考查三角函数的应用,解题关键是用角表示出矩形面积,然后可利用三角函数的恒等变换公式如二倍角公式、两角和与差的正弦(余弦)公式、诱导公式等化函数为一个角的一个三角函数形式,即形式,最后利用正弦函数性质求得结论.
训练2
如图,已知中,.设,,它的内接正方形的一边在斜边上,、分别在、上.假设的面积为,正方形的面积为.
(Ⅰ)用表示的面积和正方形的面积;
(Ⅱ)设,试求的最大值,并判断此时的形状.
【答案】(Ⅰ),;,(Ⅱ)最大值为;为等腰直角三角形
【分析】
(Ⅰ)根据直角三角形,底面积乘高是面积;然后考虑正方形的边长,求出边长之后,即可表示正方形面积;
(Ⅱ)化简的表达式,利用基本不等式求最值,注意取等号的条件.
【详解】
解:(Ⅰ)∵在中,∴,. ∴
∴,
设正方形边长为,则,,
∴.
∴,
∴,
(Ⅱ)解:由(Ⅰ)可得
,
令,
∵在区间上是减函数
∴当时,取得最小值, 即取得最大值.
∴的最大值为
此时
∴为等腰直角三角形
【点睛】(1)函数的实际问题中,不仅要根据条件列出函数解析式时,同时还要注意定义域;
(2)求解函数的最值的时候,当取到最值时,一定要添加增加取等号的条件.
综合式测试
一、单选题
1.某地市委、市政府坚持创新、协调、绿色、开放、共享的发展理念,把高质量发展同满足人民美好生活需要紧密结合起来,坚持生态优先.下图是该市某公园三期规划的一角示意图.边长为3百米的正方形花圃的中,建有是以为圆心,1百米为半径的扇形水池,现需在其余部分设计一个矩形草坪,其中是水池边上任意一点,点,分别在边和上,则规划中矩形草坪面积的最小值为( )平方百米.
A. B. C.4 D.6
【答案】B
【分析】设∠PAB=θ,过P作PE垂直AB于点E,进而用表示出了矩形PNCQ的边长,即可解出.
【详解】
,设,过P作PE垂直AB于点E,如图:
,
时,面积有最小值,
故选:B
2.如图,一个摩天轮的半径为10m,轮子的最低处距离地面2m.如果此摩天轮按逆时针匀速转动,每30分钟转一圈,且当摩天轮上某人经过点(点与摩天轮天轮中心的高度相同)时开始计时,在摩天轮转动的一圈内,此人相对于地面的高度不小于17m的时间大约是( )
A.8分钟 B.10分钟 C.12分钟 D.14分钟
【答案】B
【分析】由题可得此人相对于地面的高度与时间的关系是,再令求出的范围即可得出.
【详解】
设时间为时,此人相对于地面的高度为,
则由题可得当时,,
在时间时,此人转过的角为,
此时此人相对于地面的高度,
令,则,
所以,解得,
故在摩天轮转动的一圈内,此人相对于地面的高度不小于17m的时间大约是.
故选:B.
【点睛】考查三角函数的实际应用,解题的关键是得出高度与时间的关系,再解三角函数不等式即可.
3.函数,若,则的最小值是( )
A. B. C. D.
【答案】A
【分析】化简得,由可知在,处取到最大值和最小值,不妨设在处有最大值,处取到最小值,可得,,,即可求出的最小值.
【详解】
,
∴函数的最大值为3,最小值为﹣1,
又,∴在,处取到最大值和最小值,
不妨设在处有最大值,则,即,
处取到最小值,则,即,
所以,,,
所以当时,的最小值为.
【点睛】
结论点睛:正弦型函数最值:
① ,当, 时取最大值;
②,当, 时取最小值.
4.一观览车的主架示意图如图所示,其中为轮轴的中心,距地面(即长),巨轮的半径长为,,巨轮逆时针旋转且每分钟转一圈,若点为吊舱的初始位置,经过分钟,该吊舱距离地面的高度为( )
A. B.
C. D.
【答案】B
【分析】
先通过计算得出转动的角速度,然后利用三角函数模型表示在转动的过程中点的纵坐标满足的关系式,则吊舱到底面的距离为点的纵坐标减.
【详解】
如图所示,以点为坐标原点,以水平方向为轴,以所在直线为轴建立平面直角坐标系.
因为巨轮逆时针旋转且每分钟转一圈,则转动的角速度为每分钟,
经过分钟之后,转过的角度为,
所以,在转动的过程中,点的纵坐标满足:
则吊舱距离地面的距离.
故选:B.
【点睛】
建立三角函数模型解决实际问题的一般步骤:
(1)审题:审清楚题目条件、要求、理解数学关系;
(2)建模:分析题目变化趋势,选择合适的三角函数模型;
(3)求解:对所建立的数学模型进行分析研究,从而得到结论.
5.为迎接大运会的到来,学校决定在半径为,圆心角为的扇形空地的内部修建一平行四边形观赛场地,如图所示.则观赛场地的面积最大值为( )
A. B.
C. D.
【答案】D
【分析】
如图,连接,设,可用的三角函数值表示,,即可得到四边形的面积,再根据三角函数的值域的求法即可求解.
【详解】
如图所示: .
连接,设,作,,垂足分别为.
根据平面几何知识可知,,,.
∴,.
故四边形的面积也为四边形的面积,
即有
,其中.
所以当即时,.
故选:D.
【点睛】考查利用三角函数解决几何中的最值问题,意在考查学生的数学建模能力和数学运算能力,属于基础题.
6.如图所示,秒针尖的位置为,若初始位置为,当秒针从(此时)正常开始走时,那么点M的横坐标与时间t的函数关系为( )
A. B.
C. D.
【答案】C
【分析】
根据条件先确定周期从而求解出的值,设出与时间的函数关系式(注意秒针是顺时针方向转动),根据初始位置,计算出的值从而求解出关系式.
【详解】
初始角为,周期,所以,,
设与时间的函数关系式(因为秒针是顺时针走动)
所以,当秒针运动到M点时,.
故选:C.
【点睛】考查利用三角函数的实际模型求解函数解析式,难度一般.钟表问题的三角函数实际模型中,由于分针、时针、秒针都是顺时针转动,因此在确定的时候要注意取负值,这里依据的是角的正负的定义.
7.动点在圆上绕坐标原点沿逆时针方向匀速旋转,其初始位置为,12秒旋转一周,则动点的纵坐标关于时间(单位:秒)的函数式为( )
A. B.
C. D.
【答案】C
【分析】设关于的函数:,根据周期求出,再根据过点求出,问题得以解决.
【详解】
设关于的函数:
动点12秒旋转一周,则 ,得.
动点的初始位置为.
即时,,即,则可取
所以
故选:C
【点睛】考查函数的解析式的求法,体现了转化的数学思想,属于中档题.
8.车流量被定义为单位时间内通过十字路口的车辆数,单位为辆/分钟.若上班高峰期某十字路口的车流量(单位:辆/分钟)与时间(单位:分钟)的函数关系式为,则下列哪个时间段内车流量是增加的( )
A. B. C. D.
【答案】C
【分析】
由题意可知,问题是求函数在上的单调递增区间的子集,即先求出该函数在上的增区间,与取交集,并判断每个选项中的区间与单调增区间的包含关系即可得出合适选项.
【详解】
令,.
,当时,函数的单调递增区间为,当时,函数的单调递增区间为.
,车流量在时间段内是增加的,
故选:C.
【点睛】考查三角函数的实际应用,将问题转化为三角函数的单调性是解答的关键,考查分析问题和解决问题的能力,属于中等题.
二、填空题
9.哈尔滨文化公园的摩天轮始建于2003年1月15日,2003年4月30日竣工,是当时中国第一高的巨型摩天轮,其旋转半径50米,最高点距地地面110米,运行一周大约21分钟.某人在最低点的位置坐上摩天轮,则第14分钟时他距地面大约为__米.
【答案】85
【分析】
设与地面高度与时间的关系,,,,,根据已知求出,即得解.
【详解】
设与地面高度与时间的关系,,,,,
由题意可知:,,,,
即,
又因为,即,故,,
所以第14分钟时他距地面大约为.
故答案为:85.
【点睛】方法点睛:求三角函数的解析式,通常用待定系数法,先定式(设出三角函数的解析式),再定量(解方程组求出待定系数).
10.如图,以正方形的各边为底可向外作四个腰长为1的等腰三角形,则阴影部分面积的最大值是___________.
【答案】
【分析】
设等腰三角形底角为,阴影面积为,根据正弦函数的图象与性质即可得到结果.
【详解】
设等腰三角形底角为,则等腰三角形底边长为高为,
阴影面积为:
,
当时,阴影面积的最大值为
故答案为
【点睛】考查平面图形的面积问题,考查三角函数的图象与性质,解题关键用等腰三角形底角为表示等腰三角形的底边与高.
11.如图,游乐场所的摩天轮匀速旋转,每转一周需要l2min,其中心O离地面45米,半径40米.如果你从最低处登上摩天轮,那么你与地面的距离将随时间的变化而变化,以你登上摩天轮的时刻开始计时,请问:当你第六次距离地面65米时,用了________分钟?
【答案】32.
【分析】
根据题意得到,化简得到或,得到答案.
【详解】
设时间为,,根据题意:,故.
故或,故或,.
故.
故答案为:.
【点睛】考查了三角函数的应用,意在考查学生的应用能力.
12.如图,货轮在海上以的速度沿着方位角(从指北方向顺时针转到目标方向线的水平角)为150°的方向航行.为了确定船位,在点B观察灯塔A的方位角是120°,航行半小时后到达C点,观察灯塔A的方位角是75°,则货轮到达C点时与灯塔A的距离为______ n mile
【答案】
【分析】
通过方位角定义,求出,,利用正弦定理即可得到答案.
【详解】
根据题意,可知,,,因此可得,由正弦定理得:,求得,即答案为.
【点睛】考查正弦定理的实际应用,难度不大.
三、解答题
13.现有一块半径为,圆心角为的扇形铁皮废料,现在准备利用这块铁皮制作一些图形模型.已知点P在弧上,设.
图1 图2
(1)方案1:过点P裁剪一个扇形内接矩形(如图1),点Q在上,点M,N在上,
①若,求矩形的面积;
②若矩形是正方形,求的值;
(2)方案2:从P点处分别向作两条垂线和,垂足为S,T,(如图2)这样可以裁剪出两个直角三角形和,为了提高废料的利用率,我们希望这两个直角三角形面积和最大,试问此时点P应在何处?请说明你的理由.
【答案】(1)①,②;(2)点为的中点.
【分析】
(1)①由题意可用表示出,即可求出矩形的面积;
②在中,直接表示出角的正切,即可得到结果;
(2)将两个三角形的面积和表示出来,然后利用三角函数知识即可求解.
【详解】
(1)①因为,所以,因为,所以,则,所以,故;
②设,在中,,所以,在中,;
(2)因为,所以,
所以
,
当,即 ,所以时,即点为的中点时,这两个直角三角形面积和最大,
14.圣·索菲亚教堂(SAINT SOPHIA CATHEDRAL)是一座始建于1907年拜占庭风格的东正教教堂,为哈尔滨的标志性建筑,1996年经国务院批准,被列为第四批全国重点文物保护单位,是每一位到哈尔滨旅游的游客拍照打卡的必到景点,其中央主体建筑集球、圆柱、棱柱于一体,极具对称之美,可以让游客从任何角度都能领略它的美,如左图.某校高一数学兴趣小组打算根据所学知识估算索菲亚教堂的高度,他们在索菲亚教堂的正东方向找到一座建筑物,测得建筑物的高度为h,在它们之间的地面上的点M(B,M,D三点共线)处可以测得楼顶A和教堂顶C的仰角分别为和,在楼顶A处可测得塔顶C的仰角为,且与都垂直地面,如右图,那么请你根据他们测得的数据估算索菲亚教堂的高度为多少?(结果用h,,,表示)
【答案】高度为.
【分析】
设,首先根据题目示意图,分析得到,,,,最后在中利用正弦定理得到求解.
【详解】
解:由题可知,在中,,
设,
则,
在中,,
则.
在中,
∴
由正弦定理可知
,
即.
∴
答:索菲亚教堂的高度为.
【点睛】解三角形应用题的一般步骤:
(1)阅读理解题意,弄清问题的实际背景,明确已知与未知,理清量与量之间的关系.
(2)根据题意画出示意图,将实际问题抽象成解三角形问题的模型.
(3)根据题意选择正弦定理或余弦定理求解.
(4)将三角形问题还原为实际问题,注意实际问题中的有关单位问题、近似计算的要求等.
15.如图,直角坐标系建立在湖泊的某一恰当位置,现准备在湖泊的一侧修建一条观光大道,它的前一段是以为圆心,为半径的圆弧,后一段是函数,时的图像,图像的最高点为.
(1)求函数的解析式;
(2)若在湖泊内修建如图的矩形水上乐园,其中折线为水上赛艇线路,问点落在圆弧上何处时赛艇线路最长?
【答案】(1),;(2)当点坐标为时赛艇线路最长.
【分析】
(1)由图可知,,即可求出,将代入可求;
(2)求出的坐标,连接,设,将赛艇线路长表示为关于的三角函数形式,即可根据三角函数性质求解.
【详解】
(1)由图象知,,即,则,
将代入,则,
则,又,,
所以,;
(2)在中令,得,∴.
连接,设,,则.
设赛艇线路长为,则,
当时,有最大值,此时.
所以当点坐标为时赛艇线路最长.
10 / 37
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
