【精选备课】2022-2023学年数学湘教版(2012)九年级上册 第四单元测试(含解析 )
文档属性
| 名称 | 【精选备课】2022-2023学年数学湘教版(2012)九年级上册 第四单元测试(含解析 ) |

|
|
| 格式 | doc | ||
| 文件大小 | 607.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-22 00:00:00 | ||
图片预览



文档简介
第四单元测试
一、单选题
1.如图,在的正方形网格中,每个小正方形的边长都是1,的顶点都在这些小正方形的顶点上,那么的值为( ).
A. B. C. D.
2.如图,有一斜坡的长米,坡角,则斜坡的铅垂高度为( ).
A. B. C. D.
3.如图,在矩形ABCD中,点E在DC上,将矩形沿AE折叠,使点D落在BC边上的点F处.若AB=3,BC=5,则tan∠DAE的值为( )
A. B. C. D.
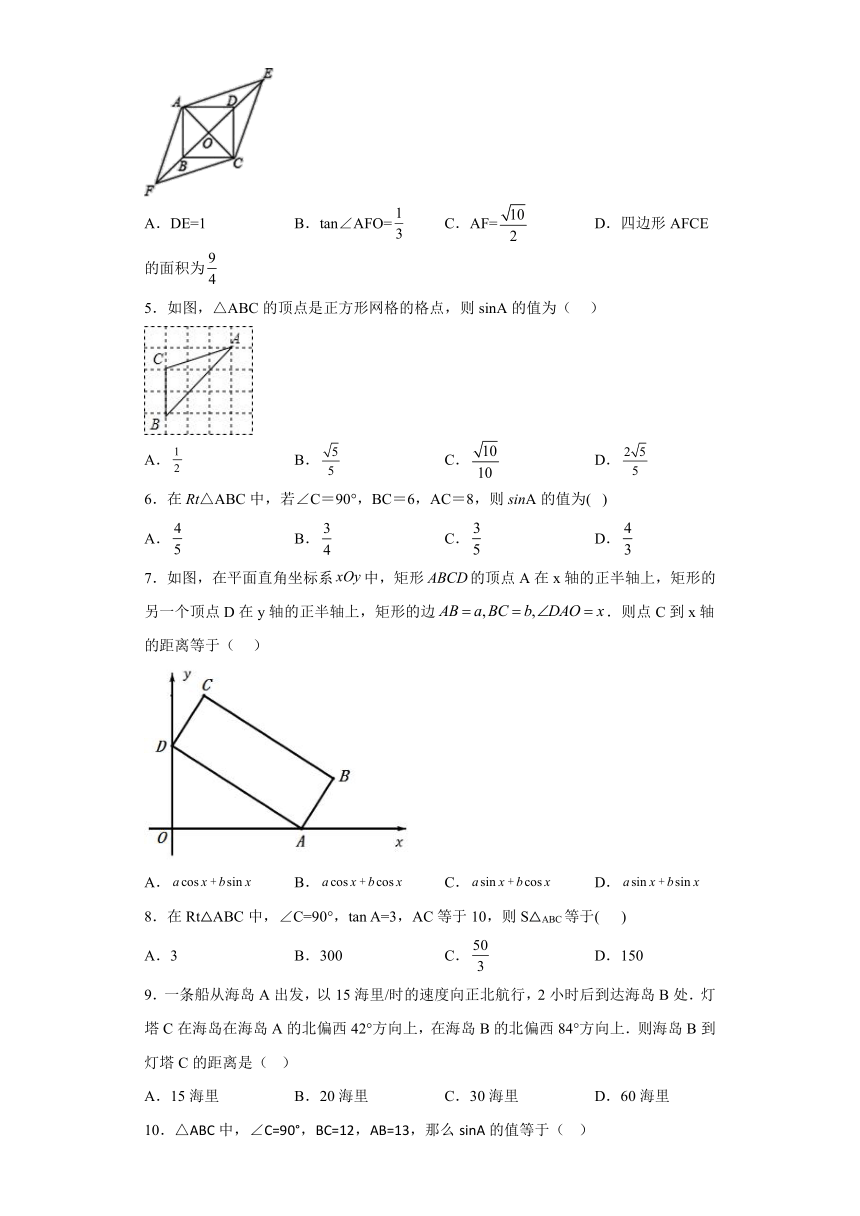
4.如图,四边形ABCD是边长为1的正方形,E,F为BD所在直线上的两点,若AE=,∠EAF=135°,则下列结论正确的是( )
A.DE=1 B.tan∠AFO= C.AF= D.四边形AFCE的面积为
5.如图,△ABC的顶点是正方形网格的格点,则sinA的值为( )
A. B. C. D.
6.在Rt△ABC中,若∠C=90°,BC=6,AC=8,则sinA的值为( )
A. B. C. D.
7.如图,在平面直角坐标系中,矩形的顶点A在x轴的正半轴上,矩形的另一个顶点D在y轴的正半轴上,矩形的边.则点C到x轴的距离等于( )
A. B. C. D.
8.在Rt△ABC中,∠C=90°,tan A=3,AC等于10,则S△ABC等于( )
A.3 B.300 C. D.150
9.一条船从海岛A出发,以15海里/时的速度向正北航行,2小时后到达海岛B处.灯塔C在海岛在海岛A的北偏西42°方向上,在海岛B的北偏西84°方向上.则海岛B到灯塔C的距离是( )
A.15海里 B.20海里 C.30海里 D.60海里
10.△ABC中,∠C=90°,BC=12,AB=13,那么sinA的值等于( )
A. B. C. D.
二、填空题
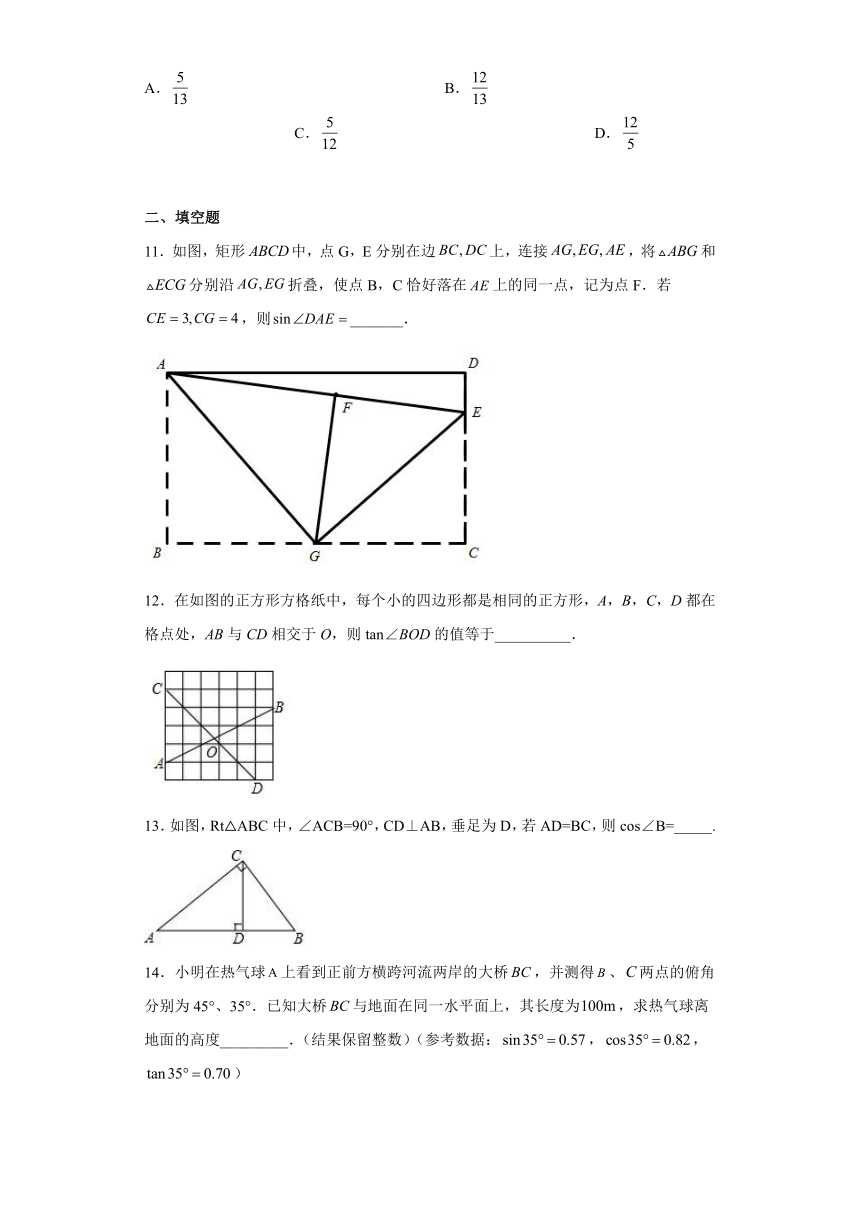
11.如图,矩形中,点G,E分别在边上,连接,将和分别沿折叠,使点B,C恰好落在上的同一点,记为点F.若,则_______.
12.在如图的正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D都在格点处,AB与CD相交于O,则tan∠BOD的值等于__________.
13.如图,Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AD=BC,则cos∠B=_____.
14.小明在热气球上看到正前方横跨河流两岸的大桥,并测得、两点的俯角分别为45°、35°.已知大桥与地面在同一水平面上,其长度为,求热气球离地面的高度_________.(结果保留整数)(参考数据:,,)
15.如图,在△ABC中,∠A=90°,∠B=60°,AB=2,若D是BC边上的动点,则2AD+DC的最小值为_____.
三、解答题
16.如图,在△ABC中,∠ACB=90°,∠CAB=30°, △ABD是等边三角形,将四边形ACBD沿直线EF折叠,使D与C重合,CE与CF分别交AB于点G、H.
(1)求证:△AEG∽△CHG;
(2)△AEG与△BHF是否相似,并说明理由;
(3)若BC=1,求cos∠CHG的值.
17.热气球的探测器显示,从热气球A处看大楼BC顶部C的仰角为30°,看大楼底部B的俯角为45°,热气球与该楼的水平距离AD为60米,求大楼BC的高度.(结果精确到1米,参考数据:)
18.如图,在中,是对角线、的交点,,,垂足分别为点、.
(1)求证:.
(2)若,,求的值.
19.如图,两楼地面距离BC为米,楼AB高30米,从楼AB的顶部点A测得楼CD顶部点D的仰角为45度.
(1)求的大小;
(2)求楼CD的高度(结果保留根号).
20.在南部沿海某气象站A测得一热带风暴从A的南偏东30°的方向迎着气象站袭来,已知该风暴速度为每小时20千米,风暴周围50千米范围内将受到影响,若该风暴不改变速度与方向,问气象站正南方60千米处的沿海城市B是否会受这次风暴的影响?若不受影响,请说明理由;若受影响,请求出受影响的时间.
参考答案:
1.D
【分析】过点A作于点D,在中,利用勾股定理求得线段AC的长,再按照正弦函数的定义计算即可.
【详解】解:如图,过点A作于点D,则,
∴,
∴,
故选:D.
【点睛】本题考查了勾股定理的运用以及锐角三角函数,正确作出辅助线是解题的关键.
2.C
【分析】根据三角函数的定义,结合题意,即可得到答案.
【详解】结合题意,得:
∴
故选:C.
【点睛】本题考查了三角函数的知识;解题的关键是熟练掌握三角函数的定义,从而完成求解.
3.D
【分析】先根据矩形的性质和折叠的性质得AF=AD=BC=5,EF=DE,在Rt△ABF中,利用勾股定理可求出BF的长,则CF可得,设CE=x,则DE=EF=3﹣x,然后在Rt△ECF中根据勾股定理可得关于x的方程,解方程即可得到x,进一步可得DE的长,再根据正切的定义即可求解.
【详解】解:∵四边形ABCD为矩形,
∴AD=BC=5,AB=CD=3,
∵矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的F处,
∴AF=AD=5,EF=DE,
在Rt△ABF中,BF=,
∴CF=BC﹣BF=5﹣4=1,
设CE=x,则DE=EF=3﹣x
在Rt△ECF中,∵CE2+FC2=EF2,
∴x2+12=(3﹣x)2,解得x=,
∴DE=EF=3﹣x=,
∴tan∠DAE=,
故选:D.
【点睛】本题考查了翻折变换、矩形的性质、锐角三角函数和勾股定理等知识,属于常考题型,灵活运用这些性质进行推理与计算是解题的关键.
4.C
【分析】根据正方形的性质求出AO的长,用勾股定理求出EO的长,然后由∠EAF=135°及∠BAD=90°可以得到相似三角形,根据相似三角形的性质求出BF的长,再一一计算即可判断.
【详解】∵四边形ABCD是正方形,
∴AB=CB=CD=AD=1,AC⊥BD,∠ADO=∠ABO=45°,
∴OD=OB=OA=,∠ABF=∠ADE=135°,
在Rt△AEO中,EO=,
∴DE=,故A错误.
∵∠EAF=135°,∠BAD=90°,
∴∠BAF+∠DAE=45°,
∵∠ADO=∠DAE+∠AED=45°,
∴∠BAF=∠AED,
∴△ABF∽△EDA,
∴,
∴,
AF=,故C正确,
OF=
tan∠AFO=,故B错误,
∴S四边形AECF= AC EF=××=,故D错误,
故选C.
【点睛】本题考查的是相似三角形的判定与性质,根据正方形的性质,运用勾股定理求出相应线段的长,再根据∠EAF=135°和∠BAD=90°,得到相似三角形,用相似三角形的性质求出AF的长,然后根据对称性求出四边形的面积.
5.B
【分析】先利用勾股定理得出DC,AC、AD的长,根据勾股定理的逆定理可得∠CDA=90°,再利用锐角三角函数关系求出答案.
【详解】解:如图所示,取格点D,连接DC,
由网格可得出DC=,AC=,AD=,
∵,
∴,
则:∠CDA=90°,
故sinA=.
故选:B.
【点睛】本题考查了网格中解直角三角形、勾股定理及其逆定理、锐角的三角函数,根据网格特点构造直角三角形是关键.
6.C
【详解】试题解析:
故选C.
7.A
【分析】作CE⊥y轴于E.解直角三角形求出OD,DE即可解决问题.
【详解】作CE⊥y轴于E.
在Rt△OAD中,
∵∠AOD=90°,AD=BC=,∠OAD=,
∴OD=,
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴∠CDE+∠ADO=90°,
又∵∠OAD+∠ADO=90°,
∴∠CDE=∠OAD=,
∴在Rt△CDE中,
∵CD=AB=,∠CDE=,
∴DE=,
∴点C到轴的距离=EO=DE+OD=,
故选:A.
【点睛】本题考查了解直角三角形的应用,矩形的性质,正确作出辅助线是解题的关键.
8.D
【分析】根据tanA==3即可求得BC的长,进而求出面积.
【详解】∵tanA= =3,
∴BC=AC tanA=10×3=30,
∴S△ABC=AC BC=×10×30=150.
故选D.
【点睛】本题考查了解直角三角形.掌握正切的概念是解题的关键.
9.C
【分析】根据题意画出图形,根据三角形外角性质求出∠C=∠CAB=42°,根据等角对等边得出BC=AB,求出AB即可.
【详解】解:∵根据题意得:∠CBD=84°,∠CAB=42°,
∴∠C=∠CBD-∠CAB=42°=∠CAB,
∴BC=AB,
∵AB=15海里/时×2时=30海里,
∴BC=30海里,
即海岛B到灯塔C的距离是30海里.
故选C.
【点睛】本题考查了等腰三角形的性质和判定和三角形的外角性质,关键是求出∠C=∠CAB,题目比较典型,难度不大.
10.B
【分析】根据正弦的定义:正弦=对边/斜边即可解答.
【详解】由题意得sinA==,故选B.
【点睛】掌握正弦公式是解答本题的关键.
11.
【分析】根据折叠的性质结合勾股定理求得GE,BC=AD=8,证得Rt△EGFRt△EAG,求得,再利用勾股定理得到DE的长,即可求解.
【详解】矩形中,GC=4,CE =3,∠C=90,
∴GE=,
根据折叠的性质:BG=GF,GF=GC=4,CE=EF=3,∠AGB=∠AGF,∠EGC=∠EGF,∠GFE =∠C=90,
∴BG=GF=GC=4,
∴BC=AD=8,
∵∠AGB+∠AGF+∠EGC+∠EGF=180,
∴∠AGE=90,
∴Rt△EGFRt△EAG,
∴,即,
∴,
∴DE=,
∴,
故答案为:.
【点睛】本考查了折叠的性质,矩形的性质,勾股定理的应用,相似三角形的判定和性质,锐角三角形函数的知识等,利用勾股定理和相似三角形的性质求线段的长度是本题的关键.
12.3
【详解】试题解析:平移CD到C′D′交AB于O′,如图所示,
则∠BO′D′=∠BOD,
∴tan∠BOD=tan∠BO′D′,
设每个小正方形的边长为a,
则O′B=,O′D′=,BD′=3a,
作BE⊥O′D′于点E,
则BE=,
∴O′E=,
∴tanBO′E=,
∴tan∠BOD=3.
考点:解直角三角形.
13.
【分析】设AD=BC=x,可证△ABC∽△CBD,根据相似三角形的性质表示出BD的长,然后在△Rt△BCD中,利用余弦的定义求解即可.
【详解】设AD=BC=x,
∵∠ACB=90°,CD⊥AB,
∴∠A+∠ACD=∠ACD+∠BCD=90°,
∴∠A=∠BCD,
∴△ABC∽△CBD,
∴,即,
∴BD=x,
∴cos∠B==,
故答案为.
【点睛】本题考查了相似三角形的判定与性质,锐角三角函数的定义,由△ABC∽△CBD表示出BD的长是解答本题的关键.
14.233m
【分析】作AD⊥BC交CB的延长线于D,设AD为x,表示出DB和DC,根据正切的概念求出x的值即可.
【详解】解:作AD⊥BC交CB的延长线于D,设AD为x,
由题意得,∠ABD=45°,∠ACD=35°,
在Rt△ADB中,∠ABD=45°,
∴DB=x,
在Rt△ADC中,∠ACD=35°,
,
,
解得,x≈233.
所以,热气球离地面的高度约为233米.
故答案为:233.
【点睛】本题考查的是解直角三角形的应用,理解仰角和俯角的概念、掌握锐角三角函数的概念是解题的关键,解答时,注意正确作出辅助线构造直角三角形.
15.6
【分析】取AC的中点F,过F作于G,延长FG至E,使EG=FG,连接AE交BC于D,则 此时最短,证明此时D为BC的中点,证明CD=2DF,从而可得答案.
【详解】解:如图,
取AC的中点F,过F作于G,延长FG至E,使EG=FG,连接AE交BC于D,则 此时最短,
过A作于H,则由
为BC的中点,
即的最小值为6.
故答案为:6.
【点睛】本题考查的是利用轴对称求最小值问题,考查了锐角三角函数,三角形的相似的判定与性质,直角三角形的性质,勾股定理的应用,掌握以上知识是解题的关键.
16.(1)证明见解析(2)△AEG与△BHF相似 (3)
【详解】试题分析:(1)由于△ABD是等边三角形,那么∠D=∠EAG=60°,根据折叠的性质知:∠D=∠GCH=∠AEG=60°,再加上对顶角∠EGA=∠HGC,即可证得所求的三角形相似;
(2)由△ABD是等边三角形和的性质知:∠BAD=∠GCH=∠ABD,再由三角形内角和定理可证明∠1=∠5,即可得到结论;
(3)在Rt△ABC中,已知了BC的长和∠BAC的度数,即可求得AB、AC的值,由折叠的性质知:DE=CE,可设出DE、CE的长,然后表示出AE的长,进而可在Rt△AEC中,由勾股定理求得AE、CE的值,即可得到∠AEG的余弦值,而根据(1)的相似三角形知∠AEG=∠CHG,由此得解.
试题解析:解:(1)∵△ABD是等边三角形,∴∠EAG=∠D=60°;
根据折叠的性质知:DE=CE,∠D=∠GCH=∠EAG=60°,又∵∠EGA=∠HGC,∴△AEG∽△CHG.
(2)△AEG与△BHF相似.理由如下:
∵∠BAD=∠ABD=∠D,∠GCH=∠D,∴∠BAD=∠GCH=∠ABD,∴∠1+∠2=∠3+∠4.∵∠2=∠3,∠4=∠5,∴∠1=∠5, ∴△AEG∽△BHF;
(3)△ABC中,∠BAC=30°,BC=1,则AC=,AB=2,故AD=AB=2.
设DE=EC=x,则AE=2﹣x.
在Rt△AEC中,由勾股定理,得:(2﹣x)2+3=x2,解得x=,∴AE=,EC=,∴cos∠AEC==.由(1)的相似三角形知:∠AEG=∠CHG,故cos∠CHG=cos∠AEC=.
点睛:此题考查的知识点有:等边三角形的性质、相似三角形的判定和性质、图形的翻折变换以及锐角三角函数的定义等知识,难度适中.
17.这栋楼的高度约为95米.
【分析】利用正切函数分别在Rt△ABD与Rt△ACD中求得BD与CD的长即可.
【详解】由题意可知,,米,
在中,(米),
在中,(米),
(米).
答:这栋楼的高度约为95米.
【点睛】本题考查了解直角三角形的应用,准确确定直角三角形,灵活运用相关知识是解此题的关键.
18.(1)见解析1;(2)
【分析】(1)根据题意由平行四边形性质得,由ASA证得,即可得出结论;
(2)根据题意由(1)得OE=OF,则OE=2,在Rt△OEB中,由三角函数定义即可得出结果.
【详解】解:(1)证明:在中,
∵,
∴
∴
又∵
∴
∴
(2)∵,
∴
∵
∴
在中,,.
【点睛】本题考查平行四边形的性质、全等三角形的判定与性质、三角函数定义等知识;熟练掌握平行四边形的性质与全等三角形的判定是解题的关键.
19.(1)75°;(2)
【分析】(1)如图:过点A作于点E,在Rt△ABC中运用三角函数可得,即、进一步可得∠EAC=30°,再结合即可解答;
(2)先根据题意求得DE=AE=,然后在Rt△ACE中解直角三角形求得CE,最后利用CD=CE+DE进行计算即可.
【详解】(1)如图:过点A作于点E,
∵在Rt△ABC中,
∵AE//BC
;
(2)∵在RtAED中,AE=BC=,∠DAE=45°
∴DE=AE=
∵在Rt△ACE中,∠CAE=30°
∴CE=tan30°·AE=30
.
【点睛】本题主要考查了运用三角函数值求角的大小和解直角三角形,灵活应用三角函数知识是解答本题的关键.
20.沿海城市B会受到这次风暴的影响,受影响的时间为4小时
【分析】作出图像,求出风暴离B城市的最近距离BD= 30千米,判断出沿海城市B会受到这次风暴的影响,接下来计算受影响的时长,得沿海城市B受影响时风暴所走的路程为线段EF,求出EF的长,除以速度即可解题.
【详解】根据题意画出图形,
根据题意可知AB=60千米,∠BAF=30°
过B作BD⊥AF于点D,作BE=BF=50千米,分别交AF于点E、F
∵ BD⊥AF,AB=60千米,∠BAF=30°
∴ 风暴离B城市的最近距离为BD=AB×sin30°=30千米,
∵ BD<50千米
∴ 沿海城市B会受到这次风暴的影响
∵ BE=BF=50千米
∴ 沿海城市B受影响时风暴所走的路程为线段EF
∵ BE=BF=50千米,BD=30千米,BD⊥AF
∴ DF=DE=
∴ EF=2DF=80千米
∵ 风暴速度为每小时20千米
∴ 受影响时间==4小时
∴沿海城市B会受到这次风暴的影响,受影响的时间为4小时.
【点睛】本题主要考查了,含30°的特殊直角三角形的实际应用,中等难度,在理解题意的基础上求出BD与EF的长是解题关键.
一、单选题
1.如图,在的正方形网格中,每个小正方形的边长都是1,的顶点都在这些小正方形的顶点上,那么的值为( ).
A. B. C. D.
2.如图,有一斜坡的长米,坡角,则斜坡的铅垂高度为( ).
A. B. C. D.
3.如图,在矩形ABCD中,点E在DC上,将矩形沿AE折叠,使点D落在BC边上的点F处.若AB=3,BC=5,则tan∠DAE的值为( )
A. B. C. D.
4.如图,四边形ABCD是边长为1的正方形,E,F为BD所在直线上的两点,若AE=,∠EAF=135°,则下列结论正确的是( )
A.DE=1 B.tan∠AFO= C.AF= D.四边形AFCE的面积为
5.如图,△ABC的顶点是正方形网格的格点,则sinA的值为( )
A. B. C. D.
6.在Rt△ABC中,若∠C=90°,BC=6,AC=8,则sinA的值为( )
A. B. C. D.
7.如图,在平面直角坐标系中,矩形的顶点A在x轴的正半轴上,矩形的另一个顶点D在y轴的正半轴上,矩形的边.则点C到x轴的距离等于( )
A. B. C. D.
8.在Rt△ABC中,∠C=90°,tan A=3,AC等于10,则S△ABC等于( )
A.3 B.300 C. D.150
9.一条船从海岛A出发,以15海里/时的速度向正北航行,2小时后到达海岛B处.灯塔C在海岛在海岛A的北偏西42°方向上,在海岛B的北偏西84°方向上.则海岛B到灯塔C的距离是( )
A.15海里 B.20海里 C.30海里 D.60海里
10.△ABC中,∠C=90°,BC=12,AB=13,那么sinA的值等于( )
A. B. C. D.
二、填空题
11.如图,矩形中,点G,E分别在边上,连接,将和分别沿折叠,使点B,C恰好落在上的同一点,记为点F.若,则_______.
12.在如图的正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D都在格点处,AB与CD相交于O,则tan∠BOD的值等于__________.
13.如图,Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AD=BC,则cos∠B=_____.
14.小明在热气球上看到正前方横跨河流两岸的大桥,并测得、两点的俯角分别为45°、35°.已知大桥与地面在同一水平面上,其长度为,求热气球离地面的高度_________.(结果保留整数)(参考数据:,,)
15.如图,在△ABC中,∠A=90°,∠B=60°,AB=2,若D是BC边上的动点,则2AD+DC的最小值为_____.
三、解答题
16.如图,在△ABC中,∠ACB=90°,∠CAB=30°, △ABD是等边三角形,将四边形ACBD沿直线EF折叠,使D与C重合,CE与CF分别交AB于点G、H.
(1)求证:△AEG∽△CHG;
(2)△AEG与△BHF是否相似,并说明理由;
(3)若BC=1,求cos∠CHG的值.
17.热气球的探测器显示,从热气球A处看大楼BC顶部C的仰角为30°,看大楼底部B的俯角为45°,热气球与该楼的水平距离AD为60米,求大楼BC的高度.(结果精确到1米,参考数据:)
18.如图,在中,是对角线、的交点,,,垂足分别为点、.
(1)求证:.
(2)若,,求的值.
19.如图,两楼地面距离BC为米,楼AB高30米,从楼AB的顶部点A测得楼CD顶部点D的仰角为45度.
(1)求的大小;
(2)求楼CD的高度(结果保留根号).
20.在南部沿海某气象站A测得一热带风暴从A的南偏东30°的方向迎着气象站袭来,已知该风暴速度为每小时20千米,风暴周围50千米范围内将受到影响,若该风暴不改变速度与方向,问气象站正南方60千米处的沿海城市B是否会受这次风暴的影响?若不受影响,请说明理由;若受影响,请求出受影响的时间.
参考答案:
1.D
【分析】过点A作于点D,在中,利用勾股定理求得线段AC的长,再按照正弦函数的定义计算即可.
【详解】解:如图,过点A作于点D,则,
∴,
∴,
故选:D.
【点睛】本题考查了勾股定理的运用以及锐角三角函数,正确作出辅助线是解题的关键.
2.C
【分析】根据三角函数的定义,结合题意,即可得到答案.
【详解】结合题意,得:
∴
故选:C.
【点睛】本题考查了三角函数的知识;解题的关键是熟练掌握三角函数的定义,从而完成求解.
3.D
【分析】先根据矩形的性质和折叠的性质得AF=AD=BC=5,EF=DE,在Rt△ABF中,利用勾股定理可求出BF的长,则CF可得,设CE=x,则DE=EF=3﹣x,然后在Rt△ECF中根据勾股定理可得关于x的方程,解方程即可得到x,进一步可得DE的长,再根据正切的定义即可求解.
【详解】解:∵四边形ABCD为矩形,
∴AD=BC=5,AB=CD=3,
∵矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的F处,
∴AF=AD=5,EF=DE,
在Rt△ABF中,BF=,
∴CF=BC﹣BF=5﹣4=1,
设CE=x,则DE=EF=3﹣x
在Rt△ECF中,∵CE2+FC2=EF2,
∴x2+12=(3﹣x)2,解得x=,
∴DE=EF=3﹣x=,
∴tan∠DAE=,
故选:D.
【点睛】本题考查了翻折变换、矩形的性质、锐角三角函数和勾股定理等知识,属于常考题型,灵活运用这些性质进行推理与计算是解题的关键.
4.C
【分析】根据正方形的性质求出AO的长,用勾股定理求出EO的长,然后由∠EAF=135°及∠BAD=90°可以得到相似三角形,根据相似三角形的性质求出BF的长,再一一计算即可判断.
【详解】∵四边形ABCD是正方形,
∴AB=CB=CD=AD=1,AC⊥BD,∠ADO=∠ABO=45°,
∴OD=OB=OA=,∠ABF=∠ADE=135°,
在Rt△AEO中,EO=,
∴DE=,故A错误.
∵∠EAF=135°,∠BAD=90°,
∴∠BAF+∠DAE=45°,
∵∠ADO=∠DAE+∠AED=45°,
∴∠BAF=∠AED,
∴△ABF∽△EDA,
∴,
∴,
AF=,故C正确,
OF=
tan∠AFO=,故B错误,
∴S四边形AECF= AC EF=××=,故D错误,
故选C.
【点睛】本题考查的是相似三角形的判定与性质,根据正方形的性质,运用勾股定理求出相应线段的长,再根据∠EAF=135°和∠BAD=90°,得到相似三角形,用相似三角形的性质求出AF的长,然后根据对称性求出四边形的面积.
5.B
【分析】先利用勾股定理得出DC,AC、AD的长,根据勾股定理的逆定理可得∠CDA=90°,再利用锐角三角函数关系求出答案.
【详解】解:如图所示,取格点D,连接DC,
由网格可得出DC=,AC=,AD=,
∵,
∴,
则:∠CDA=90°,
故sinA=.
故选:B.
【点睛】本题考查了网格中解直角三角形、勾股定理及其逆定理、锐角的三角函数,根据网格特点构造直角三角形是关键.
6.C
【详解】试题解析:
故选C.
7.A
【分析】作CE⊥y轴于E.解直角三角形求出OD,DE即可解决问题.
【详解】作CE⊥y轴于E.
在Rt△OAD中,
∵∠AOD=90°,AD=BC=,∠OAD=,
∴OD=,
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴∠CDE+∠ADO=90°,
又∵∠OAD+∠ADO=90°,
∴∠CDE=∠OAD=,
∴在Rt△CDE中,
∵CD=AB=,∠CDE=,
∴DE=,
∴点C到轴的距离=EO=DE+OD=,
故选:A.
【点睛】本题考查了解直角三角形的应用,矩形的性质,正确作出辅助线是解题的关键.
8.D
【分析】根据tanA==3即可求得BC的长,进而求出面积.
【详解】∵tanA= =3,
∴BC=AC tanA=10×3=30,
∴S△ABC=AC BC=×10×30=150.
故选D.
【点睛】本题考查了解直角三角形.掌握正切的概念是解题的关键.
9.C
【分析】根据题意画出图形,根据三角形外角性质求出∠C=∠CAB=42°,根据等角对等边得出BC=AB,求出AB即可.
【详解】解:∵根据题意得:∠CBD=84°,∠CAB=42°,
∴∠C=∠CBD-∠CAB=42°=∠CAB,
∴BC=AB,
∵AB=15海里/时×2时=30海里,
∴BC=30海里,
即海岛B到灯塔C的距离是30海里.
故选C.
【点睛】本题考查了等腰三角形的性质和判定和三角形的外角性质,关键是求出∠C=∠CAB,题目比较典型,难度不大.
10.B
【分析】根据正弦的定义:正弦=对边/斜边即可解答.
【详解】由题意得sinA==,故选B.
【点睛】掌握正弦公式是解答本题的关键.
11.
【分析】根据折叠的性质结合勾股定理求得GE,BC=AD=8,证得Rt△EGFRt△EAG,求得,再利用勾股定理得到DE的长,即可求解.
【详解】矩形中,GC=4,CE =3,∠C=90,
∴GE=,
根据折叠的性质:BG=GF,GF=GC=4,CE=EF=3,∠AGB=∠AGF,∠EGC=∠EGF,∠GFE =∠C=90,
∴BG=GF=GC=4,
∴BC=AD=8,
∵∠AGB+∠AGF+∠EGC+∠EGF=180,
∴∠AGE=90,
∴Rt△EGFRt△EAG,
∴,即,
∴,
∴DE=,
∴,
故答案为:.
【点睛】本考查了折叠的性质,矩形的性质,勾股定理的应用,相似三角形的判定和性质,锐角三角形函数的知识等,利用勾股定理和相似三角形的性质求线段的长度是本题的关键.
12.3
【详解】试题解析:平移CD到C′D′交AB于O′,如图所示,
则∠BO′D′=∠BOD,
∴tan∠BOD=tan∠BO′D′,
设每个小正方形的边长为a,
则O′B=,O′D′=,BD′=3a,
作BE⊥O′D′于点E,
则BE=,
∴O′E=,
∴tanBO′E=,
∴tan∠BOD=3.
考点:解直角三角形.
13.
【分析】设AD=BC=x,可证△ABC∽△CBD,根据相似三角形的性质表示出BD的长,然后在△Rt△BCD中,利用余弦的定义求解即可.
【详解】设AD=BC=x,
∵∠ACB=90°,CD⊥AB,
∴∠A+∠ACD=∠ACD+∠BCD=90°,
∴∠A=∠BCD,
∴△ABC∽△CBD,
∴,即,
∴BD=x,
∴cos∠B==,
故答案为.
【点睛】本题考查了相似三角形的判定与性质,锐角三角函数的定义,由△ABC∽△CBD表示出BD的长是解答本题的关键.
14.233m
【分析】作AD⊥BC交CB的延长线于D,设AD为x,表示出DB和DC,根据正切的概念求出x的值即可.
【详解】解:作AD⊥BC交CB的延长线于D,设AD为x,
由题意得,∠ABD=45°,∠ACD=35°,
在Rt△ADB中,∠ABD=45°,
∴DB=x,
在Rt△ADC中,∠ACD=35°,
,
,
解得,x≈233.
所以,热气球离地面的高度约为233米.
故答案为:233.
【点睛】本题考查的是解直角三角形的应用,理解仰角和俯角的概念、掌握锐角三角函数的概念是解题的关键,解答时,注意正确作出辅助线构造直角三角形.
15.6
【分析】取AC的中点F,过F作于G,延长FG至E,使EG=FG,连接AE交BC于D,则 此时最短,证明此时D为BC的中点,证明CD=2DF,从而可得答案.
【详解】解:如图,
取AC的中点F,过F作于G,延长FG至E,使EG=FG,连接AE交BC于D,则 此时最短,
过A作于H,则由
为BC的中点,
即的最小值为6.
故答案为:6.
【点睛】本题考查的是利用轴对称求最小值问题,考查了锐角三角函数,三角形的相似的判定与性质,直角三角形的性质,勾股定理的应用,掌握以上知识是解题的关键.
16.(1)证明见解析(2)△AEG与△BHF相似 (3)
【详解】试题分析:(1)由于△ABD是等边三角形,那么∠D=∠EAG=60°,根据折叠的性质知:∠D=∠GCH=∠AEG=60°,再加上对顶角∠EGA=∠HGC,即可证得所求的三角形相似;
(2)由△ABD是等边三角形和的性质知:∠BAD=∠GCH=∠ABD,再由三角形内角和定理可证明∠1=∠5,即可得到结论;
(3)在Rt△ABC中,已知了BC的长和∠BAC的度数,即可求得AB、AC的值,由折叠的性质知:DE=CE,可设出DE、CE的长,然后表示出AE的长,进而可在Rt△AEC中,由勾股定理求得AE、CE的值,即可得到∠AEG的余弦值,而根据(1)的相似三角形知∠AEG=∠CHG,由此得解.
试题解析:解:(1)∵△ABD是等边三角形,∴∠EAG=∠D=60°;
根据折叠的性质知:DE=CE,∠D=∠GCH=∠EAG=60°,又∵∠EGA=∠HGC,∴△AEG∽△CHG.
(2)△AEG与△BHF相似.理由如下:
∵∠BAD=∠ABD=∠D,∠GCH=∠D,∴∠BAD=∠GCH=∠ABD,∴∠1+∠2=∠3+∠4.∵∠2=∠3,∠4=∠5,∴∠1=∠5, ∴△AEG∽△BHF;
(3)△ABC中,∠BAC=30°,BC=1,则AC=,AB=2,故AD=AB=2.
设DE=EC=x,则AE=2﹣x.
在Rt△AEC中,由勾股定理,得:(2﹣x)2+3=x2,解得x=,∴AE=,EC=,∴cos∠AEC==.由(1)的相似三角形知:∠AEG=∠CHG,故cos∠CHG=cos∠AEC=.
点睛:此题考查的知识点有:等边三角形的性质、相似三角形的判定和性质、图形的翻折变换以及锐角三角函数的定义等知识,难度适中.
17.这栋楼的高度约为95米.
【分析】利用正切函数分别在Rt△ABD与Rt△ACD中求得BD与CD的长即可.
【详解】由题意可知,,米,
在中,(米),
在中,(米),
(米).
答:这栋楼的高度约为95米.
【点睛】本题考查了解直角三角形的应用,准确确定直角三角形,灵活运用相关知识是解此题的关键.
18.(1)见解析1;(2)
【分析】(1)根据题意由平行四边形性质得,由ASA证得,即可得出结论;
(2)根据题意由(1)得OE=OF,则OE=2,在Rt△OEB中,由三角函数定义即可得出结果.
【详解】解:(1)证明:在中,
∵,
∴
∴
又∵
∴
∴
(2)∵,
∴
∵
∴
在中,,.
【点睛】本题考查平行四边形的性质、全等三角形的判定与性质、三角函数定义等知识;熟练掌握平行四边形的性质与全等三角形的判定是解题的关键.
19.(1)75°;(2)
【分析】(1)如图:过点A作于点E,在Rt△ABC中运用三角函数可得,即、进一步可得∠EAC=30°,再结合即可解答;
(2)先根据题意求得DE=AE=,然后在Rt△ACE中解直角三角形求得CE,最后利用CD=CE+DE进行计算即可.
【详解】(1)如图:过点A作于点E,
∵在Rt△ABC中,
∵AE//BC
;
(2)∵在RtAED中,AE=BC=,∠DAE=45°
∴DE=AE=
∵在Rt△ACE中,∠CAE=30°
∴CE=tan30°·AE=30
.
【点睛】本题主要考查了运用三角函数值求角的大小和解直角三角形,灵活应用三角函数知识是解答本题的关键.
20.沿海城市B会受到这次风暴的影响,受影响的时间为4小时
【分析】作出图像,求出风暴离B城市的最近距离BD= 30千米,判断出沿海城市B会受到这次风暴的影响,接下来计算受影响的时长,得沿海城市B受影响时风暴所走的路程为线段EF,求出EF的长,除以速度即可解题.
【详解】根据题意画出图形,
根据题意可知AB=60千米,∠BAF=30°
过B作BD⊥AF于点D,作BE=BF=50千米,分别交AF于点E、F
∵ BD⊥AF,AB=60千米,∠BAF=30°
∴ 风暴离B城市的最近距离为BD=AB×sin30°=30千米,
∵ BD<50千米
∴ 沿海城市B会受到这次风暴的影响
∵ BE=BF=50千米
∴ 沿海城市B受影响时风暴所走的路程为线段EF
∵ BE=BF=50千米,BD=30千米,BD⊥AF
∴ DF=DE=
∴ EF=2DF=80千米
∵ 风暴速度为每小时20千米
∴ 受影响时间==4小时
∴沿海城市B会受到这次风暴的影响,受影响的时间为4小时.
【点睛】本题主要考查了,含30°的特殊直角三角形的实际应用,中等难度,在理解题意的基础上求出BD与EF的长是解题关键.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
