【精选备课】2022-2023学年湘教版(2012)数学九年级上册 第五单元测试(含解析)
文档属性
| 名称 | 【精选备课】2022-2023学年湘教版(2012)数学九年级上册 第五单元测试(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 315.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-22 10:35:31 | ||
图片预览




文档简介
第五单元测试
一、单选题
1.某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如下表:
金额/元 5 10 20 50 100
人数 4 16 15 9 6
则他们捐款金额的中位数和平均数分别是( )A.10,20.6 B.20,20.6 C.10,30.6 D.20,30.6
2.一城市准备选购一千株高度大约为2m的某种风景树来进行街道绿化,有四个苗圃生产基地投标(单株树苗的价格都一样).采购小组从四个苗圃中都任意抽查了20株树苗的高度,得到的数据如下:请你帮采购小组出谋划策,应选购( )
A.甲苗圃的树苗 B.乙苗圃的树苗
C.丙苗圃的树苗 D.丁苗圃的树苗
3.某住宅小区4月份1日至6日每天用水量变化情况如图,那么4月份的总用水量约为( )吨(一个月按30天算)
A.900 B.930
C.960 D.990
4.某校对460名九年级学生进行跳绳技能培训,以提高同学们的跳绳成绩.为了解培训的效果,随机抽取了40名同学进行测试,测试结果分成“不合格”“合格”“良好”“优秀”四个等级,并绘制了如图所示的统计图,从图中可以估计出该校460名九年级学生中,能获得跳绳“优秀”的总人数大约是( )
A.10 B.16 C.115 D.150
5.为了鼓励学生课外阅读,学校公布了“阅读奖励”方案,并设置了“赞成、反对、无所谓”三种意见.现从学校所有2400名学生中随机征求了100名学生的意见,其中持“反对”和“无所谓”意见的共有30名学生,估计全校持“赞成”意见的学生人数约为( )
A.70 B.720 C.1680 D.2370
6.某专卖店专营某品牌的衬衫,店主对上一周中不同尺码的衬衫销售情况统计如下:
该店主决定本周进货时,增加了一些41码的衬衫,影响该店主决策的统计量是( )
A.平均数 B.方差 C.众数 D.中位数
7.在Rt△ABC中,∠C =90°,sinA=,则cosB的值等于( )
A. B. C. D.
8.某校对全体学生开展心理健康知识测试,七、八、九三个年级共有800名学生,各年级的合格人数如下表所示,则下列说法正确的是( )
年级 七年级 八年级 九年级
合格人数 270 262 254
A.七年级的合格率最高 B.八年级的学生人数为262名
C.八年级的合格率高于全校的合格率 D.九年级的合格人数最少
9.某排球队名场上队员的身高(单位:)是:,,,,,.现用一名身高为的队员换下场上身高为的队员,与换人前相比,场上队员的身高( )
A.平均数变小,方差变小 B.平均数变小,方差变大
C.平均数变大,方差变小 D.平均数变大,方差变大
10.从250个数据中用适当的方法抽取50个作为样本进行统计,在频数分布表中,落在90.5~100.5这一组的频率是0.12,那么估计总体数据在90.5~100.5之间的个数为( )
A.60个 B.30个 C.12个 D.6个
二、填空题
11.一个样本为1,3,2,2,a,b,c,已知这个样本的众数为3,平均数为2,则这组数据的中位数为______.
12.如图,某校根据学生上学方式的一次抽样调查结果,绘制出一个未完成的扇形统计图,若该校共有学生700人,则据此估计步行的有_____人.
13.小燕抛一枚硬币10次,有7次正面朝上,当她抛第11次时,正面向上的概率为_________.
14.第十二届全国人大四次会议审议通过的《中华人民共和国慈善法》将于今年9月1日正式实施,为了了解居民对慈善法的知晓情况,某街道办从辖区居民中随机选取了部分居民进行调查,并将调查结果绘制成如图所示的扇形图.若该辖区约有居民9000人,则可以估计其中对慈善法“非常清楚”的居民约有______人.
15.为了解某新品种黄瓜的生长情况,抽查了部分黄瓜株上长出的黄瓜根数,得到如图所示的条形统计图,观察改图,可知共抽查了________株黄瓜,并可估计出这个新品种黄瓜平均每株结________根黄瓜.
三、解答题
16.为了让同学们了解自己的体育水平,初二1班的体育刘老师对全班45名学生进行了一次体育模拟测试(得分均为整数),成绩满分为10分,1班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
初二1班体育模拟测试成绩分析表
平均分 方差 中位数 众数
男生 2 8 7
女生 7.92 1.99 8
根据以上信息,解答下列问题:
(1)这个班共有男生 人,共有女生 人;
(2)补全初二1班体育模拟测试成绩分析表.
17.如图,某数学活动小组为测量学校旗杆AB的高度,沿旗杆正前方米处的点C出发,沿斜面坡度的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈,cos37°≈,tan37°≈.计算结果保留根号)
18.松雷中学校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,下图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8:2,又知此次调查中捐15元和20元的人数共39人.
(1)他们一共抽查了多少人?
(2)若该校共有2310名学生,请估计全校学生共捐款多少元?
19.A,B,C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表和图1:
(1)请将表和图1中的空缺部分补充完整.
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图2(没有弃权票,每名学生只能推荐一个),则B在扇形统计图中所占的圆心角的度数是______.
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
20.某班同学上学期全部参加了捐款活动,捐款情况如下统计表:
金额(元) 5 10 15 20 25 30
人数(人) 8 12 10 6 2 2
(1)求该班学生捐款额的平均数和中位数;
(2)试问捐款额多于15元的学生数是全班人数的百分之几?
(3)已知这笔捐款是按3:5:4的比例分别捐给灾区民众、重病学生、孤老病者三种被资助的对象,问该班捐给重病学生是多少元?
参考答案:
1.D
【详解】试题分析:根据中位数的定义求解即可,中位数是将一组数据从小到大重新排列后,找出最中间两个数的平均数;可知共有50个数,且中位数是第25、26个数的平均数,可得中位数是(20+20)÷2=20;
平均数=(5×4+10×16+20×15+50×9+100×6)=30.6;
故选D.
考点:1、中位数;2、统计表;3、加权平均数
2.D
【详解】根据方差的意义:反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.再根据树苗的高度的平均数,选择丁苗圃的树苗.
解:根据表中数据可知甲、丁的方差小,波动小,树苗较整齐;
而甲树苗的高度为1.8m,丁树苗的高度为2.0m,根据题意选择丁苗圃的树苗.
故选D.
3.C
【分析】根据函数图象得到每天的用水量,根据算术平均数的计算公式计算即可.
【详解】这6天的平均用水量==32(吨).故4月份的总用水量约为=32×30=960(吨).
故选C.
【点睛】本题考查的是函数的图象和算术平均数的计算,读懂图象信息、掌握平均数的计算公式是解题的关键.
4.C
【详解】【分析】用样本的优秀率估计总体的优秀率.
【详解】从图中可以估计出该校460名九年级学生中,能获得跳绳“优秀”的总人数大约是460×=115(人)
故选C
【点睛】本题考核知识点:用样本估计总体. 解题关键点:求样本的优秀率.
5.C
【详解】解:,
故答案选C.
6.C
【分析】用到的知识点:一组数据中出现次数最多的数据叫做这组数据的众数.将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.平均数是指在一组数据中所有数据之和再除以数据的个数.一般地设n个数据,x1,x2,…xn的平均数为,则方差S2= [(x1﹣)2+(x2﹣)2+…+(xn﹣)2].
【详解】解:41码共20件,最多,41码是众数,
故选C
考点:方差;加权平均数;中位数;众数
7.B
【详解】解:在Rt△ABC中,∠C=90°,sinA=,
则cosB=.
故选:B.
【点睛】本题考查了互余两角三角函数的关系.熟练运用三角函数的定义进行求解是解题关键.
8.D
【详解】解:∵七、八、九年级的人数不确定,∴无法求得七、八、九年级的合格率,∴A错误、C错误.
由统计表可知八年级合格人数是262人,故B错误.
∵270>262>254,∴九年级合格人数最少.
故D正确.故选D.
9.A
【详解】分析:根据平均数的计算公式进行计算即可,根据方差公式先分别计算出甲和乙的方差,再根据方差的意义即可得出答案.
详解:换人前6名队员身高的平均数为==188,
方差为S2==;
换人后6名队员身高的平均数为==187,
方差为S2==
∵188>187,>,
∴平均数变小,方差变小,
故选A.
点睛:本题考查了平均数与方差的定义:一般地设n个数据,x1,x2,…xn的平均数为,则方差S2=[(x1-)2+(x2-)2+…+(xn-)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
10.B
【分析】用样本的频率估计总体的频率,再乘以总数.
【详解】解:因为样本中落在90.5~100.5这一组的频率是0.12,
所以,可估计总体数据在90.5~100.5之间的频率是0.12,
人数大约250×0.12=30(个)
故选B
11.2.
【详解】解:因为众数为3,可设a=3,b=3,c未知,平均数=(1+3+2+2+3+3+c)÷7=2,解得c=0,将这组数据按从小到大的顺序排列:0、1、2、2、3、3、3,位于最中间的一个数是2,所以中位数是2,故答案为2.
点睛:本题为统计题,考查平均数、众数与中位数的意义,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.
12.280
【分析】根据扇形统计图可得该校学生骑车上学的人数占总人数的百分比是,然后用总体乘骑车上学的百分比即可.
【详解】解:根据扇形统计图可得:该校学生骑车上学的人数占总人数的百分比是,
∴估计该校学生上学步行的人数=700×(1-10%-15%-35%)=280人.
【点睛】考点:1.扇形统计图;2.样本估计总体.
13.
【分析】求出一次抛一枚硬币正面朝上的概率即可.
【详解】解:∵抛硬币正反出现的概率是相同的,不论抛多少次出现正面或反面的概率是一致的,
∴正面向上的概率为.
故答案为.
【点睛】本题考查的是概率的公式,注意抛硬币只有两种情况,每次抛出的概率都是一致的,与次数无关.
14.2700
【分析】先求出“非常清楚”所占的百分比,再乘以该辖区的总居民数,即可得出答案.
【详解】解:根据题意得:9000×(1 30% 15% ×100%)
=9000×30%
=2700(人),
答:可以估计其中对慈善法“非常清楚”的居民约有2700人,
故答案为:2700.
【点睛】本题考查根据扇形统计图信息求某项目的数据,熟练掌握在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比是解决问题的关键.
15. 60 13
【详解】试题解析:
共抽查:15+10+15+20=60(株),
平均数是:(15×10+10×12+15×14+20×15)÷60=13.
故答案为60,13.
点睛:根据平均数的定义进行计算即可.
16. 20 25
【详解】试题分析:(1)由条形图可得男生总人数,总人数减去男生人数可得女生人数;
(2)根据平均数和众数定义可得.
试题解析:解:(1)这个班共有男生1+2+6+3+5+3=20人,共有女生45﹣20=25人,故答案为20、25;
(2)甲的平均分为×(5+6×2+7×6+8×3+9×5+10×3)=7.9,女生的众数为8,补全表格如下:
点睛:本题主要考查平均数、众数及条形图、扇形图,根据统计图得出解题所需数据,并熟练掌握平均数和众数的定义是解题的关键.
17.3+3.5
【分析】延长ED交BC延长线于点F,则∠CFD=90°,Rt△CDF中求得CF=CDcos∠DCF=2、DF=CD=2,作EG⊥AB,可得GE=BF=4、GB=EF=3.5,再求出AG=GEtan∠AEG=4 tan37°可得答案.
【详解】如图,延长ED交BC延长线于点F,则∠CFD=90°,
∵tan∠DCF=i=,
∴∠DCF=30°,
∵CD=4,
∴DF=CD=2,CF=CDcos∠DCF=4×=2,
∴BF=BC+CF=2+2=4,
过点E作EG⊥AB于点G,
则GE=BF=4,GB=EF=ED+DF=1.5+2=3.5,
又∵∠AED=37°,
∴AG=GEtan∠AEG=4 tan37°,
则AB=AG+BG=4 tan37°+3.5=3+3.5,
故旗杆AB的高度为(3+3.5)米.
考点:1、解直角三角形的应用﹣仰角俯角问题;2、解直角三角形的应用﹣坡度坡角问题
18.(1)66;(2)36750.
【分析】(1)由条形统计图可得抽查的总人数,
(2)先求出这组数据的平均数,用平均数乘以总人数即可求出捐款总数.
【详解】解:(1)设捐15元的人数为5x,则根据题意捐20元的人数为8x.
则5x+8x=39,解得:x=3
则一共调查了3x+4x+5x+8x+2x=66(人);
(2)全校学生共捐款:
(9×5+12×10+15×15+24×20+6×30)÷66×2310=36750(元).
【点睛】本题考查了条形统计图的实际应用,属于简单题,从统计图中得到有用信息是解题关键.
19.(1)答案见解析;(2)144°;(3)B当选.
【分析】(1)见下表,
(2)360°乘以B占的比重即可解题,
(3)根据加权平均数的计算方法即可解题,
【详解】解:(1)补充图形如下:
;
(2)360°×40%=144°;
(3)A的投票得分是:300×35%=105(分),则A的最后得分是:=92(分);
B的投票得到是:300×40%=120(分),则B的最后得分是:=98(分);
C的投票得分是:300×25%=75(分),则C的最终得分是:=84(分).
所以B当选.
【点睛】本题考查了条形统计图和扇形统计图的综合应用,加权平均数的计算,综合性较强,中等难度,从不同统计图中得到有用信息是解题关键.
20.(1)捐款平均数为13.5元;中位数为12.5元;(2)捐款额多于15元的学生数是全班人数的25%;(3)重病学生可以得到225元的救助.
【分析】(1)根据平均数和中位数公式即可求解,
(2)找到捐款多于15元的人数,与总人数相比即可,
(3)找到重病学生在三种资助对象中的占比即可解题.
【详解】(1)捐款平均数为
=13.5元;
∵共40人,
∴中位数应该是第20和第21人的平均数,
∵第20人捐款10元,第21人捐款15元,
∴中位数为12.5元;
(2)捐款多于15元的有6+2+2=10人,
故10÷40×100%=25%;
(3)∵捐款共计540元,按照3:5:4的比例分配给灾区民众、重病学生、孤老病者三种被资助的对象,
∴重病学生可以得到540×=225元的救助.
【点睛】本题考查了条形统计图的实际应用,属于简单题,熟记公式是解题关键.
一、单选题
1.某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如下表:
金额/元 5 10 20 50 100
人数 4 16 15 9 6
则他们捐款金额的中位数和平均数分别是( )A.10,20.6 B.20,20.6 C.10,30.6 D.20,30.6
2.一城市准备选购一千株高度大约为2m的某种风景树来进行街道绿化,有四个苗圃生产基地投标(单株树苗的价格都一样).采购小组从四个苗圃中都任意抽查了20株树苗的高度,得到的数据如下:请你帮采购小组出谋划策,应选购( )
A.甲苗圃的树苗 B.乙苗圃的树苗
C.丙苗圃的树苗 D.丁苗圃的树苗
3.某住宅小区4月份1日至6日每天用水量变化情况如图,那么4月份的总用水量约为( )吨(一个月按30天算)
A.900 B.930
C.960 D.990
4.某校对460名九年级学生进行跳绳技能培训,以提高同学们的跳绳成绩.为了解培训的效果,随机抽取了40名同学进行测试,测试结果分成“不合格”“合格”“良好”“优秀”四个等级,并绘制了如图所示的统计图,从图中可以估计出该校460名九年级学生中,能获得跳绳“优秀”的总人数大约是( )
A.10 B.16 C.115 D.150
5.为了鼓励学生课外阅读,学校公布了“阅读奖励”方案,并设置了“赞成、反对、无所谓”三种意见.现从学校所有2400名学生中随机征求了100名学生的意见,其中持“反对”和“无所谓”意见的共有30名学生,估计全校持“赞成”意见的学生人数约为( )
A.70 B.720 C.1680 D.2370
6.某专卖店专营某品牌的衬衫,店主对上一周中不同尺码的衬衫销售情况统计如下:
该店主决定本周进货时,增加了一些41码的衬衫,影响该店主决策的统计量是( )
A.平均数 B.方差 C.众数 D.中位数
7.在Rt△ABC中,∠C =90°,sinA=,则cosB的值等于( )
A. B. C. D.
8.某校对全体学生开展心理健康知识测试,七、八、九三个年级共有800名学生,各年级的合格人数如下表所示,则下列说法正确的是( )
年级 七年级 八年级 九年级
合格人数 270 262 254
A.七年级的合格率最高 B.八年级的学生人数为262名
C.八年级的合格率高于全校的合格率 D.九年级的合格人数最少
9.某排球队名场上队员的身高(单位:)是:,,,,,.现用一名身高为的队员换下场上身高为的队员,与换人前相比,场上队员的身高( )
A.平均数变小,方差变小 B.平均数变小,方差变大
C.平均数变大,方差变小 D.平均数变大,方差变大
10.从250个数据中用适当的方法抽取50个作为样本进行统计,在频数分布表中,落在90.5~100.5这一组的频率是0.12,那么估计总体数据在90.5~100.5之间的个数为( )
A.60个 B.30个 C.12个 D.6个
二、填空题
11.一个样本为1,3,2,2,a,b,c,已知这个样本的众数为3,平均数为2,则这组数据的中位数为______.
12.如图,某校根据学生上学方式的一次抽样调查结果,绘制出一个未完成的扇形统计图,若该校共有学生700人,则据此估计步行的有_____人.
13.小燕抛一枚硬币10次,有7次正面朝上,当她抛第11次时,正面向上的概率为_________.
14.第十二届全国人大四次会议审议通过的《中华人民共和国慈善法》将于今年9月1日正式实施,为了了解居民对慈善法的知晓情况,某街道办从辖区居民中随机选取了部分居民进行调查,并将调查结果绘制成如图所示的扇形图.若该辖区约有居民9000人,则可以估计其中对慈善法“非常清楚”的居民约有______人.
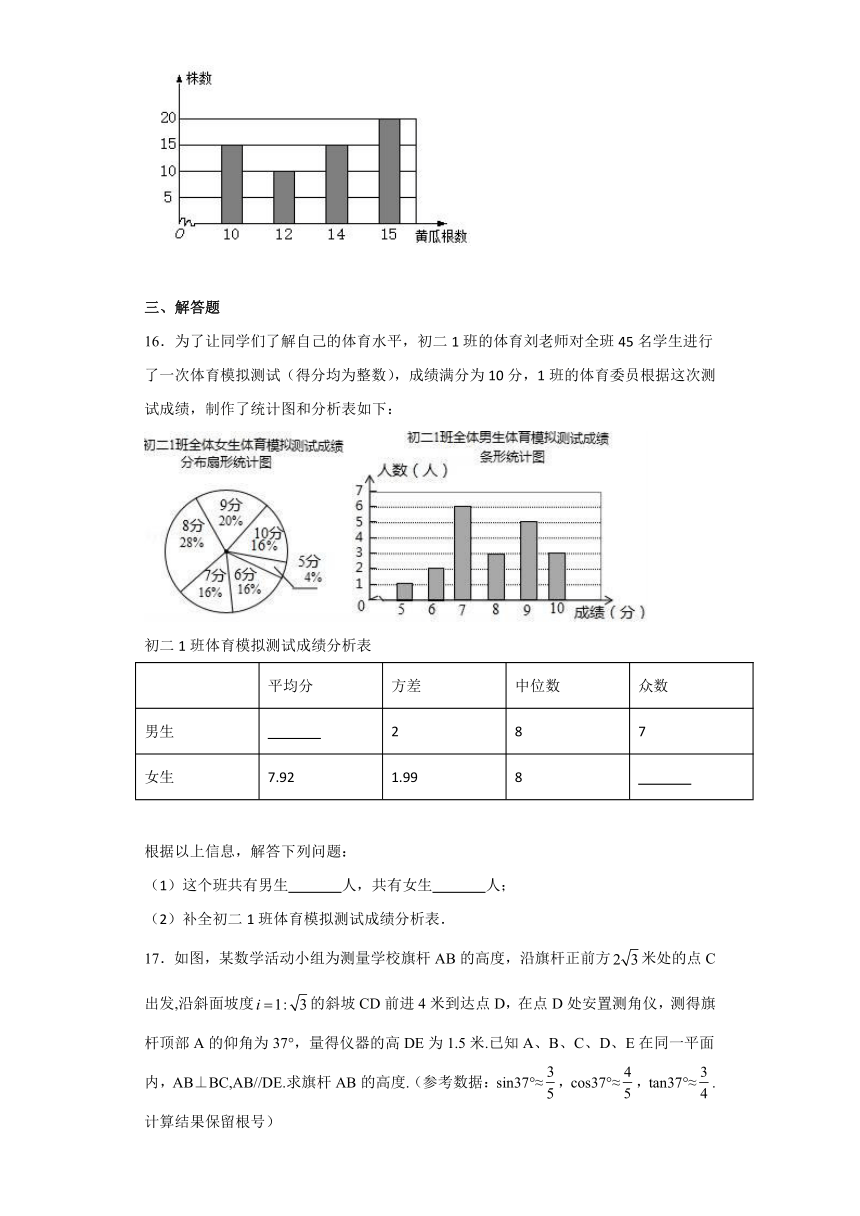
15.为了解某新品种黄瓜的生长情况,抽查了部分黄瓜株上长出的黄瓜根数,得到如图所示的条形统计图,观察改图,可知共抽查了________株黄瓜,并可估计出这个新品种黄瓜平均每株结________根黄瓜.
三、解答题
16.为了让同学们了解自己的体育水平,初二1班的体育刘老师对全班45名学生进行了一次体育模拟测试(得分均为整数),成绩满分为10分,1班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
初二1班体育模拟测试成绩分析表
平均分 方差 中位数 众数
男生 2 8 7
女生 7.92 1.99 8
根据以上信息,解答下列问题:
(1)这个班共有男生 人,共有女生 人;
(2)补全初二1班体育模拟测试成绩分析表.
17.如图,某数学活动小组为测量学校旗杆AB的高度,沿旗杆正前方米处的点C出发,沿斜面坡度的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈,cos37°≈,tan37°≈.计算结果保留根号)
18.松雷中学校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,下图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8:2,又知此次调查中捐15元和20元的人数共39人.
(1)他们一共抽查了多少人?
(2)若该校共有2310名学生,请估计全校学生共捐款多少元?
19.A,B,C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表和图1:
(1)请将表和图1中的空缺部分补充完整.
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图2(没有弃权票,每名学生只能推荐一个),则B在扇形统计图中所占的圆心角的度数是______.
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
20.某班同学上学期全部参加了捐款活动,捐款情况如下统计表:
金额(元) 5 10 15 20 25 30
人数(人) 8 12 10 6 2 2
(1)求该班学生捐款额的平均数和中位数;
(2)试问捐款额多于15元的学生数是全班人数的百分之几?
(3)已知这笔捐款是按3:5:4的比例分别捐给灾区民众、重病学生、孤老病者三种被资助的对象,问该班捐给重病学生是多少元?
参考答案:
1.D
【详解】试题分析:根据中位数的定义求解即可,中位数是将一组数据从小到大重新排列后,找出最中间两个数的平均数;可知共有50个数,且中位数是第25、26个数的平均数,可得中位数是(20+20)÷2=20;
平均数=(5×4+10×16+20×15+50×9+100×6)=30.6;
故选D.
考点:1、中位数;2、统计表;3、加权平均数
2.D
【详解】根据方差的意义:反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.再根据树苗的高度的平均数,选择丁苗圃的树苗.
解:根据表中数据可知甲、丁的方差小,波动小,树苗较整齐;
而甲树苗的高度为1.8m,丁树苗的高度为2.0m,根据题意选择丁苗圃的树苗.
故选D.
3.C
【分析】根据函数图象得到每天的用水量,根据算术平均数的计算公式计算即可.
【详解】这6天的平均用水量==32(吨).故4月份的总用水量约为=32×30=960(吨).
故选C.
【点睛】本题考查的是函数的图象和算术平均数的计算,读懂图象信息、掌握平均数的计算公式是解题的关键.
4.C
【详解】【分析】用样本的优秀率估计总体的优秀率.
【详解】从图中可以估计出该校460名九年级学生中,能获得跳绳“优秀”的总人数大约是460×=115(人)
故选C
【点睛】本题考核知识点:用样本估计总体. 解题关键点:求样本的优秀率.
5.C
【详解】解:,
故答案选C.
6.C
【分析】用到的知识点:一组数据中出现次数最多的数据叫做这组数据的众数.将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.平均数是指在一组数据中所有数据之和再除以数据的个数.一般地设n个数据,x1,x2,…xn的平均数为,则方差S2= [(x1﹣)2+(x2﹣)2+…+(xn﹣)2].
【详解】解:41码共20件,最多,41码是众数,
故选C
考点:方差;加权平均数;中位数;众数
7.B
【详解】解:在Rt△ABC中,∠C=90°,sinA=,
则cosB=.
故选:B.
【点睛】本题考查了互余两角三角函数的关系.熟练运用三角函数的定义进行求解是解题关键.
8.D
【详解】解:∵七、八、九年级的人数不确定,∴无法求得七、八、九年级的合格率,∴A错误、C错误.
由统计表可知八年级合格人数是262人,故B错误.
∵270>262>254,∴九年级合格人数最少.
故D正确.故选D.
9.A
【详解】分析:根据平均数的计算公式进行计算即可,根据方差公式先分别计算出甲和乙的方差,再根据方差的意义即可得出答案.
详解:换人前6名队员身高的平均数为==188,
方差为S2==;
换人后6名队员身高的平均数为==187,
方差为S2==
∵188>187,>,
∴平均数变小,方差变小,
故选A.
点睛:本题考查了平均数与方差的定义:一般地设n个数据,x1,x2,…xn的平均数为,则方差S2=[(x1-)2+(x2-)2+…+(xn-)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
10.B
【分析】用样本的频率估计总体的频率,再乘以总数.
【详解】解:因为样本中落在90.5~100.5这一组的频率是0.12,
所以,可估计总体数据在90.5~100.5之间的频率是0.12,
人数大约250×0.12=30(个)
故选B
11.2.
【详解】解:因为众数为3,可设a=3,b=3,c未知,平均数=(1+3+2+2+3+3+c)÷7=2,解得c=0,将这组数据按从小到大的顺序排列:0、1、2、2、3、3、3,位于最中间的一个数是2,所以中位数是2,故答案为2.
点睛:本题为统计题,考查平均数、众数与中位数的意义,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.
12.280
【分析】根据扇形统计图可得该校学生骑车上学的人数占总人数的百分比是,然后用总体乘骑车上学的百分比即可.
【详解】解:根据扇形统计图可得:该校学生骑车上学的人数占总人数的百分比是,
∴估计该校学生上学步行的人数=700×(1-10%-15%-35%)=280人.
【点睛】考点:1.扇形统计图;2.样本估计总体.
13.
【分析】求出一次抛一枚硬币正面朝上的概率即可.
【详解】解:∵抛硬币正反出现的概率是相同的,不论抛多少次出现正面或反面的概率是一致的,
∴正面向上的概率为.
故答案为.
【点睛】本题考查的是概率的公式,注意抛硬币只有两种情况,每次抛出的概率都是一致的,与次数无关.
14.2700
【分析】先求出“非常清楚”所占的百分比,再乘以该辖区的总居民数,即可得出答案.
【详解】解:根据题意得:9000×(1 30% 15% ×100%)
=9000×30%
=2700(人),
答:可以估计其中对慈善法“非常清楚”的居民约有2700人,
故答案为:2700.
【点睛】本题考查根据扇形统计图信息求某项目的数据,熟练掌握在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比是解决问题的关键.
15. 60 13
【详解】试题解析:
共抽查:15+10+15+20=60(株),
平均数是:(15×10+10×12+15×14+20×15)÷60=13.
故答案为60,13.
点睛:根据平均数的定义进行计算即可.
16. 20 25
【详解】试题分析:(1)由条形图可得男生总人数,总人数减去男生人数可得女生人数;
(2)根据平均数和众数定义可得.
试题解析:解:(1)这个班共有男生1+2+6+3+5+3=20人,共有女生45﹣20=25人,故答案为20、25;
(2)甲的平均分为×(5+6×2+7×6+8×3+9×5+10×3)=7.9,女生的众数为8,补全表格如下:
点睛:本题主要考查平均数、众数及条形图、扇形图,根据统计图得出解题所需数据,并熟练掌握平均数和众数的定义是解题的关键.
17.3+3.5
【分析】延长ED交BC延长线于点F,则∠CFD=90°,Rt△CDF中求得CF=CDcos∠DCF=2、DF=CD=2,作EG⊥AB,可得GE=BF=4、GB=EF=3.5,再求出AG=GEtan∠AEG=4 tan37°可得答案.
【详解】如图,延长ED交BC延长线于点F,则∠CFD=90°,
∵tan∠DCF=i=,
∴∠DCF=30°,
∵CD=4,
∴DF=CD=2,CF=CDcos∠DCF=4×=2,
∴BF=BC+CF=2+2=4,
过点E作EG⊥AB于点G,
则GE=BF=4,GB=EF=ED+DF=1.5+2=3.5,
又∵∠AED=37°,
∴AG=GEtan∠AEG=4 tan37°,
则AB=AG+BG=4 tan37°+3.5=3+3.5,
故旗杆AB的高度为(3+3.5)米.
考点:1、解直角三角形的应用﹣仰角俯角问题;2、解直角三角形的应用﹣坡度坡角问题
18.(1)66;(2)36750.
【分析】(1)由条形统计图可得抽查的总人数,
(2)先求出这组数据的平均数,用平均数乘以总人数即可求出捐款总数.
【详解】解:(1)设捐15元的人数为5x,则根据题意捐20元的人数为8x.
则5x+8x=39,解得:x=3
则一共调查了3x+4x+5x+8x+2x=66(人);
(2)全校学生共捐款:
(9×5+12×10+15×15+24×20+6×30)÷66×2310=36750(元).
【点睛】本题考查了条形统计图的实际应用,属于简单题,从统计图中得到有用信息是解题关键.
19.(1)答案见解析;(2)144°;(3)B当选.
【分析】(1)见下表,
(2)360°乘以B占的比重即可解题,
(3)根据加权平均数的计算方法即可解题,
【详解】解:(1)补充图形如下:
;
(2)360°×40%=144°;
(3)A的投票得分是:300×35%=105(分),则A的最后得分是:=92(分);
B的投票得到是:300×40%=120(分),则B的最后得分是:=98(分);
C的投票得分是:300×25%=75(分),则C的最终得分是:=84(分).
所以B当选.
【点睛】本题考查了条形统计图和扇形统计图的综合应用,加权平均数的计算,综合性较强,中等难度,从不同统计图中得到有用信息是解题关键.
20.(1)捐款平均数为13.5元;中位数为12.5元;(2)捐款额多于15元的学生数是全班人数的25%;(3)重病学生可以得到225元的救助.
【分析】(1)根据平均数和中位数公式即可求解,
(2)找到捐款多于15元的人数,与总人数相比即可,
(3)找到重病学生在三种资助对象中的占比即可解题.
【详解】(1)捐款平均数为
=13.5元;
∵共40人,
∴中位数应该是第20和第21人的平均数,
∵第20人捐款10元,第21人捐款15元,
∴中位数为12.5元;
(2)捐款多于15元的有6+2+2=10人,
故10÷40×100%=25%;
(3)∵捐款共计540元,按照3:5:4的比例分配给灾区民众、重病学生、孤老病者三种被资助的对象,
∴重病学生可以得到540×=225元的救助.
【点睛】本题考查了条形统计图的实际应用,属于简单题,熟记公式是解题关键.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
